Simulations

Introduction

While PR2-2015 simulations (FFP8) were focused on the reproduction of the flight data Gaussian noise power spectra and their time variations, this new PR3-2018 simulation (FFP10) brings for the first time the realistic simulation of instrumental effects for both HFI and LFI. Moreover these simulated systematic effects are processed in the timelines with the same algorithms (and when possible, codes) as for the flight data.

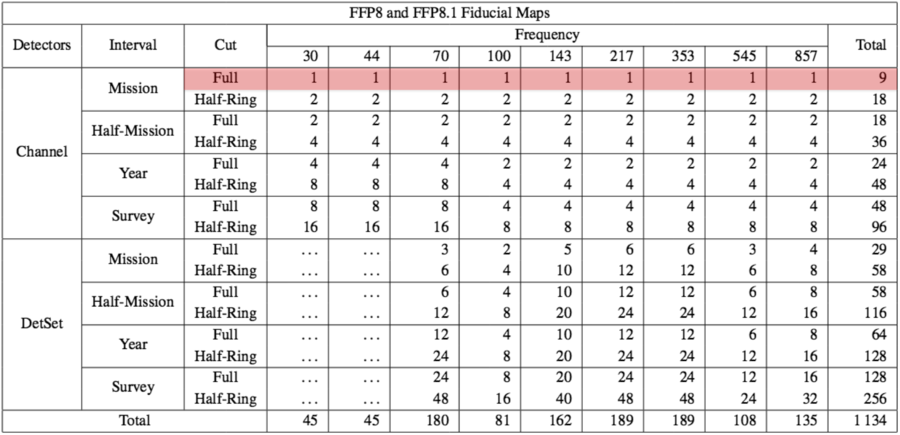
The FFP10 dataset is made of several full-sky map sets in FITS format:

• 1000 realizations of lensed scalar CMB convolved with effective beams per HFI frequency,
• separated input sky components per HFI bolometer and LFI radiometer
• 300 realizations of noise and systematic effect residuals per frequency,
• one fiducial simulation with full sky signal components: lensed scalar CMB, foregrounds, noise and systematic effect residuals, for all frequencies,

The end-to-end simulation pipeline

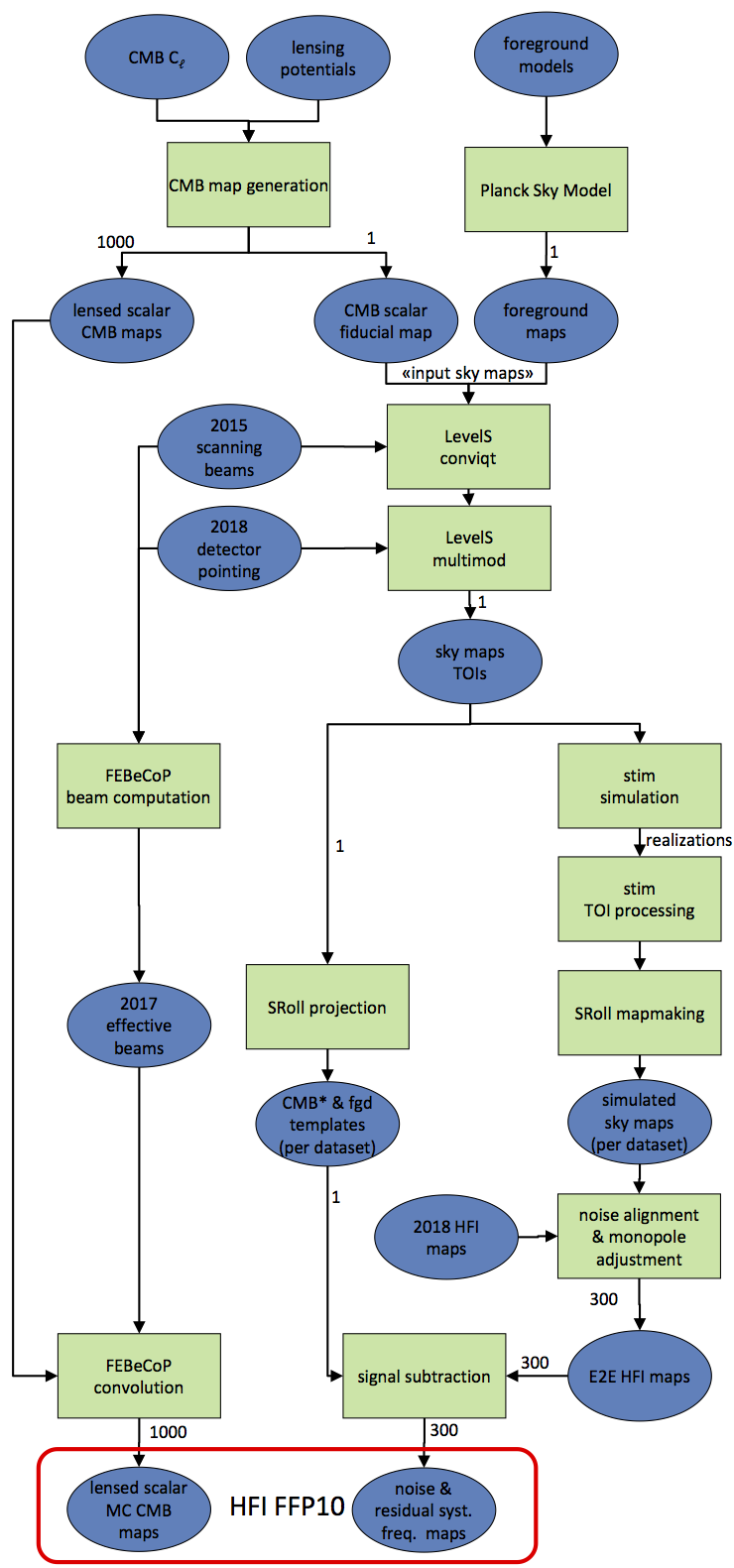
The end-to-end simulation pipeline uses several software components which are described below in the order they are used, as seen in the following schematic. Note that while this schematic is specific to HFI, the main components in the block diagram are similar for both instruments.

Please note that most of what is written here comes from Planck-2020-A3, which reading is highly recommended for more precisions on technical details and plots, particularly about the characterization of the negligible effects and systematics.

CMB

The FFP10 lensed CMB maps are generated in the same way as for the previous FFP8 release and described in detail in Planck-2015-A12. FFP10 simulations only contain the scalar part lensed with independent lensing potential realizations.

One "fiducial" realization is used as input CMB for the full end-to-end pipeline, and 1000 other realizations are convolved with FEBeCoP effective beams to be combined with the 300 noise and systematic residuals maps.

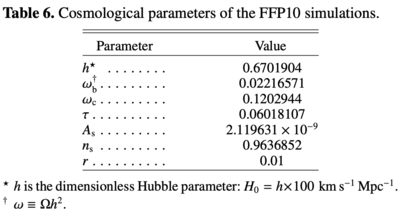
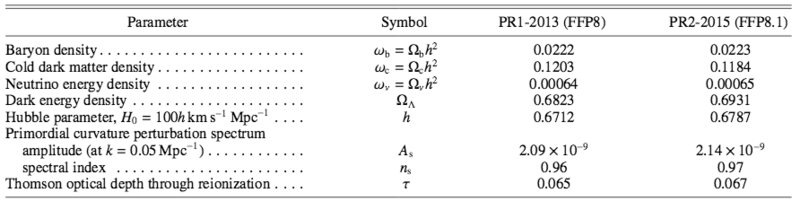
The cosmological parameters used are:

Parameter	Symbol	FFP8.1	FFP10
Baryon density	[math]\omega_b=\Omega_bh^2[/math]	[math]0.0223[/math]	[math]0.02216571[/math]
Cold dark matter density	[math]\omega_c=\Omega_ch^2[/math]	[math]0.1184[/math]	[math]0.1202944[/math]
Neutrino energy density	[math]\omega_{\nu}=\Omega_{\nu}h^2[/math]	[math]0.00065[/math]	[math]0.0006451439[/math]
Hubble parameter, [math]H_0=100h \mbox{ kms}^{-1} \mbox{ Mpc}^{-1}[/math]	[math]h[/math]	[math]0.6712[/math]	[math]0.6701904[/math]
Thomson optical depth through reionization	[math]\tau[/math]	[math]0.067[/math]	[math]0.06018107[/math]
Primordial curvature perturbation spectrum:
amplitude	[math]A_s[/math]	[math]2.14×10^{-9}[/math]	[math]2.119631×10^{-9}[/math]
spectral index	[math]n_s[/math]	[math]0.97[/math]	[math]0.9636852[/math]

The Planck Sky Model

The FFP10 simulation input sky is the coaddition of the following sky components generated using the Planck Sky Model (PSM) package (Delabrouille et al. 2013 ). Each of these components is convovled with each HFI bolometer spectral response by the PSM software, using the same spectral responses as in 2015 FFP8. Please note that one important difference with FFP8 is that FFP10 PSM maps are not smoothed with any beam, while in FFP8 PSM maps were smoothed with a 5’ Gaussian beam.

Diffuse Galactic components

• Dust

The dust model maps are built as follows. The Stokes I map at 353 GHz is the dust total intensity Planck map obtained by applying the Generalized Needlet Internal Linear Combination (GNILC) method of Remazeilles et al. (2011) to the PR2-2015 release of Planck HFI maps, as described in Planck-2016-XLVIII, and subtracting the monopole of the Cosmic Infrared Background (Planck-2015-A08). For the Stokes Q and U maps at 353 GHz, we started with one realization of the statistical model of Vansyngel et al. (2017). The portions of the simulated Stokes Q and U maps near Galactic plane were replaced by the Planck 353-GHz PR2 data. The transition between data and simulation was made using a Galactic mask with a 5° apodization, which leaves 68% of the sky unmasked at high latitude. Furthermore, on the full sky, the large angular scales in the simulated Stokes Q and U maps were replaced by the Planck data. Specifically, the first ten multipoles came from the Planck 353-GHz PR2 data, while over the [math]\ell=10-20[/math] range, the simulations were introduced smoothly using the function [math](1+{\sin}[\pi(15-\ell)/10])/2[/math].

To scale the dust Stokes maps from the 353-GHz templates to other Planck frequencies, we follow the FFP8 prescription (Planck-2015-A12). A different modified blackbody emission law is used for each of the [math]N_{side}=2048[/math] HEALPix pixels. The dust spectral index used for scaling in frequency is different for frequencies above and below 353 GHz. For frequencies above 353 GHz, the parameters come from the modified blackbody fit of the dust spectral energy distribution (SED) for total intensity obtained by applying the GNILC method to the PR2 HFI maps (Planck-2016-XLVIII). These parameter maps have a variable angular resolution that decreases towards high Galactic latitudes. Below 353 GHz, we also use the dust temperature map from Planck-2016-XLVIII, but with a distinct map of spectral indices from Planck-2013-XI, which has an angular resolution of 30’. These maps introduce significant spectral variations over the sky at high Galactic latitudes, and between the dust SEDs for total intensity and polarization. The spatial variations of the dust SED for polarization in the FFP10 sky model are quantified in [ttps://www.aanda.org/articles/aa/abs/2018/11/aa32888-18/aa32888-18.html#page=1 Planck-2018-LIV].

• Synchrotron

Synchrotron intensity is modelled by scaling in frequency the 408-MHz template map from Haslam et al. (1982), as reprocessed by Remazeilles et al. (2015) using a single power law per pixel. The pixel-dependent spectral index is derived from an analysis of WMAP data by Miville-Deschênes et al. (2008). The generation of synchrotron polarization follows the prescription of Delabrouille et al. (2013).

• Other components

Free-free, spinning dust models, and Galactic CO emissions are essentially the same as those used for the FFP8 sky model (Planck-2015-A12), but the actual synchrotron and free-free maps used for FFP10 are obtained with a different realization of small-scale fluctuations of the intensity. CO maps do not include small-scale fluctuations, and are generated from the spectroscopic survey of Dame et al. (2001). None of these three components is polarized in the FFP10 simulations.

Unresolved point sources and cosmic infrared background

Catalogues of individual radio and low-redshift infrared sources are generated in the same way as for FFP8 simulations (Planck-2015-A12), but use a different seed for random number generation. Number counts for three types of galaxies (early-type proto-spheroids, and more recent spiral and starburst galaxies) are based on the model of Cai et al. (2013). The entire Hubble volume out to redshift [math]z=6[/math] is cut into 64 spherical shells, and for each shell we generate a map of density contrast integrated along the line of sight between [math]z_{min}[/math] and [math]z_{max}[/math], such that the statistics of these density contrast maps (i.e., power spectrum of linear density fluctuations, and cross-spectra between adjacent shells, as well as with the CMB lensing potential), obey statistics computed using the Cosmic Linear Anisotropy Solving System (CLASS) code (Blas et al. 2011; Di Dio et al. 2013). For each type of galaxy, a catalogue of randomly-generated galaxies is generated for each shell, following the appropriate number counts. These galaxies are then distributed in the shell to generate a single intensity map at a given reference frequency, which is scaled across frequencies using the prototype galaxy SED at the appropriate redshift.

Galaxy clusters

A full-sky catalogue of galaxy clusters is generated based on number counts following the method of Delabrouille et al. (2002). The mass function of Tinker et al. (2008) is used to predict number counts. Clusters are distributed in redshift shells, proportionally to the density contrast in each pixel with a bias [math]b(z, M)[/math], in agreement with the linear bias model of Mo & White (1996). For each cluster, we assign a universal profile based on XMM observations, as described in Arnaud et al. (2010). Relativistic corrections are included to first order following the expansion of Nozawa et al. (1998). To assign an SZ flux to each cluster, we use a mass bias of [math]M_{Xray}/M_{true}=0.63[/math] to match actual cluster number counts observed by Planck for the best-fit cosmological model coming from CMB observations. We use the specific value [math]\sigma_8=0.8159[/math].

The kinematic SZ effect is computed by assigning to each cluster a radial velocity that is randomly drawn from a centred Gaussian distribution, with a redshift-dependent standard deviation that is computed from the power spectrum of density fluctuations. This neglects correlations between cluster motions, such as bulk flows or pairwise velocities of nearby clusters.

Input sky maps to timelines

The LevelS software package (Reinecke et al. 2006 ) is used to convert the input sky maps to timelines for each bolometer.

• Using conviqtv3, the maps are convolved with the same scanning beams as for FFP8, which were produced by stacking intensity-only observations of planets (Planck-2015-A07, appendix B), and to which a fake polarization has been added using a simple model based on each bolometer polarization angle and leakage.

• The convolved maps are then scanned to timelines with multimod, using the same scanning strategy as the 2018 flight data release. The only difference between the 2018 scanning strategy and the 2015 one is that about 1000 stable pointing periods at the end of the mission are omitted in 2018, because it has been found that the data quality was significantly lower in this interval.

Instrument-specific simulations

The main new aspect of FFP10 is the production of End-to-end (E2E) detector simulations, which include all significant systematic effects, and are used to produce realistic maps of noise and systematic effect residuals.

HFI E2E simulations

The pipeline adds the modelled instrumental systematic effects at the timeline level. It includes noise only up to the time response convolution step, after which the signal is added and the systematics simulated. It was shown in appendix B.3.1 of Planck-2016-XLVI that, including the CMB map in the inputs or adding it after mapmaking, leads to differences for the power spectra in CMB channels below the [math]10^{-4}\mu{K}^2[/math] level. This justifies the use of CMB swapping even when non-Gaussian systematic effects dominate over the TOI detector noise.

Here are the main effects included in the FFP10 simulation:

• White noise: the noise is based on a physical model composed of photon, phonon, and electronic noises. The time-transfer functions are different for these three noise sources. A timeline of noise only is created, with the level adjusted to agree with the observed TOI white noise after removal of the sky signal averaged per ring.

• Bolometer signal time-response convolution: the photon white noise is convolved with the bolometer time response using the same code and same parameters as in the 2015 processing. A second white noise contribution is added to the convolved photon white noise to simulate the electronics noise.

• Noise auto-correlation due to deglitching: the deglitching step in the data processing creates noise auto-correlation by flagging samples that are synchronous with the sky. Since we do not simulate the cosmic-ray glitches, we mimic this behaviour by adjusting the noise of samples above a given threshold to simulate their flagging.

• Time response deconvolution: the timeline containing the photon and electronic noise contributions is then deconvolved with the bolometer time response and low-pass filtered to limit the amplification of the high-frequency noise, using the same parameters as in the 2015 data processing.

The input sky signal timeline is added to the convolved/deconvolved noise timeline and is then put through the instrument simulation. Note that the sky signal is not convolved/deconvolved with the bolometer time response, since it is already convolved with the scanning beam extracted from the 2015 TOI processing output which already contains the low-pass filter and residuals associated with the time-response deconvolution.

• Simulation of the signal non-linearity: the first step of electronics simulation is the conversion of the input sky plus noise signal from K_CMB units to analog-to-digital units (ADU) using the detector response measured on the ground and assumed to be stable in time. The ADU signal is then fed through a simulator of a non-linear analogue-to-digital converter (ADCNL). This step is the one introducing complexity into the signal, inducing time variation of the response, and causing gain differences with respect to the ground-based measurements. This corresponds to specific new correction steps in the mapmaking.

The ADCNL transfer-function simulation is based on the TOI processing, with correction from the ground measurements, combined with in-flight measurements. A reference simulation is built for each bolometer, which minimizes the difference between the simulation and the data gain variations, measured in a first run of the mapmaking. Realizations of the ADCNL are then drawn to mimic the variable behaviour of the gains seen in the 2018 data.

• Compression/decompression: the simulated signal is compressed by the algorithm required by the telemetry rate allocated to the HFI instrument, with a slight accuracy loss. While very close to the compression algorithm used on-board, the one used in the simulation pipeline differs slightly, due to the non-simulation of the cosmic-ray glitches, together with the use of the average of the signal in the compression slice.

The same number of compression steps as in flight data, the signal mean of each compression slice and the step value for each sample are then used by the decompression algorithm to reconstruct the modulated signal.

TOI processing

The TOIs issued from the steps above are then processed in the same way as the flight data. Because of the granularity needed and the computational performance required to produce hundreds of realizations, the TOI processing pipeline applied to the simulated data is highly optimized and slightly different from the one used for the data. The specific steps are the following:

• ADCNL correction: the ADCNL correction is carried out with the same parameters as the 2015 data TOI processing, and with the same algorithm. The difference between the realizations of ADC transfer function used for simulation and the constant one used for TOI processing is tuned to reproduce the gain variations found in 2015 processed TOI.

• Demodulation: signal demodulation is also performed in the same way as the flight TOI processing. First, the signal is converted from ADU to volts. Next, the signal is demodulated by subtracting from each sample the average of the modulated signal over 1 hour and then taking the opposite value for "negative" parity samples.

• Conversion to watts and thermal baseline subtraction: the demodulated signal is converted from volts to watts (neglecting the conversion non-linearity of the bolometers and amplifiers, which has been shown to be negligible). Eventually, the flight data thermal baseline, derived from the deglitched signals of the two dark bolometers smoothed over 1 minute, is subtracted.

• 1/f noise: a 1/f type noise component is added to the signal for each stable pointing period, with parameters (slope and knee frequency) adjusted on the flight data.

• Projection to HPR: the signal timeline is then projected and binned to HEALPix pixels for each stable pointing period (HEALPix rings, or HPR) after removal of flight-flagged data (unstable pointing periods, glitches, Solar system objects, planets, etc.).

• 4-K line residuals: a HPR of the 4-K line residuals for each bolometer, built by stacking the 2015 TOI, is added to the simulation output HPR.

Effects and processings not simulated

• no discrete point sources,
• no glitching/deglitching, only deglitching-induced noise auto-correlation,
• no 4-K line simulation and removal, only addition of their residuals,
• no bolometer volts-to-watts conversion non-linearity from the bolometers and amplifiers,
• no far sidelobes (FSLs),
• reduced simulation pipeline at 545 GHz and 857 GHz

To be more specific about this last item, the submillimetre channels simulation uses a pipeline without electronics simulation. It only contains photon and electronic noises, deglitching noise auto-correlation, time-response convolution/deconvolution, and 1/f noise. Bolometer by bolometer baseline addition and thermal baseline subtraction, compression/decompression, and 4-K line residuals are not included.

Mapmaking

The next stage is to use the SRoll mapmaking on the stim HPR. The following mapmaking inputs are all the same for simulation as for flight data:

• thermal dust, CO, and free-free map templates,
• detector NEP and polarization parameters,
• detector pointings,
• bad ring lists and sample flagging

The FSL removal performed in the mapmaking destriper is not activated (since no FSL contribution is included in the input). The total dipole removed by the mapmaking is the same as the input in the sky TOIs generated by LevelS (given in section 4.2. of Planck-2020-A3).

Post-processing

• Noise alignment: an additional noise component is added to more accurately align the noise levels of the simulations with the noise estimates built from the 2018 odd minus even ring maps. Of course, this adjustment of the noise level may not satisfy all the other noise null tests. This alignment is different for temperature and for polarization maps, in order to simulate the effect of the noise correlation between detectors within a PSB.

• Monopole adjustment: a constant value is added to each simulated map to bring its monopole to the same value as the corresponding 2018 map, which is described in section 3.1.1. of Planck-2020-A3.

• Signal subtraction: from each map, the input sky (CMB and foregrounds) is subtracted to build the “noise and residual systematics frequency maps.” These systematics include additional noise and residuals induced by sky-signal distortion. These maps are part of the FFP10 data set.

LFI E2E simulations

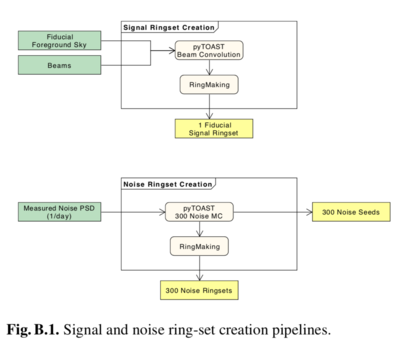
As described in Planck-2020-A2, the LFI systematic effect simulations are done partially at time- line and partially at ring-set level, with the goal of being as modular as possible, in order to create a reusable set of simulations. From the input sky model and according to the pointing information, we create single-channel ring-sets of the pure sky convolved with a suitable instrumental beam. To these we add pure noise (white and 1/ f ) ring-sets generated from the noise power spectrum distributions measured from real data one day at a time. The overall scheme is given in the Figure below:

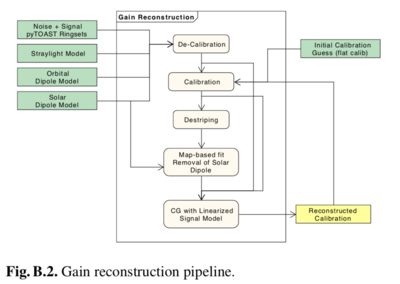
In the same manner, we create ring-sets for each of the specific systematic effects we would like to measure. We add together signal, noise, and systematic ring-sets, and, given models for straylight (based on the GRASP beams) and the orbital dipole, we create “perfectly-calibrated” ring-sets (i.e., calibration constant = 1). We use the gains estimate from the 2018 data release to “de-calibrate” these timelines, i.e., to convert them from kelvins to volts. At this point the calibration pipeline starts, and produces the reconstructed gains that will be different from the ones used in the de-calibration process due to the presence of simulated systematic effects. The calibration pipeline is algorithmically exactly the same as that used at the DPC for product creation, but with a different implementation (based principally on python). The gain-smoothing algorithm is the same as used for the data, and has been tuned to the actual data. This means that there will be cases where reconstructed gains from simulations differ significantly from the input ones. We have verified that this indeed happens, but only for very few pointing periods, and we therefore decided not to consider them in the following analysis. The overall process for estimating gains is given in the figure below:

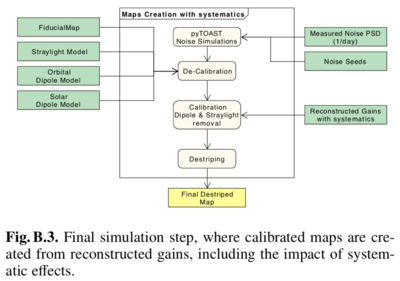
At this point we are able to generate maps for full mission, half-ring, and odd-even-year splits) that include the effects of systematic errors on calibration. In the final step, we produce timelines (which are never stored) starting from the same fiducial sky map, using the same model for straylight and the orbital dipole as in the previous steps, and from generated noise-only timelines created with the same seeds and noise model used before. We then apply the official gains to “de-calibrate” the timelines, which are immediately calibrated with the reconstructed gains in the previous step. The nominal destriping mapmaking algorithm is then used to create final maps. The complete data flow is given in the figure below:

Delivered Products

Input sky components

The separated input sky components generated by the Planck Sky Model are available for all frequencies, at HEALPix [math]N_{side}=1024[/math] or [math]2048[/math] or [math]4096[/math], depending on frequency:

	100GHz	143GHz	217GHz	353GHz	545GHz	857GHz
fiducial lensed scalar CMB
CO
free-free
synchrotron
far infrared background
kinetic SZ	100GHz kineticsz	143GHz kineticsz	217GHz kineticsz	353GHz kineticsz	545GHz kineticsz	857GHz kineticsz
Thermal SZ	100GHz thermalsz	143GHz thermalsz	217GHz thermalsz	353GHz thermalsz	545GHz thermalsz	857GHz thermalsz
faint infrared point sources	100GHz faintirps	143GHz faintirps	217GHz faintirps	353GHz faintirps	545GHz faintirps	857GHz faintirps
faint radio point sources	100GHz faintradiops	143GHz faintradiops	217GHz faintradiops	353GHz faintradiops	545GHz faintradiops	857GHz faintradiops
thermal dust

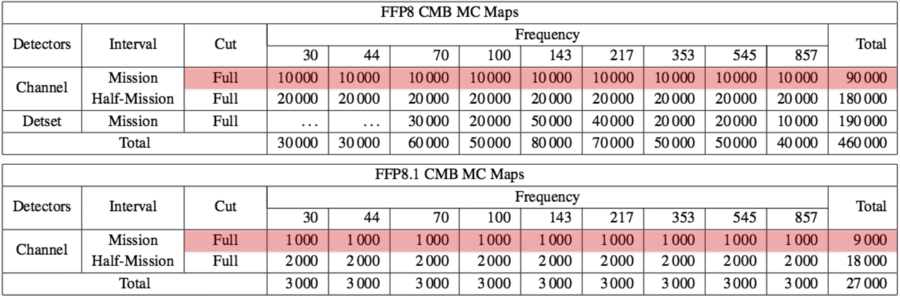
CMB realizations

The 1000 lensed scalar CMB map realizations are convolved with the FEBeCoP effective beams computed using the 2015 scanning beams (Planck-2015-A07, appendix B), and the updated scanning strategy described in the #PSM maps to timelines section above. Each CMB realization is available for the full-mission span only, at each frequency, which means 1000 realizations x 9 frequencies = 9000 CMB maps, which can be retrieved using the following link template:

http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=febecop_ffp10_lensed_scl_cmb_{frequency}_mc_{realization}.fits

where:

• {frequency} is any of frequency: 30, 44, 70, 100, 143, 217, 353, 545 or 857,
• {realization} is the realisation number, between 0000 and 0999, padded to four digits with leading zeros

For example: http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=febecop_ffp10_lensed_scl_cmb_100_mc_0000.fits

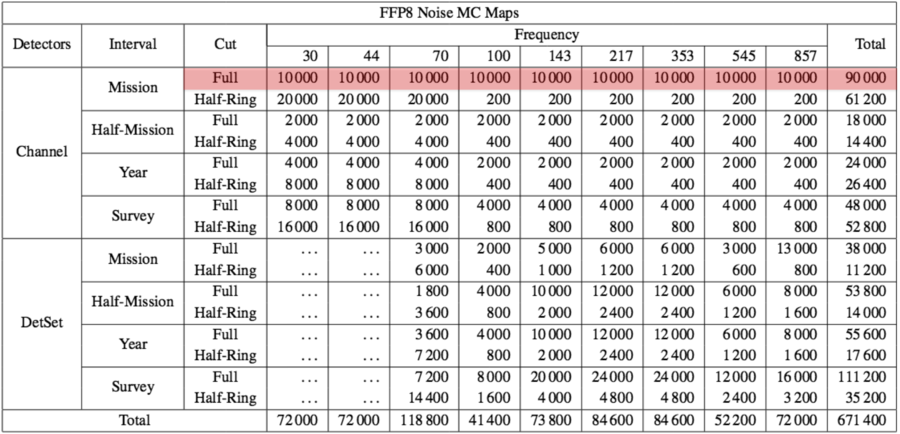
Noise and instrumental effect residual maps

HFI E2E maps

As described above, 300 realizations of full end-to-end simulations have been produced, to which the full sky signal part (CMB+foregrounds) have been subtracted in post-processing, to give maps of noise and systematic residuals only. For each realization and frequency, five data cuts are provided:

• full-mission,
• first and second half-missions,
• odd and even stable pointing periods (rings)

In addition to all 6 HFI frequencies, a special detector set made of only 353 GHz polarized bolometers (a.k.a 353_psb) is also published, to match the 2018 flight data set, for a total of 300 realizations x 5 data cuts x 7 HFI detector sets = 10,500 maps.

The noise maps can be retrieved from PLA using the following naming convention:

http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=ffp10_noise_{frequency}_{ring_cut}_map_mc_{realization}.fits

where:

• {frequency} is any of HFI frequency: 100, 143, 217, 353, 353_psb, 545 or 857,
• {ring_cut} is the ring selection scheme, one of: full, hm1, hm2, oe1, oe2
• {realization} is the realisation number, between 00000 and 00299, padded to five digits with leading zeros

For example: http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=ffp10_noise_100_full_map_mc_00000.fits

Please note that due to the specific polarization orientation of 100GHz bolometers, odd and even ring maps are badly conditionned for HEALPix [math]N_{side}=2048[/math] and are therefore also available at [math]N_{side}=1024[/math] by just replacing "_map_mc_" with "_map_1024_mc_" in the file link name.

LFI E2E maps

For LFI, a similar approach is followed as for HFI in terms of number and formatting of the E2E noise+systematics simulations.

Fiducial simulation

A separate full end-to-end simulation with a different CMB realization is also provided, with the full sky signal included and the same data cuts and detector sets as the 300 noise and systematic residual maps, to serve as a reference for whatever you would need it to. Please don't overlook the important warning below about thermal dust.

TODO: fiducial naming scheme

Two important warnings about noise and thermal dust

Noise

As stated in the introduction, FFP10 focus is on the simulation and correction of the main instrumental effects and systematics. It uses a noise model which doesn't vary in time, contrary to FFP8 simulations which used realizations of one noise power spectrum per stable pointing period and per detector. Doing so, all systematic residuals in FFP8 are considered as Gaussian noise, which time variations should follow the flight data.

If interested in Gaussian noise variations following flight data rather than non-Gaussian instrumental effects and systematic residuals, the user may want to check whether FFP8 noise maps better suit their needs. This is particularly true for 545 GHz and 857 GHz, for which FFP10 doesn't contain all instrumental effects and systematics and in which detectors' time response deconvolution is simulated at the noise-alignment post-processing step.

Thermal dust

After the production of the 300 realizations of noise and systematic residual simulations, a bug has been found in the PSM thermal dust template used as input, which led to a 10% intensity mismatch in temperature at 353 GHz due to a missing color correction. The same dust template has been correctly used for the simulations and for the sky subtraction post-processing, so the produced and published residual maps are not affected.

Note however, that the thermal dust maps provided as PSM input sky and the one used in the fiducial simulation are the fixed version of the PSM thermal dust, which slightly differs from the one used (and removed) in the 300 noise and systematic residual simulations.

Other Releases: 2020-NPIPE, 2015 and 2013 simulated maps

2020 Release of simulated maps (NPIPE)

The NPIPE release includes 600 simulated full-frequency and detector-set Monte Carlo realizations. 100 of those realizations include single-detector and half-ring maps.

NPIPE simulations include all of the reprocessing steps, but only approximate the effects of preprocessing. The approximation is based on simulating the detector noise from a power spectral density (PSD) measured from preprocessed time-ordered data.

The components of the full signal simulations are:

• CMB signal, consisting of independent CMB realisations convolved on-the-fly with the asymmetric detector beams and including the solar system and orbital dipole;
• foregrounds, consisting of a Commander sky model evaluated at each frequency;
• zodiacal light, based on fits of the zodiacal templates on real data;
• bandpass mismatch, based on real data fits of the mismatch templates;
• LFI gain fluctuations, consisting of smoothed versions of the noisy fits of real data;
• instrumental noise, based on measured noise in preprocessed data, including cross-detector correlated noise.

In addition, fitting for the full suite of reprocessing templates adds all potential template degeneracies and pipeline transfer function effects.

Each full signal simulation is accompanied with a symmetric beam-convolved CMB map, foreground map, and a residual (noise) map created by regressing out the input signals from the full map.

Simulated NPIPE maps derive from a time-domain simulation that includes beam-convolved CMB, bandpass-mismatched foregrounds, and instrumental 1/f noise with realistic intra horn correlations. Seasonal gain fluctuations are added into the simulated LFI signal by smoothing the measured real data gain fluctuation. The data are processed with the same reprocessing module as the real data, introducing similar large-scale systematics and correlations.

CMB

The simulated CMB is the same as used in PR3 simulations. Instead of processing the CMB in the map-domain, NPIPE uses libconviqt to convolve the CMB with individual detector beams at appropriate orientations. Simulating full time-domain processing allows the user to assess potential pipeline transfer function effects relevant to their analysis. This is in contrast to PR3 where the CMB simulations were performed in the map domain.

The parameters of the simulated CMB are shown in the following table, reproduced from A&A 643, A42 (2020).

Foregrounds

Unlike the CMB, there is only one realization of the foregrounds. They are based on the Commander sky model, evaluated at the nominal central frequency for each band. Sky-model component maps that are noise-dominated outside the Galactic plane are smoothed to remove unphysical levels of small-scale structure from the simulation. Without this smoothing the simulated 30-GHz maps showed a significant excess of extra-Galactic power when compared to the real data maps.

Bandpass mismatch is simulated by adding bandpass-mismatch templates to the frequency map before sampling it into the map domain. The template amplitudes are based on real data fits.

Since the Commander sky model used as input already includes beam smoothing, we do not convolve with the instrumental beam as we do with the CMB.

Noise

Instrumental noise is simulated from mission-averaged noise PSDs. We use the Fourier technique to create noise realizations that conform to the full PSD, not just a parametrized noise model. Correlated noise between detectors in a single horn reduces the horn's sensitivity to sky temperature but not polarization. We use the measured detector cross-spectra to account for this phenomenon.

Simulated maps

100 Monte Carlo realizations are available on the PLA. These include full-frequency maps, A/B splits, and single-detector maps. For convenience, we provide total signal and residual maps. Matching SEVEM-processed CMB and noise maps are also made available.

CMB realizations

Input CMB maps convolved with a symmetrized beam are available using the following link template:

http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=npipe6v20{subset}_cmb_input_{frequency}_map_mc_{realization}.fits

Here:

• {subset} is "", "A", or "B";
• {frequency} is any of 030, 044, 070, 100, 143, 217, 353, 545, or 857;
• {realization} is the realization number, between 0200 and 0299, padded to four digits with leading zeros.

For example: http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=npipe6v20_cmb_030_A_mc_00299.fits

Residual maps

Simulated residual maps (output - input) can be downloaded with the following link template:

http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=npipe6v20{subset}_noise_{frequency}_map_mc_{realization}.fits

Here:

• {subset} is "", "A", or "B";
• {frequency} is any of: 030, 044, 070, 100, 143, 217, 353, 545, or 857;
• {realization} is the realization number, between 0200 and 0299, padded to four digits with leading zeros.

For example: http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=npipe6v20_noise_030_A_mc_00200.fits

Commander maps

Simulated Commander CMB maps are available at

http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=npipe6v20{subset}_sevem_cmb_mc_{realization}_raw.fits

Here:

• {subset} is "", "A", or "B";
• {realization} is the realization number, between 0200 and 0299, padded to four digits with leading zeros.

Matching foreground-subtracted frequency maps can be retrieved with, for example:

http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=npipe6v20_commander_cmb_2048_mc_0300_005a.fits

Here:

• {subset} is "", "A", or "B";
• {frequency} is any of 070, 100, 143, or 217;
• {realization} is the realization number, between 0200 and 0299, padded to four digits with leading zeros.

2015 Release of simulated maps

Introduction

The 2015 Planck data release is supported by a set of simulated maps of the sky, by astrophysical component, and of that sky as seen by Planck (fiducial mission realizations), together with separate sets of Monte Carlo realizations of the CMB and the instrument noise.

Currently, only a subset of these simulations is available from the Planck Legacy Archive. In particular:

• 18000 full mission CMB simulations: 1000 for each of the nine Planck frequencies, and for two different sets of cosmological parameters.
• 9000 full mission noise simulations: 1000 for each of the nine Planck frequencies.
• 18 full mission sky simulated maps: two sets of sky maps with and without bandpass corrections applied.

The first two types of simulations, CMB and noise, that are only partially available in the PLA, and the sky simulated maps, have been highlighted in red in Table 1.

The full set of Planck simulations can be found in the NERSC supercomputing center. Instructions on how to access and retrieve the data can be found in HERE.

They contain the dominant instrumental (detector beam, bandpass, and correlated noise properties), scanning (pointing and flags), and analysis (map-making algorithm and implementation) effects. These simulations have been described in Planck-2015-A12.

In addition to the baseline maps made from the data from all detectors at a given frequency for the entire mission, there are a number of data cuts that are mapped both for systematics tests and to support cross-spectral analyses. These include:

• detector subsets (“detsets”), comprising the individual unpolarized detectors and the polarized detector quadruplets corresponding to each leading trailing horn pair. Note that HFI sometimes refers to full channels as detset0; here detset only refers to subsets of detectors.
• mission subsets, comprising the surveys, years, and half-missions, with exact boundary definitions given in Planck-2015-A02 and Planck-2015-A07 for LFI and HFI, respectively.
• half-ring subsets, comprising the data from either the first or the second half of each pointing-period ring

The various combinations of these data cuts then define 1134 maps, as enumerated in the top section of Table 1 from Planck-2015-A12. The different types of map are then named according to their included detectors (channel or detset), interval (mission, half-mission, year or survey), and ring-content (full or half-ring); for example the baseline maps are described as channel/mission/full, etc.

The simulation process consists of

• modelling each astrophysical component of the sky emission for each Planck detector, using Planck data and the relevant characteristics of the Planck instruments.
• simulating each detector's observation of each sky component following the Planck scanning strategy and using the best estimates of the detector's beam and noise properties (obtained in flight), then combining these timelines into a single one per detector, and projecting these simulated timelines onto observed maps (the fiducial sky), as is done with the on-orbit data;
• generating Monte Carlo realizations of the CMB and of the noise, again following the Planck scanning strategy and using our best estimates of the detector beams and noise properties respectively.

The first step is performed by the Planck Sky Model (PSM), and the last two by the Planck Simulation Tools (PST), both of which are described in the sections below.

The production of a full focal plane (FFP) simulation, and including the many MC realizations of the CMB and the noise, requires both HFI and LFI data and includes large, computationally challenging, MC realizations. They are too large to be generated on either of the DPC's own cluster. Instead the PST consists of three distinct tools, each designed to run on the largest available supercomputers, that are used to generate the fiducial sky realization, the CMB MC, and the noise MC respectively. The simulations delivered here are part of the 8th generation FFP simulations, known as FFP8. They were primarily generated on the National Energy Research Scientific Computing Center (NERSC) in the USA and at CSC–IT Center for Science (CSC) in Finland.

The fiducial realizations include instrument noise, astrophysical foregrounds, and the lensed scalar, tensor, and non-Gaussian CMB components, and are primarily designed to support the validation and verification of analysis codes. To test our ability to detect tensor modes and non-Gaussianity, we generate five CMB realizations with various cosmologically interesting — but undeclared — values of the tensor-to-scalar ratio r and non-Gaussianity parameter f_NL. To investigate the impact of differences in the bandpasses of the detectors at any given frequency, the foreground sky is simulated using both the individual detector bandpasses and a common average bandpass, to include and exclude the effects of bandpass mismatch. To check that the PR2-2015 results are not sensitive to the exact cosmological parameters used in FFP8 we subsequently generated FFP8.1, exactly matching the PR2-2015 cosmology.

Table 1 of Planck-2015-A12. The numbers of fiducial, MC noise and MC CMB maps at each frequency by detector subset, data interval, and data cut.

Since mapmaking is a linear operation, the easiest way to generate all of these different realizations is to build the full set of maps of each of six components:

1. the lensed scalar CMB (cmb_scl);
2. the tensor CMB (cmb_ten);
3. the non-Gaussian complement CMB (cmb_ngc);
4. the forgreounds including bandpass mismatch (fg_bpm);
5. the foregrounds excluding bandpass mismatch (fg_nobpm);
6. the noise.

We then sum these, weighting the tensor and non-Gaussian complement maps with [math]\sqrt{r}[/math] and f_NL, respectively, and including one of the two foreground maps, to produce 10 total maps of each type. The complete fiducial data set then comprises 18,144 maps.

While the full set of maps can be generated for the fiducial cases, for the 10⁴-realization MC sets this would result in some 10⁷ maps and require about 6 PB of storage. Instead, therefore, the number of realizations generated for each type of map is chosen to balance the improved statistics it supports against the computational cost of its generation and storage. The remaining noise MCs sample broadly across all data cuts, while the additional CMB MCs are focused on the channel/half-mission/full maps and the subset of the detset/mission/full maps required by the "commander" component separation code Planck-2015-A10.

Mission and instrument characteristics The goal of FFP8 is to simulate the Planck mission as accurately as possible; however, there are a number of known systematic effects that are not included, either because they are removed in the pre-processing of the time-ordered data (TOD), or because they are insufficiently well-characterized to simulate reliably, or because their inclusion (simulation and removal) would be too computationally expensive. These systematic effects are discussed in detail in Planck-2015-A02 and Planck-2015-A07 and include:

• cosmic ray glitches (HFI);
• spurious spectral lines from the 4-K cooler electronics (HFI);
• non-linearity in the analogue-to-digital converter (HFI);
• imperfect reconstruction of the focal plane geometry.

Note that if the residuals from the treatment of any of these effects could be mapped in isolation, then maps of such systematics could simply be added to the existing FFP8 maps to improve their correspondence to the real data.

Pointing The FFP8 detector pointing is calculated by interpolating the satellite attitude to the detector sample times and by applying a fixed rotation from the satellite frame into the detector frame. The fixed rotations are determined by the measured focal plane geometry as shown in Planck-2015-A04 and Planck-2015-A07, while the satellite attitude is described in the Planck attitude history files (AHF). The FFP pointing expansion reproduces the DPC pointing to sub-arcsecond accuracy, except for three short and isolated instances during Surveys 6—8 where the LFI sampling frequency was out of specification. Pixelization of the information causes the pointing error to be quantized to either zero (majority of cases) or the distance between pixel centres (3.4' and 1.7' for LFI and HFI, respectively). Since we need a single reconstruction that will serve both instruments efficiently in a massively parallel environment, we use the pointing provided by the Time Ordered Astrophysics Scalable Tools (Toast) package.

Noise We require simulated noise realizations that are representative of the noise in the flight data, including variations in the noise power spectral density (PSD) of each detector over time. To obtain these we developed a noise estimation pipeline complementary to those of the DPCs. The goal of DPC noise estimation is to monitor instrument health and to derive optimal noise weighting, whereas our estimation is optimized to feed into noise simulation. Key features are the use of full mission maps for signal subtraction, long (about 24 hour) realization length, and the use of auto-correlation functions in place of Fourier transforms to handle flagged and masked data (HFI).

Beams The simulations use the so-called scanning beams (e.g., Planck-2013-VI), which give the point-spread function of for a given detector including all temporal data processing effects: sample integration, demodulation, ADC non-linearity residuals, bolometric time constant residuals, etc. In the absence of significant residuals (LFI), the scanning beams may be estimated from the optical beams by smearing them in the scanning direction to match the finite integration time for each instrument sample. Where there are unknown residuals in the timelines (HFI), the scanning beam must be measured directly from observations of strong point-like sources, namely planets. If the residuals are present but understood, it is possible to simulate the beam measurement and predict the scanning beam shape starting from the optical beam.

For FFP8, the scanning beams are expanded in terms of their spherical harmonic coefficients, [math]b_{\ell m}[/math], with the order of the expansion (maximum [math]\ell[/math] and m considered) representing a trade-off between the accuracy of the representation and the computational cost of its convolution. The LFI horns have larger beams with larger sidelobes (due to their location on the outside of the focal plane), and we treat them as full [math]4\pi[/math] beams divided into main (up to 1.9°, 1.3°, and 0.9° for 30, 44, and 70 GHz, respectively), intermediate (up to 5°), and sidelobe (above 5°) components Planck-2015-A04. This division allows us to tune the expansion orders of the three components separately. HFI horns are limited to the main beam component, measured out to 100 arc minutes Planck-2015-A07. Since detector beams are characterized independently, the simulations naturally include differential beam and pointing systematics.

Bandpasses Both the LFI and HFI detector bandpasses are based on ground measurements (see Planck-2013-IX, respectively), although flight data processing for LFI now uses in-flight top-hat approximations rather than the ground measurements that were found to contain systematic errors. Differences in the bandpasses of detectors nominally at the same frequency (the so-called bandpass mismatch) generate spurious signals in the maps, since each detector is seeing a slightly different sky while the mapmaking algorithms assume that the signal in a pixel is the same for all detectors. To quantify the effect of these residuals, in FFP8 we generate detector timelines from foreground maps in two ways, one that incorporates the individual detector bandpasses, the other using an average bandpass for all the detectors at a given frequency.

This effect of the bandpass mismatch can be roughly measured from either flight or simulated data using so-called spurious component mapmaking, which provides noisy all-sky estimates of the observed sky differences (the spurious maps), excluding polarization, between individual detectors and the frequency average. We compare the amount of simulated bandpass mismatch to flight data. The spurious component approach is detailed in the Appendix of Planck-2015-A12. Mismatch between FFP8 and flight data is driven by inaccurate bandpass description (LFI) and incomplete line emission simulation (HFI). The noisy pixels that align with the Planck scanning rings in the HFI maps are regions where the spurious map solution is degenerate with polarization due to insufficient observation orientations.

The Planck Sky Model

The Planck Sky Model, PSM, consists of a set of data and of code used to simulate sky emission at millimeter-wave frequencies; it is described in detail in Delabrouille et al., (2013), henceforth the PSM paper.

The Planck Sky Model is available here: http://www.apc.univ-paris7.fr/~delabrou/PSM/psm.html

The main simulations used to test and validate the Planck data analysis pipelines (and, in particular, component separation) makes use of simulations generated with version 1.9 of the PSM software. The total sky emission is built from the CMB plus ten foreground components, namely thermal dust, spinning dust, synchrotron, CO lines, free-free, thermal Sunyaev-Zel'dovich (SZ) effect (with first order relativistic corrections), kinetic SZ effect, radio and infrared sources, Cosmic Infrared Background (CIB).

The CMB is modelled using CAMB. It is based on adiabatic initial perturbations, with the following cosmological parameters as listed in Table 3 of Planck-2015-A07

Galactic and extragalactic components

The Galactic ISM emission comprises five components: thermal dust, spinning dust, synchrotron, free-free, CO lines (the J=1->0, J=2->1, and J=3->2 lines at 115.27, 230.54, and 345.80 GHz, respectively), and plus the cosmic infrared background (CIB), emission from radio sources, and the thermal and kinetic Sunyaev-Zeldovich (SZ) effects.

The thermal dust emission is modelled using single-frequency template maps of the intensity and polarization, together with a pixel-dependent emission law. For FFP8 the thermal dust emission templates are derived from the Planck 353 GHz observations. This update of the original PSM dust model is necessary to provide a better match to the emission observed by Planck. While one option would be simply to use the dust opacity map obtained in Planck-2013-XI, this map still suffers from significant contamination by CIB anisotropies and infrared point sources. Using it as a 353 GHz dust template in simulations would result in an excess of small scale power (from CIB and infrared sources) scaling exactly as thermal dust across frequencies. The resulting component represents correctly neither dust alone (because of an excess of small scale power) nor the sum of dust and infrared sources (because the frequency scaling of the CIB and infrared sources is wrong). For simulation purposes, the main objective is not to have an exact map of the dust, but instead a map that has the right statistical properties. Hence we produce a template dust map at 353 GHz by removing that fraction of the small-scale power that is due to CIB emission, infra-red sources, CMB, and noise.

The spinning-dust map used for FFP8 simulations is a simple realization of the spinning dust model, post-processed to remove negative values occurring in a few pixels because of the generation of small-scale fluctuations on top of the spinning dust template extracted from WMAP data.

The FFP8 synchrotron emission is modelled on the basis of the template emission map observed at 408 MHz by Haslam et al. (1982). This template synchrotron map is extrapolated in frequency using a spectral index map corresponding to a simple power law.

The free-free spectral dependence is modelled in FFP8 by assuming a constant electron temperature [math]T_{e}[/math] = 7000 K. Electron-ion interactions in the ionized phase of the ISM produce emission that is in general fainter than both the synchrotron and the thermal dust emission outside of the active star-forming regions in the Galactic plane. The free-free model uses a single template, which is scaled in frequency by a specific emission law. The free-free spectral index is a slowly varying function of frequency and depends only slightly on the local value of the electron temperature.

The radio sources are modelled in FFP8 in a different way from the pre-launch versions of the PSM.

For strong radio sources ([math]S_{30}[/math] > 0.5 Jy), we use radio sources at 0.84, 1.4, or 4.85 GHz. For sources observed at two of these frequencies, we extrapolate or interpolate to the third frequency assuming the spectral index estimated from two observed. For sources observed at only one frequency, we use differential source counts to obtain the ratio of steep- to flat-spectrum sources in each interval of flux density considered. From this ratio, we assign spectral indices (randomly) to each source within each flux density interval. Fiducial Gaussian spectral index distributions as a function of spectral class are obtained from the literature. These are then adjusted slightly until there is reasonable agreement between the PSM differential counts and the predicted model counts predicted.

For faint radio sources ([math]S_{30}[/math] <= 0.5 Jy), the pre-launch PSM showed a deficit of sources resulting from inhomogeneities in surveys at different depths. We address this issue by constructing a simulated catalogue of sources at 1.4 GHz. We replace the simulated sources by the observed ones, wherever possible. If, however, in any particular pixel, we have a shortfall of observed sources, we make up the deficit with the simulated sources. Every source in this new catalogue is given a model-derived spectral class. We thus assign a spectral index to each source based on the spectral class, and model the spectrum of each source using four power laws. We also assume some steepening of the spectral index with frequency, with fiducial values of the steepening obtained from the literature.

We combine the faint and strong radio source catalogues we constructed and compute the differential source counts on these sources between 0.005 Jy and 1 Jy. Finally we also model the polarization of these radio sources using the measured polarization fractions from the literature; for each simulated source we draw a polarization fraction at random from the list of real sources of the same spectral type.

The SZ clusters are simulated following the model of Delabrouille, Melin, and Bartlett (DMB) as implemented in the PSM. A catalogue of halos is drawn from a Poisson distribution of the mass function with a limiting mass of M_500,true > 2x10¹³[math]M_\odot[/math]. We use the pressure profile from the literature to model the thermal SZ emission of each halo given its redshift and mass. We determine the cluster temperature and assume that the profiles are isothermal. These steps allow us to compute the first-order thermal relativistic correction and the kinetic SZ effect for each cluster, both of which are included in the simulation. Finally, we inject catalogued clusters following the same model, and remove from the simulation corresponding clusters in each redshift and mass range. Hence the SZ simulation features the majority of known X-ray and optical clusters, and is fully consistent with X-ray scaling laws and observed Planck SZ counts.

The CIB model used to simulate FFP8 relies on the distribution of individual galaxies in template maps based on the distribution of dark matter at a range of relevant redshifts. We assume the CIB galaxies can be grouped into three different populations (proto-spheroid, spiral, starburst). Within each population, galaxies have the same SED, while the flux density is randomly distributed according to redshift-dependent number counts obtained from JCMT/SCUBA-2 observations and the Planck ERCSC, as well as observations from Herschel-SPIRE and AzTEC/ASTE. We use the Class software to generate dark matter maps at 17 different redshifts between 1 and 5.5. Since the galaxy distribution does not exactly follow the dark matter distribution, we modify the a_lm coefficients of dark matter anisotropies given by Class. Template maps generated from the a_lm coefficients are then exponentiated to avoid negative pixels. Galaxies are randomly distributed with a probability of presence proportional to the pixel values of the template maps. One map is generated for each population, at each redshift, and associated with a redshifted SED depending on the population. The emission of these maps (initially at a reference frequency) can be extrapolated to any frequency using the associated redshifted SED. By summing the emission of all maps, we can generate CIB maps at any frequency in the range of validity of our model.

See Planck-2015-A12 and references therein for a very detailed explanation of the procedures to simulate each of the components.

The sky model is simulated at a resolution common to all components by smoothing the maps with an ideal Gaussian beam of FWHM of 4 arcminute. The Healpix [1] pixelization in Galactic coordinates is used for all components, with Nside = 2048 and [math]\ell_{max}[/math] = 6000. Sky emission maps are generated by numerically band-integrating the sky model maps (emission law of each component, in each pixel) over the frequency bands both of each detector in the focal plane and — using an average over the detectors at a given frequency — of each channel. The band-integrated maps are essentially observations of the model sky simulated by an ideal noiseless instrument with ideal Gaussian beams of FWHM equal to the resolution of the model sky.

The CMB Sky

The CMB sky is simulated in three distinct components, namely lensed scalar, tensor, and non-Gaussian complement. The total CMB sky is then the weighted sum with weights 1, [math]\sqrt{r}[/math], and f__NL, respectively. For FFP8, all CMB sky components are produced as spherical harmonic representations of the I, Q, and U skies.

The FFP8 CMB sky is derived from our best estimate of the cosmological parameters available at the time of its generation, namely those from the first Planck data release Planck-2013-I, augmented with a judicious choice of reionization parameter [math]\tau[/math], as listed in Table 3 of Planck-2015-A12.

The scalar CMB sky

The scalar component of the CMB sky is generated including lensing, Rayleigh scattering, and Doppler boosting effects.

• Using the Camb code, we first calculate fiducial unlensed CMB power spectra [math]C_{\ell}^{TT}[/math], [math]C_{\ell}^{EE}[/math], [math]C_{\ell}^{TE}[/math], the lensing potential power spectrum [math]C_{\ell}^{\phi\phi}[/math], and the cross-correlations [math]C_{\ell}^{T\phi}[/math] and [math]C_{\ell}^{E\phi}[/math]. We then generate Gaussian T, E, and [math]\phi[/math] multipoles with the appropriate covariances and cross-correlations using a Cholesky decomposition and three streams of random Gaussian phases. These fields are simulated up to [math]\ell_{max}[/math]=5120.

• Add a dipole component to [math]\phi[/math] to account for the Doppler aberration due to our motion with respect to the CMB. UPDATE: Note that although it was intended to include this component in this set of simulations, in the end it was not. It will be included in future versions of the simulation pipeline.

• Compute the effect of gravitational lensing on the temperature and polarization fields, using an algorithm similar to LensPix. We use a fast spherical harmonic transform to compute the temperature, polarization, and deflection fields. The unlensed CMB fields T, Q, and U are evaluated on an equicylindrical pixelization (ECP) grid with [math]N_{\theta}=32\,768[/math] and [math]N_{\varphi} = 65\,536[/math], while the deflection field is evaluated on a Healpix Nside=2048 grid. We then calculate the "lensed positions for each Nside=2048 Healpix pixel. We then interpolate T, Q, U at the lensed positions using 2-D cubic Lagrange interpolation on the ECP grid.

• Incorporate the frequency-dependent Doppler modulation effect Planck-2013-XXVII.

• Evaluate lensed, Doppler boosted [math]T_{\ell m}[/math], [math]E_{\ell m}[/math], and [math]B_{\ell m}[/math] up to [math]\ell_{max}=4\,096[/math] with a harmonic transform of the Nside=2048 Healpix map of these interpolated T, Q, and U values.

• Add frequency-dependent Rayleigh scattering effects.

• Add a second-order temperature quadrupole. Since the main Planck data processing removes the frequency-independent partPlanck-2015-A08, we simulate only the residual frequency-dependent temperature quadrupole. After subtracting the frequency-independent part, the simulated quadrupole has frequency dependence [math]\propto (b_{\nu}-1)/2[/math], which we calculate using the bandpass-integrated [math]b_{\nu}[/math] boost factors given in Table 4 of Planck-2015-A12.

The tensor CMB sky In addition to the scalar CMB simulations, we also generate a set of CMB skies containing primordial tensor modes. Using the fiducial cosmological parameters of Table 3 of Planck-2015-A12, we calculate the tensor power spectra [math]C_{\ell}^{TT, {\rm tensor}}[/math], [math]C_{\ell}^{EE, {\rm tensor}}[/math], and [math]C_{\ell}^{BB, {\rm tensor}}[/math] using Camb with a primordial tensor-to-scalar power ratio [math]r=0.2[/math] at the pivot scale [math]k=0.05\,Mpc^{-1}[/math]. We then simulate Gaussian T, E, and B-modes with these power spectra, and convert these to spherical harmonic representations of the corresponding I, Q and U maps. Note that the default r=0.2 means that building the FFP8a-d maps requires rescaling each CMB tensor map by [math]\sqrt{r/0.2}[/math] for each of the values of r in Table 2 of Planck-2015-A12.

The non-Gaussian CMB sky We use a new algorithm to generate simulations of CMB temperature and polarization maps containing primordial non-Gaussianity. Non-Gaussian fields in general have a non-vanishing bispectrum contribution sourced by mode correlations. The bispectrum, the Fourier transform of the 3-point correlation function, can then be characterized as a function of three wavevectors, [math]F(k_1, k_2, k_3)[/math]. Depending on the physical mechanism responsible for generating the non-Gaussian signal, it is possible to introduce broad classes of model that are categorized by the dependence of F on the type of triangle formed by the three momenta [math]k_i[/math]. Here, we focus on non-Gaussianity of local type, where the bulk of the signal comes from squeezed triangle configurations, [math]k_1 \ll k_2 \approx k_3[/math]. This is typically predicted by multi-field inflationary models. See Section 3.3.3 of Planck-2015-A12 for further details on the simulation of this components and references.

The FFP8.1 CMB skies

The FFP8 simulations are an integral part of the analyses used to derive PR2-2015, and so were necessarily generated prior to determining that release's cosmological parameters. As such there is inevitably a mismatch between the FFP8 and the PR2-2015 cosmologies, which we address in two ways. The quick-and-dirty fix is to determine a single rescaling factor that minimizes the difference between the PR1-2013 and PR2-2015 TT power spectra and apply it to all of the FFP8 CMB maps; this number is determined to be 1.0134, and the rescaled maps have been used in several repeat analyses to confirm the robustness of various PR2-2015 results.

More rigorously though, we also generate a second set of CMB realizations based on the PR2-2015 cosmology, dubbed FFP8.1, and perform our reanalyses using these in place of the FFP8 CMB skies in both the fiducial and MC realizations. Table 3 of Planck-2015-A12 lists the cosmological parameters used for FFP8.1 while Table 1 of Planck-2015-A12 enumerates the current status of the FFP8.1 CMB MCs.

The Fiducial Sky Simulations

The FFP8 fiducial realization is generated in two steps:

1. Simulation of the full mission TOD for every detector
2. Calculation of maps from the various detector subsets, intervals, and data cuts.

Simulation of explicit TODs allows us to incorporate each detector's full beam (including its far sidelobes) and unique input sky (including its bandpass). As noted above, the fiducial realization is generated in six separate components — the three CMB components (lensed scalar, tensor, and non-Gaussian complement), two foreground realizations (with and without bandpass mismatch), and noise. The first five of these are simulated as explicit TODs and then mapped, while the noise is generated using the on-the-fly approach described in the noise MC subsection below.

TOD generation for any detector proceeds by:

1. Convolving the appropriate sky component with the beam at every point in a uniformly sampled data cube of Euler angle triplets (encoding the pointing and polarization orientation) to produce the "beamskyset".
2. Generating the time-ordered data by interpolating over the beamskyset data cube to the exact pointing and polarization orientation of each sample.

Previous FFP simulations, including FFP6, accompanying the 2013 Planck data release, used the LevelS software package to do this. However, this required format conversions for the input pointing data and the output time-ordered data, at significant IO and disk space costs. For FFP8 we have therefore embedded the critical parts of these routines into a new code which uses Toast to interface directly with exchange format data.

All of the FFP8 fiducial maps are produced using Madam/Toast, a Toast port of the Madam generalized destriping code, which allows for destriping with an arbitrary baseline length, with or without a prior on the baseline distribution (or noise filter). Madam is used to produce the official LFI maps, and its destriping parameters can be chosen so that it reproduces the behaviour of Polkapix, the official HFI mapmaking code. Comparison of the official maps and Madam/Toast maps run using exchange data show that mapmaker differences are negligible compared to small differences in pointing and (for HFI) dipole subtraction that do not impact the simulation. The sky components are mapped from the TODs, while the fiducial noise is taken to be realization 10000 of the noise MC (with realizations 0000-9999 reserved for the noise MC itself).

Summarizing the key differences in the map making parameters for each Planck frequency:

• 30 GHz is destriped with 0.25 s baselines; 44 and 70 GHz are destriped using 1 s baselines; and 100—857 GHz are destriped using pointing-period baselines (30-75 min).

• 30—70 GHz are destriped with a 1/f-shape noise prior, while 100—857 GHz are destriped without a noise prior.

• 30, 44, and 70 GHz have separate destriping masks, while 100—857 GHz use the same 15% galaxy + point source mask.

• 30—70 GHz maps are destriped using baselines derived exclusively from the data going into the particular map, while 100-857 GHz maps are destriped using baselines derived from the full data set.

Noise MC

The FFP8 noise MCs are generated using Madam/Toast, exploiting Toast's on-the-fly noise simulation capability to avoid the IO overhead of writing a simulated TOD to disk only to read it back in to map it. In this implementation, Madam runs exactly as it would with real data, but whenever it submits a request to Toast to provide it with the an interval of the noise TOD, that interval is simply simulated by Toast in accordance with the noise power spectral densities provided in the runconfig, and returned to Madam.

For a simulation set of this size and complexity, requiring of the order of [math]10^{17}[/math] random numbers over [math]10^{12}[/math] disjoint and uncorrelated intervals, care must be take with the pseudo-random number generation to ensure that it is fast, reliable (and specifically uncorrelated), and reproducible, in particular enabling any process to generate any element of any subsequence on demand. To achieve this Toast uses a Combined Multiple Recursive Generator (CMRG) that provides more than sufficient period, excellent statistical robustness, and the ability to skip ahead to an arbitrary point in the pseudo-random sequence very quickly. See Planck-2015-A12 for further details on the Noise MCs.

CMB MC

The FFP8 CMB MCs are generated using the Febecop software package, which produces beam-convolved maps directly in the pixel domain rather than sample-by-sample, as is done for the fiducial maps. The goal of this approach is to reduce the computational cost by the ratio of time-samples to map-pixels (i.e., the number of hits per pixel).

The Febecop software package proceeds as follows:

1. Given the satellite pointing and flags and the focal plane (accessed through the Toast interface), for every channel Febecop first re-orders all of the samples in the mission by pixel instead of time, localizing all of the observations of each pixel, and writes the resulting pixel-ordered detector dngles (PODA) to disk. Note that since the PODA also contains the detector, time-stamp, and weight of each observation this is a one-time operation for each frequency, and does not need to be re-run for different time intervals or detector subsets, or for changes in the beam model or its chosen cut-off radius.

1. For every time interval and detector subset to be mapped, and for every pixel in the map, Febecop uses the PODA and the scanning beams to generate an effective-beam for that pixel which is essentially the weighted average of the discretized beam functions for every sample in the pixel included in the time interval and detector subset. The total effective-beam array is also written to disk. Given the PODA, this is a one-time operation for any beam definition.

1. Finally, Febecop applies the effective-beam pixel-by-pixel to every CMB sky realization in the MC set to generate the corresponding beam-convolved CMB map realization.

The effective-beams provide a direct connection between the true and observed sky, explicitly incorporating the detailed pointing for every detector through a linear convolution. By providing the effective-beams at every pixel, Febecop enables precise control of systematic effects, e.g., the point-spread functions can be fitted at each pixel on the sky and used to determine point source fluxes Planck-2015-A26 and Planck-2015-A27

Validation Our goal for the FFP8 simulation set is that it be not only internally self-consistent, but also a good representation of the real data. In addition to the validation steps carried out on all of the inputs individually and noted in their respective sections above, we must also validate the final outputs. A first crude level of validation is provided simply by visual inspection of the FFP8 and real Planck maps where the only immediately apparent difference is the CMB realization.

While this is a necessary test, it is hardly sufficient, and the next step is to compare the angular power spectra of the simulated and real channel/mission/full maps. As illustrated in Planck-2015-A26, LFI channels show excellent agreement across all angular scales, while HFI channels show a significant power deficit at almost all angular scales. Since this missing HFI power is not picked up in the noise estimation, it must be sky-synchronous (frequency bins corresponding to sky-synchronous signals being discarded when fitting the noise PSDs due to their contamination by signal residuals). This is now understood to be a systematic effect introduced in the HFI pre-processing pipeline, and we are working both to incorporate it as a systematic component in existing simulations and to ameliorate if for future data releases.

Finally, the various analyses of the FFP8 maps in conjunction with the flight data provide powerful incidental validation. To date the only issues observed here are the known mismatch between the FFP8 and PR2-2015 cosmologies, and the missing systematic component in the HFI maps. As noted above, the former is readily addressed by rescaling or using FFP8.1; however, the characterization and reproduction of the latter is an ongoing effort. Specific details of the consequences of this as-yet unresolved issue, such as its impact on null-test failures and p-value stability in studies of non-Gaussianity. In addition, as stated above, the CMB simulations containing only the modulation but not aberration part of the Doppler boost signal.

Delivered products

Fiducial Sky

There are 9 PSM simulations of the fiducial sky that correspond to the simulated sky integrated over the average spectral response of each band, but not convolved with the beam. They can be downloaded from the PLA or directly here:

• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-030_1024_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-044_1024_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-070_1024_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-100_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-143_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-217_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-353_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-545_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-857_2048_R2.00_full.fits

In addition, a set of 9 simulations of the fiducial sky corrected for bandpass mismatch (nobpm) can be obtained here:

• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-030_1024_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-044_1024_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-070_1024_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-100_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-143_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-217_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-353_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-545_2048_R2.00_full.fits
• http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-857_2048_R2.00_full.fits

Sky simulated maps file data structure

1. EXTNAME = 'SimMap_Sky' : Data columns
Column Name	Data Type	Units	Description
TEMPERATURE	Real*4	K_cmb (30-353 GHz) or MJy/sr (545 and 857 GHz)	The Stokes I map
Q-POLARISATION	Real*4	K_cmb (30-353 GHz)	The Stokes Q map (optional)
U-POLARISATION	Real*4	K_cmb (30-353 GHz)	The Stokes U map (optional)
Keyword	Data Type	Value	Description
PIXTYPE	string	HEALPIX
COORDSYS	string	GALACTIC	Coordinate system
ORDERING	string	NESTED	Healpix ordering
POLCCONV	String	COSMO	Polarization convention
NSIDE	Int	1024 or 2048	Healpix [math]N_{side}[/math]
FIRSTPIX	Int*4	0	First pixel number
LASTPIX	Int*4	12 [math]N_{side}[/math]2 – 1	Last pixel number

Note: Original PSM foreground components has been generated at NSIDE 2048 and using a gaussian beam of 4 arcmin. LFI CMB maps has been downgraded at NSIDE 1024.

CMB MC

There are 1000 realizations of the lensed CMB per frequency for FFP8 and FFP9, making a total of 18000 CMB simulations available in the PLA. They are named:

• HFI_SimMap_cmb-ffp8-scl-{nnnn}_2048_R2.00_nominal.fits
• LFI_SimMap_cmb-ffp8-scl-{nnnn}_1024_R2.00_nominal.fits

• HFI_SimMap_cmb-ffp9-scl-{nnnn}_2048_R2.00_nominal.fits
• LFI_SimMap_cmb-ffp9-scl-{nnnn}_1024_R2.00_nominal.fits

where nnnn ranges from 0000 to 1000.

CMB FFP8 and FFP9 simulated maps file data structure

1. EXTNAME = 'SimMap_cmb-ffp?-scl' : Data columns
Column Name	Data Type	Units	Description
TEMPERATURE	Real*4	K_cmb (30-353 GHz) or MJy/sr (545 and 857 GHz)	The Stokes I map
Q-POLARISATION	Real*4	K_cmb (30-353 GHz)	The Stokes Q map (optional)
U-POLARISATION	Real*4	K_cmb (30-353 GHz)	The Stokes U map (optional)
Keyword	Data Type	Value	Description
PIXTYPE	string	HEALPIX
COORDSYS	string	GALACTIC	Coordinate system
ORDERING	string	RING	Healpix ordering
POLCCONV	String	COSMO	Polarization convention
NSIDE	Int	1024 or 2048	Healpix [math]N_{side}[/math]
FIRSTPIX	Int*4	0	First pixel number
LASTPIX	Int*4	12 [math]N_{side}[/math]2 – 1	Last pixel number

Noise MC

There are 1000 of the noise per frequency for FFP8, making 9000 noise realizations available in the PLA. They are named

• HFI_SimMap_noise-ffp8-{nnnn}_2048_R2.00_nominal.fits
• LFI_SimMap_noise-ffp8-{nnnn}_1024_R2.00_nominal.fits

where nnnn ranges from 0000 to 1000.

Noise simulated maps file data structure

1. EXTNAME = 'SimMap_Sky' : Data columns
Column Name	Data Type	Units	Description
TEMPERATURE	Real*4	K_cmb
Keyword	Data Type	Value	Description
PIXTYPE	string	HEALPIX
COORDSYS	string	GALACTIC	Coordinate system
ORDERING	string	NESTED	Healpix ordering
POLCCONV	String	COSMO	Polarization convention
NSIDE	Int	1024 or 2048	Healpix [math]N_{side}[/math]
FIRSTPIX	Int*4	0	First pixel number
LASTPIX	Int*4	12 [math]N_{side}[/math]2 – 1	Last pixel number

Lensing Simulations

The lensing simulations package contains 100 realisations of the Planck "MV (TT+TE+ET+TB+BT+EE+EB+BE)" lensing potential estimate (November 2014 pipeline v12), as well as the input lensing realizations. They can be used to determine error bars as well eas effective normalizations for cross-correlation with other tracers of lensing. These simulations are of the lensing convergence map contained in the Lensing map release file. The production and characterisation of this lensing potential map are described in detail in Planck-2015-A15, which also describes the procedure used to generate the realizations given here.

The simulations are delivered as a gzipped tarball of approximately 8 GB in size. For delivery purposes, the package has been split into 4 2GB files using the unix command

split -d -b 2048m

• http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.00
• http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.01
• http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.02
• http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.03

After downloading the individual chunks, the full tarball can be reconstructed with the command

cat COM_Lensing-SimMap_2048_R2.00.tar.* | tar xvf -

The contents of the tarball are described below:

Contents of COM_Lensing-SimMap_2048_R2.00.tar

Filename	Format	Description
obs_klms/sim_????_klm.fits	HEALPIX FITS format alm, with [math] L_{\rm max} = 2048 [/math]	Contains the simulated convergence estimate [math] \hat{\kappa}_{LM} = \frac{1}{2} L(L+1)\hat{\phi}_{LM} [/math] for each simulation.
sky_klms/sim_????_klm.fits	HEALPIX FITS format alm, with [math] L_{\rm max} = 2048 [/math]	Contains the input lensing convergence for each simulation.
inputs/mask.fits.gz	HEALPIX FITS format map, with [math] N_{\rm side} = 2048 [/math]	Contains the lens reconstruction analysis mask.
inputs/cls/cl??.dat	ASCII text file, with columns = ([math]L[/math], [math]C_L [/math])	Contains the fiducial theory CMB power spectra for TT, EE, BB, [math] \kappa \kappa [/math] and [math] T \kappa [/math], with temperature and polarization in units of [math] \mu K [/math].

2013 Release of simulated maps

Introduction

The 2013 Planck data release is supported by a set of simulated maps of the model sky, by astrophysical component, and of that sky as seen by Planck. The simulation process consists of

1. modeling each astrophysical component of the sky emission for each Planck detector, using pre-Planck data and the relevant characteristics of the Planck instruments (namely the detector plus filter transmissions curves).
2. simulating each detector's observation of each sky component following the Planck scanning strategy and using the best estimates of the detector's beam and noise properties (now obtained in flight), then combining these timelines into a single one per detector, and projecting these simulated timelines onto observed maps (the fiducial sky), as is done with the on-orbit data;
3. generating Monte Carlo realizations of the CMB and of the noise, again following the Planck scanning strategy and using our best estimates of the detector beams and noise properties respectively.

The first step is performed by the Planck Sky Model (PSM), and the last two by the Planck Simulation Tools (PST), both of which are described in the sections below.

The production of a full focal plane (FFP) simulation, and including the many MC realizations of the CMB and the noise, requires both HFI and LFI data and includes large, computationally challenging, MC realizations. They are too large to be generated on either of the DPC's own cluster. Instead the PST consists of three distinct tools, each designed to run on the largest available supercomputers, that are used to generate the fiducial sky realization, the CMB MC, and the noise MC respectively. The simulations delivered here are part of the 6th generation FFP simulations, known as FFP6. They were primarily generated on the Hopper and Edison systems at NERSC, with some of the LFI noise MCs generated on the Louhi system at CSC.

While FFP6 includes our best measurements of the detector band-passes, main beams and noise power spectral densities, and is guaranteed to be internally self-consistent, there are a number of differences with the real data that should be borne in mind, although all tests performed to date indicate that these are statistically insignificant:

• the beams do not include far side-lobes;
• the detector noise characteristics are assumed stable: a single noise spectrum per detector is used for the entire mission;
• it assumes perfect calibration, transfer function deconvolution and deglitching;
• it uses the HFI pointing solution for the LFI frequencies, rather than the DPC's two focal plane model.
• it uses a different map-maker to HFI, and as a consequence implements very slightly different data cuts - primarily at ring boundaries - resulting in marginally different hit-maps.

The Planck Sky Model

Overall description

The Planck Sky Model, PSM, consists of a set of data and of code used to simulate sky emission at millimeter-wave frequencies; it is described in detail in Delabrouille et al., (2013), henceforth the PSM paper..

The Planck Sky Model is available here: http://www.apc.univ-paris7.fr/~delabrou/PSM/psm.html

The main simulations used to test and validate the Planck data analysis pipelines (and, in particular, component separation) makes use of simulations generated with version 1.7.7 of the PSM software. The total sky emission is built from the CMB plus ten foreground components, namely thermal dust, spinning dust, synchrotron, CO lines, free-free, thermal Sunyaev-Zel'dovich (SZ) effect (with first order relativistic corrections), kinetic SZ effect, radio and infrared sources, Cosmic Infrared Background (CIB).

The CMB is modeled using CAMB. It is based on adiabatic initial perturbations, with the following cosmological parameters:

• T_CMB = 2.725
• H = 0.684
• OMEGA_M = 0.292
• OMEGA_B = 0.04724
• OMEGA_NU = 0
• OMEGA_K = 0
• SIGMA_8 = 0.789
• N_S = 0.9732
• N_S_RUNNING = 0
• N_T = 0
• R = 0.0844
• TAU_REION = 0.085
• HE_FRACTION = 0.245
• N_MASSLESS_NU = 3.04
• N_MASSIVE_NU = 0
• W_DARK_ENERGY = -1
• K_PIVOT = 0.002
• SCALAR_AMPLITUDE = 2.441e-9

and all other parameters are set to the default standard of the Jan 2012 version of CAMB. In addition, this simulated CMB contains non-Gaussian corrections of the local type, with an f_NL parameter of 20.4075.

The Galactic ISM emission comprises five components: thermal dust, spinning dust, synchrotron, CO lines, and free-free emission. We refer the reader to the PSM publication for details. For the simulations generated here, however, the thermal dust model has been modified in the following way: instead of being based on the 100 micron map of Schlegel, Finkbeiner and Davis (2008), henceforth SFB, the dust template uses an internal release of the 857 GHz Planck observed map itself, in which point sources have been subtracted, and which has been locally filtered to remove CIB fluctuations in the regions of lowest column density. A caveat is that while this reduces the level of CIB fluctuations in the dust map in some of the regions, in regions of moderate dust column density the CIB contamination is actually somewhat larger than in the SFD map (by reason of different emission laws for dust and CIB, and of the higher resolution of the Planck map).

The other emissions of the galactic ISM are simulated using the prescription described in the PSM paper. Synchrotron, free-free and spinning dust emission are based on WMAP observations, as analyzed by Miville-Deschenes et al. (2008). Small scale fluctuations have been added to increase the variance on small scales and compensate the lower resolution of WMAP as compared to Planck (in particular for the HFI channels). The main limitation of these maps is the presence at high galactic latitude of fluctuations that may be attributed to WMAP noise. The presence of noise and of added Gaussian fluctuations on small scales may result in a few occasional pixels being negative (e.g. in the spinning dust maps). Low frequency foreground maps are also contaminated by some residuals of bright radio sources that have not been properly subtracted from the templates of diffuse emission.

The CO maps are simulated using the CO J=1-0 observations of Dame et al. (2001). The main limitations are limited sky coverage, lower resolution than that of Planck high frequency channels, line ratios (J=2-1)/(J=1-0) and (J=3-2)/(J=2-1) constant over the sky. The CO in the simulation is limited to the three lowest ¹²CO lines. No CO maps has been simulated at the LFI frequnecy (30, 44 and 70 GHz).

Galaxy clusters are generated on the basis of cluster number counts, following the Tinker et al. (2008) mass function, for the cosmological parameters listed above. Clusters are assumed perfectly spherical, isothermal, and are modeled using the universal pressure profile of Arnaud et al. (2010). Relativistic corrections following Itoh et al. (1998) are included to first order. The simulated kinetic SZ effect assumes no bulk flow, and a redshift-dependent average cluster velocity compatible with the linear growth of structures.

Point sources comprise radio sources (based on extrapolations across frequencies of radio observations between 800 MHz and 5 GHz) and infrared sources (based on extrapolations in frequencies of IRAS sources). One caveat is that due to the unevenness of the radio source surveys, the equatorial southern part of the sky has less faint radio sources than the northern part. Although all the missing sources are well below the Planck detection level, this induces a small variation of the total emission background over the sky. Check the individual faint point source emission maps if this is a potential problem for your applications. See also the PSM paper for details about the PSM point source simulations. The PSM separates bright and faint point source; the former are initially in a catalog, and the latter in a map, though a map of the former can also be produced. In the processing below, the bright sources are simulated via the catalog, but for convenience they are delivered as a map.

Finally, the far infrared background due to high redshift galaxies has been simulated using a procedure is based on the distribution of galaxies in shells of density contrast at various redshifts (Castex et al., PhD thesis; paper in preparation). This simulation has been modified by gradually substituting an uncorrelated extra term of CIB emission at low frequencies, artificially added in particular to decorrelate the CIB at frequencies below 217 GHz from the CIB above that frequency, to mimic the apparent decorrelation observed in the Planck Early Paper on CIB power spectrum Planck-Early-XVIII.

While the PSM simulations described here provide a reasonably representative multi-component model of sky emission, users are warned that it has been put together mostly on the basis of data sets and knowledge pre-existing the Planck observations themselves. While it is sophisticated enough to include variations of emission laws of major components of the ISM emission, different emission laws for most sources, and a reasonably coherent global picture, it is not (and is not supposed to be) identical to the real sky emission. The users are warned to use these simulations with caution.

PSM Products

To build maps corresponding to the Planck channels, the models described above are convolved with the spectral response of the channel in question. The products given here are for the full frequency channels, and as such they are not used in the Planck specific simulations, which use only individual detector channels. The frequency channel spectral responses used (given in the RIMO), are averages of the responses of the detectors of each frequency channel weighted as they are in the mapmaking step. They are provided for the purpose of testing user's own software of simulations and component separation.

PSM maps of the CMB and of the ten foregrounds are given in the following map products:

HFI

• HFI_SimMap_cmb_2048_R1.10.fits
• HFI_SimMap_co_2048_R1.10.fits
• HFI_SimMap_firb_2048_R1.10.fits
• HFI_SimMap_strongps_2048_R1.10.fits
• HFI_SimMap_faintps_2048_R1.10.fits
• HFI_SimMap_freefree_2048_R1.10.fits
• HFI_SimMap_synchrotron_2048_R1.10.fits
• HFI_SimMap_thermaldust_2048_R1.10.fits
• HFI_SimMap_spindust_2048_R1.10.fits
• HFI_SimMap_kineticsz_2048_R1.10.fits
• HFI_SimMap_thermalsz_2048_R1.10.fits

LFI

• LFI_SimMap_cmb_1024_R1.10.fits
• LFI_SimMap_firb_1024_R1.10.fits
• LFI_SimMap_strongps_1024_R1.10.fits
• LFI_SimMap_faintps_1024_R1.10.fits
• LFI_SimMap_freefree_1024_R1.10.fits
• LFI_SimMap_synchrotron_1024_R1.10.fits
• LFI_SimMap_thermaldust_1024_R1.10.fits
• LFI_SimMap_spindust_1024_R1.10.fits
• LFI_SimMap_kineticsz_1024_R1.10.fits
• LFI_SimMap_thermalsz_1024_R1.10.fits

Each file contains a single BINTABLE extension with either a single map (for the CMB file) or one map for each HFI/LFI frequency (for the foreground components). In the latter case the columns are named F030, F044 ,F070,F100, F143, … , F857. Units are microK_CMB for the CMB, K_CMB at 30, 44 and 70 GHz and MJy/sr for the others. The structure is given below for multi-column files.

Note: Original PSM foreground components has been generated at NSIDE 2048 and using a gaussian beam of 4 arcmin, LFI maps where then smoothed to LFI resolution (32.0, 27.0 and 13.0 arcmin for the 30, 44 and 70 GHz) and donwgraded at NSIDE 1024. LFI CMB maps has been smoothed at 13.0 arcmin (70 GHz resolution) and downgraded at NSIDE 1024.

HFI FITS file structure

1. EXTNAME = 'SIM-MAP' : Data columns
Column Name	Data Type	Units	Description
F100	Real*4	K_CMB	100GHz signal map
F143	Real*4	K_CMB	143GHz signal map
F217	Real*4	K_CMB	217GHz signal map
F353	Real*4	K_CMB	353GHz signal map
F545	Real*4	MJy/sr	545GHz signal map
F857	Real*4	MJy/sr	857GHz signal map
Keyword	Data Type	Value	Description
PIXTYPE	string	HEALPIX
COMP	string	component	Astrophysical omponent
COORDSYS	string	GALACTIC	Coordinate system
ORDERING	string	NESTED	Healpix ordering
NSIDE	Int	2048	Healpix Nside for LFI and HFI, respectively
FIRSTPIX	Int*4	0	First pixel number
LASTPIX	Int*4	50331647	Last pixel number, for LFI and HFI, respectively
BAD_DATA	Real*4	-1.63750E+30	Healpix bad pixel value
BEAMTYPE	string	GAUSSIAN	Type of beam
BEAMSIZE	Real*4	size	Beam size in arcmin
PSM-VERS	string		PSM Versions used

LFI FITS file structure

1. EXTNAME = 'SIM-MAP' : Data columns
Column Name	Data Type	Units	Description
F030	Real*4	KCMB	30GHz signal map
F044	Real*4	KCMB	44GHz signal map
F070	Real*4	KCMB	70GHz signal map
Keyword	Data Type	Value	Description
PIXTYPE	string	HEALPIX
COMP	string	component	Astrophysical omponent
COORDSYS	string	GALACTIC	Coordinate system
ORDERING	string	NESTED	Healpix ordering
NSIDE	Int	1024	Healpix Nside for LFI and HFI, respectively
FIRSTPIX	Int*4	0	First pixel number
LASTPIX	Int*4	12582911	Last pixel number, for LFI and HFI, respectively
BAD_DATA	Real*4	-1.63750E+30	Healpix bad pixel value
BEAMTYPE	string	GAUSSIAN	Type of beam
BEAMS_30	Real*4	32.0	Beam size at 30 GHz in arcmin
BEAMS_44	Real*4	27.0	Beam size at 44 GHz in arcmin
BEAMS_70	Real*4	13.0	Beam size at 70 GHz in arcmin
PSM-VERS	string		PSM Versions used

The Fiducial Sky Simulations

For each detector, fiducial time-ordered data are generated separately for each of the ten PSM components using the LevelS software as follows:

• the detector's beam and PSM map are converted to spherical harmonics using beam2alm and anafast respectively;
• the beam-convolved map value is calculated over a 3-dimensional grid of sky locations and beam orientations using conviqt;
• the map-based timelines are calculated sample-by-sample by interpolating over this grid using multimod;
• the catalogue-based timelines are produced sample-by-sample by beam-convolving any point source laying within a given angular distance of the pointing at each sample time using multimod.

For each frequency, fiducial sky maps are generated for

• the total signal (i.e. sky + instrument noise), for both the nominal mission and the halfrings thereof (see details)
• the foreground sky alone (excluding CMB but including noise),
• the point source sky, and
• the noise alone

All maps are built using the MADAM destriping map-maker interfaced with the TOAST data abstraction layer . In order to construct the total timelines required by each map, for each detector TOAST reads the various component timelines separately and sums then, and, where necessary, simulates and adds a noise realization time-stream on the fly. HFI frequencies are mapped at HEALPix resolution Nside=2048 using ring-length destriping baselines, while LFI frequencies are mapped at Nside=1024 using 1s baselines.

Products delivered

A single simulation is delivered, which is divided into two types of products:

1. six files of the full sky signal at each HFI and LFI frequency, and their corresponding halfring maps:

HFI_SimMap_100_2048_R1.10_nominal.fits	HFI_SimMap_100_2048_R1.10_nominal_ringhalf_1.fits	HFI_SimMap_100_2048_R1.10_nominal_ringhalf_2.fits
HFI_SimMap_143_2048_R1.10_nominal.fits	HFI_SimMap_143_2048_R1.10_nominal_ringhalf_1.fits	HFI_SimMap_143_2048_R1.10_nominal_ringhalf_2.fits
HFI_SimMap_217_2048_R1.10_nominal.fits	HFI_SimMap_217_2048_R1.10_nominal_ringhalf_1.fits	HFI_SimMap_217_2048_R1.10_nominal_ringhalf_2.fits
HFI_SimMap_353_2048_R1.10_nominal.fits	HFI_SimMap_353_2048_R1.10_nominal_ringhalf_1.fits	HFI_SimMap_353_2048_R1.10_nominal_ringhalf_2.fits
HFI_SimMap_545_2048_R1.10_nominal.fits	HFI_SimMap_545_2048_R1.10_nominal_ringhalf_1.fits	HFI_SimMap_545_2048_R1.10_nominal_ringhalf_2.fits
HFI_SimMap_857_2048_R1.10_nominal.fits	HFI_SimMap_857_2048_R1.10_nominal_ringhalf_1.fits	HFI_SimMap_857_2048_R1.10_nominal_ringhalf_2.fits

LFI_SimMap_030_1024_R1.10_nominal.fits	LFI_SimMap_030_1024_R1.10_nominal_ringhalf_1.fits	LFI_SimMap_030_1024_R1.10_nominal_ringhalf_2.fits
LFI_SimMap_044_1024_R1.10_nominal.fits	LFI_SimMap_044_1024_R1.10_nominal_ringhalf_1.fits	LFI_SimMap_044_1024_R1.10_nominal_ringhalf_2.fits
LFI_SimMap_070_1024_R1.10_nominal.fits	LFI_SimMap_070_1024_R1.10_nominal_ringhalf_1.fits	LFI_SimMap_070_1024_R1.10_nominal_ringhalf_2.fits

These files have the same structure as the equivalent SkyMap products described in the Frequency Maps chapter, namely one BINTABLE extension with three columns containing 1) Signal, 2) hit-count, and 3) variance. Units are K_CMB for all channels.

2. Three files containing 1) the sum of all astrophysical foregrounds, 2) the point sources alone, and 3) the noise alone: which are subproducts of the above, and are in the form of the PSM maps described in the previous section.

• HFI_SimMap_foreground_2048_R1.10_nominal.fits
• HFI_SimMap_noise_2048_R1.10_nominal.fits
• HFI_SimMap_ps_2048_R1.10_nominal.fits

• LFI_SimMap_foreground_1024_R1.10_nominal.fits
• LFI_SimMap_noise_1024_R1.10_nominal.fits
• LFI_SimMap_ps_1024_R1.10_nominal.fits

These files have the same structure as the PSM output maps described above, namely a single BINTABLE extension with 6 columns named F100 -- F857 each containing the given map for that HFI band and with 3 columns named F030, F044, F070 each containing the given map for that LFI band. Units are alway K_CMB.

Note that the CMB alone is not delivered as a separate product, but it can be recovered by simple subtraction of the component maps for the total signal map.

Monte Carlo realizations of CMB and of noise

The CMB MC set is generated using FEBeCoP, which generates an effective beam for each pixel in a map at each frequency by accumulating the weights of all pixels within a fixed distance of that pixel, summed over all observations by all detectors at that frequency. It then applies this effective beam pixel-by-pixel to each of 1000 input CMB sky realizations.

The noise MC set is generated just as the fiducial noise maps, using MADAM/TOAST. In order to avoid spurious correlations within and between the 1000 realizations, each stationary interval for each detector for each realization is generated from a distinct sub-sequence of a single statistically robust, extremely long period, pseudo-random number sequence.

Products delivered

100 realizations of the CMB (lensed) and of the noise are made available. They are named

• HFI_SimMap_cmb-{nnnn}_2048_R1.nn_nominal.fits
• HFI_SimMap_noise-{nnnn}_2048_R1.nn_nominal.fits
• LFI_SimMap_cmb-{nnnn}_2048_R1.nn_nominal.fits
• LFI_SimMap_noise-{nnnn}_2048_R1.nn_nominal.fits

where nnnn ranges from 0000 to 0099.

The FITS file structure is the same as for the other similar products above, with a single BINTABLE extension with six columns, one for each HFI frequency, named F100, F143, … , F857 and with three columns, one for each LFI frequency, named F030, F044, F070. Units are always microK_CMB(NB: due to an error in the HFI file construction, the unit keywords in the headers indicate K_CMB, the "micro" is missing there).

Lensing Simulations

N.B. The information in this section is adapted from the package Readme.txt file.

The lensing simulations package contains 100 realisations of the Planck 2013 "MV" lensing potential estimate, as well as the input CMB and lensing potential [math]\phi[/math] realizations. They can be used to determine error bars for cross-correlations with other tracers of lensing. These simulations are of the PHIBAR map contained in the Lensing map release file. The production and characterisation of this lensing potential map are described in detail in Planck-2013-XVII, which describes also the procedure used to generate the realizations given here.

Products delivered

The simulations are delivered as a single tarball of ~17 GB containing the following directories:

obs_plms/dat_plmbar.fits - contains the multipoles of the PHIBAR map in COM_CompMap_Lensing_2048_R1.10.fits

obs_plms/sim_????_plmbar.fits - simulated relizations of PHIBAR, in Alm format.

sky_plms/sim_????_plm.fits - the input multipoles of phi for each simulation

sky_cmbs/sim_????_tlm_unlensed.fits - the input unlensed CMB multipoles for each simulation

sky_cmbs/sim_????_tlm_lensed.fits - the input lensed CMB multipoles for each simulation.

inputs/cls/cltt.dat - Fiducial lensed CMB temperature power spectrum C_l^TT.

inputs/cls/clpp.dat - Fiducial CMB lensing potential power spectrum C_l^PP.

inputs/cls/cltp.dat - Fiducial correlation between lensed T and P.

inputs/cls/cltt_unlensed.dat - Fiducial unlensed CMB temperature power spectrum.

inputs/filt_mask.fits.gz - HEALpix Nside=2048 map containing the analysis mask for the lens reconstructions (equivalent to the MASK column in COM_CompMap_Lensing_2048_R1.10.fits)

All of the .fits files in this package are HEALPix Alm, to lmax=2048 unless otherwise specified.

For delivery purposes this package has been split into 2 GB chunks using the unix command

split -d -b 2048m

which produced files with names like COM_SimMap_Lensing_R1.10.tar.nn, with nn=00-07. They can be recombined and the maps extracted via

cat COM_SimMap_Lensing_R1.10.tar.* | tar xvf -