Simulations
Contents
[hide]- 1 Introduction
- 2 The end-to-end simulation pipeline
- 3 Delivered Products
- 4 Two important warnings about noise and thermal dust
- 5 References
- 6 Other Releases: 2020-NPIPE, 2015 and 2013 simulated maps
- 7 References
Introduction[edit]
While PR2-2015 simulations (FFP8[1]) were focused on the reproduction of the flight data Gaussian noise power spectra and their time variations, this new PR3-2018 simulation (FFP10) brings for the first time the realistic simulation of instrumental effects for both HFI and LFI. Moreover these simulated systematic effects are processed in the timelines with the same algorithms (and when possible, codes) as for the flight data.
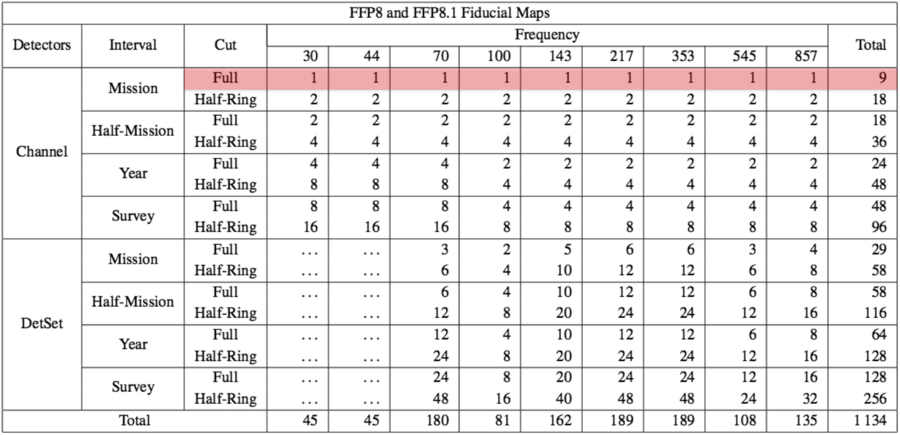
The FFP10 dataset is made of several full-sky map sets in FITS format:
- 1000 realizations of lensed scalar CMB convolved with effective beams per HFI frequency,
- separated input sky components per HFI bolometer and LFI radiometer
- 300 realizations of noise and systematic effect residuals per frequency,
- one fiducial simulation with full sky signal components: lensed scalar CMB, foregrounds, noise and systematic effect residuals, for all frequencies,
The end-to-end simulation pipeline[edit]
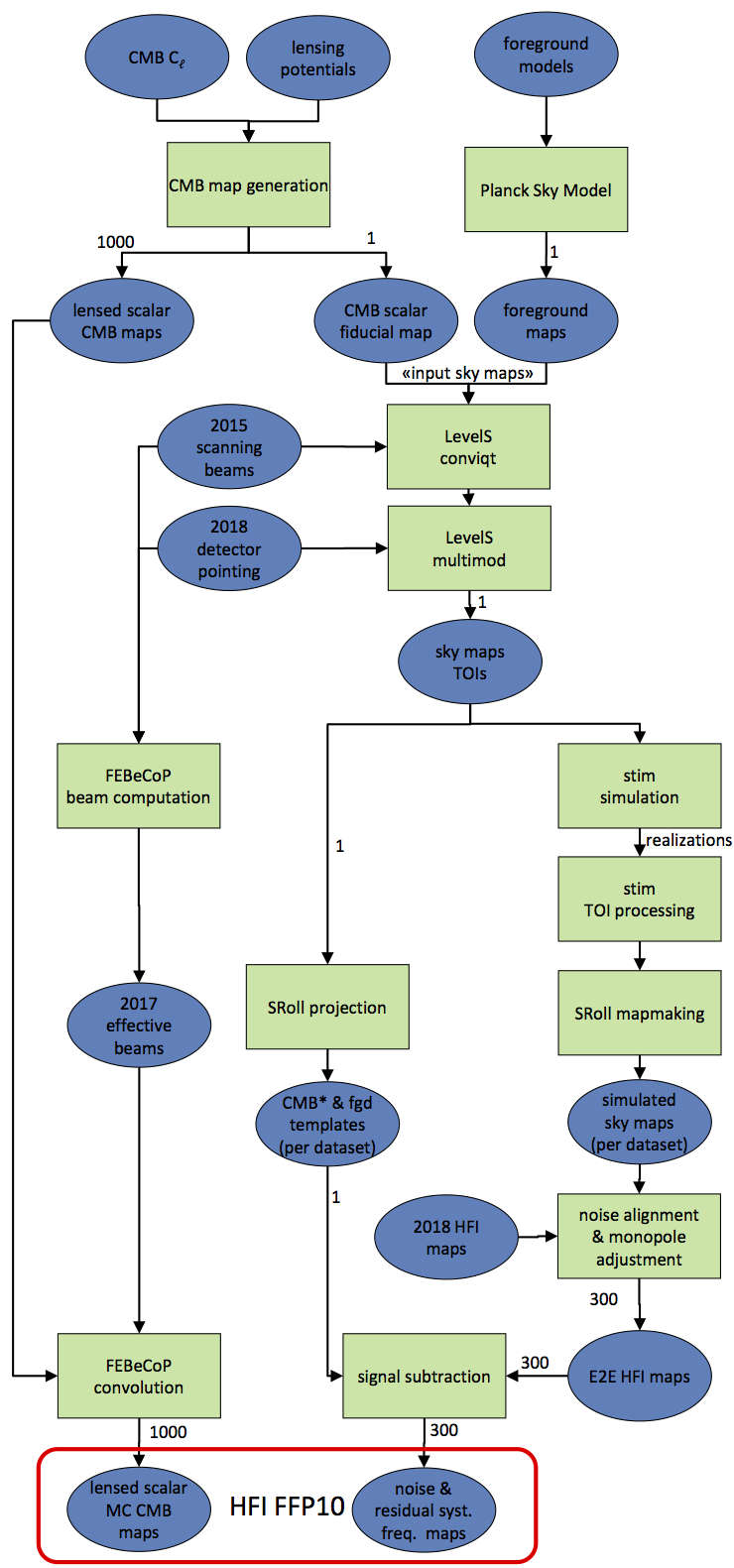
The end-to-end simulation pipeline uses several software components which are described below in the order they are used, as seen in the following schematic. Note that while this schematic is specific to HFI, the main components in the block diagram are similar for both instruments.
Please note that most of what is written here comes from Planck-2020-A3[2], which reading is highly recommended for more precisions on technical details and plots, particularly about the characterization of the negligible effects and systematics.
CMB[edit]
The FFP10 lensed CMB maps are generated in the same way as for the previous FFP8 release and described in detail in Planck-2015-A12[1]. FFP10 simulations only contain the scalar part lensed with independent lensing potential realizations.
One "fiducial" realization is used as input CMB for the full end-to-end pipeline, and 1000 other realizations are convolved with FEBeCoP[3] effective beams to be combined with the 300 noise and systematic residuals maps.
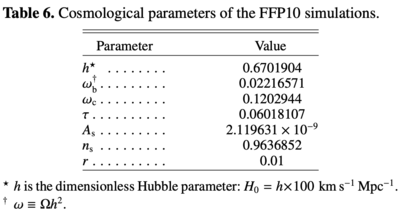
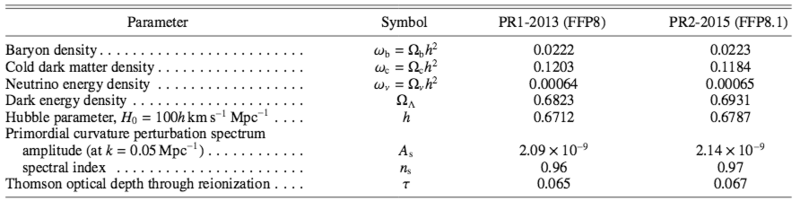
The cosmological parameters used are:
| Parameter | Symbol | FFP8.1 | FFP10 |
|---|---|---|---|
| Baryon density | |||
| Cold dark matter density | |||
| Neutrino energy density | |||
| Hubble parameter, | |||
| Thomson optical depth through reionization | |||
| Primordial curvature perturbation spectrum: | |||
| amplitude | |||
| spectral index | |||
The Planck Sky Model[edit]
The FFP10 simulation input sky is the coaddition of the following sky components generated using the Planck Sky Model (PSM) package (Delabrouille et al. 2013 [4]). Each of these components is convovled with each HFI bolometer spectral response by the PSM software, using the same spectral responses as in 2015 FFP8. Please note that one important difference with FFP8 is that FFP10 PSM maps are not smoothed with any beam, while in FFP8 PSM maps were smoothed with a 5’ Gaussian beam.
Diffuse Galactic components[edit]
- Dust
The dust model maps are built as follows. The Stokes I map at 353 GHz is the dust total intensity Planck map obtained by applying the Generalized Needlet Internal Linear Combination (GNILC) method of Remazeilles et al. (2011)[5] to the PR2-2015 release of Planck HFI maps, as described in Planck-2016-XLVIII[6], and subtracting the monopole of the Cosmic Infrared Background (Planck-2015-A08[7]). For the Stokes Q and U maps at 353 GHz, we started with one realization of the statistical model of Vansyngel et al. (2017)[8]. The portions of the simulated Stokes Q and U maps near Galactic plane were replaced by the Planck 353-GHz PR2 data. The transition between data and simulation was made using a Galactic mask with a 5° apodization, which leaves 68% of the sky unmasked at high latitude. Furthermore, on the full sky, the large angular scales in the simulated Stokes Q and U maps were replaced by the Planck data. Specifically, the first ten multipoles came from the Planck 353-GHz PR2 data, while over the range, the simulations were introduced smoothly using the function .
To scale the dust Stokes maps from the 353-GHz templates to other Planck frequencies, we follow the FFP8 prescription (Planck-2015-A12[1]). A different modified blackbody emission law is used for each of the HEALPix pixels. The dust spectral index used for scaling in frequency is different for frequencies above and below 353 GHz. For frequencies above 353 GHz, the parameters come from the modified blackbody fit of the dust spectral energy distribution (SED) for total intensity obtained by applying the GNILC method to the PR2 HFI maps (Planck-2016-XLVIII[6]). These parameter maps have a variable angular resolution that decreases towards high Galactic latitudes. Below 353 GHz, we also use the dust temperature map from Planck-2016-XLVIII[6], but with a distinct map of spectral indices from Planck-2013-XI[9], which has an angular resolution of 30’. These maps introduce significant spectral variations over the sky at high Galactic latitudes, and between the dust SEDs for total intensity and polarization. The spatial variations of the dust SED for polarization in the FFP10 sky model are quantified in [ttps://www.aanda.org/articles/aa/abs/2018/11/aa32888-18/aa32888-18.html#page=1 Planck-2018-LIV][10].
- Synchrotron
Synchrotron intensity is modelled by scaling in frequency the 408-MHz template map from Haslam et al. (1982)[11], as reprocessed by Remazeilles et al. (2015)[12] using a single power law per pixel. The pixel-dependent spectral index is derived from an analysis of WMAP data by Miville-Deschênes et al. (2008)[13]. The generation of synchrotron polarization follows the prescription of Delabrouille et al. (2013)[4].
- Other components
Free-free, spinning dust models, and Galactic CO emissions are essentially the same as those used for the FFP8 sky model (Planck-2015-A12[1]), but the actual synchrotron and free-free maps used for FFP10 are obtained with a different realization of small-scale fluctuations of the intensity. CO maps do not include small-scale fluctuations, and are generated from the spectroscopic survey of Dame et al. (2001)[14]. None of these three components is polarized in the FFP10 simulations.
Unresolved point sources and cosmic infrared background[edit]
Catalogues of individual radio and low-redshift infrared sources are generated in the same way as for FFP8 simulations (Planck-2015-A12[1]), but use a different seed for random number generation. Number counts for three types of galaxies (early-type proto-spheroids, and more recent spiral and starburst galaxies) are based on the model of Cai et al. (2013)[15]. The entire Hubble volume out to redshift is cut into 64 spherical shells, and for each shell we generate a map of density contrast integrated along the line of sight between and , such that the statistics of these density contrast maps (i.e., power spectrum of linear density fluctuations, and cross-spectra between adjacent shells, as well as with the CMB lensing potential), obey statistics computed using the Cosmic Linear Anisotropy Solving System (CLASS) code (Blas et al. 2011[16]; Di Dio et al. 2013[17]). For each type of galaxy, a catalogue of randomly-generated galaxies is generated for each shell, following the appropriate number counts. These galaxies are then distributed in the shell to generate a single intensity map at a given reference frequency, which is scaled across frequencies using the prototype galaxy SED at the appropriate redshift.
Galaxy clusters[edit]
A full-sky catalogue of galaxy clusters is generated based on number counts following the method of Delabrouille et al. (2002)[18]. The mass function of Tinker et al. (2008)[19] is used to predict number counts. Clusters are distributed in redshift shells, proportionally to the density contrast in each pixel with a bias , in agreement with the linear bias model of Mo & White (1996)[20]. For each cluster, we assign a universal profile based on XMM observations, as described in Arnaud et al. (2010)[21]. Relativistic corrections are included to first order following the expansion of Nozawa et al. (1998)[22]. To assign an SZ flux to each cluster, we use a mass bias of to match actual cluster number counts observed by Planck for the best-fit cosmological model coming from CMB observations. We use the specific value .
The kinematic SZ effect is computed by assigning to each cluster a radial velocity that is randomly drawn from a centred Gaussian distribution, with a redshift-dependent standard deviation that is computed from the power spectrum of density fluctuations. This neglects correlations between cluster motions, such as bulk flows or pairwise velocities of nearby clusters.
Input sky maps to timelines[edit]
The LevelS software package (Reinecke et al. 2006 [23]) is used to convert the input sky maps to timelines for each bolometer.
- Using conviqtv3, the maps are convolved with the same scanning beams as for FFP8, which were produced by stacking intensity-only observations of planets (Planck-2015-A07[24], appendix B), and to which a fake polarization has been added using a simple model based on each bolometer polarization angle and leakage.
- The convolved maps are then scanned to timelines with multimod, using the same scanning strategy as the 2018 flight data release. The only difference between the 2018 scanning strategy and the 2015 one is that about 1000 stable pointing periods at the end of the mission are omitted in 2018, because it has been found that the data quality was significantly lower in this interval.
Instrument-specific simulations[edit]
The main new aspect of FFP10 is the production of End-to-end (E2E) detector simulations, which include all significant systematic effects, and are used to produce realistic maps of noise and systematic effect residuals.
HFI E2E simulations[edit]
The pipeline adds the modelled instrumental systematic effects at the timeline level. It includes noise only up to the time response convolution step, after which the signal is added and the systematics simulated. It was shown in appendix B.3.1 of Planck-2016-XLVI[25] that, including the CMB map in the inputs or adding it after mapmaking, leads to differences for the power spectra in CMB channels below the level. This justifies the use of CMB swapping even when non-Gaussian systematic effects dominate over the TOI detector noise.
Here are the main effects included in the FFP10 simulation:
- White noise: the noise is based on a physical model composed of photon, phonon, and electronic noises. The time-transfer functions are different for these three noise sources. A timeline of noise only is created, with the level adjusted to agree with the observed TOI white noise after removal of the sky signal averaged per ring.
- Bolometer signal time-response convolution: the photon white noise is convolved with the bolometer time response using the same code and same parameters as in the 2015 processing. A second white noise contribution is added to the convolved photon white noise to simulate the electronics noise.
- Noise auto-correlation due to deglitching: the deglitching step in the data processing creates noise auto-correlation by flagging samples that are synchronous with the sky. Since we do not simulate the cosmic-ray glitches, we mimic this behaviour by adjusting the noise of samples above a given threshold to simulate their flagging.
- Time response deconvolution: the timeline containing the photon and electronic noise contributions is then deconvolved with the bolometer time response and low-pass filtered to limit the amplification of the high-frequency noise, using the same parameters as in the 2015 data processing.
- The input sky signal timeline is added to the convolved/deconvolved noise timeline and is then put through the instrument simulation. Note that the sky signal is not convolved/deconvolved with the bolometer time response, since it is already convolved with the scanning beam extracted from the 2015 TOI processing output which already contains the low-pass filter and residuals associated with the time-response deconvolution.
- Simulation of the signal non-linearity: the first step of electronics simulation is the conversion of the input sky plus noise signal from KCMB units to analog-to-digital units (ADU) using the detector response measured on the ground and assumed to be stable in time. The ADU signal is then fed through a simulator of a non-linear analogue-to-digital converter (ADCNL). This step is the one introducing complexity into the signal, inducing time variation of the response, and causing gain differences with respect to the ground-based measurements. This corresponds to specific new correction steps in the mapmaking.
- The ADCNL transfer-function simulation is based on the TOI processing, with correction from the ground measurements, combined with in-flight measurements. A reference simulation is built for each bolometer, which minimizes the difference between the simulation and the data gain variations, measured in a first run of the mapmaking. Realizations of the ADCNL are then drawn to mimic the variable behaviour of the gains seen in the 2018 data.
- Compression/decompression: the simulated signal is compressed by the algorithm required by the telemetry rate allocated to the HFI instrument, with a slight accuracy loss. While very close to the compression algorithm used on-board, the one used in the simulation pipeline differs slightly, due to the non-simulation of the cosmic-ray glitches, together with the use of the average of the signal in the compression slice.
- The same number of compression steps as in flight data, the signal mean of each compression slice and the step value for each sample are then used by the decompression algorithm to reconstruct the modulated signal.
TOI processing[edit]
The TOIs issued from the steps above are then processed in the same way as the flight data. Because of the granularity needed and the computational performance required to produce hundreds of realizations, the TOI processing pipeline applied to the simulated data is highly optimized and slightly different from the one used for the data. The specific steps are the following:
- ADCNL correction: the ADCNL correction is carried out with the same parameters as the 2015 data TOI processing, and with the same algorithm. The difference between the realizations of ADC transfer function used for simulation and the constant one used for TOI processing is tuned to reproduce the gain variations found in 2015 processed TOI.
- Demodulation: signal demodulation is also performed in the same way as the flight TOI processing. First, the signal is converted from ADU to volts. Next, the signal is demodulated by subtracting from each sample the average of the modulated signal over 1 hour and then taking the opposite value for "negative" parity samples.
- Conversion to watts and thermal baseline subtraction: the demodulated signal is converted from volts to watts (neglecting the conversion non-linearity of the bolometers and amplifiers, which has been shown to be negligible). Eventually, the flight data thermal baseline, derived from the deglitched signals of the two dark bolometers smoothed over 1 minute, is subtracted.
- 1/f noise: a 1/f type noise component is added to the signal for each stable pointing period, with parameters (slope and knee frequency) adjusted on the flight data.
- Projection to HPR: the signal timeline is then projected and binned to HEALPix pixels for each stable pointing period (HEALPix rings, or HPR) after removal of flight-flagged data (unstable pointing periods, glitches, Solar system objects, planets, etc.).
- 4-K line residuals: a HPR of the 4-K line residuals for each bolometer, built by stacking the 2015 TOI, is added to the simulation output HPR.
Effects and processings not simulated[edit]
- no discrete point sources,
- no glitching/deglitching, only deglitching-induced noise auto-correlation,
- no 4-K line simulation and removal, only addition of their residuals,
- no bolometer volts-to-watts conversion non-linearity from the bolometers and amplifiers,
- no far sidelobes (FSLs),
- reduced simulation pipeline at 545 GHz and 857 GHz
To be more specific about this last item, the submillimetre channels simulation uses a pipeline without electronics simulation. It only contains photon and electronic noises, deglitching noise auto-correlation, time-response convolution/deconvolution, and 1/f noise. Bolometer by bolometer baseline addition and thermal baseline subtraction, compression/decompression, and 4-K line residuals are not included.
Mapmaking[edit]
The next stage is to use the SRoll mapmaking on the stim HPR. The following mapmaking inputs are all the same for simulation as for flight data:
- thermal dust, CO, and free-free map templates,
- detector NEP and polarization parameters,
- detector pointings,
- bad ring lists and sample flagging
The FSL removal performed in the mapmaking destriper is not activated (since no FSL contribution is included in the input). The total dipole removed by the mapmaking is the same as the input in the sky TOIs generated by LevelS (given in section 4.2. of Planck-2020-A3[2]).
Post-processing[edit]
- Noise alignment: an additional noise component is added to more accurately align the noise levels of the simulations with the noise estimates built from the 2018 odd minus even ring maps. Of course, this adjustment of the noise level may not satisfy all the other noise null tests. This alignment is different for temperature and for polarization maps, in order to simulate the effect of the noise correlation between detectors within a PSB.
- Monopole adjustment: a constant value is added to each simulated map to bring its monopole to the same value as the corresponding 2018 map, which is described in section 3.1.1. of Planck-2020-A3[2].
- Signal subtraction: from each map, the input sky (CMB and foregrounds) is subtracted to build the “noise and residual systematics frequency maps.” These systematics include additional noise and residuals induced by sky-signal distortion. These maps are part of the FFP10 data set.
LFI E2E simulations[edit]
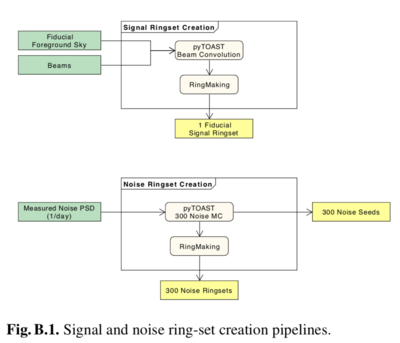
As described in Planck-2020-A2[26], the LFI systematic effect simulations are done partially at time- line and partially at ring-set level, with the goal of being as modular as possible, in order to create a reusable set of simulations. From the input sky model and according to the pointing information, we create single-channel ring-sets of the pure sky convolved with a suitable instrumental beam. To these we add pure noise (white and 1/ f ) ring-sets generated from the noise power spectrum distributions measured from real data one day at a time. The overall scheme is given in the Figure below:
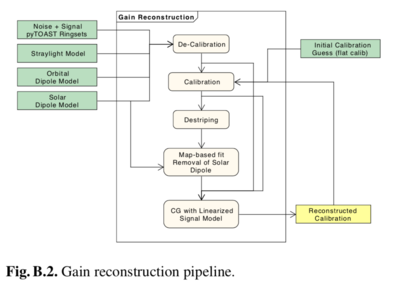
In the same manner, we create ring-sets for each of the specific systematic effects we would like to measure. We add together signal, noise, and systematic ring-sets, and, given models for straylight (based on the GRASP beams) and the orbital dipole, we create “perfectly-calibrated” ring-sets (i.e., calibration constant = 1). We use the gains estimate from the 2018 data release to “de-calibrate” these timelines, i.e., to convert them from kelvins to volts. At this point the calibration pipeline starts, and produces the reconstructed gains that will be different from the ones used in the de-calibration process due to the presence of simulated systematic effects. The calibration pipeline is algorithmically exactly the same as that used at the DPC for product creation, but with a different implementation (based principally on python). The gain-smoothing algorithm is the same as used for the data, and has been tuned to the actual data. This means that there will be cases where reconstructed gains from simulations differ significantly from the input ones. We have verified that this indeed happens, but only for very few pointing periods, and we therefore decided not to consider them in the following analysis. The overall process for estimating gains is given in the figure below:
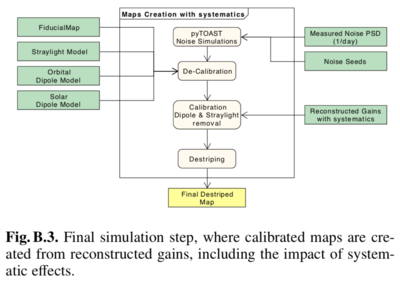
At this point we are able to generate maps for full mission, half-ring, and odd-even-year splits) that include the effects of systematic errors on calibration. In the final step, we produce timelines (which are never stored) starting from the same fiducial sky map, using the same model for straylight and the orbital dipole as in the previous steps, and from generated noise-only timelines created with the same seeds and noise model used before. We then apply the official gains to “de-calibrate” the timelines, which are immediately calibrated with the reconstructed gains in the previous step. The nominal destriping mapmaking algorithm is then used to create final maps. The complete data flow is given in the figure below:
Delivered Products[edit]
Input sky components[edit]
The separated input sky components generated by the Planck Sky Model are available for all frequencies, at HEALPix or or , depending on frequency:
| 100GHz | 143GHz | 217GHz | 353GHz | 545GHz | 857GHz | |
|---|---|---|---|---|---|---|
| fiducial lensed scalar CMB | ||||||
| CO | ||||||
| free-free | ||||||
| synchrotron | ||||||
| far infrared background | ||||||
| kinetic SZ | 100GHz kineticsz | 143GHz kineticsz | 217GHz kineticsz | 353GHz kineticsz | 545GHz kineticsz | 857GHz kineticsz |
| Thermal SZ | 100GHz thermalsz | 143GHz thermalsz | 217GHz thermalsz | 353GHz thermalsz | 545GHz thermalsz | 857GHz thermalsz |
| faint infrared point sources | 100GHz faintirps | 143GHz faintirps | 217GHz faintirps | 353GHz faintirps | 545GHz faintirps | 857GHz faintirps |
| faint radio point sources | 100GHz faintradiops | 143GHz faintradiops | 217GHz faintradiops | 353GHz faintradiops | 545GHz faintradiops | 857GHz faintradiops |
| thermal dust |
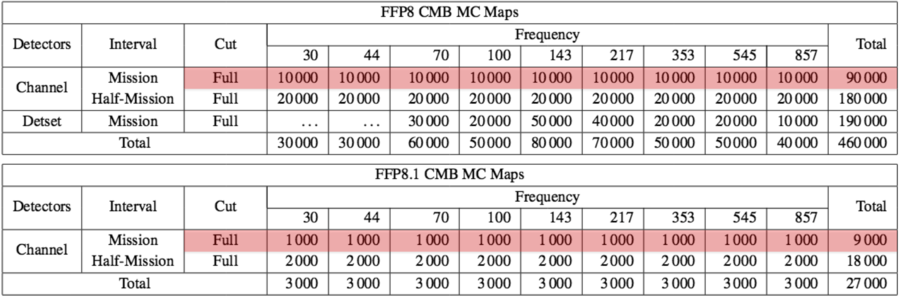
CMB realizations[edit]
The 1000 lensed scalar CMB map realizations are convolved with the FEBeCoP effective beams computed using the 2015 scanning beams (Planck-2015-A07[24], appendix B), and the updated scanning strategy described in the #PSM maps to timelines section above. Each CMB realization is available for the full-mission span only, at each frequency, which means 1000 realizations x 9 frequencies = 9000 CMB maps, which can be retrieved using the following link template:
http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=febecop_ffp10_lensed_scl_cmb_{frequency}_mc_{realization}.fits
where:
- {frequency} is any of frequency: 30, 44, 70, 100, 143, 217, 353, 545 or 857,
- {realization} is the realisation number, between 0000 and 0999, padded to four digits with leading zeros
For example: http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=febecop_ffp10_lensed_scl_cmb_100_mc_0000.fits
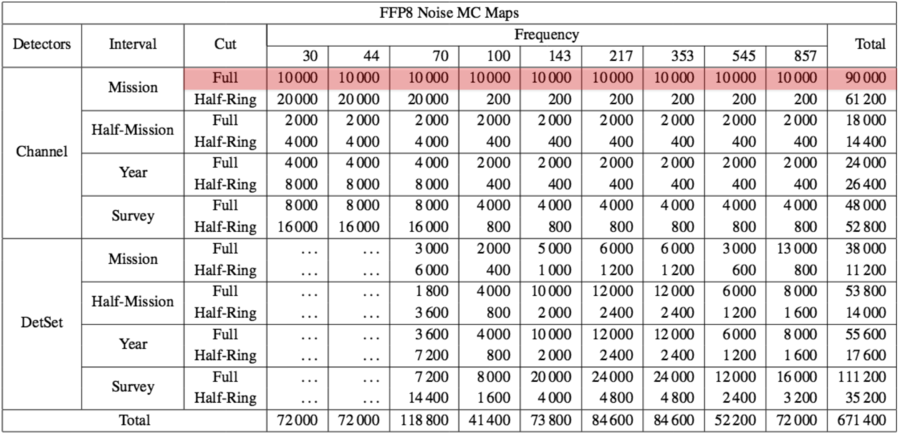
Noise and instrumental effect residual maps[edit]
HFI E2E maps[edit]
As described above, 300 realizations of full end-to-end simulations have been produced, to which the full sky signal part (CMB+foregrounds) have been subtracted in post-processing, to give maps of noise and systematic residuals only. For each realization and frequency, five data cuts are provided:
- full-mission,
- first and second half-missions,
- odd and even stable pointing periods (rings)
In addition to all 6 HFI frequencies, a special detector set made of only 353 GHz polarized bolometers (a.k.a 353_psb) is also published, to match the 2018 flight data set, for a total of 300 realizations x 5 data cuts x 7 HFI detector sets = 10,500 maps.
The noise maps can be retrieved from PLA using the following naming convention:
http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=ffp10_noise_{frequency}_{ring_cut}_map_mc_{realization}.fits
where:
- {frequency} is any of HFI frequency: 100, 143, 217, 353, 353_psb, 545 or 857,
- {ring_cut} is the ring selection scheme, one of: full, hm1, hm2, oe1, oe2
- {realization} is the realisation number, between 00000 and 00299, padded to five digits with leading zeros
For example: http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=ffp10_noise_100_full_map_mc_00000.fits
Please note that due to the specific polarization orientation of 100GHz bolometers, odd and even ring maps are badly conditionned for HEALPix and are therefore also available at by just replacing "_map_mc_" with "_map_1024_mc_" in the file link name.
LFI E2E maps[edit]
For LFI, a similar approach is followed as for HFI in terms of number and formatting of the E2E noise+systematics simulations.
Fiducial simulation[edit]
A separate full end-to-end simulation with a different CMB realization is also provided, with the full sky signal included and the same data cuts and detector sets as the 300 noise and systematic residual maps, to serve as a reference for whatever you would need it to. Please don't overlook the important warning below about thermal dust.
TODO: fiducial naming scheme
Two important warnings about noise and thermal dust[edit]
Noise[edit]
As stated in the introduction, FFP10 focus is on the simulation and correction of the main instrumental effects and systematics. It uses a noise model which doesn't vary in time, contrary to FFP8 simulations which used realizations of one noise power spectrum per stable pointing period and per detector. Doing so, all systematic residuals in FFP8 are considered as Gaussian noise, which time variations should follow the flight data.
If interested in Gaussian noise variations following flight data rather than non-Gaussian instrumental effects and systematic residuals, the user may want to check whether FFP8 noise maps better suit their needs. This is particularly true for 545 GHz and 857 GHz, for which FFP10 doesn't contain all instrumental effects and systematics and in which detectors' time response deconvolution is simulated at the noise-alignment post-processing step.
Thermal dust[edit]
After the production of the 300 realizations of noise and systematic residual simulations, a bug has been found in the PSM thermal dust template used as input, which led to a 10% intensity mismatch in temperature at 353 GHz due to a missing color correction. The same dust template has been correctly used for the simulations and for the sky subtraction post-processing, so the produced and published residual maps are not affected.
Note however, that the thermal dust maps provided as PSM input sky and the one used in the fiducial simulation are the fixed version of the PSM thermal dust, which slightly differs from the one used (and removed) in the 300 noise and systematic residual simulations.
References[edit]
- ↑ Jump up to: 1.01.11.21.31.4 Planck 2015 results. XII. Full Focal Plane Simulations, Planck Collaboration, 2016, A&A, 594, A12.
- ↑ Jump up to: 2.02.12.2 Planck 2018 results. III. High Frequency Instrument data processing and frequency maps, Planck Collaboration, 2020, A&A, 641, A3.
- Jump up ↑ Fast Pixel Space Convolution for Cosmic Microwave Background Surveys with Asymmetric Beams and Complex Scan Strategies: FEBeCoP, S. Mitra, G. Rocha, K. M. Górski, K. M. Huffenberger, H. K. Eriksen, M. A. J. Ashdown, C. R. Lawrence, ApJS, 193, 5-+, (2011).
- ↑ Jump up to: 4.04.1 The pre-launch Planck Sky Model: a model of sky emission at submillimetre to centimetre wavelengths, J. Delabrouille, M. Betoule, J.-B. Melin, M.-A. Miville-Deschênes, J. Gonzalez-Nuevo, M. Le Jeune, G. Castex, G. de Zotti, S. Basak, M. Ashdown, J. Aumont, C. Baccigalupi, A. Banday, J.-P. Bernard, F. R. Bouchet, D. L. Clements, A. da Silva, C. Dickinson, F. Dodu, K. Dolag, F. Elsner, L. Fauvet, G. Faÿ, G. Giardino, S. Leach, J. Lesgourgues, M. Liguori, J. F. Macias-Perez, M. Massardi, S. Matarrese, P. Mazzotta, L. Montier, S. Mottet, R. Paladini, B. Partridge, R. Piffaretti, G. Prezeau, S. Prunet, S. Ricciardi, M. Roman, B. Schaefer, L. Toffolatti, A&A, 553, A96, (2013).
- Jump up ↑ Foreground component separation with generalized Internal Linear Combination, Remazeilles, M. and Delabrouille, J. and Cardoso, J.-F., MNRAS, 418, 467, (2011).
- ↑ Jump up to: 6.06.16.2 Planck intermediate results. XLVIII. Disentangling Galactic dust emission and cosmic infrared background anisotropies, Planck Collaboration Int. XLVIII A&A, 596, A109, (2016).
- Jump up ↑ Planck 2015 results. VIII. High Frequency Instrument data processing: Calibration and maps, Planck Collaboration, 2016, A&A, 594, A8.
- Jump up ↑ Statistical simulations of the dust foreground to cosmic microwave background polarization, Vansyngel, F., Boulanger, F., Ghosh, T., et al., A&A, 603, A62, (2017).
- Jump up ↑ Planck 2013 results. XII. All-sky model of thermal dust emission, Planck Collaboration, 2014, A&A, 571, A12.
- Jump up ↑ Planck intermediate results. LIV. The Planck Multi-frequency Catalogue of Non-thermal Sources, Planck Collaboration Int. LIV, A&A, 619, A94, 2018
- Jump up ↑ A 408 MHz all-sky continuum survey. II - The atlas of contour maps, C. G. T. Haslam, H. Stoffel, C. J. Salter, W. E. Wilson, Astronomy and Astrophysics Supplement Series, 47, 1, (1982).
- Jump up ↑ An improved source-subtracted and destriped 408-MHz all-sky map, Remazeilles, M., Dickinson, C., Banday, A. J., Bigot-Sazy, M.-A., & Ghosh, T., MNRAS, 451, 4311, (2015).
- Jump up ↑ Separation of anomalous and synchrotron emissions using WMAP polarization data, M.-A. Deschênes, N. Ysard, A. Lavabre, N. Ponthieu, J. F. Macías-Pérez, J. Aumont, J. P. Bernard, A&A, 490, 1093-1102, (2008).
- Jump up ↑ The Milky Way in Molecular Clouds: A New Complete CO Survey, T. M. Dame, D. Hartmann, P. Thaddeus, ApJ, 547, 792-813, (2001).
- Jump up ↑ A Hybrid Model for the Evolution of Galaxies and Active Galactic Nuclei in the Infrared, Cai, Z.-Y., Lapi, A., Xia, J.-Q., et al., ApJ, 768, 21, (2013).
- Jump up ↑ The Cosmic Linear Anisotropy Solving System (CLASS). Part II: Approximation schemes, Blas, D., Lesgourgues, J., & Tram, T., J. Cosmology Astropart. Phys., 7, 034, (2011).
- Jump up ↑ The CLASSgal code for relativistic cosmological large scale structure, Di Dio, E., Montanari, F., Lesgourgues, J., & Durrer, R., J. Cosmology Astropart. Phys., 11, 044, (2013).
- Jump up ↑ AMiBA 2001: High-Z Clusters, Missing Baryons, and CMB Polarization, Delabrouille, J., Melin, J.-B., & Bartlett, J. G., Astronomical Society of the Pacific Conference Series, Vol. 257, (2002).
- Jump up ↑ Toward a Halo Mass Function for Precision Cosmology: The Limits of Universality, J. Tinker, A. V. Kravtsov, A. Klypin, K. Abazajian, M. Warren, G. Yepes, S. Gottlöber, D. E. Holz, ApJ, 688, 709-728, (2008).
- Jump up ↑ An analytic model for the spatial clustering of dark matter haloes, Mo, H. J. & White, S. D. M., MNRAS, 282, 347, (1996).
- Jump up ↑ The universal galaxy cluster pressure profile from a representative sample of nearby systems (REXCESS) and the Y_SZ - M_500 relation, M. Arnaud, G. W. Pratt, R. Piffaretti, H. Böhringer, J. H. Croston, E. Pointecouteau, ApJ, 517, A92, (2010).
- Jump up ↑ Relativistic Corrections to the Sunyaev-Zeldovich Effect for Clusters of Galaxies. II. Inclusion of Peculiar Velocities, S. Nozawa, N. Itoh, Y. Kohyama, ApJ, 508, 17-24, (1998).
- Jump up ↑ A simulation pipeline for the Planck mission, M. Reinecke, K. Dolag, R. Hell, M. Bartelmann, T. A. Enßlin, A&A, 445, 373-373, (2006).
- ↑ Jump up to: 24.024.1 Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
- Jump up ↑ Planck intermediate results. XLVI. Reduction of large-scale systematic effects in HFI polarization maps and estimation of the reionization optical depth, Planck Collaboration Int. XLVI A&A, 596, A107, (2016).
- Jump up ↑ Planck 2018 results. II. Low Frequency Instrument data processing, Planck Collaboration, 2020, A&A, 641, A2.
Other Releases: 2020-NPIPE, 2015 and 2013 simulated maps[edit]
2020 Release of simulated maps (NPIPE)
2015 Release of simulated maps
2013 Release of simulated maps
References
- ↑ Jump up to: 1.001.011.021.031.041.051.061.071.081.091.101.111.12 Planck 2015 results. XII. Full Focal Plane Simulations, Planck Collaboration, 2016, A&A, 594, A12.
- ↑ Jump up to: 2.02.1 Planck 2015 results. II. LFI processing, Planck Collaboration, 2016, A&A, 594, A2.
- ↑ Jump up to: 3.03.13.23.33.4 Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
- Jump up ↑ Planck 2015 results. X. Diffuse component separation: Foreground maps, Planck Collaboration, 2016, A&A, 594, A10.
- ↑ Jump up to: 5.05.1 Planck 2015 results. IV. LFI beams and window functions, Planck Collaboration, 2016, A&A, 594, A4.
- Jump up ↑ Planck 2013 results. VI. High Frequency Instrument Data Processing, Planck Collaboration, 2014, A&A, 571, A6.
- Jump up ↑ Planck 2013 results. IX. HFI spectral response, Planck Collaboration, 2014, A&A, 571, A9.
- ↑ Jump up to: 8.08.1 The pre-launch Planck Sky Model: a model of sky emission at submillimetre to centimetre wavelengths, J. Delabrouille, M. Betoule, J.-B. Melin, M.-A. Miville-Deschênes, J. Gonzalez-Nuevo, M. Le Jeune, G. Castex, G. de Zotti, S. Basak, M. Ashdown, J. Aumont, C. Baccigalupi, A. Banday, J.-P. Bernard, F. R. Bouchet, D. L. Clements, A. da Silva, C. Dickinson, F. Dodu, K. Dolag, F. Elsner, L. Fauvet, G. Faÿ, G. Giardino, S. Leach, J. Lesgourgues, M. Liguori, J. F. Macias-Perez, M. Massardi, S. Matarrese, P. Mazzotta, L. Montier, S. Mottet, R. Paladini, B. Partridge, R. Piffaretti, G. Prezeau, S. Prunet, S. Ricciardi, M. Roman, B. Schaefer, L. Toffolatti, A&A, 553, A96, (2013).
- Jump up ↑ Planck 2013 results. XII. All-sky model of thermal dust emission, Planck Collaboration, 2014, A&A, 571, A12.
- Jump up ↑ Planck 2013 results. I. Overview of Products and Results, Planck Collaboration, 2014, A&A, 571, A1.
- Jump up ↑ Planck 2013 results. XXVII. Doppler boosting of the CMB: Eppur si muove, Planck Collaboration, 2014, A&A, 571, A27.
- Jump up ↑ Planck 2015 results. VIII. High Frequency Instrument data processing: Calibration and maps, Planck Collaboration, 2016, A&A, 594, A8.
- ↑ Jump up to: 13.013.1 Planck 2015 results. XXVI. The second Planck catalogue of compact sources, Planck Collaboration, 2016, A&A, 594, A26.
- Jump up ↑ Planck 2015 results. XXVII. The second Planck catalogue of Sunyaev-Zeldovich sources, Planck Collaboration, 2016, A&A, 594, A27.
- Jump up ↑ Planck 2015 results. XV. Gravitational Lensing, Planck Collaboration, 2016, A&A, 594, A15.
- Jump up ↑ Maps of Dust Infrared Emission for Use in Estimation of Reddening and Cosmic Microwave Background Radiation Foregrounds, D. J. Schlegel, D. P. Finkbeiner, M. Davis, ApJ, 500, 525-+, (1998).
- Jump up ↑ Separation of anomalous and synchrotron emissions using WMAP polarization data, M.-A. Deschênes, N. Ysard, A. Lavabre, N. Ponthieu, J. F. Macías-Pérez, J. Aumont, J. P. Bernard, A&A, 490, 1093-1102, (2008).
- Jump up ↑ The Milky Way in Molecular Clouds: A New Complete CO Survey, T. M. Dame, D. Hartmann, P. Thaddeus, ApJ, 547, 792-813, (2001).
- Jump up ↑ Toward a Halo Mass Function for Precision Cosmology: The Limits of Universality, J. Tinker, A. V. Kravtsov, A. Klypin, K. Abazajian, M. Warren, G. Yepes, S. Gottlöber, D. E. Holz, ApJ, 688, 709-728, (2008).
- Jump up ↑ The universal galaxy cluster pressure profile from a representative sample of nearby systems (REXCESS) and the Y_SZ - M_500 relation, M. Arnaud, G. W. Pratt, R. Piffaretti, H. Böhringer, J. H. Croston, E. Pointecouteau, ApJ, 517, A92, (2010).
- Jump up ↑ Relativistic Corrections to the Sunyaev-Zeldovich Effect for Clusters of Galaxies. II. Inclusion of Peculiar Velocities, S. Nozawa, N. Itoh, Y. Kohyama, ApJ, 508, 17-24, (1998).
- Jump up ↑ Planck early results. XVIII. The power spectrum of cosmic infrared background anisotropies, Planck Collaboration XVIII, A&A, 536, A18, (2011).
- Jump up ↑ A simulation pipeline for the Planck mission, M. Reinecke, K. Dolag, R. Hell, M. Bartelmann, T. A. Enßlin, A&A, 445, 373-373, (2006).
- Jump up ↑ Making cosmic microwave background temperature and polarization maps with MADAM, E. Keihänen, R. Keskitalo, H. Kurki-Suonio, T. Poutanen, A.-S. Sirviö, A&A, 510, A57+, (2010).
- Jump up ↑ Fast Pixel Space Convolution for Cosmic Microwave Background Surveys with Asymmetric Beams and Complex Scan Strategies: FEBeCoP, S. Mitra, G. Rocha, K. M. Górski, K. M. Huffenberger, H. K. Eriksen, M. A. J. Ashdown, C. R. Lawrence, ApJS, 193, 5-+, (2011).
- Jump up ↑ Planck 2013 results. XVII. Gravitational lensing by large-scale structure, Planck Collaboration, 2014, A&A, 571, A17.
(Planck) High Frequency Instrument
(Planck) Low Frequency Instrument
Flexible Image Transfer Specification
Cosmic Microwave background
Planck Sky Model
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
Sunyaev-Zel'dovich
analog to digital converter
Noise Equivalent Power
Data Processing Center
Planck Legacy Archive
Attitude History File
Early Release Compact Source Catalog
Full-Width-at-Half-Maximum