Difference between revisions of "Map-making"
| (48 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{DISPLAYTITLE:Mapmaking}} | + | {{DISPLAYTITLE:HFI Mapmaking and photometric calibration}} |
== Introduction == | == Introduction == | ||
| Line 5: | Line 5: | ||
* Procedures for the 2013 release is to be found in {{PlanckPapers|planck2013-p03}} and {{PlanckPapers|planck2013-p03b}} (see at the bottom of this page) | * Procedures for the 2013 release is to be found in {{PlanckPapers|planck2013-p03}} and {{PlanckPapers|planck2013-p03b}} (see at the bottom of this page) | ||
* Procedures for the 2015 release is to be found in {{PlanckPapers|planck2014-a09}} (see at the bottom of this page) | * Procedures for the 2015 release is to be found in {{PlanckPapers|planck2014-a09}} (see at the bottom of this page) | ||
| − | * In 2016, a new procedure called ''SRoll'' has been introduced to extract, from the sky, parameters for systematics important to the mapmapking. This is achieved through a generalized polarized | + | * In 2016, a new procedure called ''SRoll'' has been introduced to extract, from the sky, parameters for systematics important to the mapmapking. This is achieved through a generalized polarized destriper which uses the redundancy between detectors inside a frequency band. Systematic effects producing leakages from intensity to polarization contribute strongly to this determinations. This allowed for the first time the use of large scale polarized data and the extraction of the reionization parameter. The procedure and its results are described in {{PlanckPapers|planck2016-XLVI}}. |
* For the 2018 legacy release, the same ''SRoll'' procedure has been used to produce the frequency intensity and polarization maps. {{PlanckPapers|planck2016-l03}} fully describes the procedures, the products and their characterization. | * For the 2018 legacy release, the same ''SRoll'' procedure has been used to produce the frequency intensity and polarization maps. {{PlanckPapers|planck2016-l03}} fully describes the procedures, the products and their characterization. | ||
== ''SRoll'' global solution == | == ''SRoll'' global solution == | ||
| − | ===Inputs to | + | ===Inputs to ''SRoll''=== |
For the 2018 release, the TOI processing remains unchanged from the previous 2015 release (see [[TOI_processing|TOI processing]]). As mentionned, a small cut of in the data selection (1000 pointing periods) has been done at the end of the cryogenic mission. | For the 2018 release, the TOI processing remains unchanged from the previous 2015 release (see [[TOI_processing|TOI processing]]). As mentionned, a small cut of in the data selection (1000 pointing periods) has been done at the end of the cryogenic mission. | ||
=== ''SRoll'' scheme === | === ''SRoll'' scheme === | ||
| − | ''SRoll'' makes use of an extended destriper. Destriper methods have been used previously to remove baseline drifts from detector time streams, while making co-added maps of the data, by taking advantage of the redundancy in the scanning strategy. | + | ''SRoll'' makes use of an extended destriper. Destriper methods have been used previously to remove baseline drifts from detector time streams, while making co-added maps of the data, by taking advantage of the redundancy in the scanning strategy. ''SRoll'' is a generalized polarized destriper which, in addition, compares all the observations of the same sky pixel by the same detector with different polarization angles, as well as by different detectors within the same frequency band. It thus fits differences between instrument parameters that minimize the difference between all polarized observations of the same sky pixel in the same frequency band. It solves consistently for: |
* one offset for each pointing period, | * one offset for each pointing period, | ||
* an empirical transfer function adding to the correction already done in the TOI processing (time constants less than 3 seconds), covering time constants up to 30 seconds, | * an empirical transfer function adding to the correction already done in the TOI processing (time constants less than 3 seconds), covering time constants up to 30 seconds, | ||
* a CMB calibration mismatch between detectors, detected through the shift on the total kinetic dipole, between odd and even surveys, inducing leakage from intensity to polarization, | * a CMB calibration mismatch between detectors, detected through the shift on the total kinetic dipole, between odd and even surveys, inducing leakage from intensity to polarization, | ||
* a bandpass mismatch for foregrounds response due to color corrections with respect to the CMB calibration, also inducing leakage from intensity to polarization. This makes use of an input spatial template (2015 Planck component separation results) of each foreground, | * a bandpass mismatch for foregrounds response due to color corrections with respect to the CMB calibration, also inducing leakage from intensity to polarization. This makes use of an input spatial template (2015 Planck component separation results) of each foreground, | ||
| − | * the absolute calibration from the orbital dipole (the kinetic dipole associated with the | + | * the absolute calibration from the orbital dipole (the kinetic dipole associated with the Earth motion around the Sun) which does not project on the sky. |
| − | The destripper is only sensitive to differences between bolometer coefficients. | + | The destripper is only sensitive to differences between bolometer coefficients. Thus, the absolute average value of the parameters within a frequency band is taken imposing: |
* the sum of the offsets to be zero (no monopoles), | * the sum of the offsets to be zero (no monopoles), | ||
| − | * the average of the additional color corrections (for both dust and free-free emission) to be zero, thus keeping the same average as the one | + | * the average of the additional color corrections (for both dust and free-free emission) to be zero, thus keeping the same average as the ground-based one. |
. | . | ||
| − | === | + | === ''SRoll'' outputs === |
| − | + | 1. ''SRoll'' ouputs are frequency sky maps (hereafater called "primary frequency maps"). These include the Solar dipole signal (i.e. the kinetic dipole associated with the motion of the Solar system with respect to the CMB) which projects on the sky. Combining these primary maps allows to separate the different components, and extract the Solar dipole. | |
| − | |||
| − | |||
| − | |||
| − | + | 2. From these primary frequency maps, the ''Planck'' 2015 Solar dipole (d,l,b)= (3364.5 ± 2.0 μK, 264.00 ± 0.03°, 48.24 ± 0.02°) is then removed leading to the delivered [[#Frequency maps|'''PR3 HFI frequency maps''']]. | |
| + | 3. The HFI frequency maps, combined with the LFI ones, lead, thanks to component separation methods, to physical component maps: [[CMB_maps|'''CMB maps''']] and [[Foreground_maps|'''diffuse foregrounds maps''']]. | ||
| + | |||
| + | 4. Removing the CMB anisotropies and diffuse foreground component maps from the primary frequency maps leaves a Solar dipole signal per frequency. Ultimately, combining these maps lead to the best 2018 HFI measurement of the [[#HFI 2018 Solar dipole | '''Solar dipole parameters''']]. | ||
| + | |||
| + | Note that this is an iterative process. Ultimately, CMB analysis should combine all these steps within the same mapmaking process. | ||
== Calibration accuracy == | == Calibration accuracy == | ||
| − | The dipole calibration accuracy . | + | The orbital dipole calibration accuracy on frequency bands can be tested using the Solar dipole. |
| − | |||
| − | |||
| − | + | 1. End-to-end simulations give a tool to test the biais and uncertainties induced by the Sroll processing, by comparing the Solar dipole amplitude input and output. The following numbers are extracted from Table 7 of {{PlanckPapers|planck2016-l03}}, and give, for each frequency band, this absolute frequency bias, based on 100 end-to-end simulations: | |
| − | + | *at 100 GHz: 8.0 x 10<sup>-5</sup> ± 1.5 x 10<sup>-4</sup> | |
| + | *at 143 GHz: 2.1 x 10<sup>-4</sup> ± 1.1 x 10<sup>-4</sup> | ||
| + | *at 217 GHz: 2.8 x 10<sup>-4</sup> ± 1.4 x 10<sup>-4</sup> | ||
| + | *at 353 GHz: 2.4 x 10<sup>-4</sup> ± 3.9 x 10<sup>-4</sup> | ||
| − | + | 2. The Solar dipole is obtained by removing from the primary frequency maps, the CMB anisotropies (obtained by 4 different component separation methods), and the foreground maps (dominated by dust). Uncertainties on this determination are due to residual dipoles from the CMB anisotropies removal, and from the dust removal, which are tested by the dispersion in component separation methods and along different sky fractions. The best Solar dipole determination is obtained by combining the 100, 143 and 217 GHz data. | |
| − | + | We construct an estimate of uncertainty on the Solar dipole amplitude starting from the statistical uncertainties given, for a given sky fraction and CMB extraction, by the ''SRoll'' algorithm (0.09 μK rms), referred to as "stat". Nevertheless the dispersion observed with sky fraction and the four component separation methods is a factor an order of magnitude larger (0.91 μK). This includes both the effect of the dust residuals (traced by sky fraction) and CMB dipole removal residual (traced by the four component separation methods). Furthermore, the absolute \sroll\ bias measured on the Solar dipole is (0.64 ± 0.46)μK, referred to as "cal'" | |
| − | + | We thus obtain the best [[#HFI 2018 Solar dipole|'''HFI 2018 Solar dipole''']] determination which gives the uncertainty on the photometric calibration. | |
| − | | | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Transfer function effects lead to an inter-calibration accuracy of the 3 CMB channels better than $1\time10^{-3}$ at the first acoustic peak, rising to $3\time10^{-3}$ at the third peak. | |
| − | ==== | + | ==== HFI 2018 Solar dipole ==== |
| − | |||
| − | + | From the steps described above and detailled in {{PlanckPapers|planck2016-l03}}, we obtain the best HFI 2018 Solar dipole velocity vector and amplitude (which is directly obtained from the Earth orbital dipole). Note that the accuracy of the measurement depends on all steps described. We also give the amplitude in temperature, based on the CMB temperature as used in the 2015 release: | |
| − | |||
| − | + | '''v = (369.8150 ± 0.0010) km s<sup>-1</sup>''' | |
| − | |||
| − | + | '''A = (3362.08 ± 0.09 (stat.) ± 0.45 (syst.) ± 0.32 (cal.) μK''' | |
| − | |||
| + | '''l = (264.021 ± 0.003 (stat.) ± 0.0079 (syst.) )°''' | ||
| − | + | '''b = (48.253 ± 0.001 (stat.) ± 0.0037 (syst.) )°''' | |
| − | |||
| − | + | == Overall quality assessment == | |
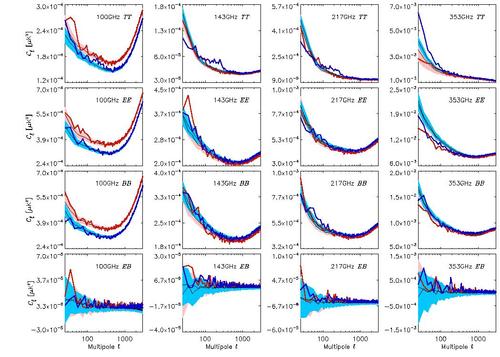
| − | + | Several null tests have been used (detset, hm, odd-even rings). The power spectra of the associated map differences are well reproduced by the end-to-end simulations, including all significant systematic effects. This shows that, at this level of accuracy, there is no unidentified systematics. | |
| − | + | [[File:newpte.pdf|thumb|center|500px|'''Figure 17 of ({{PlanckPapers|planck2016-l03}}. ''']] | |
| − | |||
| − | |||
| − | == Complementary figures of the HFI | + | == Complementary figures of the HFI DPC paper == |
| − | Complementary figures of the HFI 2018 DPC paper ( {{PlanckPapers|planck2016-l03}}) are given [[Appendix_of_HFI_DPC_paper| HERE]]. | + | Complementary figures of the HFI 2018 DPC paper ({{PlanckPapers|planck2016-l03}}) are given [[Appendix_of_HFI_DPC_paper| HERE]]. |
== Previous Releases: (2015) and (2013) Mapmaking and photometric calibration == | == Previous Releases: (2015) and (2013) Mapmaking and photometric calibration == | ||
Latest revision as of 07:44, 18 January 2019
Contents
[hide]Introduction[edit]
This section gives an overview of the mapmaking and the calibration procedures used to build the HFI maps.
- Procedures for the 2013 release is to be found in Planck-2013-VI[1] and Planck-2013-VIII[2] (see at the bottom of this page)
- Procedures for the 2015 release is to be found in Planck-2015-A08[3] (see at the bottom of this page)
- In 2016, a new procedure called SRoll has been introduced to extract, from the sky, parameters for systematics important to the mapmapking. This is achieved through a generalized polarized destriper which uses the redundancy between detectors inside a frequency band. Systematic effects producing leakages from intensity to polarization contribute strongly to this determinations. This allowed for the first time the use of large scale polarized data and the extraction of the reionization parameter. The procedure and its results are described in Planck-2016-XLVI[4].
- For the 2018 legacy release, the same SRoll procedure has been used to produce the frequency intensity and polarization maps. Planck-2020-A3[5] fully describes the procedures, the products and their characterization.
SRoll global solution[edit]
Inputs to SRoll[edit]
For the 2018 release, the TOI processing remains unchanged from the previous 2015 release (see TOI processing). As mentionned, a small cut of in the data selection (1000 pointing periods) has been done at the end of the cryogenic mission.
SRoll scheme[edit]
SRoll makes use of an extended destriper. Destriper methods have been used previously to remove baseline drifts from detector time streams, while making co-added maps of the data, by taking advantage of the redundancy in the scanning strategy. SRoll is a generalized polarized destriper which, in addition, compares all the observations of the same sky pixel by the same detector with different polarization angles, as well as by different detectors within the same frequency band. It thus fits differences between instrument parameters that minimize the difference between all polarized observations of the same sky pixel in the same frequency band. It solves consistently for:
- one offset for each pointing period,
- an empirical transfer function adding to the correction already done in the TOI processing (time constants less than 3 seconds), covering time constants up to 30 seconds,
- a CMB calibration mismatch between detectors, detected through the shift on the total kinetic dipole, between odd and even surveys, inducing leakage from intensity to polarization,
- a bandpass mismatch for foregrounds response due to color corrections with respect to the CMB calibration, also inducing leakage from intensity to polarization. This makes use of an input spatial template (2015 Planck component separation results) of each foreground,
- the absolute calibration from the orbital dipole (the kinetic dipole associated with the Earth motion around the Sun) which does not project on the sky.
The destripper is only sensitive to differences between bolometer coefficients. Thus, the absolute average value of the parameters within a frequency band is taken imposing:
- the sum of the offsets to be zero (no monopoles),
- the average of the additional color corrections (for both dust and free-free emission) to be zero, thus keeping the same average as the ground-based one.
.
SRoll outputs[edit]
1. SRoll ouputs are frequency sky maps (hereafater called "primary frequency maps"). These include the Solar dipole signal (i.e. the kinetic dipole associated with the motion of the Solar system with respect to the CMB) which projects on the sky. Combining these primary maps allows to separate the different components, and extract the Solar dipole.
2. From these primary frequency maps, the Planck 2015 Solar dipole (d,l,b)= (3364.5 ± 2.0 μK, 264.00 ± 0.03°, 48.24 ± 0.02°) is then removed leading to the delivered PR3 HFI frequency maps.
3. The HFI frequency maps, combined with the LFI ones, lead, thanks to component separation methods, to physical component maps: CMB maps and diffuse foregrounds maps.
4. Removing the CMB anisotropies and diffuse foreground component maps from the primary frequency maps leaves a Solar dipole signal per frequency. Ultimately, combining these maps lead to the best 2018 HFI measurement of the Solar dipole parameters.
Note that this is an iterative process. Ultimately, CMB analysis should combine all these steps within the same mapmaking process.
Calibration accuracy[edit]
The orbital dipole calibration accuracy on frequency bands can be tested using the Solar dipole.
1. End-to-end simulations give a tool to test the biais and uncertainties induced by the Sroll processing, by comparing the Solar dipole amplitude input and output. The following numbers are extracted from Table 7 of Planck-2020-A3[5], and give, for each frequency band, this absolute frequency bias, based on 100 end-to-end simulations:
- at 100 GHz: 8.0 x 10-5 ± 1.5 x 10-4
- at 143 GHz: 2.1 x 10-4 ± 1.1 x 10-4
- at 217 GHz: 2.8 x 10-4 ± 1.4 x 10-4
- at 353 GHz: 2.4 x 10-4 ± 3.9 x 10-4
2. The Solar dipole is obtained by removing from the primary frequency maps, the CMB anisotropies (obtained by 4 different component separation methods), and the foreground maps (dominated by dust). Uncertainties on this determination are due to residual dipoles from the CMB anisotropies removal, and from the dust removal, which are tested by the dispersion in component separation methods and along different sky fractions. The best Solar dipole determination is obtained by combining the 100, 143 and 217 GHz data.
We construct an estimate of uncertainty on the Solar dipole amplitude starting from the statistical uncertainties given, for a given sky fraction and CMB extraction, by the SRoll algorithm (0.09 μK rms), referred to as "stat". Nevertheless the dispersion observed with sky fraction and the four component separation methods is a factor an order of magnitude larger (0.91 μK). This includes both the effect of the dust residuals (traced by sky fraction) and CMB dipole removal residual (traced by the four component separation methods). Furthermore, the absolute \sroll\ bias measured on the Solar dipole is (0.64 ± 0.46)μK, referred to as "cal'"
We thus obtain the best HFI 2018 Solar dipole determination which gives the uncertainty on the photometric calibration.
Transfer function effects lead to an inter-calibration accuracy of the 3 CMB channels better than $1\time10^{-3}$ at the first acoustic peak, rising to $3\time10^{-3}$ at the third peak.
HFI 2018 Solar dipole[edit]
From the steps described above and detailled in Planck-2020-A3[5], we obtain the best HFI 2018 Solar dipole velocity vector and amplitude (which is directly obtained from the Earth orbital dipole). Note that the accuracy of the measurement depends on all steps described. We also give the amplitude in temperature, based on the CMB temperature as used in the 2015 release:
v = (369.8150 ± 0.0010) km s-1
A = (3362.08 ± 0.09 (stat.) ± 0.45 (syst.) ± 0.32 (cal.) μK
l = (264.021 ± 0.003 (stat.) ± 0.0079 (syst.) )°
b = (48.253 ± 0.001 (stat.) ± 0.0037 (syst.) )°
Overall quality assessment[edit]
Several null tests have been used (detset, hm, odd-even rings). The power spectra of the associated map differences are well reproduced by the end-to-end simulations, including all significant systematic effects. This shows that, at this level of accuracy, there is no unidentified systematics.
Complementary figures of the HFI DPC paper[edit]
Complementary figures of the HFI 2018 DPC paper (Planck-2020-A3[5]) are given HERE.
Previous Releases: (2015) and (2013) Mapmaking and photometric calibration[edit]
2015 Mapmaking and photometric calibration
2013 Mapmaking and photometric calibration
References[edit]
- ↑ Jump up to: 1.01.11.21.31.41.5 Planck 2013 results. VI. High Frequency Instrument Data Processing, Planck Collaboration, 2014, A&A, 571, A6.
- ↑ Jump up to: 2.02.12.2 Planck 2013 results. VIII. HFI photometric calibration and Map-making, Planck Collaboration, 2014, A&A, 571, A8.
- ↑ Jump up to: 3.03.13.23.33.43.5 Planck 2015 results. VIII. High Frequency Instrument data processing: Calibration and maps, Planck Collaboration, 2016, A&A, 594, A8.
- Jump up ↑ Planck intermediate results. XLVI. Reduction of large-scale systematic effects in HFI polarization maps and estimation of the reionization optical depth, Planck Collaboration Int. XLVI A&A, 596, A107, (2016).
- ↑ Jump up to: 5.05.15.25.35.4 Planck 2018 results. III. High Frequency Instrument data processing and frequency maps, Planck Collaboration, 2020, A&A, 641, A3.
- ↑ Jump up to: 6.06.1 Planck 2013 results. XIII. Galactic CO emission, Planck Collaboration, 2014, A&A, 571, A13.
- ↑ Jump up to: 7.07.17.2 Planck 2015 results. X. Diffuse component separation: Foreground maps, Planck Collaboration, 2016, A&A, 594, A10.
- Jump up ↑ Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
- Jump up ↑ Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results, G. Hinshaw, J. L. Weiland, R. S. Hill, N. Odegard, D. Larson, C. L. Bennett, J. Dunkley, B. Gold, M. R. Greason, N. Jarosik, E. Komatsu, M. R. Nolta, L. Page, D. N. Spergel, E. Wollack, M. Halpern, A. Kogut, M. Limon, S. S. Meyer, G. S. Tucker, E. L. Wright, ApJS, 180, 225-245, (2009).
- Jump up ↑ Planck 2013 results. XV. CMB power spectra and likelihood, Planck Collaboration, 2014, A&A, 571, A15.
- Jump up ↑ Planck 2013 results. XXXI. Consistency of Planck data, Planck Collaboration, 2014, A&A, 571, A31.
(Planck) High Frequency Instrument
Cosmic Microwave background
(Planck) Low Frequency Instrument
Data Processing Center
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
analog to digital converter
Noise Equivalent Power
Full-Width-at-Half-Maximum
reduced IMO
Planck Sky Model