Simulation data
Contents
Introduction[edit]
The 2015 Planck data release is supported by a set of simulated maps of the sky, by astrophysical component, and of that sky as seen by Planck (fiducial mission realizations), together with separate sets of Monte Carlo realizations of the CMB and the instrument noise. They contain the dominant instrumental (detector beam, bandpass, and correlated noise properties), scanning (pointing and flags), and analysis (map-making algorithm and implementation) effects. These simulations have been described in Planck-2015-A12[1].
In addition to the baseline maps made from the data from all detectors at a given frequency for the entire mission, there are a number of data cuts that are mapped both for systematics tests and to support cross-spectral analyses. These include
- detector subsets (“detsets”), comprising the individual unpolarized detectors and the polarized detector quadruplets corresponding to each leading trailing horn pair. Note that HFI sometimes refers to full channels as detset0; here detset only refers to subsets of detectors.
- mission subsets, comprising the surveys, years, and half-missions, with exact boundary definitions given in Planck-2015-A02[2] and Planck-2015-A07[3] for LFI and HFI, respectively.
- half-ring subsets, comprising the data from either the first or the second half of each pointing-period ring
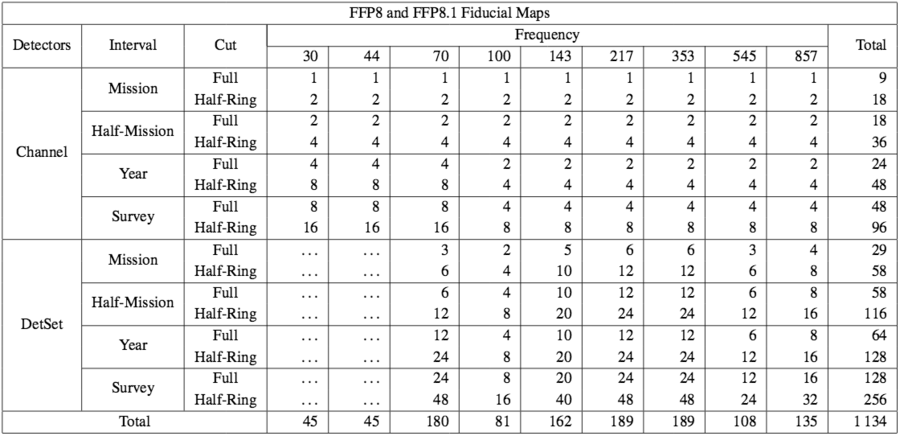
The various combinations of these data cuts then define 1134 maps, as enumerated in the top section of Table 1 from Planck-2015-A12[1]. The different types of map are then named according to their included detectors (channel or detset), interval (mission, half-mission, year or survey), and ring-content (full or half-ring); for example the baseline maps are described as channel/mission/full, etc.
The simulation process consists of
- modeling each astrophysical component of the sky emission for each Planck detector, using Planck data and the relevant characteristics of the Planck instruments.
- simulating each detector's observation of each sky component following the Planck scanning strategy and using the best estimates of the detector's beam and noise properties (obtained in flight), then combining these timelines into a single one per detector, and projecting these simulated timelines onto observed maps (the fiducial sky), as is done with the on-orbit data;
- generating Monte Carlo realizations of the CMB and of the noise, again following the Planck scanning strategy and using our best estimates of the detector beams and noise properties respectively.
The first step is performed by the Planck Sky Model (PSM), and the last two by the Planck Simulation Tools (PST), both of which are described in the sections below.
The production of a full focal plane (FFP) simulation, and including the many MC realizations of the CMB and the noise, requires both HFI and LFI data and includes large, computationally challenging, MC realizations. They are too large to be generated on either of the DPC's own cluster. Instead the PST consists of three distinct tools, each designed to run on the largest available supercomputers, that are used to generate the fiducial sky realization, the CMB MC, and the noise MC respectively. The simulations delivered here are part of the 8th generation FFP simulations, known as FFP8. They were primarily generated on the National Energy Research Scientific Computing Center (NERSC) in the USA and at CSC–IT Center for Science (CSC) in Finland.
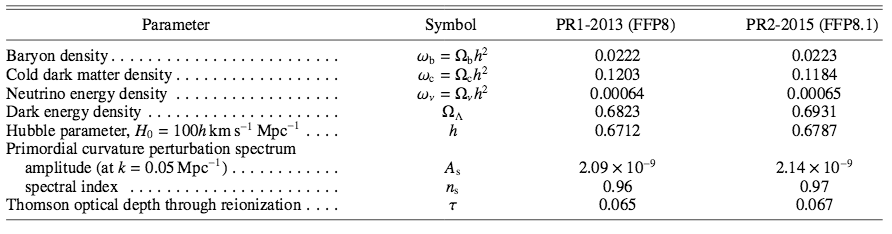
The fiducial realizations include instrument noise, astrophysical foregrounds, and the lensed scalar, tensor, and non-Gaussian CMB components, and are primarily designed to support the validation and verification of analysis codes. To test our ability to detect tensor modes and non-Gaussianity, we generate five CMB realizations with various cosmologically interesting -- but undeclared -- values of the tensor-to-scalar ratio r and non-Gaussianity parameter fNL. To investigate the impact of differences in the bandpasses of the detectors at any given frequency, the foreground sky is simulated using both the individual detector bandpasses and a common average bandpass, to include and exclude the effects of bandpass mismatch. To check that the PR2-2015 results are not sensitive to the exact cosmological parameters used in FFP8 we subsequently generated FFP8.1, exactly matching the PR2-2015 cosmology.
Since mapmaking is a linear operation, the easiest way to generate all of these different realizations is to build the full set of maps of each of six components:
- the lensed scalar CMB (cmb_scl});
- the tensor CMB (cmb_ten);
- the non-Gaussian complement CMB (cmb_ngc);
- the forgreounds including bandpass mismatch (fg_bpm);
- the foregrounds excluding bandpass mismatch (fg_nobpm);
- the noise (noise).
We then sum these, weighting the tensor and non-Gaussian complement maps with and fNL, respectively, and including one of the two foreground maps, to produce 10 total maps of each type. The complete fiducial data set then comprises 18,144 maps.
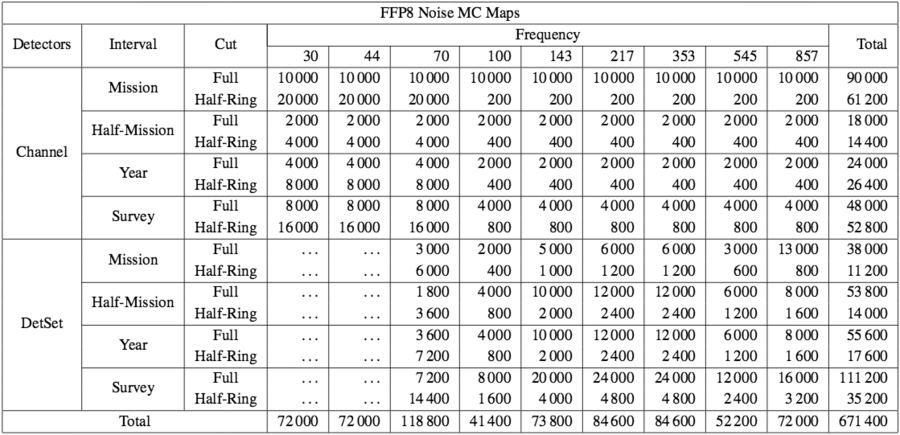
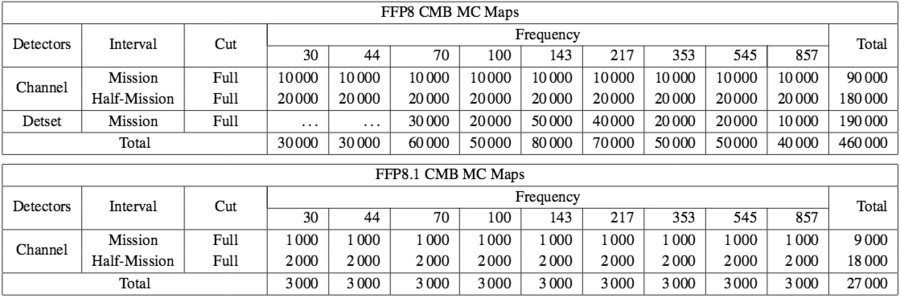
While the full set of maps can be generated for the fiducial cases, for the 104-realization MC sets this would result in some 107 maps and require about 6 PB of storage. Instead, therefore, the number of realizations generated for each type of map is chosen to balance the improved statistics it supports against the computational cost of its generation and storage. The remaining noise MCs sample broadly across all data cuts, while the additional CMB MCs are focused on the channel/half-mission/full maps and the subset of the detset/mission/full maps required by the "commander" component separation code Planck-2015-A10[4].
The goal of FFP8 is to simulate the Planck mission as accurately as possible; however, there are a number of known systematic effects that are not included, either because they are removed in the pre-processing of the time-ordered data (TOD), or because they are insufficiently well-characterized to simulate reliably, or because their inclusion (simulation and removal) would be too computationally expensive. These systematic effects are discussed in detail in Planck-2015-A02[2] and Planck-2015-A07[3] and include:
- cosmic ray glitches (HFI);
- spurious spectral lines from the 4-K cooler electronics (HFI);
- nonlinearity in the analogue-to-digital converter (HFI);
- imperfect reconstruction of the focal plane geometry.
Note that if the residuals from the treatment of any of these effects could be mapped in isolation, then maps of such systematics could simply be added to the existing FFP8 maps to improve their correspondence to the real data.
Mission and instrument characteristics[edit]
The goal of FFP8 is to simulate the Planck mission as accurately as possible; however, there are a number of known systematic effects that are not included, either because they are removed in the pre-processing of the time-ordered data (TOD), or because they are insufficiently well-characterized to simulate reliably, or because their inclusion (simulation and removal) would be too computationally expensive. These systematic effects are discussed in detail in Planck-2015-A02[2] and Planck-2015-A07[3] and include:
- cosmic ray glitches (HFI);
- spurious spectral lines from the 4-K cooler electronics (HFI);
- nonlinearity in the analogue-to-digital converter (HFI);
- imperfect reconstruction of the focal plane geometry.
Note that if the residuals from the treatment of any of these effects could be mapped in isolation, then maps of such systematics could simply be added to the existing FFP8 maps to improve their correspondence to the real data.
Pointing[edit]
The FFP8 detector pointing is calculated by interpolating the satellite attitude to the detector sample times and by applying a fixed rotation from the satellite frame into the detector frame. The fixed rotations are determined by the measured focal plane geometry as shown in Planck-2015-A04[5] and Planck-2015-A07[3], while the satellite attitude is described in the Planck attitude history files (AHF). The FFP pointing expansion reproduces the DPC pointing to sub-arcsecond accuracy, except for three short and isolated instances during Surveys 6--8 where the LFI sampling frequency was out of specification. Pixelization of the information causes the pointing error to be quantized to either zero (majority of cases) or the distance between pixel centres ( and for LFI and HFI, respectively). Since we need a single reconstruction that will serve both instruments efficiently in a massively parallel environment, we use the pointing provided by the Time Ordered Astrophysics Scalable Tools (Toast) package.
Noise[edit]
We require simulated noise realizations that are representative of the noise in the flight data, including variations in the noise power spectral density (PSD) of each detector over time. To obtain these we developed a noise estimation pipeline complementary to those of the DPCs. The goal of DPC noise estimation is to monitor instrument health and to derive optimal noise weighting, whereas our estimation is optimized to feed into noise simulation. Key features are the use of full mission maps for signal subtraction, long (about 24 hour) realization length, and the use of autocorrelation functions in place of Fourier transforms to handle flagged and masked data (HFI).
Beams[edit]
The simulations use the so-called scanning beams (e.g., Planck-2013-VI[6]), which give the point-spread function of for a given detector including all temporal data processing effects: sample integration, demodulation, ADC nonlinearity residuals, bolometric time constant residuals, etc. In the absence of significant residuals (LFI), the scanning beams may be estimated from the optical beams by smearing them in the scanning direction to match the finite integration time for each instrument sample. Where there are unknown residuals in the timelines (HFI), the scanning beam must be measured directly from observations of strong point-like sources, namely planets. If the residuals are present but understood, it is possible to simulate the beam measurement and predict the scanning beam shape starting from the optical beam.
For FFP8, the scanning beams are expanded in terms of their spherical harmonic coefficients, , with the order of the expansion (maximum and m considered) representing a trade-off between the accuracy of the representation and the computational cost of its convolution. The LFI horns have larger beams with larger sidelobes (due to their location on the outside of the focal plane), and we treat them as full beams divided into main (up to , , and for 30, 44, and 70 GHz, respectively), intermediate (up to 5), and sidelobe (above 5) components Planck-2015-A04[5]. This division allows us to tune the expansion orders of the three components separately. HFI horns are limited to the main beam component, measured out to 100 arc minutes Planck-2015-A07[3]. Since detector beams are characterized independently, the simulations naturally include differential beam and pointing systematics.
Bandpasses[edit]
Both the LFI and HFI detector bandpasses are based on ground measurements (see Planck-2013-IX[7], respectively), although flight data processing for LFI now uses in-flight top-hat approximations rather than the ground measurements that were found to contain systematic errors. Differences in the bandpasses of detectors nominally at the same frequency (the so-called bandpass mismatch) generate spurious signals in the maps, since each detector is seeing a slightly different sky while the mapmaking algorithms assume that the signal in a pixel is the same for all detectors. To quantify the effect of these residuals, in FFP8 we generate detector timelines from foreground maps in two ways, one that incorporates the individual detector bandpasses, the other using an average bandpass for all the detectors at a given frequency.
This effect of the bandpass mismatch can be roughly measured from either flight or simulated data using so-called spurious component mapmaking, which provides noisy all-sky estimates of the observed sky differences (the spurious maps), excluding polarization, between individual detectors and the frequency average. We compare the amount of simulated bandpass mismatch to flight data. The spurious component approach is detailed in the Appendix of Planck-2015-A12[1]. Mismatch between FFP8 and flight data is driven by inaccurate bandpass description (LFI) and incomplete line emission simulation (HFI). The noisy pixels that align with the Planck scanning rings in the HFI maps are regions where the spurious map solution is degenerate with polarization due to insufficient observation orientations.
The Planck Sky Model[edit]
Overall description[edit]
The Planck Sky Model, PSM, consists of a set of data and of code used to simulate sky emission at millimeter-wave frequencies; it is described in detail in Delabrouille et al., (2013)[8], henceforth the PSM paper..
The Planck Sky Model is available here: http://www.apc.univ-paris7.fr/~delabrou/PSM/psm.html
The main simulations used to test and validate the Planck data analysis pipelines (and, in particular, component separation) makes use of simulations generated with version 1.9 of the PSM software. The total sky emission is built from the CMB plus ten foreground components, namely thermal dust, spinning dust, synchrotron, CO lines, free-free, thermal Sunyaev-Zel'dovich (SZ) effect (with first order relativistic corrections), kinetic SZ effect, radio and infrared sources, Cosmic Infrared Background (CIB).
The CMB is modeled using CAMB. It is based on adiabatic initial perturbations, with the following cosmological parameters:
The Galactic ISM emission comprises five components: thermal dust, spinning dust, synchrotron, free-free, CO lines (the J=1->0, J=2->1, and J=3->2 lines at 115.27, 230.54, and 345.80 GHz, respectively), and plus the cosmic infrared background (CIB), emission from radio sources, and the thermal and kinetic Sunyaev-Zeldovich (SZ) effects.
The thermal dust emission is modelled using single-frequency template maps of the intensity and polarization, together with a pixel-dependent emission law. For FFP8 the thermal dust emission templates are derived from the Planck 353 GHz observations. This update of the original PSM dust model is necessary to provide a better match to the emission observed by Planck. While one option would be simply to use the dust opacity map obtained in Planck-2013-XI[9], this map still suffers from significant contamination by CIB anisotropies and infrared point sources. Using it as a 353 GHz dust template in simulations would result in an excess of small scale power (from CIB and infrared sources) scaling exactly as thermal dust across frequencies. The resulting component represents correctly neither dust alone (because of an excess of small scale power) nor the sum of dust and infrared sources (because the frequency scaling of the CIB and infrared sources is wrong). For simulation purposes, the main objective is not to have an exact map of the dust, but instead a map that has the right statistical properties. Hence we produce a template dust map at 353 GHz by removing that fraction of the small-scale power that is due to CIB emission, infra-red sources, CMB, and noise.
The spinning-dust map used for FFP8 simulations is a simple realization of the spinning dust model, post-processed to remove negative values occurring in a few pixels because of the generation of small-scale fluctuations on top of the spinning dust template extracted from WMAP data.
The FFP8 synchrotron emission is modelled on the basis of the template emission map observed at 408 MHz by Haslam et al. (1982). This template synchrotron map is extrapolated in frequency using a spectral index map corresponding to a simple power law.
The free-free spectral dependence is modelled in FFP8 by assuming a constant electron temperature T_{e} = 7000 K. Electron-ion interactions in the ionized phase of the ISM produce emission that is in general fainter than both the synchrotron and the thermal dust emission outside of the active star-forming regions in the Galactic plane. The free-free model uses a single template, which is scaled in frequency by a specific emission law. The free-free spectral index is a slowly varying function of frequency and depends only slightly on the local value of the electron temperature.
The radio sources are modelled in FFP8 in a different way from the pre-launch versions of the PSM.
For strong radio sources (S_{30} > 0.5 Jy), we use radio sources at 0.84, 1.4, or 4.85 GHz. For sources observed at two of these frequencies, we extrapolate or interpolate to the third frequency assuming the spectral index estimated from two observed. For sources observed at only one frequency, we use differential source counts to obtain the ratio of steep- to flat-spectrum sources in each interval of flux density considered. From this ratio, we assign spectral indices (randomly) to each source within each flux density interval. Fiducial Gaussian spectral index distributions as a function of spectral class are obtained from the literature. These are then adjusted slightly until there is reasonable agreement between the PSM differential counts and the predicted model counts predicted.
For faint radio sources (S_{30} <= 0.5 Jy), the pre-launch PSM showed a deficit of sources resulting from inhomogeneities in surveys at different depths. We address this issue by constructing a simulated catalogue of sources at 1.4\,GHz. We replace the simulated sources by the observed ones, wherever possible. If, however, in any particular pixel, we have a shortfall of observed sources, we make up the deficit with the simulated sources. Every source in this new catalogue is given a model-derived spectral class. We thus assign a spectral index to each source based on the spectral class, and model the spectrum of each source using four power laws. We also assume some steepening of the spectral index with frequency, with fiducial values of the steepening obtained from the literature.
We combine the faint and strong radio source catalogues we constructed and compute the differential source counts on these sources between 0.005 Jy and 1 Jy. Finally we also model the polarization of these radio sources using the measured polarization fractions from the literature; for each simulated source we draw a polarization fraction at random from the list of real sources of the same spectral type.
The SZ clusters are simulated following the model of Delabrouille, Melin, and Bartlett (DMB) as implemented in the PSM. A catalogue of halos is drawn from a Poisson distribution of the mass function with a limiting mass of M500,true > 2x1013. We use the pressure profile from the literature to model the thermal SZ emission of each halo given its redshift and mass. We determine the cluster temperature and assume that the profiles are isothermal. These steps allow us to compute the first-order thermal relativistic correction and the kinetic SZ effect for each cluster, both of which are included in the simulation. Finally, we inject catalogued clusters following the same model, and remove from the simulation corresponding clusters in each redshift and mass range. Hence the SZ simulation features the majority of known X-ray and optical clusters, and is fully consistent with X-ray scaling laws and observed \Planck\ SZ counts.
The CIB model used to simulate FFP8 relies on the distribution of individual galaxies in template maps based on the distribution of dark matter at a range of relevant redshifts. We assume the CIB galaxies can be grouped into three different populations (proto-spheroid, spiral, starburst). Within each population, galaxies have the same SED, while the flux density is randomly distributed according to redshift-dependent number counts obtained from JCMT/SCUBA-2 observations and the Planck ERCSC, as well as observations from Herschel-SPIRE and AzTEC/ASTE. We use the Class software to generate dark matter maps at 17 different redshifts between 1 and 5.5. Since the galaxy distribution does not exactly follow the dark matter distribution, we modify the alm coefficients of dark matter anisotropies given by Class. Template maps generated from the alm coefficients are then exponentiated to avoid negative pixels. Galaxies are randomly distributed with a probability of presence proportional to the pixel values of the template maps. One map is generated for each population, at each redshift, and associated with a redshifted SED depending on the population. The emission of these maps (initially at a reference frequency) can be extrapolated to any frequency using the associated redshifted SED. By summing the emission of all maps, we can generate CIB maps at any frequency in the range of validity of our model.
See Planck-2015-A12[1] and references therein for a very detailed explanation of the procedures to simulate each of the components.
PSM Products[edit]
The sky model is simulated at a resolution common to all components by smoothing the maps with an ideal Gaussian beam of FWHM of 4 arcminute. The \healpix\footnote{\url{http://healpix.sourceforge.net}} pixelization in Galactic coordinates is used for all components, with Nside = 2048 and = 6000. Sky emission maps are generated by numerically band-integrating the sky model maps (emission law of each component, in each pixel) over the frequency bands both of each detector in the focal plane and -- using an average over the detectors at a given frequency -- of each channel. The band-integrated maps are essentially observations of the model sky simulated by an ideal noiseless instrument with ideal Gaussian beams of FWHM equal to the resolution of the model sky.
PSM maps of the fiducial sky are given in the following map products:
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-030_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-044_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-070_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-100_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-143_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-217_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-353_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-545_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-857_2048_R2.00_full.fits
and bandpass mismatch corrected (nobpm)
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-030_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-044_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-070_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-100_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-143_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-217_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-353_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-545_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-857_2048_R2.00_full.fits
Each file contains a BINTABLE extension with three maps: I, Q and U between 30 and 353 GHz and I for the others. The Units are KCMB between 30 and 353 GHz, and MJy/sr for the others.
Note: Original PSM foreground components has been generated at NSIDE 2048 and using a gaussian beam of 4 arcmin. LFI CMB maps has been downgraded at NSIDE 1024.
The Fiducial Sky Simulations[edit]
For each detector, fiducial time-ordered data are generated separately for each of the ten PSM components using the LevelS software[10] as follows:
- the detector's beam and PSM map are converted to spherical harmonics using beam2alm and anafast respectively;
- the beam-convolved map value is calculated over a 3-dimensional grid of sky locations and beam orientations using conviqt;
- the map-based timelines are calculated sample-by-sample by interpolating over this grid using multimod;
- the catalogue-based timelines are produced sample-by-sample by beam-convolving any point source laying within a given angular distance of the pointing at each sample time using multimod.
For each frequency, fiducial sky maps are generated for
- the total signal (i.e. sky + instrument noise), for both the nominal mission and the halfrings thereof (see details)
- the foreground sky alone (excluding CMB but including noise),
- the point source sky, and
- the noise alone
All maps are built using the MADAM destriping map-maker[11] interfaced with the TOAST data abstraction layer . In order to construct the total timelines required by each map, for each detector TOAST reads the various component timelines separately and sums then, and, where necessary, simulates and adds a noise realization time-stream on the fly. HFI frequencies are mapped at HEALPix resolution Nside=2048 using ring-length destriping baselines, while LFI frequencies are mapped at Nside=1024 using 1s baselines.
Products delivered[edit]
A single simulation is delivered, which is divided into two types of products:
1. six files of the full sky signal at each HFI and LFI frequency, and their corresponding halfring maps:
- These files have the same structure as the equivalent SkyMap products described in the Frequency Maps chapter, namely one BINTABLE extension with three columns containing 1) Signal, 2) hit-count, and 3) variance. Units are KCMB for all channels.
2. Three files containing 1) the sum of all astrophysical foregrounds, 2) the point sources alone, and 3) the noise alone: which are subproducts of the above, and are in the form of the PSM maps described in the previous section.
- HFI_SimMap_foreground_2048_R1.10_nominal.fits
- HFI_SimMap_noise_2048_R1.10_nominal.fits
- HFI_SimMap_ps_2048_R1.10_nominal.fits
- LFI_SimMap_foreground_1024_R1.10_nominal.fits
- LFI_SimMap_noise_1024_R1.10_nominal.fits
- LFI_SimMap_ps_1024_R1.10_nominal.fits
These files have the same structure as the PSM output maps described above, namely a single BINTABLE extension with 6 columns named F100 -- F857 each containing the given map for that HFI band and with 3 columns named F030, F044, F070 each containing the given map for that LFI band. Units are alway KCMB.
Note that the CMB alone is not delivered as a separate product, but it can be recovered by simple subtraction of the component maps for the total signal map.
Monte Carlo realizations of CMB and of noise[edit]
The CMB MC set is generated using FEBeCoP[12], which generates an effective beam for each pixel in a map at each frequency by accumulating the weights of all pixels within a fixed distance of that pixel, summed over all observations by all detectors at that frequency. It then applies this effective beam pixel-by-pixel to each of 1000 input CMB sky realizations.
The noise MC set is generated just as the fiducial noise maps, using MADAM/TOAST. In order to avoid spurious correlations within and between the 1000 realizations, each stationary interval for each detector for each realization is generated from a distinct sub-sequence of a single statistically robust, extremely long period, pseudo-random number sequence.
Products delivered[edit]
100 realizations of the CMB (lensed) and of the noise are made available. They are named
- HFI_SimMap_cmb-{nnnn}_2048_R1.nn_nominal.fits
- HFI_SimMap_noise-{nnnn}_2048_R1.nn_nominal.fits
- LFI_SimMap_cmb-{nnnn}_2048_R1.nn_nominal.fits
- LFI_SimMap_noise-{nnnn}_2048_R1.nn_nominal.fits
where nnnn ranges from 0000 to 0099.
The FITS file structure is the same as for the other similar products above, with a single BINTABLE extension with six columns, one for each HFI frequency, named F100, F143, … , F857 and with three columns, one for each LFI frequency, named F030, F044, F070. Units are always microKCMB(NB: due to an error in the HFI file construction, the unit keywords in the headers indicate KCMB, the "micro" is missing there).
Products delivered in PLA[edit]
In the Planck Legacy Archive, the 2015 simulations are delivered as follows :
- 1000 Monte-Carlo realizations from the ffp8 series (noise and CMB scalar) - full maps only
- the 1001 Monte-Carlo realizations from the ffp9 series (CMB scalar only) - full maps only
- the ffp8 fiducial sky for band-pass mismatch and no band-pass mismatch
The files can be found in the PLA in Maps - Advanced search - Simulated maps search.
All the rest of the ffp8 and ffp9 simulations can be found on NERSC at /project/projectdirs/planck/data/
Lensing Simulations[edit]
The lensing simulations package contains 100 realisations of the Planck 2014 "MV" lensing potential estimate, as well as the input lensing realizations. They can be used to determine error bars as well eas effective normalizations for cross-correlation with other tracers of lensing. These simulations are of the lensing convergence map contained in the Lensing map release file. The production and characterisation of this lensing potential map are described in detail in [13], which also describes the procedure used to generate the realizations given here.
The simulations are delivered as a gzipped tarball of approximately 8 GB in size. For delivery purposes, the package has been split into 2GB chunks using the unix command
- split -d -b 2048m
After downloading the individual chunks, the full tarball can be reconstructed with the command
- cat COM_SimMap_Lensing_R0.00.tar.* | tar xvf -
The contents of the tarball are described below:
| Filename | Format | Description |
|---|---|---|
| obs_klms/sim_????_klm.fits | HEALPIX FITS format alm, with | Contains the simulated convergence estimate for each simulation. |
| sky_klms/sim_????_klm.fits | HEALPIX FITS format alm, with | Contains the input lensing convergence for each simulation. |
| inputs/mask.fits.gz | HEALPIX FITS format map, with | Contains the lens reconstruction analysis mask. |
| inputs/cls/cl??.dat | ASCII text file, with columns = (, ) | Contains the fiducial theory CMB power spectra for TT, EE, BB, and , with temperature and polarization in units of . |
References[edit]
- ↑ 1.01.11.21.3 Planck 2015 results. XII. Full Focal Plane Simulations, Planck Collaboration, 2016, A&A, 594, A12.
- ↑ 2.02.12.2 Planck 2015 results. II. LFI processing, Planck Collaboration, 2016, A&A, 594, A2.
- ↑ 3.03.13.23.33.4 Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
- ↑ Planck 2015 results. X. Diffuse component separation: Foreground maps, Planck Collaboration, 2016, A&A, 594, A10.
- ↑ 5.05.1 Planck 2015 results. IV. LFI beams and window functions, Planck Collaboration, 2016, A&A, 594, A4.
- ↑ Planck 2013 results. VI. High Frequency Instrument Data Processing, Planck Collaboration, 2014, A&A, 571, A6.
- ↑ Planck 2013 results. IX. HFI spectral response, Planck Collaboration, 2014, A&A, 571, A9.
- ↑ The pre-launch Planck Sky Model: a model of sky emission at submillimetre to centimetre wavelengths, J. Delabrouille, M. Betoule, J.-B. Melin, M.-A. Miville-Deschênes, J. Gonzalez-Nuevo, M. Le Jeune, G. Castex, G. de Zotti, S. Basak, M. Ashdown, J. Aumont, C. Baccigalupi, A. Banday, J.-P. Bernard, F. R. Bouchet, D. L. Clements, A. da Silva, C. Dickinson, F. Dodu, K. Dolag, F. Elsner, L. Fauvet, G. Faÿ, G. Giardino, S. Leach, J. Lesgourgues, M. Liguori, J. F. Macias-Perez, M. Massardi, S. Matarrese, P. Mazzotta, L. Montier, S. Mottet, R. Paladini, B. Partridge, R. Piffaretti, G. Prezeau, S. Prunet, S. Ricciardi, M. Roman, B. Schaefer, L. Toffolatti, A&A, 553, A96, (2013).
- ↑ Planck 2013 results. XII. All-sky model of thermal dust emission, Planck Collaboration, 2014, A&A, 571, A12.
- ↑ A simulation pipeline for the Planck mission, M. Reinecke, K. Dolag, R. Hell, M. Bartelmann, T. A. Enßlin, A&A, 445, 373-373, (2006).
- ↑ Making cosmic microwave background temperature and polarization maps with MADAM, E. Keihänen, R. Keskitalo, H. Kurki-Suonio, T. Poutanen, A.-S. Sirviö, A&A, 510, A57+, (2010).
- ↑ Fast Pixel Space Convolution for Cosmic Microwave Background Surveys with Asymmetric Beams and Complex Scan Strategies: FEBeCoP, S. Mitra, G. Rocha, K. M. Górski, K. M. Huffenberger, H. K. Eriksen, M. A. J. Ashdown, C. R. Lawrence, ApJS, 193, 5-+, (2011).
- ↑
Cosmic Microwave background
(Planck) High Frequency Instrument
(Planck) Low Frequency Instrument
Planck Sky Model
Data Processing Center
Attitude History File
analog to digital converter
Sunyaev-Zel'dovich
Early Release Compact Source Catalog
Full-Width-at-Half-Maximum
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
Flexible Image Transfer Specification
Planck Legacy Archive