|
|
| (20 intermediate revisions by 4 users not shown) |
| Line 1: |
Line 1: |
| − | {{DISPLAYTITLE:Internal overall validation}} | + | {{DISPLAYTITLE:Overall internal validation}} |
| | == Overview == | | == Overview == |
| − | Data validation is a step of paramount importance in the complex process of data analysis and the extraction of the final | + | Data validation is critical at each step of the analysis pipeline. Much of the LFI data validation is based on null tests. Here we present some examples from the current release, with comments on relevant time scales and sensitivity to various systematics. In the 2018 release in addition we perform many test to verify the differences between this and previous release (see {{PlanckPapers|planck2016-l02}}). |
| − | scientific goals of an experiment. The LFI approach to data validation is based upon null-tests approach and here we present
| |
| − | the rationale behind envisaged/performed null-tests and the actual results for the present data release. Also we will provide | |
| − | results of the same kind of tests performed on previous release to show the overall improvements in the data quality.
| |
| | | | |
| − | == Null-tests approach == | + | == Null tests approach == |
| − | In general null-tests are performed in order to highlight possible issues in the data related to instrumental | + | Null tests at map level are performed routinely, whenever changes are made to the mapmaking pipeline. These include differences at survey, year, 2-year, half- mission and half-ring levels, for single detectors, horns, horn pairs and full frequency complements. Where possible, map differences are generated in <i>I</i>, <i>Q</i> and <i>U</i>. |
| − | systematic effect not properly accounted for within the processing pipeline and related to known events of the | + | For this release, we use the Full Focal Plane 10 (FFP10) simulations for comparison. We can use FFP10 noise simulations, identical to the data in terms of sky sampling and with matching time domain noise characteristics, to make statistical arguments about the likelihood of the noise observed in the actual data nulls. |
| − | operational conditions (e.g. switch-over of the sorption coolers) or to intrinsic instrument properties coupled with | + | In general null tests are performed to highlight possible issues in the data related to instrumental systematic effecst not properly accounted for within the processing pipeline, or related to known changes in the operational conditions (e.g., switch-over of the sorption coolers), or related to intrinsic instrument properties coupled with the sky signal, such as stray light contamination. |
| − | sky signal like stray-light contamination. | + | Such null-tests can be performed by using data on different time scales ranging from 1 minute to 1 year of observations, at different unit levels (radiometer, horn, horn-pair), within frequency and cross-frequency, both in total intensity, and, when applicable, in polarization. |
| | | | |
| − | Such null-tests are expected to be performed considering data on different time scales ranging from 1-minute to one year
| + | === Sample Null Maps === |
| − | of observations, at different unit level (radiometer, horn, horn-pair, within frequency and cross-frequency both in total
| |
| − | intensity and, when applicable, to polarisation.
| |
| | | | |
| − | This is quite demanding in terms of all possible combinations. In addition some tools are already
| + | [[File:Fig_13.png|thumb|center|900px]] |
| − | available and can be properly used for this kind of analysis. However it may be
| |
| − | possible that on some specific time-scale, detailed tools have to be developed in order
| |
| − | to produce the desired null-test results. In this respect the actual half-ring jack-knives
| |
| − | are suitable to track any effects on pointing period times scales. On time-scales between half-ring
| |
| − | and survey there are lot of possibilities. It has to be verified if the actual code producing
| |
| − | half-ring jack-knives (madam) can handle data producing jack-knives of larger
| |
| − | (e.g. 1 hour) times scales.
| |
| | | | |
| − | It is fundamental that such test have to be performed on DPC data product with clear
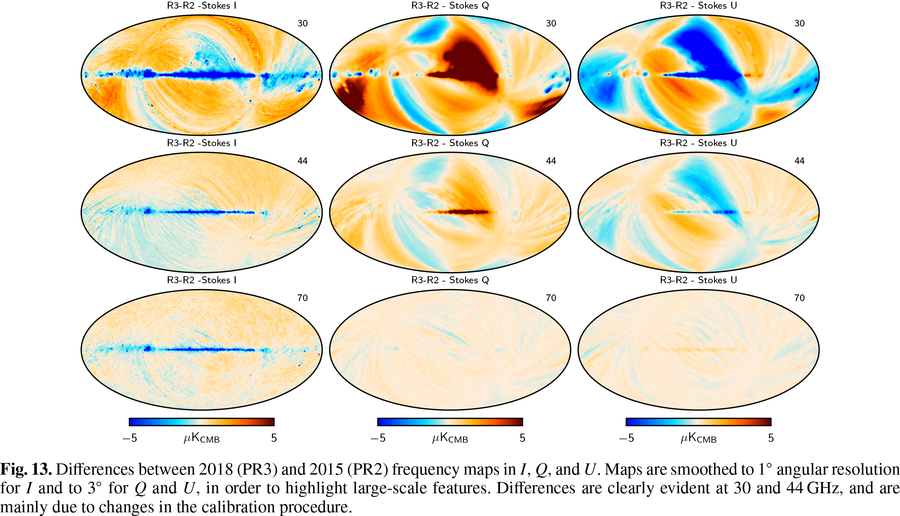
| + | This figure shows difefrences between 2018 and 1015 frequenncy maps in <i>I</i>, <i>Q</i> and <i>U</i>. Large scale differences between the two set of maps are mainly due to changes in the calibration procedure. |
| − | and identified properties (e.g. single <math>R</math>, gains, single fit, etc.) in order to avoid any | |
| − | possible mis-understanding due to usage of non homogeneous data sets.
| |
| | | | |
| − | Many of the null-tests proposed are done at map level with sometime compression of their
| + | [[File:Fig_14.png|thumb|center|900px]] |
| − | statistical information into an angular power spectrum. However
| |
| − | together with full-sky maps it is interesting to have a closer look on some specific sources.
| |
| − | I would be important to compare fluxes from both polarized and un-polarized point sources with
| |
| − | different radiometers in order to asses possible calibration mis-match and/or polarization leakage issues.
| |
| − | Such comparison will also possibly indicate problems related to channel central frequencies.
| |
| − | The proposed set of sources would be: M42, Tau A, Cas A and Cyg A. However other <math>H \, II</math> regions
| |
| − | like Perseus are valuable. One can compare directly their fluxes from different sky surveys and/or the flux
| |
| − | of the difference map and how this is consistent with instrumental noise.
| |
| | | | |
| − | Which kind of effect is probed with a null-test on a specific time scale? Here it is a simple list. At survey time
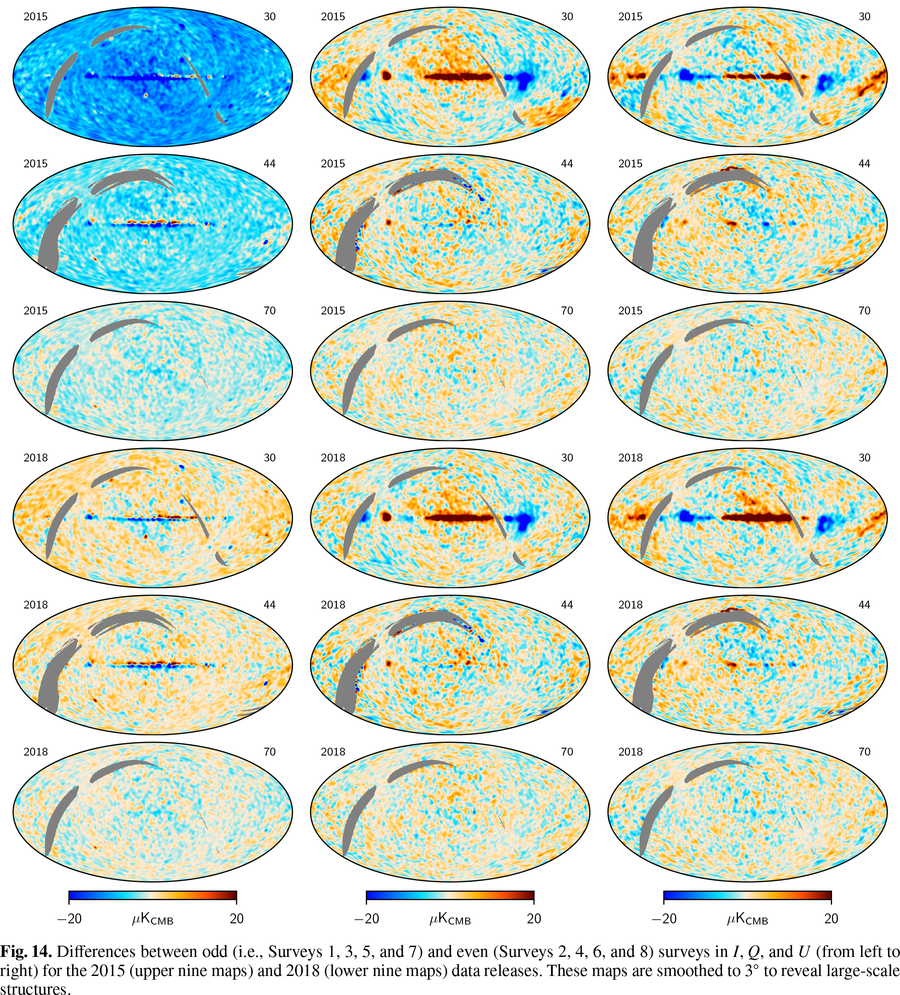
| + | In this figure we consider the set of odd-even survey differences combining all eight sky surveys covered by LFI. These survey combinations optimize the signal-to-noise ratio and highlight |
| − | scale it is possible to underlying any side-lobes effects, while on time scales of full-mission, it is possible to | + | large-scale structures. The nine maps on the left show odd-even survey dfferences for the 2015 release, while the nine maps on the right show the same for the 2018 release. The 2015 data show large residuals in <i>I</i> at 30 and 44 GHz that bias the difference away from zero. This effect is considerably reduced in the 2018 release, as expected from the improvements in the calibration process. The <i>I</i> map at 70 GHz also shows a significant improvement. In the polarization maps, there is a general reduction in the amplitude of structures close to the Galactic plane. |
| − | have an indication of calibration problems when observing the sky with the same S/C orientation. Differences
| |
| − | at this time scale between horns at the same frequency may also reveal central frequency and beam
| |
| − | issues.
| |
| | | | |
| − | === Total Intensity Null Tests ===
| + | [[File:Fig_15.png|thumb|center|400px]] |
| − | In order to highlight different issues, several time scales and data combinations are considered. The following table
| |
| − | is a sort of null-test matrix to be filled with test results. It should be important to try to set a sort
| |
| − | of pass/fail criteria for each of the tests and to be prepared to detailed actions in order to avoid
| |
| − | and correct any failure of the tests. To assess the results an idea could be to proceed as in the nominal pipeline i.e.
| |
| − | to compare the angular power spectra of null test maps with a fiducial angular power spectrum of a white noise map.
| |
| − | This could be made automatic and, in case the test does not pass then a more thorough investigation could be performed.
| |
| − | This will provide an overall indication of the residuals. However structures in the residual are important as well as the
| |
| − | overall average level and visual inspection of the data is therefore fundamental.
| |
| | | | |
| − | Concerning null-tests on various time scales a comment is in order. At large time scales (i.e. of the order of
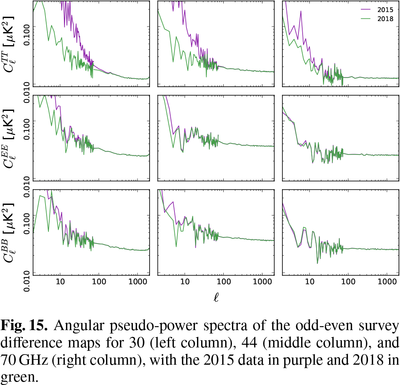
| + | Finally here we shows pseudo-angular power spectra from the oddeven survey dfferences. There is great improvement in 2018 in removing largescale structures at 30 GHz in <i>TT</i>, <i>EE</i>, and somewhat in <i>BB</i>, and also in <i>TT</i> at 44 GHz. |
| − | a survey or more) it is clear that the basic data set will be made of the single survey maps at
| |
| − | radiometer/horn/frequency level that will be properly combined to obtain the null-test under consideration.
| |
| − | For example at 6 months time scale we will analysis maps of the difference between different surveys
| |
| − | for the radiometer/horn/frequency under test. On the other hand at 12 months time scale we will combine
| |
| − | surveys 1 and 2 together to be compared with the same combination for surveys 3 and 4.
| |
| − | At full-mission time scale, the analysis it is not always possible e.g. at radiometer level we have only one
| |
| − | full-mission data set. However it would be interesting to combine odd surveys together and compare them
| |
| − | with even surveys again combined together.
| |
| − | On shorter time scales (i.e. less than a survey) the data products to be considered are different and
| |
| − | will be the output of the jack-knives code when different time scales are considered: the usual half-ring
| |
| − | JK on pointing period time scale and the new, if possible, jack-knives on 1 minute time scale.
| |
| − | Therefore null-tests will use both surveys/full-mission maps as well as tailored jack-knives maps.
| |
| | | | |
| − | The following table reports our total intensity null-tests matrix with a <math>\checkmark</math> where tests are possible.
| |
| − | {| border="1" cellpadding = "5" cellspacing = "0" align = "centre"
| |
| − | |-
| |
| − | ! Data Set
| |
| − | ! 1minute
| |
| − | ! 1 hour
| |
| − | ! Survey
| |
| − | ! Full Mission
| |
| − | |-
| |
| − | | Radiometer (M/S) || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Horn (M+S) || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Horn Pair<math>^1</math> || || || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Frequency || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Cross-Frequency || || || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |}
| |
| − | <math>^1</math> this is <math>(M+S)/2</math> and differences are between couple of horns (e.g. (28M+28S)/2- (27M+27S)/2)
| |
| | | | |
| − | === Polarisation Null Tests === | + | ===Intra-frequency consistency check=== |
| − | The same arguments applies also for polarization analysis with only some differences regarding the possible
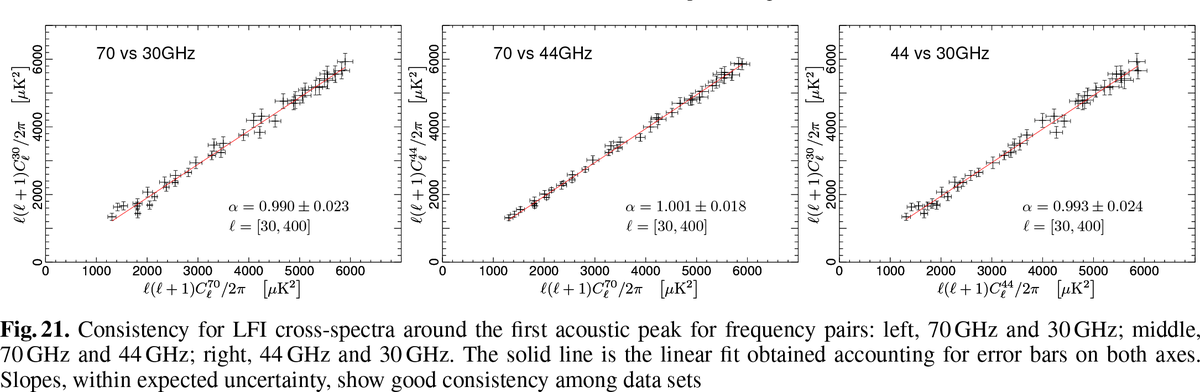
| + | We have tested the consistency between 30, 44, and 70GHz maps by comparing the power spectra in the multipole range around the first acoustic peak. In order to do so, we have removed the estimated contribution from unresolved point source from the spectra. We have then built scatter plots for the three frequency pairs, i.e., 70GHz versus 30 GHz, 70GHz versus 44GHz, and 44GHz versus 30GHz, and performed a linear fit, accounting for errors on both axes. |
| − | combination producing polarized data. Radiometer will not be available, instead of sum between M and S radiometer we will
| + | The results reported below show that the three power spectra are consistent within the errors. Moreover, note that the current error budget does not account for foreground removal, calibration, and window function uncertainties. Hence, the observed agreement between spectra at different frequencies can be considered to be even more satisfactory. |
| − | consider their difference.
| |
| | | | |
| − | {| border="1" cellpadding = "5" cellspacing = "0" align = "centre"
| + | [[File:Fig_21.png|thumb|center|1200px]] |
| − | |-
| |
| − | ! Data Set
| |
| − | ! 1minute
| |
| − | ! 1 hour
| |
| − | ! Survey
| |
| − | ! Full Mission
| |
| − | |-
| |
| − | | Horn (M-S) || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Horn Pair<math>^1</math> || || || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Frequency || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |-
| |
| − | | Cross-Frequency || || || <math>\checkmark</math> || <math>\checkmark</math>
| |
| − | |}
| |
| − | <math>^1</math> this is difference between couple of horns (e.g. (28M-28S)/2- (27M-27S)/2)
| |
| | | | |
| − | === Practical Considerations ===
| |
| − | For practical purposed and visual inspection of the null-tests results it would be useful to produce results smoothed at <math>3^\circ</math> (and at <math>10^\circ</math> for highlight larger angular scales) for
| |
| − | all the total intensity maps. For polarization, as we already did several times when comparing to <math>WMAP</math> data,
| |
| − | a downgrade of the product at <math>N_{\rm side}=128</math> would be useful to highlight large scale residuals. These considerations are
| |
| − | free to evolve according to our needs.
| |
| − |
| |
| − | Due to large possibilities and number of data sets to be considered, it would be desirable to have sort of automatic tools that
| |
| − | ingest two, or more, inputs maps and produce difference map(s) and corresponding angular power spectrum(spectra). This
| |
| − | has been implemented using Python language and interacting directly with FITS files of a specific data release. The code is
| |
| − | parallel and can run both at NERSC and at DPC producing consistent results. In addition for each null-tests performed a JSON
| |
| − | DB file is produced in which main test informations are stored together with interesting computed quantities like mean, standard deviation of the residual maps. Beside JSON files also GIF images of the null-test are produced. Such JSON and GIF files are used to create (both with Python again and with Scheme) a report in form of an HTML page from the LFI Wiki.
| |
| − |
| |
| − | Together with images, power spectra of the residual are also produced and compared with the expected level of white noise
| |
| − | derived from the half-ring jack-knifes. With these quantities are combined to produce a sort of <math>\chi^2</math>. This gives an indication of the deviation of the residuals with respect to the white noise level. Of course underlying signal does not posses a Gaussian statistic and therefore with non-Gaussian data, the <math>\chi^2</math> tests is less meaningful. However this gives an hint on the presence of residuals which in some cases are indeed expected: in fact making difference between odd and even survey at horn and frequency level, is a way to show the signature of the external stray-light which, although properly accounted for during the calibration procedure, has not been removed from the data.
| |
| − |
| |
| − | ==Consistency checks ==
| |
| − |
| |
| − | All the details can be found in {{PlanckPapers|planck2013-p02}} {{PlanckPapers|planck2014-a03||Planck-2015-A03}}.
| |
| − |
| |
| − | ===Intra frequency consistency check===
| |
| − | We have tested the consistency between 30, 44, and 70 GHz maps by comparing the power spectra in the multipole range around the first acoustic peak. In order to do so, we have removed the estimated contribution from unresolved point source from the spectra. We have then built the scatter plots for the three frequency pairs, i.e. 70 vs 30 GHz, 70 vs 44 GHz, and 44 vs 30 GHz, and performed a linear fit accounting for errors on both axis.
| |
| − | The results reported in Fig. 1 show that the three power spectra are consistent within the errors. Moreover, please note that current error budget does not account for foreground removal, calibration, and window function uncertainties. Hence, the resulting agreement between spectra at different frequencies can be fairly considered even more significant.
| |
| − |
| |
| − | [[File:LFI_70vs44_DX11D_maskTCS070vs060_a.jpg|thumb|center|400px|]][[File:LFI_70vs30_DX11D_maskTCS070vs040_a.jpg|thumb|center|400px|]][[File:LFI_44vs30_DX11D_maskTCS060vs040_a.jpg|thumb|center|400px|'''Figure 1. Consistency between spectral estimates at different frequencies. From top to bottom: 70 vs 44 GHz; 70 vs 30 GHz; 44 vs 30 GHz. Solid red lines are the best fit of the linear regressions, whose angular coefficients <math>\alpha</math> are consistent with 1 within the errors.''']]
| |
| | | | |
| | ===70 GHz internal consistency check=== | | ===70 GHz internal consistency check=== |
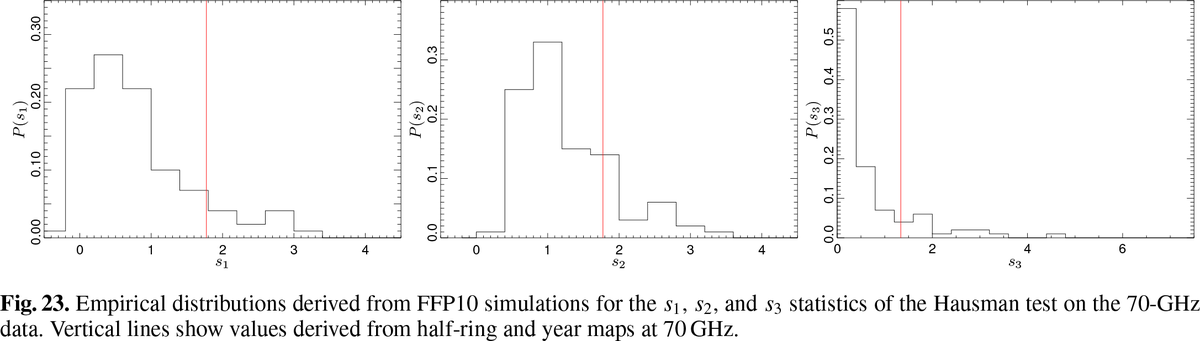
| − | We use the Hausman test {{BibCite|polenta_CrossSpectra}} to assess the consistency of auto and cross spectral estimates at 70 GHz. We define the statistic: | + | We use the Hausman test {{BibCite|polenta_CrossSpectra}} to assess the consistency of auto- and cross-spectral estimates at 70 GHz. We specifically define the statistic: |
| | | | |
| | :<math> | | :<math> |
| − | H_{\ell}=\left(\hat{C_{\ell}}-\tilde{C_{\ell}}\right)/\sqrt{Var\left\{ \hat{C_{\ell}}-\tilde{C_{\ell}}\right\} } | + | H_{\ell}=\left(\hat{C_{\ell}}-\tilde{C_{\ell}}\right)/\sqrt{{\rm Var}\left\{ \hat{C_{\ell}}-\tilde{C_{\ell}}\right\} }, |
| | </math> | | </math> |
| | | | |
| − | where <math>\hat{C_{\ell}}</math> and <math>\tilde{C_{\ell}}</math> represent auto- and | + | where <math>\hat{C_{\ell}}</math> and <math>\tilde{C_{\ell}}</math> represent auto- and |
| − | cross-spectra respectively. In order to combine information from different multipoles into a single quantity, we define the following quantity: | + | cross-spectra, respectively. In order to combine information from different multipoles into a single quantity, we define |
| | | | |
| | :<math> | | :<math> |
| − | B_{L}(r)=\frac{1}{\sqrt{L}}\sum_{\ell=2}^{[Lr]}H_{\ell},r\in\left[0,1\right] | + | B_{L}(r)=\frac{1}{\sqrt{L}}\sum_{\ell=2}^{[Lr]}H_{\ell},r\in\left[0,1\right], |
| | </math> | | </math> |
| | | | |
| − | where <math>[.]</math> denotes integer part. The distribution of <math>B_{L}(r)</math> | + | where square brackets denote the integer part. The distribution of <i>B<sub>L</sub></i>(<i>r</i>) |
| | converges (in a functional sense) to a Brownian motion process, which can be studied through the statistics | | converges (in a functional sense) to a Brownian motion process, which can be studied through the statistics |
| − | <math>s_{1}=\textrm{sup}_{r}B_{L}(r)</math> | + | <i>s</i><sub>1</sub>=sup<sub><i>r</i></sub><i>B<sub>L</sub></i>(<i>r</i>), |
| − | <math>s_{2}=\textrm{sup}_{r}|B_{L}(r)|</math> and | + | <i>s</i><sub>2</sub>=sup<sub><i>r</i></sub>|<i>B<sub>L</sub></i>(<i>r</i>)|, and |
| − | <math>s_{3}=\int_{0}^{1}B_{L}^{2}(r)dr</math>. Using the ''FFP7'' simulations | + | <i>s</i><sub>3</sub>=∫<sub>0</sub><sup>1</sup><i>B<sub>L</sub></i><sup>2</sup>(<i>r</i>)dr. Using the "FFP10" simulations, |
| − | we derive the empirical distribution for all the three test statistics and we compare with results obtained from Planck data | + | we derive empirical distributions for all the three test statistics and compare with results obtained from Planck data. We find that the Hausman test shows no statistically significant inconsistencies between the two spectral |
| − | (see Fig. 2). Thus, the Hausman test shows no statistically significant inconsistencies between the two spectral
| |
| | estimates. | | estimates. |
| | | | |
| − | [[File:cons2.jpg|thumb|center|800px|'''Figure 2. From left to right, the empirical | + | [[File:Fig_23.png|thumb|center|1200px|]] |
| − | distribution (estimated via ''FFP7'') of the <math>s_{1},s_{2},s_{3}</math>
| |
| − | statistics (see text). The vertical line represents 70 GHz data.''']]
| |
| − | | |
| − | As a further test, we have estimated the temperature power spectrum for each of three horn-pair map, and we have compared the
| |
| − | results with the spectrum obtained from all the 12 radiometers shown above. In Fig. 3 we show the
| |
| − | difference between the horn-pair and the combined power spectra.
| |
| − | Again, the error bars have been estimated from the ''FFP7'' simulated dataset. A <math>\chi^{2}</math> analysis of the residual shows that they are compatible with the null hypothesis, confirming the
| |
| − | strong consistency of the estimates.
| |
| − | | |
| − | [[File:cons3.jpg|thumb|center|500px|'''Figure 3. Residuals between the auto power spectra of the horn pair maps and the power spectrum of the full 70 GHz frequency map. Error bars are derived from ''FFP7'' simulations.''']]
| |
| | | | |
| | <!-- | | <!-- |
Overview[edit]
Data validation is critical at each step of the analysis pipeline. Much of the LFI data validation is based on null tests. Here we present some examples from the current release, with comments on relevant time scales and sensitivity to various systematics. In the 2018 release in addition we perform many test to verify the differences between this and previous release (see Planck-2020-A2[1]).
Null tests approach[edit]
Null tests at map level are performed routinely, whenever changes are made to the mapmaking pipeline. These include differences at survey, year, 2-year, half- mission and half-ring levels, for single detectors, horns, horn pairs and full frequency complements. Where possible, map differences are generated in I, Q and U.
For this release, we use the Full Focal Plane 10 (FFP10) simulations for comparison. We can use FFP10 noise simulations, identical to the data in terms of sky sampling and with matching time domain noise characteristics, to make statistical arguments about the likelihood of the noise observed in the actual data nulls.
In general null tests are performed to highlight possible issues in the data related to instrumental systematic effecst not properly accounted for within the processing pipeline, or related to known changes in the operational conditions (e.g., switch-over of the sorption coolers), or related to intrinsic instrument properties coupled with the sky signal, such as stray light contamination.
Such null-tests can be performed by using data on different time scales ranging from 1 minute to 1 year of observations, at different unit levels (radiometer, horn, horn-pair), within frequency and cross-frequency, both in total intensity, and, when applicable, in polarization.
Sample Null Maps[edit]
This figure shows difefrences between 2018 and 1015 frequenncy maps in I, Q and U. Large scale differences between the two set of maps are mainly due to changes in the calibration procedure.
In this figure we consider the set of odd-even survey differences combining all eight sky surveys covered by LFI. These survey combinations optimize the signal-to-noise ratio and highlight
large-scale structures. The nine maps on the left show odd-even survey dfferences for the 2015 release, while the nine maps on the right show the same for the 2018 release. The 2015 data show large residuals in I at 30 and 44 GHz that bias the difference away from zero. This effect is considerably reduced in the 2018 release, as expected from the improvements in the calibration process. The I map at 70 GHz also shows a significant improvement. In the polarization maps, there is a general reduction in the amplitude of structures close to the Galactic plane.
Finally here we shows pseudo-angular power spectra from the oddeven survey dfferences. There is great improvement in 2018 in removing largescale structures at 30 GHz in TT, EE, and somewhat in BB, and also in TT at 44 GHz.
Intra-frequency consistency check[edit]
We have tested the consistency between 30, 44, and 70GHz maps by comparing the power spectra in the multipole range around the first acoustic peak. In order to do so, we have removed the estimated contribution from unresolved point source from the spectra. We have then built scatter plots for the three frequency pairs, i.e., 70GHz versus 30 GHz, 70GHz versus 44GHz, and 44GHz versus 30GHz, and performed a linear fit, accounting for errors on both axes.
The results reported below show that the three power spectra are consistent within the errors. Moreover, note that the current error budget does not account for foreground removal, calibration, and window function uncertainties. Hence, the observed agreement between spectra at different frequencies can be considered to be even more satisfactory.
70 GHz internal consistency check[edit]
We use the Hausman test [2] to assess the consistency of auto- and cross-spectral estimates at 70 GHz. We specifically define the statistic:
- [math]
H_{\ell}=\left(\hat{C_{\ell}}-\tilde{C_{\ell}}\right)/\sqrt{{\rm Var}\left\{ \hat{C_{\ell}}-\tilde{C_{\ell}}\right\} },
[/math]
where [math]\hat{C_{\ell}}[/math] and [math]\tilde{C_{\ell}}[/math] represent auto- and
cross-spectra, respectively. In order to combine information from different multipoles into a single quantity, we define
- [math]
B_{L}(r)=\frac{1}{\sqrt{L}}\sum_{\ell=2}^{[Lr]}H_{\ell},r\in\left[0,1\right],
[/math]
where square brackets denote the integer part. The distribution of BL(r)
converges (in a functional sense) to a Brownian motion process, which can be studied through the statistics
s1=suprBL(r),
s2=supr|BL(r)|, and
s3=∫01BL2(r)dr. Using the "FFP10" simulations,
we derive empirical distributions for all the three test statistics and compare with results obtained from Planck data. We find that the Hausman test shows no statistically significant inconsistencies between the two spectral
estimates.
References[edit]
- ↑ Planck 2018 results. II. Low Frequency Instrument data processing, Planck Collaboration, 2020, A&A, 641, A2.
- ↑ Unbiased estimation of an angular power spectrum, G. Polenta, D. Marinucci, A. Balbi, P. de Bernardis, E. Hivon, S. Masi, P. Natoli, N. Vittorio, J. Cosmology Astropart. Phys., 11, 1, (2005).