The Planck mission
Contents
[hide]Introduction[edit]
Planck is a space telescope of the European Space Agency designed to answer key cosmological questions. Its main goal is to determine the geometry and content of the Universe, and which theories describing the birth and evolution of the Universe are correct. To achieve this ambitious objective, it observed the Cosmic Microwave Background radiation (CMB), emitted about 14 billion years ago, just over 300,000 years after the Big Bang. Today the CMB permeates the Universe and is observed to have an average temperature of 2.7 K. Small deviations from this average value (the so-called anisotropies), observable at angular scales larger than ∼5 arcminutes, encode a wealth of information on the properties of the Universe in its infancy. The objective of Planck is to measure these properties with an unprecedented accuracy and level of detail.
As with all ESA scientific missions, Planck was developed in a partnership with the European scientific community. Two consortia of scientific institutes, each led by a Principal Investigator, developed and delivered to ESA two instruments designed specifically for Planck. Each of these instruments targets a specific number of wavelength bands within the range in which the CMB is observable. Together, the two instruments are capable of collecting data of a quality adequate to measure the CMB signal and distinguish it from other confusing sources. A large telescope collects the light from the sky and deliver it to the instruments for measurement and analysis. The reflectors of the Planck telescope were developed and delivered to ESA by a Danish consortium of institutes. ESA retains overall management of the project, develops and procures the spacecraft, integrates the instruments into the spacecraft, and launches and operates it. Planck was launched on May 14th 2009 on an Ariane 5 rocket together with the Herschel Space Observatory. After launch, they were both placed into orbits around the L2 Lagrange of the Sun-Earth system, located about 1.5 million km from the Earth. From that far vantage point, Planck sweeped the sky regularly in large swaths, and covered it fully about six times. Each of the two instrument consortia operated their respective instrument and processed all the data into usable scientific products. At the end of the mission the consortia delivered the final products to ESA, which archives them and distributes them to the community.
Early operations and transfer to orbit[edit]
Planck was launched from the Centre Spatial Guyanais in Kourou (French Guyana) on 14 May 2009 at its nominal lift-off time of 13:12 UT, on an Ariane 5 ECA rocket of Arianespace2. ESA’s Herschel observatory was launched on the same rocket. At 13:37:55 UT, Herschel was released from the rocket at an altitude of 1200 km; Planck followed suit at 13:40:25UT. The separation attitudes of both satellites were within 0.1 deg. of prediction. The Ariane rocket placed Planck with excellent accuracy (semimajor axis within 1.6 % of prediction), on a trajectory towards the second Lagrangian point of the Earth-Sun system (L2) . The orbit describes a Lissajous trajectory around L2 with a ∼6 month period that avoids crossing the Earth penumbra for at least 4 years.
After release from the rocket, three large manoeuvres were carried out to place Planck in its intended final orbit. Once in its final orbit, very small manoeuvres are required at approximately monthly intervals (1 ms−1 per year) to keep Planck from drifting away from its intended path around L2. The attitude manoeuvres required to followthe scanning strategy require about 2.6 ms−1 per year. Overall, the excellent performance of launch and orbit manoeuvres will lead to a large amount (∼160 kg, or ∼40% of initial tank loading) of fuel remaining on board at end of mission operations.
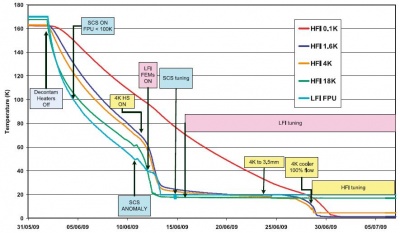
Planck started cooling down radiatively shortly after launch. Heaters were activated to hold the focal plane at 250 K, which was reached around 5 h after launch. The valve opening the exhaust piping of the dilution cooler was activated at 03:30 UT, and the 4He-JT cooler compressors were turned on at low stroke at 05:20 UT. After these essential operations were completed, on the second day after launch, the focal plane temperature was allowed to descend to 170 K for out-gassing and decontamination of the telescope and focal plane.
Commissioning and initial science operations[edit]
Commissioning[edit]
The first period of operations focussed on commissioning activities, i.e., functional check-out procedures of all sub-systems and instruments of the Planck spacecraft in preparation for running science operations related to calibration and performance verification of the payload. Planning for commissioning operations was driven by the telescope decontamination period of 2 weeks and the subsequent cryogenic cool-down of the payload and instruments. The overall duration of the cool-down was approximately 2 months, including the decontamination period. The commissioning activities were executed very smoothly and all sub-systems were found to be in good health. The commissioning activities were formally completed at the time when the HFI bolometer stage reached its target temperature of 100 mK, on 3 July 2009 at 01:00 UT. At this time all the critical resource budgets (power, fuel, lifetime, etc.) were found to contain very significant margins with respect to the original specification.
Calibration and performance verification[edit]
Calibration and performance verification (CPV) activities started during the cool-down period and continued until the end of August 2009. On completion of all the planned activities, it was concluded that the two instruments were fully tuned and ready for routine operations. No further parameter tuning was expected to be needed, except for the sorption cooler, which requires a weekly change in operational parameters. The scientific performance parameters of both instruments was in most respects as had been measured on the ground before launch. The only significant exception was that, due to the high level of Galactic cosmic rays, the bolometers of HFI were detecting a higher number of glitches than expected, causing a modest (∼10%) level of systematic effects on their noise properties. The satellite did not introduce any major systematic effects into the science data. In particular, the telemetry transponder did not result in radio-frequency interference, which implies that the data acquired during visibility periods is useable for science.
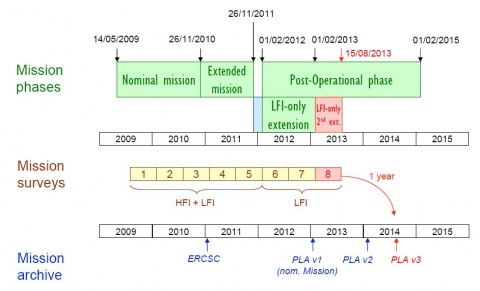
First-Light Survey[edit]
The First Light Survey (FLS) was the last major activity planned before the start of routine surveying of the sky. It was conceived as a two-week period during which Planck would be fully tuned up and operated as if it was in its routine phase. This stable period could have resulted in the identification of further tuning activities required to optimise the performance of Planck in the long-duration surveys to come. The FLS was conducted between 13 and 27 August, and in fact led to the conclusion that the Planck payload was operating stably and optimally, and required no further tuning of its instruments. Therefore the period of the FLS was accepted as a valid part of the first Planck survey.
Routine operations phase[edit]
The routine operations phase of Planck is characterised by continuous and stable scanning of the sky and data acquisition by LFI and HFI. It started with the FLS on 13 August of 2009, at 14:15 UT.
The Planck satellite generates (and stores on-board) data continuously at the following typical rates: 21 kilobit s−1 (kbps) of house-keeping (HK) data from all on-board sources, 44 kbps of LFI science data and 72 kbps of HFI science data. The data are brought to ground in a daily pass of approximately 3 h duration. Besides the data downloads, the passes also acquire realtime HK and a 20 min period of real-time science (used to monitor instrument performance during the pass). Planck utilises the two ESA deep-space ground stations in New Norcia (Australia) and Cebreros (Spain), usually the former. Scheduling of the daily telecommunication period is quite stable, with small perturbations due to the need to coordinate the use of the antenna with other ESA satellites (in particular Herschel). At the ground station the telemetry is received by redundant chains of front-end/back-end equipment. The data flows to the mission operations control centre (MOC) located at ESOC in Darmstadt (Germany), where it is processed by redundant mission control software (MCS) installations and made available to the science ground segment. To reduce bandwidth requirements between the station and ESOC only one set of science telemetry is usually transferred. Software is run post-pass to check the completeness of the data. This software check is also used to build a catalogue of data completeness, which is used by the science ground segment to control its own data transfer process. Where gaps are detected, attempts to fill them are made as an offline activity (normally next working day), the first step being to attempt to reflow the relevant data from station. Early in the mission these gaps were more frequent, with some hundreds of packets affected per week (impact on data return of order 50 ppm) due principally to a combination of software problems with the data ingestion and distribution in the MCS, and imperfect behaviour of the software gap check. Software updates implemented during the mission have improved the situation such that gaps are much rarer, with a total impact on data return well below 1 ppm. Redump of data from the spacecraft is attempted when there have been losses in the space link. This has only been necessary on three occasions. In each case the spacecraft redump has successfully recovered all the data.
All the data downloaded from the satellite, and processed products such as filtered attitude information, are made available each day for retrieval from the MOC by the LFI and HFI Data Processing Centres (DPCs).
The scanning strategy is the following: the spin axis follows a cycloidal path on the sky by step-wise displacements of 2 arcmin approximately every 50 min. The dwell time (i.e., the duration of stable data acquisition at each pointing) has varied sinusoidally by a factor of ∼2. Planck’s scanning strategy results in significantly inhomogeneous depth of integration time across the sky; the areas near the ecliptic poles are observed with greater depth than all others.
The scanning strategy for the second year of Routine Operations (i.e., Surveys 3 and 4) is exactly the same as for the first year, except that all pointings are shifted by 1 arcmin along the cross-scanning direction, in order to provide finer sky sampling for the highest frequency detectors when combining two years of observations.
Orbit maintenance manoeuvres were carried out at approximately monthly intervals6. Although the manoeuvres only required a few minutes, preparations, post-manoeuvre massproperty calibration, and re-entry into scientific slewing mode increased the overhead to several hours. The manoeuvres were carried out without disturbing the path of the spin axis from its nominal scanning law. The dwell times of pointings before and after the execution of the manoeuvre were reduced to allow all pre-planned pointings to be carried out.
While the Planck detectors are scanning the sky, they also naturally observe celestial calibrators. The main objects used for this purpose are the Crab Nebula, and the bright planets Mars, Jupiter and Saturn.
Payload performance[edit]
The main achievements in terms of payload performance are the following:
- the angular resolution measured on planets is within a few per cent of that predicted on the ground
- the instantaneous sensitivity of the Planck LFI and HFI channels is estimated to be approximately 10% larger than that measured on the ground and extrapolated to launch conditions
- the photometric calibration uncertainty quoted is conservatively based on the current knowledge of systematic effects and data processing pipelines. There is no reason to believe that the mission goals (1% in CMB channels and 3% at the highest frequencies) will not be reached for all Planck channels in due time.
For more information[edit]
A complete overview of the Planck mission and its science programme can be found in the Blue Book [[1]].
More details on the Planck mission performance can be found in #planck2011-1-1, Planck early paper I .
A complete list of Planck publications can be found here [2].
References[edit]
<biblio force=false>
</biblio>
Cosmic Microwave background
European Space Agency
(Planck) High Frequency Instrument
Calibration and Performance Verification
(Planck) Low Frequency Instrument
House Keeping
[ESA's] Mission Operation Center [Darmstadt, Germany]
European Space Operations Centre (Darmstadt)