TOI processing

Overview

The LFI Level 2 Pipeline analyses data from each horn of the instrument separately, one pointing period at a time, and stores the results in an object the length of an OD. Each diode of the horn is corrected for systematic effects. Next, measurements of the sky and the 4-K load are differenced, then the signals from one diode are combined with signals from the complementary diode in the same radiometer. Finally, photometric calibration is applied for each horn.

Pre-processing

Before the Level 2 pipeline is run, the Mission information and data sampling divisions are stored in the database, in order to improve the analysis.

The Mission information is a set of objects, one for each Operational Day (OD, as defined in the glossary), in which are stored pointing period data: the DPC pointing ID (where 1 is the first pointing of the nominal mission); PSO pointing ID; start OBT of the pointing manoeuvre; start OBT of the stable pointing period; OBT of the end of the stable pointing period; and spin axis ecliptic longitude and latitude.

The sampling information is a set of objects, one for each LFI frequency, in which are stored for each pointing ID: the start OBT of the pointing manoeuvre; th start OBT of the stable pointing period; the end OBT of the pointing period; the number of samples of the pointing, number of stable samples of the pointing; the starting sample of the stable pointing period; and the sample number from the start of the nominal mission. Valid samples and OBTs are defined to be those where any of the radiometers in a frequency band contain valid data.

ADC correction

During the analysis of LFI date, a systematic effect was discovered that was common to both white noise and calibration. This turned out to be a nonlinearity in the analogue-to-digital converter (ADC) on board, as discussed further in Planck-2013-II, Planck-2013-III, Planck-2015-A03, Planck-2015-A04 and Planck-2020-A2.

Evaluation

The mathematical model represents the digital ADC output as:

[math] X = (V - \Delta) \gamma + x_0 [/math],

where V is the voltage input, γ is the DAE gain, Δ is the DAE offset and x₀ is the DAE T_zero.

We can model the non-linearity as a function of the input voltage R(V). So we have the apparent inferred voltage V' and we can link it to the actual input voltage with:

[math] \{(V - \Delta) \gamma + x_0\} R(V) = X' = (V' - \Delta) \gamma + x_0 [/math],

so that

[math] R(V) = (V' - \Delta) \gamma + x_0 \over (V - \Delta) \gamma + x_0 [/math].

Since V >> Δ and V γ >> x₀, we can use the much simpler relation

[math] R(V) = \frac{V'}{V} [/math],

and we expect this to be very near to unity for all V.

To find the response curve we have only the apparent voltage to work with, so we had to use the inverse response function R'(V') and replace the real input voltage with T_sys times the time varying gain factor G(t):

[math] V = V'R'(V') = G(t)T_{\rm sys} [/math].

If we introduce a small signal on top of T_sys, which leads to increased detected voltage and corresponding apparent voltage increment, then

[math] V + \delta V = (V' + \delta V')\,R' (V' + \delta V') = G(t) (T_{\rm sys} + \delta T) [/math],

so carrying out the differentiation with respect to V' of the relation between true and apparent signal voltage leads to

[math] \delta V = \left\{ V' {dR'(V') \over dV'} + R'(V') \right\} \delta V' = G(t) \delta T [/math].

We now assume T_sys and δT are fixed and that the variations are due to slow drifts in the gain. Then we can isolate the terms

[math] V' = {G(t) T_{\rm sys} \over R'(V')} [/math],

[math] \delta V' = {G(t) \delta T \over V' {dR'(V') \over dV} + R'(V')} [/math].

Combining the equations to remove the gain factor, we have

[math] {V' R'(V') \over T_{\rm sys}} = {\delta V' \left\{{V'dR'(V') \over dV'} + R'(V')\right\} \over \delta T } [/math].

Rearranging and setting a = δT/T_sys gives

[math] {dR'(V') \over dV' } = \left( {a V'\over \delta V'} - {1 \over V'} \right) R'(V') [/math].

We see the expected direct proportionality of δV' to V', based on the assumption that the variations in voltage are due to overall gain drift, so that the amplitude of voltage and signal will vary together. Then there is the additional differential term, which will pull the signal amplitude away from the linear relationship. So if we plot measured white noise or dipole gain factor against recovered voltage, we should see a linear curve with variations due to local slope changes at particular voltages. The linear part can be taken out and the differential part fitted. This was numerically integrated to obtain the inverse response curve, which is then used to convert the measured voltages to corrected voltages.

Application

In the 2015 release we fit white noise amplitudes binned with respect to detector voltage with a simple spline curve and we translate results into a correction curve as described in Planck-2015-A03. Instead, the fit now relies on a more physically motivated function based on voltage steps (see Planck-2020-A2 for futher details). We compared the results between this method and the previous one by means of null-maps, checking the consistency of the resulting new gain solution with the new ADC correction applied. This was done by computing the rms scatter from the 8 different survey maps taking into account pixel hits and zero levels. A ``goodness" parameter can then be derived from the mean level of the masked null-map made between these survey scatter maps. The 70 and 44 GHz null-maps failed to show significant improvements but this was not the case at 30 GHz. Inspecting the ADC solutions it became clear that the higher noise per radiometer and low ADC non-linearity at 70 GHz did not allow for a good fit. Meanwhile the ADC effect was so large at 44 GHz that new model could not reproduce some of the details, and so led to some small residuals. The 30 GHz system has much lower noise and less thermal drift in the gain, meaning that more voltage levels were revisited more often thus yielding a more consistent ADC model curve. It was therefore decided to keep this new solution only for the 30 GHz channels. The other two channels thus have the same correction for ADC non-linearity as in the previous release.

Spike removal

Some of the LFI receivers exhibit a small artefact with exactly 1-s period, that produces effects visible in the power spectra. The effect is a set of spikes at 1 Hz and harmonics. The spurious signal can be well modelled and is removed from the timelines. More information can be found in Planck-2013-II, Planck-2013-III, Planck-2015-A03, Planck-2015-A04 and Planck-2020-A2.

Modelling

The cause of the spikes at 1 Hz and harmonics is a tiny 1-s square-wave embedded in signals from the affected channels. The method used to estimate the 1-Hz signal is to build a template in the time domain, synchronized with the spurious signal. The first step is to divide each second of data into time bins using OBT. The number of bins is computed using

[math] N_{\rm bins} = f_{\rm samp} \times template\_resolution[/math]

where f_samp is the sampling frequency and is 136 Hz at 70 GHz, 80 at 44 GHz, and 56 at 30 GHz. Then the vector of bins is initialized with time intervals. To avoid aliasing effects, the template resolution is √3. We can write the process adding indices to the time sample; here a lower index denotes the particular time sample, while the upper index labels the bin into which the sample falls. The linear filter can be written as

[math] s(t_{i}^{j}) = a_j \left\{1- \Delta x (t_{i}^{j}) \right\} + a_{j+1} \Delta x (t_{i}^{j})[/math].

Here Δx(t_i) is the filter weight, which is determined by where the sample lies within the bin. If we use t^j with only an upper index to denote the start of each bin, then we can write the filter weight as

[math] \Delta x (t_{i}^{j}) = {{{t_i^j - t^j} \over {t^{j+1} - t^j}}} [/math].

In other words, the filter weight is the time sample value minus the start of the bin divided by the width of the bin.

We must estimate the parameters a_j from the data. With the assumption that the instrument has stable noise properties, we can use a least squares algorithm to estimate the bin values:

[math] {\partial \over \partial a_k} \sum_{i,j} \left( s(t_i^j) – d_i^j \right)^2 = 0 [/math].

This can be represented in the matrix equation

[math] {\sf M}_{jk}a_k = b_j [/math],

with the following definitions:

[math] {\sf M}_{k,k-1} = \sum_i \left\{1 - \Delta x (t_i^{k-1})\right\} \Delta x (t_i^{k-1}) [/math];

[math] {\sf M}_{k,k} = \sum_i \left\{1 - \Delta x (t_i^k)\right\}^2 \Delta x (t_i^{k-1})^2 [/math];

[math] {\sf M}_{k,k+1} = \sum_i \left\{1 - \Delta x (t_i^k)\right\} \Delta x (t_i^k) [/math];

[math] {\sf M}_{k,k+n} (|n| \gt 1) = 0 [/math];

[math] b_j = \sum_i d_i^k \left\{1- \Delta x (t_k^i)\right\} + d_i^{k-1}\Delta x (t_i^{k-1}) [/math].

With these definitions we have to make use of periodic boundary conditions to obtain the correct results, such that if k = 0, then k-1 = n-1 and if k = n-1, then k+1 = 0. Once this is done, we have a symmetric tridiagonal matrix with additional values at the upper right and lower left corners. The matrix can be solved with LU decomposition. In order to be certain of the numerical accuracy of the result, we can perform a simple iteration. The solving of the linear system and the iterative improvement of the solution are implemented as suggested in Numerical Recipes (Press et al., Cambridge University Press, 2007).

Application

For each of the 44 LFI diodes there is a corresponding object in the Database. After studying the amplitude of the spikes at other LFI frequencies, we chose to apply the correction only to the 44 GHz radiometers. Each object contains three columns: the bins start time vector; the sky amplitudes; and the reference amplitudes.

For each sample the value to be subtracted is computed using

[math] V = A^{\rm sky}_k (1 - \Delta x (t_k)) + A^{\rm sky}_{k+1} \Delta x (t_k) [/math],

where k is the index of the bins at a given time.

Filling gaps in the data

During the mission, a small number of data packets were lost (Planck-2013-II, Planck-2015-A03 and Planck-2020-A2). Moreover, in two different and very peculiar situations, LFI was shut down and restarted, giving inconsistencies in data sampling. None of these data are used for scientific purposes, but to avoid discrepancies in data analysis all of the radiometers at the same frequency must have the same number of samples.

To ensure this, we compare the length of the data stream to be reduced in a specific pointing period to the data stored in the sample information object. If the length is not the same, the OBT vector is filled with missing sample times, the data vector is filled with zeros, and in the flag column the bit for "gap" is entered.

Gain modulation factor

The pseudo-correlation design of the LFI radiometers allows for a dramatic reduction of 1/f noise when the V_sky and V_load outputs are differenced (see LFI instrument description). The two streams are slightly unbalanced, since one looks at the 2.7-K sky and the other looks at the 4.5-K reference load. To force the mean of the difference to zero, the load signal is multiplied by the gain modulation factor (R). For each pointing period this factor is computed using (see equation (3) in LFI description)

[math] R = { \left\langle V_{\rm sky}\right\rangle \over \left\langle V_{\rm load}\right\rangle} [/math].

Then the data are differenced using

[math] {\rm TOI}_{\rm diff}^i = V_{\rm sky}^i – R V_{\rm load}^i [/math].

This value for R minimizes both the 1/f noise and the white noise in the difference timestream. The i index represents the diode and can be 0 or 1.

At this point, we also set the manoeuvre flag bit to identify those samples that have missing data, using the information stored in the sampling information object. This identifies which data to ignore in the next step of the Pipeline.

The R values are stored in the database. At the same time the mean values of V_sky and V_load are stored, so they can be used in other steps of the analysis.

Diode combination

The two complementary diodes of each radiometer are combined. The relative weights of the diodes in the combination are chosen for optimal noise. We assign relative weights to the uncalibrated diode streams based on their first-order calibrated noise.

Evaluation

From first-order calibration we compute an absolute gain G₀ and G₁, subtract an estimated sky signal and calculate the calibrated white noise σ₀ and σ₁, for the pair of diodes (see equation 6 in LFI description). The weights for the two diodes (i = 0 or 1) are

[math] W_i = {\sigma_i^2 \over G_{01}} {1 \over {\sigma_0^2 + \sigma_1^2}} [/math],

where the weighted calibration constant is given by

[math] G_{01} = {1 \over {\sigma_0^2 + \sigma_1^2}} \left(G_0 \sigma_1^2 + G_1 \sigma_0^2\right) [/math].

The weights are fixed to a single value per diode for the entire data set. Small variations in the relative noise of the diodes would in principle require that we recalculate the weights on shorter timescales; however, we decided that a time-varying weight could possibly induce more significant (and hard to model) systematics, so we chose a single best estimate for the weights for each diode pair.

Weights used in combining diodes.

Application

The weights in the table above are used in the formula

[math] {\rm TOI}_{\rm diff} = w_0 {\rm TOI}_{\rm diff,0} + w_1 {\rm TOI}_{\rm diff,1} [/math].

Planet flagging

Extraction method

Measurements of planets have been formed from samples containing flux from the planet, plus a surrounding region, projected onto a grid (microstripes), by assuming an elliptical Gaussian beam using parameters from instrument database.

Microstripes are a way to extract and store relevant samples for planet detection. Here relevant samples are those affected by the planet plus samples in the neighbourhood (to establish a background level). The search radius for selecting samples as relevant is 5° around the planet's position, computed at the pointing period mid-time. For each sample we store SCET (Spacecraft Event Time), pointing directions, and calibrated temperature. Destriping is applied during the application of this procedure.

Random errors are estimated by taking the variance of samples entering each micromap pixel. This method is fast but not exact, since the variance is larger near a bright source. This can cause the noise to be overestimated by a factor of 2; however, given the large S/N for planetary observations, that is not a major drawback.

The apparent position of a planet as seen from Planck at a given time is derived from JPL Horizons. Positions are tabulated in steps of 15 minutes and then linearly interpolated at the sampling frequency of each detector. JPL Horizons tables allow us also to derive other quantities such as the planet-Planck distance and the planet-Sun distance, as well as the planet angular diameter, which affects the apparent brightness of the planet.

The antenna temperature is a function of the dilution factor, according to

[math] T_{\rm ant,obs} = 4 \log 2\,T_{\rm ant,1} \left( {\theta \over b_{\rm FWHM} } \right) ^2 [/math],

where T_ant,obs and T_ant,1 are the observed and reduced T_ant, θ is the instantaneous angular diameter of the planet, and b_FWHM the beam full-width at half-maximum.

With the above definition T_ant,1 could be considered as the T_ant for a planet with b_FWHM = θ, but a more convenient view is to take a reference dilution factor D₀, as the dilution factor for a standardized angular diameter for the planet and fiducial FWHM beam b_FWHM, θ₀, to have

[math] D_0 = \left( {\theta_0 \over b_0 } \right) ^2 [/math],

leading to the following definition of a standardized T_ant:

[math] T_{\rm ant,obs} = 4 \log 2\, T_{\rm ant,0} \left( {b_{\rm FWHM,0} \over b_{\rm FWHM}} {\theta \over \theta_0} \right) ^2 [/math].

This has the advantage of removing variations among different detectors and transits, while keeping the value of T_ant similar to that seen by the instrument and then allowing a prompt comparison of signals and sensitivities.

Application

The OBT vectors found by the searches are saved in a set of objects, one for each horn. In the Level 2 pipeline those OBTs are compared with the OBT vector of the data to set the planet bit flag where needed.

Photometric calibration

Photometric calibration is the procedure used to convert data from volts to kelvins. The source of the calibration is the well understood CMB dipole, caused by the motion of the Solar System with respect to the CMB reference frame. To this signal we add the modulation induced by the orbital motion of Planck around the Sun. The resulting signal is then convoluted with the horn beam to obtain the observed dipole. For details refer to Planck-2015-A06 and Planck-2020-A2.

In the 2018 release we decided to include the sky signal in the calibration process, on the same footing as the orbital and Solar dipole, including both temperature and polarization fluctuations. Unfortunately, this is non-trivial, since the purpose of the experiment, in this case, is precisely to measure the polarized emission from the sky. A good approximation, however, can be estalished through an iterative process that alternates between gain calibration, map making and astrophysical component separation:

1. Let T(sky) be the full best-fit Planck2015 astrophysical sky model, including CMB, synchrotron, free-free, thermal and spinning dust and CO emission for temperature maps, and CMB, synchrotron and thermal dust in polarization.
2. Estimate G explicitly including the temperature and polarization component of T(sky) in the calibrator on the same footing as teh orbital and Solar Dipole.
3. Compute frequency maps with these new gains.
4. Estimate new astrophysical model from updated frequency maps using Commander. (At the moment the sky model is adjusted only for LFI frequencies.)
5. Iterate (2)--(4).

Since the true sky signal is stationary on the sky, while the spurious gain fluctuations are not, this process will in principle converge, essentially corresponding to a generalized map-maker in which the G is estimated jointly with the sky maps (see Planck-2020-A2 for further details).

Beam-convolved dipole

In computing the beam-convolved dipole we used an elegant algorithm to save time and computing power. In computing the cosmological dipole signal it is common to assume a pencil-like beam acting as a Dirac delta function. In this case a dipole timeline is defined as

[math] \Delta T_{D,\delta}(t) = \mathbf{P}_{\rm E}(t) \cdot \mathbf{D}_{\rm E} [/math]

where P_E(t) is the pointing direction in the observer reference frame and D_E(t) is the dipole axis scaled by the dipole amplitude, again in the same reference frame (here the label "E" is for "Ecliptic").

In general the true signal would have to be convolved with the beam pattern of the given radiometer, usually described as a fixed map in the beam reference frame or as a time-dependent map in the observer reference frame. In this case it is easiest to describe the convolution in the beam reference frame, since the function to be convolved then can be described by a single vector.

Denoting by [math] {\sf U}(t) [/math] the matrix converting from the observer to the beam reference frame, so that

[math] {\sf U}(t) \mathbf{P}_{\rm E}(t) = \mathbf{e}_z [/math],

the instantaneous dipole direction in the beam reference frame is

[math] \mathbf{D}(t) = {\sf U}(t) \mathbf{D}_{\rm E} [/math].

By denoting with [math] \mathbf{P} [/math] a pointing direction in the beam reference frame, then

[math] \Delta T_D(t) = N \int_{4\pi} B(\mathbf{P})\,\mathbf{P} \cdot \mathbf{D}(t)\, d^3\mathbf{P} [/math],

where N is a normalization constant defined through

[math] N^{-1} = \int_{4\pi} B(\mathbf{P}) d^3\mathbf{P} [/math].

Denoting with P_x, P_y, and P_z the three Cartesian components of P, the integral of the dot product can be decomposed into three independent integrals:

[math] S_x = N \int_{4\pi} B(\mathbf{P}) P_x d^3\mathbf{P} [/math];

[math] S_y = N \int_{4\pi} B(\mathbf{P}) P_y d^3\mathbf{P} [/math];

[math] S_z = N \int_{4\pi} B(\mathbf{P}) P_z d^3\mathbf{P} [/math].

These integrals define a time independent vector characteristic of each radiometer and constant over the mission.

Detector ID	[math] S_x [/math]	[math] S_y [/math]	[math] S_z [/math]
LFI18S	4.64653×10-3	-1.32712×10-3	9.95771×10-1
LFI18M	2.84449×10-3	-8.95117×10-4	9.97353×10-1
LFI19S	4.29488×10-3	-1.40378×10-3	9.96128×10-1
LFI19M	4.50970×10-3	-1.62551×10-3	9.95733×10-1
LFI20S	5.27978×10-3	-1.94793×10-3	9.95146×10-1
LFI20M	4.74206×10-3	-1.84621×10-3	9.95483×10-1
LFI21S	5.23772×10-3	1.93375×10-3	9.95176×10-1
LFI21M	4.37131×10-3	1.70755×10-3	9.95851×10-1
LFI22S	3.62730×10-3	1.20309×10-3	9.96790×10-1
LFI22M	3.18177×10-3	1.13834×10-3	9.97055×10-1
LFI23S	3.25825×10-3	9.10802×10-4	9.97061×10-1
LFI23M	2.63850×10-3	8.05452×10-4	9.97552×10-1
LFI24S	1.20077×10-3	-2.98774×10-7	9.98979×10-1
LFI24M	1.19670×10-3	-1.35903×10-6	9.98945×10-1
LFI25S	-2.10060×10-4	4.42870×10-4	9.99657×10-1
LFI25M	-2.51334×10-4	5.58031×10-4	9.99546×10-1
LFI26S	-1.97667×10-4	-4.22022×10-4	9.99670×10-1
LFI26M	-2.54267×10-4	-5.74267×10-4	9.99521×10-1
LFI27S	5.85555×10-3	1.81753×10-3	9.94483×10-1
LFI27M	4.99628×10-3	1.57663×10-3	9.95292×10-1
LFI28S	6.37507×10-3	-1.96172×10-3	9.93966×10-1
LFI28M	4.78777×10-3	-1.54429×10-3	9.95517×10-1

Characteristic vectors for each LFI detector.

By using this characteristic vector the calculation of the convolved dipole is simply defined by a dot product of the vector [math] \mathbf{S} [/math] and the dipole axis rotated in the beam reference frame:

[math] \Delta T (t) = \mathbf{S}^{\rm T} {\sf U}(t) \mathbf{D}_{\rm E} [/math].

Binning

In order to simplify the computation and to reduce the amount of data used in the calibration procedure, the data are phase binned into maps with N_side=256. During phase binning all the data are neglected that are flagged for manoeuvres, planets, and gaps, as well as those flagged in Level 1 analysis as not recoverable.

Fit

The first-order calibration values are given by a least squares fit between the signal and the dipole. For each pointing gain g_k and offset b_k values are computed by minimizing

[math] \chi^2 = \sum_{i \in k} {\left\{ \Delta V (t_i) - \Delta V_{\rm model} (t_i|g_k, b_k)\right\}^2 \over {\rm rms}_i^2 } [/math],

where the sum includes only samples outside a Galactic mask.

DaCapo

The largest source of error in the fit arises from unmodelled sky signal ΔT_a from CMB anisotropy. The procedure adopted to correct this effect (DaCapo) is described below.

The uncalibrated TOI y_i belonging to a pointing period k is modelled as

[math]y_{i}=g_{k}*(s_{i}+d_{i})+b_{k}+n[/math],

where the unknowns s_i, g_k, and b_k are, respectively, the signal per OBT, the gain per PID, and the offset per PID, and where d_i is the total dipole.

This is a nonlinear χ² minimization problem. It can be linearized using an iterative procedure: for each iteration step a linearized model TOI is built as

[math]y_{i,model}=g_{k}(-1)*\left\{s_{i}-s_{i}(-1)\right\}+g_{k}*\left\{d_{i}+a_{i}(-1)\right\}+b_{k}[/math],

where g_k(-1) and s_i(-1) are the gain and sky signal computed at the previous iteration step.

A linear fit is performed between y_i and y_i,model to obtain the new g_k and s_i values. The procedure is iterated until convergence. To reduce the impact of the noise during the iterative procedure the sky estimation is built using data from both radiometers of the same horn.

Smoothing

To improve accuracy given by the iterative algorithm and remove noise from the solution a smoothing algorithm must be applied.

OSGTV

OSGTV is a 3-step smoothing algorithm, implemented with a C++ code.

The gain reconstructed with DaCapo can be expressed as

[math]G_{\rm raw}(t,T(t))=G_{\rm true}(t,T(t))+G_{\rm noise}(t)[/math],

where the T(t) function represents temperature fluctuations of the Focal Plane. The time dependence of the "real" gain G_true is modelled as the superposition of a "slow" component, with a timescale of about 3 months, and a "fast" component with a timescale of a few PIDs:

[math]G_{\rm true}=G_{\rm slow}+G_{\rm fast}[/math].

The slow component takes into account the seasonal variations of the thermal structure of the spacecraft due to the orbital motion, while the "fast" component describes the thermal effects of the electronics and compressors, as well as single events like the sorption cooler switchover.

To disentangle the components of G_true, we apply a parametric "hybrid" approach in three steps.

Step 1. For each PID i, we used the 4-K total-power V_load(i) and the signal from temperature detectors in the focal plane T_i, subsampled at 1 sample/PID, to track gain changes. This is implemented through a linear fit between V_load(i) × G_raw and T_i:

[math]V_{\rm load}(i)\times G_{\rm raw}=K_{0}+K_{1} \times (T_{i}-\langle T_{\rm MW}\rangle)[/math],

where the window length MW of the moving average is proportional to the variance of the dipole in the PID being considered. The resulting gain is

[math] G_{i} = \frac{ K_{0} + K_{1} \times (T_{i} - \langle T_{\rm MW} \rangle ) }{ V_{\rm load}(i) } [/math].

Step 2. The "fast" component G_fast is recovered as follows: we define a maximum moving average window length WL_max,and for each PID we compute the variance σ²_i of G_i in this window. We define a percentile on the ordered variance array and we compute the corresponding value of the variance σ²_p. The window length for each PID is then computed as

[math]{\rm WL}_{i}=\frac{\sigma_{\rm p}^2 \times {\rm WL}_{\rm max}}{\sigma_{i}^2}[/math].

If WL_i > WL_max we impose WL_i = WL_max. With these window lengths a moving window average is performed on G_i. The averaged gain vector is subtracted from the raw hybrid gain to obtain G_fast.

Step 3. We perform a moving window average on G_i and we compute the variances of the smoothed array. The window length is computed with a linear interpolation between a minimum length WL_min defined in the dipole minima and a maximum WL_max defined in the dipole maxima. The array of gain variances is weighted with the variance of the dipole. We set a percentile on the variance array and we find the corresponding variance value σ²_p. Around this value we search for local maxima of the variance array, and we split the domain of the gain into subsets between consecutive maxima. For each subset we perform a moving average with the corresponding window length. The "slow" component G_slow is given by the union of these subsets.

Gain application

The last step in TOI processing is the creation of the calibrated stream. For each sample we have

[math] {\rm TOI}_{\rm cal}(t) = ({\rm TOI}_{\rm diff}(t) – {\rm offset}(k)) \, g(k) \, - \, {\rm convDip}(t)\, - \, T_{\rm stray}(t)[/math],

where t is the time and k is the pointing period, "convDip" is the CMB dipole convolved with the beam, and T_stray is the stray light.

Noise

The aim of this pipeline step is the reconstruction of the noise parameters from calibrated flight TOI. The goal is two-fold. On the one hand we need to know the actual noise properties of our instrument in order to properly take them into account, especially during later processing and analysis steps, such as map-making and power spectrum estimation. On the other hand, evaluation of noise properties during the instrument lifetime is a way to track down possible variations, anomalies, and general deviations from the expected behaviour.

Operations

Noise estimation is performed on calibrated data; since we would like to track possible noise variations through the mission lifetime, we select data in chunks of five ODs (Operational Days). These data are processed by the ROMA iterative generalized least-squares (IGLS) mapmaking algorithm, which includes a noise estimation tool. In general IGLS mapmaking is a quite costly in terms of time and resources required. However, the length of the data is such that it can run on the DPC cluster in a very short time (around 1-2 minutes).

The method implemented can be summerized as follows. We model the calibrated TOI as

[math] \mathbf{\Delta T} = {\sf P} \mathbf{m} + \mathbf{n} [/math],

where n is the noise vector and P is the pointing matrix that links a pixel in the map m with a sample in the TOI d. The initial estimation of the signal is obtained by simply rebinning the TOI into a map. Then an iterative approach follows in which both signal and noise are estimated according to

[math] \mathbf{\hat{n}}_i = \mathbf{\Delta T} - {\sf P}\mathbf{\hat{m}}_i [/math]

[math] \mathbf{\hat{m}}_{i+1} = \left({\sf P}^{\rm T}\hat{\sf N}_i^{-1}{\sf P}\right)^{-1}{\sf P}^{\rm T}\hat{\sf N}_i^{-1}\Delta T [/math],

where N_i is the noise covariance matrix in the time domain resulting from iteration i. We find that convergence is achieved after three iterations.

We then perform an FFT (Fast Fourier Transform) on the noise timestream output from from the iterative approach, and fit the resulting spectrum.

Fitting pipeline

As already done in the 2013 and 2015 release, we estimate the parameters of the noise properties (i.e., white noise level, knee-frequency, and slope of the low-frequency noise component) by means of an MCMC approach. Therefore for the spectra just described we first compute the white noise level by taking the mean of the last 10% of the data (at 30 GHz due to the higher value of the knee-frequency this quantity is reduced to 5%). Once the white noise level has been determined we proceed with the actual fitting of the knee-frequency and slope. The resulting values reported are the medians of the fitted values for our 5-OD chunks, through the whole mission lifetime.

Horn	White noise M [[math]\mu[/math]K s[math]^{1/2}[/math]]	White noise S [[math]\mu[/math]K s[math]^{1/2}[/math]]	Knee-frequency M [mHz]	Knee-frequency S [mHz]	Slope M	Slope S
18	512.5±2.0	466.7±2.3	14.8±2.1	17.8±1.5	-1.06±0.08	-1.18±0.10
19	578.9±2.1	554.2±2.2	11.7±1.1	13.7±1.3	-1.21±0.23	-1.10±0.13
20	586.9±1.9	620.0±2.7	7.9±1.5	5.6±1.0	-1.19±0.27	-1.30±0.33
21	450.4±1.4	559.8±1.8	37.9±5.7	13.1±1.3	-1.24±0.08	-1.20±0.08
22	490.1±1.3	530.9±2.2	9.5±1.7	14.3±6.7	-1.41±0.25	-1.23±0.27
23	503.9±1.6	539.1±1.7	29.6±1.1	58.9±1.6	-1.07±0.02	-1.21±0.02
24	462.8±1.3	400.5±1.1	26.9±1.0	89.6±13.8	-0.94±0.01	-0.91±0.01
25	415.2±1.3	395.0±3.1	19.7±1.0	46.8±1.9	-0.85±0.01	-0.90±0.01
26	482.6±1.9	422.9±2.5	64.4±1.8	70.7±18.7	-0.92±0.01	-0.75±0.07
27	281.5±2.0	302.8±1.8	173.7±3.1	109.6±2.5	-0.93±0.01	-0.91±0.01
28	317.9±2.4	286.1±2.1	128.5±10.9	44.1±2.2	-0.93±0.01	-0.90±0.02

Time variations of noise parameters are a good tracer of possible modifications in the instrument behaviour and we know that some events capable of affecting instrument behaviour happened during the mission. Variations of the physical temperature of the instrument due to the transition in the operations from the first sorption cooler to the second one, as well as the observed degradation in the performances of the first cooler, are events that clearly show their imprints in the variation of the noise spectra.

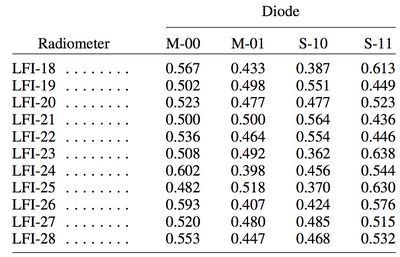
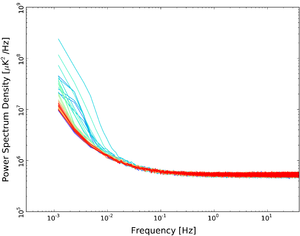
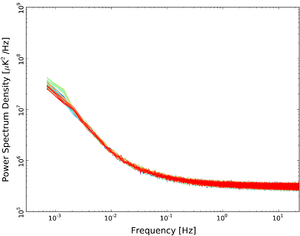
In the following figure we report a representative sample of noise spectra, one for each frequency channel (from left to right LFI 18M, LFI 25S, and LFI 27M), covering the whole mission lifetime. The white noise is extremely stable at the level of 0.1%. As already noted in the 2013 and 2015 release, knee-frequencies and slopes are stable until OD 326 and show clear variations and deviations from the simple one knee-frequency and one slope model. This is a sign of the degradation of the first cooler inducing thermal variations, with a characteristic knee-frequency (different from the radiometric one) and with a steeper slope. Once the second cooler became operational and performed as expected, the noise spectra gradually returned to the original shape at the beginning of the mission. This behaviour is visible, although not identical, at each frequency for several reasons e.g., intrinsic thermal susceptibility and position on the focal plane that determines the actual thermal transfer function.

Noise power spectra for selected LFI radiometers.