Astrophysical component separation
Contents
[hide]CMB and foreground separation[edit]
The component-separation papers, Planck-2013-XII[1], Planck-2015-A09[2] and Planck-2020-A4[3] (and references therein), give details of these processing steps. Four separate component-separation methods are used, which we now describe in turn.
Commander[edit]
The Commander approach implements Bayesian component separation, fitting a parametric model to the data by sampling the corresponding posterior distribution. The computational engine in this approach is standard Gibbs sampling. The general Commander model includes both cosmological parameters (i.e., the CMB map and power spectrum), astrophysical parameters (e.g., synchrotron, free-free, spinning and thermal dust, and CO emission), and instrumental parameters (e.g., calibration factors, absolute zero-levels, and bandpass corrections). The full model was employed in the Planck 2015 analysis (Planck-2015-A10[4]) which included both single-detector Planck maps and external observations from WMAP and Haslam. For the reduction of the Planck 2018 data set, which includes only full-frequency maps, a simpler model is employed, in which only a single joint power-law low-frequency foreground model is included in the fit, accouting simultaneously for synchrotron, free-free and spinning dust emission, and no bandpass corrections are applied. (Note that 'bandpass corrections' in this setting implies fitting for the actual bandpass profile of each detector, and not standard colour correction and unit conversion, which always is performed in all cases.) For polarization analysis, the signal model includes only CMB, synchrotron and thermal dust emission.
A major difference between the Planck 2015 and 2018 Commander analyses is the introduction of Commander2 in 2018. As discussed by Eriksen et al. 2008[5] and Planck-2015-A10[4], the first version of the Commander code required all frequency maps to have identical angular resolution. In practice, this required smoothing of all maps to 1 degree FWHM if external data sets (WMAP and Haslam 408 MHz) were considered, or 40 arcmin FWHM for Planck alone. Higher resolution could only be achieved by omitting lower frequencies from the fit. Either approach translates into non-optimal use of the available information content. This restriction is removed by the Commander2 implementation (see Seljebotn et al. 2018), which accounts explicitly for the specific instrumental beam of each frequency channel. Furthermore, by processing the data at full angular resolution Commander2 additionally supports fitting of individual point sources, given some beam template for each object. The 2018 Commander processing employs FEBeCoP templates centered on the closest pixel for this purpose.
NILC[edit]
NILC is a linear method for combining the input frequency channels. It implements an "internal linear combination" method with weighting coefficients varying over the sky and over the multipole range up to ℓ=3200, and it does so using "needlets," which are spherical wavelets. A special procedure is used for processing the coarsest needlet scale, which contains the large-scale multipoles.
In practice, our NILC processing depends on several implementation choices, as follows.
- Input channels
- In this implementation, the NILC algorithm is applied to all Planck channels from 44 to 857 GHz, omitting only the 30-GHz channel.
- Pre-processing of point sources
- Identical to the SMICA pre-processing.
- Masking and inpainting
- The NILC CMB map is actually produced in a three-step process. In a first step, the NILC weights are computed from covariance matrices evaluated using a Galactic mask removing about 2 % of the sky (and apodized at °). In a second step, those NILC weights are applied to needlet coefficients computed over the complete sky (except for point source masking/subtraction), yielding a NILC CMB estimate over the full sky (except for the point source mask). In other words, the weights are computed over a masked sky, but are applied to a full sky (excluding point sources). In a final step, the pixels masked due to point source processing are replaced by the values of a constrained Gaussian realization ("inpainting").
- Spatial localization
- The boundaries of the zones used for spatial localization are obtained as iso-level curves of a low resolution map of Galactic emission.
- Beam control and transfer function
- As in the SMICA processing, the input maps are internally re-smoothed to a 5 arcmin resolution, so the resulting CMB map is automatically synthesized with an effective Gaussian beam of 5 arcmin, according to the unbiased nature of the ILC.
- Using SMICA recalibration
- In our current implementation, the NILC solution uses the values determined by SMICA for the CMB spectrum.
SEVEM[edit]
SEVEM produces cleaned CMB maps at individual frequencies by using a procedure based on template fitting, which can then be combined to produce a final CMB map. The templates are internal, i.e., they are constructed from Planck data, avoiding the need for external data sets, which usually complicates the analyses and may introduce inconsistencies. The method has been successfully applied to Planck simulations (Leach et al., 2008[6]), to WMAP polarization data (Fernandez-Cobos et al., 2012[7]) and to the previous Planck data releases (Planck-2013-XII[1], Planck-2015-A09[2]). In the cleaning process, no assumptions about the foregrounds or noise levels are needed, rendering the technique very robust.
Regarding intensity, the pipeline for the 2018 release does not present any significant change with respect to the previous one, although we provide now a cleaned 70 GHz map in intensity. However, for polarization, given the significant improvement in the quality of the data, we are now able to clean robustly also the 217 GHz map which can be included in the final combined map and, therefore, construct a CMB map with better resolution and higher signal-to-noise. Thus, conversely to the 2015 release, the SEVEM polarization maps are now provided at full resolution (Nside=2048, with a resolution equivalent to that of a Gaussian beam of 5 arcminutes).
The input maps used are all the Planck frequency channels. In the current release, we have cleaned the 70, 100, 143, and 217 GHz maps for both intensity and polarization, at their native resolution. For intensity, we use the same four templates to clean the 100, 143 and 217 GHz. Three of them are constructed as the difference of the following Planck channels (smoothed to a common resolution to remove the CMB contribution): [30GHz – 44GHz], [44GHz – 70GHz], and [545GHz – 353GHz], whereas the fourth template is given by the 857-GHz channel (smoothed with the beam of the 545-GHz channel). In addition, we also clean the 70 GHz map using two templates, the [30GHz – 44GHz] difference map and a second template given as the difference [353GHz – 143GHz] constructed at the resolution of the 70 GHz map. For polarization, given the smaller number of frequency channels available, a different set of templates has to be chosen for each map. In particular, two templates are used to clean 70 GHz and three templates are considered for the rest of the frequencies (see Appendix C in Planck-2020-A4[3] for details). Before constructing the templates, for both intensity and polarization, we inpaint the positions of point sources detected in the frequency maps, to reduce contamination in the final map.
A linear combination of the templates is then subtracted from the Planck sky map at the considered frequency, in order to produce the cleaned CMB map. The coefficients of the linear combination are obtained by minimizing the variance of the cleaned map outside a given mask. Although we exclude very contaminated regions during the minimization, the subtraction is performed for all pixels and therefore the cleaned maps cover the full-sky (although, of course, foreground residuals are expected to be particularly large in the areas excluded in the minimisation). Inpainting of point sources is also carried out in the cleaned maps.
The final CMB intensity map has then been constructed by combining the 143 and 217 GHz cleaned maps by weighting them in harmonic space taking into account the noise level, the resolution and a rough estimation of the foreground residuals of each map (obtained from realistic simulations). This final map has a resolution corresponding to a Gaussian beam of FWHM=5 arcmin at Nside=2048. The final CMB polarization map has been obtained by combining the 100, 143 and 217 GHz cleaned maps taking into account the noise and resolution of each channel and suppressing the largest scales of the 217 GHz map, which are expected to be more affected by residual systematics. The Q/U maps have been constructed at Nside=2048 and have a resolution of 5 arcmin.
SMICA[edit]
SMICA reconstructs a CMB map as a linear combination in the harmonic domain of Nchan input frequency maps with weights that depend on multipole ℓ. Given the Nchan× 1 vector xℓm of spherical harmonic coefficients for the input maps, it computes coefficients sℓm for the CMB map as
where the Nchan× 1 vector wℓ , which contains the multipole-dependent weights, is built to give unit gain to the CMB with minimum variance. This is achieved with
where vector a is the emission spectrum of the CMB evaluated at each channel (allowing for possible inter-channel recalibration factors) and Rℓ is the Nchan × Nchan spectral covariance matrix of xℓm. Taking Rℓ in the second equation to be the sample spectral covariance matrix Řℓ of the observations:
would implement a simple harmonic-domain ILC. However, this is not what SMICA does. As discussed below, we instead use a model Rℓ (θ) and determine the covariance matrix to be used in the second equation by fitting Rℓ(θ) to Řℓ. This is done in the maximum likelihood sense for stationary Gaussian fields, yielding the best fit model parameters θ as
SMICA models the data as a superposition of CMB, noise, and
foregrounds. The latter are not parametrically modelled; instead, we
represent the total foreground emission by d templates
with arbitrary frequency spectra, angular spectra and correlations, i.e.,
where Cℓ is the angular power spectrum of the CMB, A is a Nchan × d matrix, Pℓ is a positive d × d matrix, and Nℓ is a diagonal matrix representing the noise power spectrum. The parameter vector θ contains all or part of the quantities in the above equation.
The above equations summarize the basic principles of SMICA; its actual operation depends on a choice for the spectral model and on several execution-specific details.
The actual implementation of SMICA includes the following steps:
- Inputs
- All nine Planck frequency channels from 30 to 857 GHz, harmonically transformed up to ℓ = 4000.
- Fit
- In practice, the SMICA fit (i.e., the minimization of the fourth equation above), is conducted in three successive steps. We first estimate the CMB spectrum by fitting all model parameters over a clean fraction of sky in the range 100 ≤ ℓ ≤ 680 and retaining the best fit value for vector a. In the second step, we estimate the foreground emissivity by fixing a to its value from the previous step and fitting all the other parameters over a large fraction of sky in the range 4 ≤ ℓ ≤ 150 and retaining the best fit values for the matrix A. In the last step, we fit all power spectrum parameters; that is, we fix a and A to their previously found values and fit for Cℓ and Pℓ at each ℓ.
- Beams
- The discussion thus far has assumed that all input maps have the same resolution and effective beam. Since the observed maps actually vary in resolution, we process the input maps in the following way. To the ith input map with effective beam bi(ℓ) and sampled on a HEALPix grid with Niside, the CMB sky multipole sℓm actually contributes sℓmaibi(ℓ) pi(ℓ), where pi(ℓ) is the pixel window function for the grid at Niside. Seeking a final CMB map at 5-arcmin resolution, the highest resolution of Planck, we work with input spherical harmonics re-smoothed to 5 arcmins, ~xℓ; that is, SMICA operates on vectors with entries ~xiℓm = xiℓmb5(ℓ) / bi(ℓ) / pi(ℓ), where b5(ℓ) is a 5 arcmin Gaussian beam function. By construction, SMICA then produces a CMB map with an effective Gaussian beam of 5 arcmin (without the pixel window function).
- Pre-processing
- We start by fitting point sources with S/N > 5 in the PCCS catalogue in each input map. If the fit is successful, the fitted point source is removed from the map; otherwise it is masked and the hole inpainted. This is done at all frequencies except 545 and 857 GHz, where all point sources with S/N > 7.5 are masked and inpainted.
- Masking and inpainting
- In practice, SMICA uses a small Galactic mask, leaving 97% of the sky. However, we deliver a full-sky CMB map in which the masked pixels (Galactic emission and point sources) are replaced by a constrained Gaussian realization.
- Binning
- In our implementation, we use binned spectra.
- High ℓ
- Since there is little point trying to model the spectral covariance at high multipoles (because the sample estimate is sufficient), SMICA implements a simple harmonic ILC at ℓ > 1500; i.e., it applies the filter (second equation above) with Rℓ = Řℓ.
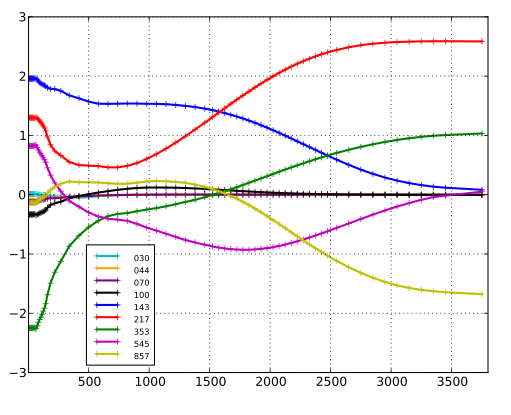
Viewed as a filter, SMICA can be summarized by the weights wℓ applied to each input map as a function of multipole. In this sense, SMICA is strictly equivalent to co-adding the input maps after convolution by specific axisymmetric kernels directly related to the corresponding entry of wℓ. The SMICA weights used here are shown below for input maps in units of K. They show, in particular, the (expected) progressive attenuation of the lowest resolution channels with increasing multipole.
References[edit]
- ↑ Jump up to: 1.01.1 Planck 2013 results. XI. Component separation, Planck Collaboration, 2014, A&A, 571, A11.
- ↑ Jump up to: 2.02.1 Planck 2015 results. XI. Diffuse component separation: CMB maps, Planck Collaboration, 2016, A&A, 594, A9.
- ↑ Jump up to: 3.03.1 Planck 2018 results. IV. Diffuse component separation, Planck Collaboration, 2020, A&A, 641, A4.
- ↑ Jump up to: 4.04.1 Planck 2015 results. X. Diffuse component separation: Foreground maps, Planck Collaboration, 2016, A&A, 594, A10.
- Jump up ↑
- Jump up ↑ Component separation methods for the PLANCK mission, S. M. Leach, J.-F. Cardoso, C. Baccigalupi, R. B. Barreiro, M. Betoule, J. Bobin, A. Bonaldi, J. Delabrouille, G. de Zotti, C. Dickinson, H. K. Eriksen, J. González-Nuevo, F. K. Hansen, D. Herranz, M. Le Jeune, M. López-Caniego, E. Martínez-González, M. Massardi, J.-B. Melin, M.-A. Miville-Deschênes, G. Patanchon, S. Prunet, S. Ricciardi, E. Salerno, J. L. Sanz, J.-L. Starck, F. Stivoli, V. Stolyarov, R. Stompor, P. Vielva, A&A, 491, 597-615, (2008).
- Jump up ↑ Multiresolution internal template cleaning: an application to the Wilkinson Microwave Anisotropy Probe 7-yr polarization data, R. Fernández-Cobos, P. Vielva, R. B. Barreiro, E. Martínez-González, MNRAS, 420, 2162-2169, (2012).
Cosmic Microwave background
Full-Width-at-Half-Maximum
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).