Beams

Scanning Beams

The scanning beams describe the instrument’s instantaneous beam profile. Due to the near constant spin rate of the spacecraft, time domain effects (including residual time response and lowpass filtering) are degenerate with the spatial response due to the optical system. The scanning beam reconstruction recovers both of these effects, aside from residual time domain effects on a longer time scale than can be captured with the extent of the scanning beam model.

In #planck2013-p03c we consider two models of the beam in order to better understand systematics in the reconstruction. Here we describe only the B-Spline beams which are used to compute the delivered effective beam (see next section).

B-Spline Beam construction

We use seasons 1 and 2 of the Mars observation to reconstruct the beam. The data are processed with the bigPlanets TOI processing. We use JPL Horizons ephemerides to determine the pointing of each detector relative to the planet. We subtract the astrophysical background in the time domain using a bicubic interpolation of the Planck maps.

The time ordered data are used to fit a two dimensional B-Spline surface using a least square minimization and a smoothing criterion to minimize the effects of high spatial frequency variations. We therefore assume the scanning beam to be smooth. The smoothing criterion as well as the locations of the nodes used to compute the B-Spline basis functions are set using GRASP physical optics simulations as inputs which are the best assumptions on the spatial frequency content of the in-flight beams.

The smoothing criterion is defined as follows:

[math]\eta = \displaystyle{\sum_{i=1}^{g}\left(b^{k}(\lambda_{i+})-b^{k}(\lambda_{i-})\right)^2} \label{smoothcrit}[/math]

[math]\begin{aligned} \eta &: \mbox{ Smoothing Criterion}\\ b^k &: \mbox{ $k^{th}$ beam derivative evaluated on the nodes locations}\end{aligned}[/math]

And the global inversion criterion :

[math]\zeta = \eta + p\times \delta[/math]

with [math]\delta[/math] usual least square estimator and [math]p[/math] coefficient giving the relative weight to [math]\delta[/math] with respect to the smoothing criterion.

[math]\delta = \displaystyle{\sum_{r=1}^{m}}\left(y_{r} - b(x_{r})\right)^2\label{estimator}[/math]

[math]\begin{aligned} \delta &: \mbox{ usual least square criterion}\\ r &: \mbox{ indice relative to the m data points, } r \in \{1, \ldots, m\}\\ y_r &: \mbox{ planet data of sample r}\\ x_r &: \mbox{ pointing of sample r}\\ b &: \mbox{ reconstructed beam}\end{aligned}[/math]

The B-Spline nodes are located on a regular spaced grid in the detector coordinate framset. At the edge of the reconstructed beam map area, 4 coincident nodes are added to avoid vanishing basis functions.

Let [math]B_{i, k+1}[/math], [math]k[/math] degree B-Spline build using nodes {[math]\lambda_{i}, ..., \lambda_{i+k+1}[/math]} (De Boor & Cox, 1972) :

[math]B_{i,1}(x) = \left\{ \begin{array}{l} 1, \mbox{ si } x \in \mbox{[} \lambda_{i}, \lambda_{i+1} \mbox{[}\\ 0, \mbox{ si } x \notin \mbox{[} \lambda_{i}, \lambda_{i+1} \mbox{[} \end{array} \right.[/math]

[math]B_{i, l+1}(x) = \displaystyle{\frac{x - \lambda_{i}}{\lambda_{i+l} - \lambda_{i}}} B_{i,l}(x) + \displaystyle{\frac{\lambda_{i+l+1}-x}{\lambda_{i+l+1}-\lambda_{i+1}}} B_{i+1, l}(x)[/math]

[math]l=1, \ldots, k[/math]

Figure 1: Focal plane plot of B-Spline scanning beams using in-flight pointing reconstruction. The contours are -3,-10,-20,-30 dB from the peak, and for PSB pairs the "a" bolometer is plotted in black and "b" in blue.

Simulations and errors

We estimate the reconstruction bias and noise in the measurements using an ensemble of simulated planet observations for each channel. Further details are discussed in #planck2013-p03c. Kept fixed in each simulation are:

• the input beam assumed: we use a supersampled version of the reconstructed B-Spline beam (or whatever comes out of the current ongoing tests!)
• Astrophyical background is the same as that subtracted from the real data.
• StarTracker pointing (using the ptcor6 pointing model).

The following are varied in each simulation:

• detector noise realizations obtained by filtering randomly generated white noise with the measured noise PSDs
• random pointing errors with 2 arcsecond rms, and a spectrum that replicates the real errors.
• simulated glitches and the deglitching procedure
• Mars brightness temperature variability

400 simulated timelines are generated for each bolometer and for each of the two seasons of Mars observations used in the beam reconstruction. The simulated timelines are made into beam maps, projecting onto the B-Spline basis in the same way as the real data.

The beam maps are propagated to effective beam window functions using the quickbeam approach (see effective beams below) and used to evaluate the reconstruction bias and to construct error eigenmodes in the effective beam window function.

Residuals

There are two known beam effects that are not included in the main beam model and are estimated as a separate bias in flux and angular power spectrum measurement: 1. long tails due to errors in low frequency time response deconvolution, and 2. near sidelobes.

We stack all five observations of Jupiter to estimate the long time scale residuals due to incomplete deconvolution of the long time scale response.

Effect of Mirror Support Print-through (Dimpling)

The Planck reflectors suffer from print-through of the honeycomb structures that support the carbon-fibre face sheets. For more details see:

"Planck Telescope RF Performance Independent Verification Phase1",Per Heighwood Nielsen, February 2005. TICRA report S-1287-07.

"Planck Flight Radio Frequency Performances Quilting Analysis", D.Dubruel, July 2009, Thales Alenia Space, report H-P-ASP-AN-1839

"RF effect of dimpling distortion on the PLANCK telescope",Per Heighwood Nielsen,April 2004, TICRA report S-1281-01

While the size of the deformation has been measured during tests below room temperature to be less than 20 microns, it is the strict periodicity of the deformation that contributes most to the additional beam-shape contribution.

A simple grating equation has been shown to describe the angular positions of the resulting near side lobes very well:

[math]   \quad\quad\quad\quad \sin \theta _n = \frac{n \lambda}{Yd} [/math]

where [math]\theta _n [/math]is the angular position of the n'th order lobe from the central beam peak; [math]\lambda[/math] is the wavelength of the radiation; [math]d [/math]is the grating spacing of the periodicity and [math]Y [/math] is a factor that describes the position of the each reflector along the optical path.

[math]Y=1.00[/math] for the primary reflector and [math]Y=1.80[/math] for the secondary reflector.

Three possible periodicities ( 19.6mm, 30mm, 52mm) in the honeycomb array dominate the Planck dimpling pattern for the 857GHz detectors, though only those for the 52mm can be seen for the 545GHz and 353GHz detectors.

For the highest frequency detectors, only the weaker lobes due to the 19.6mm and 30mm periodicities are seen outside the 40 arcminute beam window, but they contribute at most [math](0.05\pm 0.008)[/math]percent to the integrated beam.

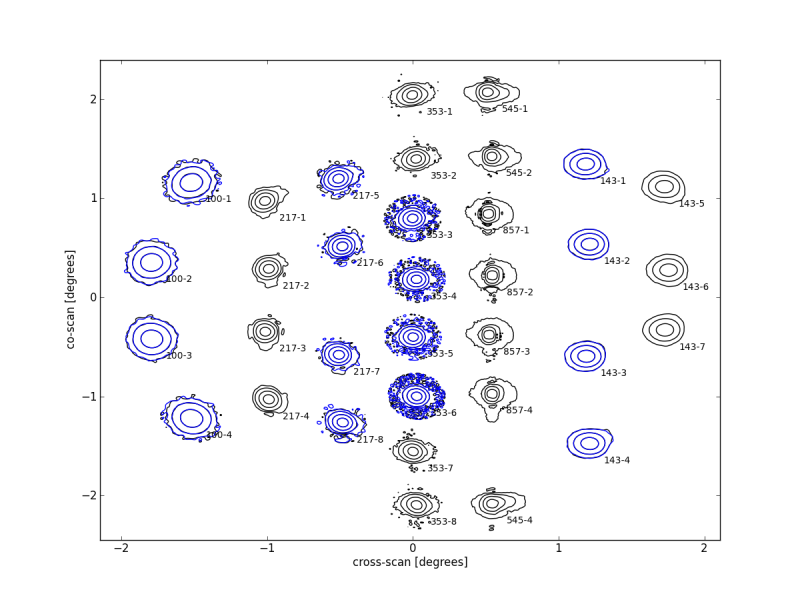
A map of Jupiter has been created for each 857GHz detector, using the first four surveys, with the background subtracted using the same sky area for the survey taken 12 months before in which the planet is not present.

The background-subtracted maps for each survey were then stacked to make a single map for each of the four detectors and these were further stacked to create a single 857GHz band map, using the standard detector weightings proportional to [math]1/(NET)^2[/math].

All the maps have 96 pixels per side, covering [math] \pm 1.4 ^\circ [/math], and are scaled to the RMS noise of the background. Central beam values range from 205,000 to 256,000, depending on the noise of the detector.

For each of these five maps of Jupiter an elliptical gaussian main beam has been fitted, and the amount of saturation estimated by finding the peak increase that gives the best gaussian fit---typically 10--20 percent.

A circular ruze envelope was also fitted together with a tilted gaussian component slightly offset from the beam in the cross-scan (optical X axis) direction, using data more than [math]0.13^\circ[/math] from the beam, with the known positions of the dimpling lobes masked out.

Once these strongest components were removed, a tilted elliptical gaussian was fitted for each visible dimpling lobe in up to 5 different sets of lobes, however the innermost lobe set (52mm periodicity) is generally obscured by the ruze component and for the outermost set (19.6mm periodicity) most lobes are too weak to be fitted for individual detectors.

The contributing areas of the lobes were determined by three methods: from the fitted gaussians; from summation within boxed areas using offsets determined from surrounding boxed areas; from summation in the boxed areas using an offset determined from gaussian fitting.

The uncertainties in the beam component areas given here include the spread in values from these different methods. Similarly, the lobe peaks in decibels are calculated using the raw, fitted and estimated desaturated beam peak values, and the uncertainties reflect the variations produced by the three methods.

Averaged over the five map fittings, the dimpling lobes contribute [math] (0.47\pm 0.13)[/math] percent of the beam area, while the ruze envelope accounts for [math] (9.2\pm 0.7)[/math] percent of the beam with the main beam making up the remaining [math](90.3 \pm 0.7)[/math] percent .

For lower frequencies the dimpling lobes are less visible and will not be discussed here. For example, the noise floor for the 545GHz band map is about 47dB below the observed Jupiter peak, so that no dimpling lobes are visible further out than the 52mm lobes at [math]0.61^\circ[/math]. For 353GHz the noise floor is at about 38dB so that even the 52mm lobes are not observed.

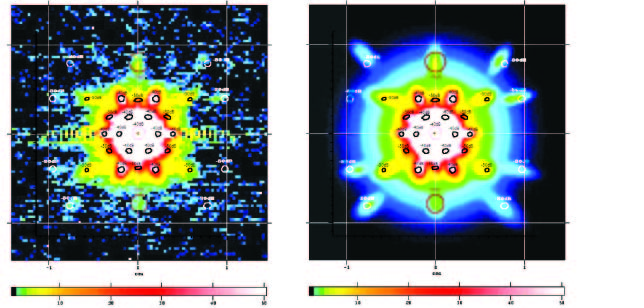
This figure shows how the dimpling lobes seen for the 857GHz band Jupiter map correspond to the contours calculated by the physical optics GRASP package, produced by TICRA, Denmark.

The GRASP simulation was performed for the 857-1 detector and assumed a uniform dimpling distortion of 10 microns.

The biggest departure from the simple grating model, is that the lobe pattern is elongated in the cross-scan (vertical) direction---lobes that should lie on a line [math]30^\circ [/math] from the vertical are consistently found around [math]25^\circ [/math] and those on the [math]60^\circ [/math] line cluster around [math]53^\circ[/math].

This is due to the offset geometry of the mirror system, whereby the dimpling print-though is foreshortened along the optical x-axis due to the tilt of the mirrors, producing greater lobe spacing as seen by the incoming photons.

The amplitudes of the fitted dimpling lobes vary significantly within each set whereas the GRASP model shows a constant amplitude for lobes within a set, except for the 30mm periodicity. Similar amplitudes are seen in lobes lying directly across the beam centre from each other, indicating that facesheet dimpling has not occurred uniformly in all directions as the GRASP model assumes.

For the 30mm periodicity the vertical lobes are significantly weaker than those at the sides just as the GRASP model also shows. Generally, the fitted lobes are somewhat stronger than those seen by GRASP, indicating that the dimpling is indeed larger than 10 microns.

While the dimpling lobes are measureable at the highest two frequencies, with a strong source (i.e. Jupiter), 90 percent of the dimpling lobe area at 857GHz, and 100 percent for all other frequencies, already appears in the beam functions described above and need no further correction. However, the presence of the uniform dimpling lobes provides a useful window by which to investigate the mirror geometry.

Effective Beams

The effective beam is the average of all scanning beams pointing at a certain direction within a given pixel of the sky map for a given scan strategy. It takes into account the coupling between azimuthal asymmetry of the beam and the uneven distribution of scanning angles across the sky. It captures the complete information about the difference between the true and observed image of the sky. They are, by definition, the objects whose convolution with the true CMB sky produce the observed sky map.

Several methods of effective beams determination have been developped and cross-validated.

The main products are produced using FEBeCoP and details of the processing are given in the Effective Beams products page. See also the equivalent page discussing the LFI beams

FEBeCoP

---

The full algebra for this method for the calculation of effective beams was presented in [Mitra, Rocha, Gorski et al.] #mitra2010. Here we summarise the main results. The observed temperature sky [math]\widetilde{\mathbf{T}} [/math] is a convolution of the true sky [math]\mathbf{T} [/math] and the effective beam [math]\mathbf{B}[/math]:

[math] \widetilde{\mathbf{T}} \ = \ \Delta\Omega \, \mathbf{B} \cdot \mathbf{T}, \label{eq:a0} [/math]

where

[math] B_{ij} \ = \ \left( \sum_t A_{ti} \, b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) \right) / \left({\sum_t A_{ti}} \right) \, , \label{eq:EBT2} [/math]

[math]t[/math] is time samples, [math]A_{ti}[/math] is [math]1[/math] if the pointing direction falls in pixel number [math]i[/math], else it is [math]0[/math], [math]\mathbf{p}_t[/math] represents the exact pointing direction (not approximated by the pixel centre location), and [math]\hat{\mathbf{r}}_j[/math] is the centre of the pixel number [math]j[/math], where the scanbeam [math]b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t)[/math] is being evaluated (if the pointing direction falls within the cut-off radius of [math]\sim 2.5 \times[/math] FWHM.

The algebra is a bit more involved for polarised detectors. The observed stokes parameters at a pixel [math]i[/math], [math](\widetilde{I}, \widetilde{Q}, \widetilde{U})_i[/math], are related to the true stokes parameters [math](I, Q, U)_i[/math], by the following relation:

[math] ( \widetilde{I} \quad \widetilde{Q} \quad \widetilde{U})_i^T \ = \ \Delta\Omega \sum_j \mathbf{B}_{ij} \cdot (I \quad Q \quad U)_j^T, \label{eq:a1} [/math]

where the polarised effective beam matrix

[math] \mathbf{B}_{ij} \ = \ \left[ \sum_t A_{tp} \mathbf{w}_t \mathbf{w}^T_t \right]^{-1} \sum_t A_{ti} \, b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) \, \mathbf{w}_t \mathbf{W}^T(\hat{\mathbf{n}}_j,\hat{\mathbf{p}}_t) \, , \label{eq:a2} [/math]

and [math]\mathbf{w}_t [/math]and [math]\mathbf{W}(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) [/math] are the the polarisation weight vectors, as defined in \cite{mitra2010}.

The task is to compute [math]B_{ij}[/math] for temperature only beams and the [math]3 \times 3[/math] matrices [math]\mathbf{B}_{ij}[/math] for each pixel [math]i[/math], at every neighbouring pixel [math]j[/math] that fall within the cut-off radius around the the center of the [math]i^\text{th}[/math] pixel.

The effective beam is computed by stacking within a small field around each pixel of the HEALPix sky map. Due to the particular features of Planck scanning strategy coupled to the beam asymmetries in the focal plane, and data processing of the bolometer and radiometer TOIs, the resulting Planck effective beams vary over the sky.

FEBeCoP, given information on Planck scanning beams and detector pointing during a mission period of interest, provides the pixelized stamps of both the Effective Beam, EB, and the Point Spread Function, PSF, at all positions of the HEALPix-formatted map pixel centres.

FICSBell

For more details, see #planck2013-p03c.

Since the HFI beams are not azimuthally symmetric, the scanning strategy has to be taken into account in the effective beam response modelling. This is done using the FICSBell method (Hivon et al, in preparation), which generalizes to polarization and to include other sources of systematics the approach used for TT [math]C(l)[/math] estimation in WMAP-3yr #hinshaw2007 and by Smith et al (2007)#smith2007 in the detection of CMB lensing in WMAP maps. The different steps of the method used for this study can be summarized as follows:

1. The scanning related information (i.e., statistics of the orientation of each detector within each pixel) is computed first, and only once for a given observation campaign:

   [math] w^d_s({\bf r}_p) = \sum_j e^{i s \psi_j}, \label{eq:e1} [/math]

   where [math]\psi_j[/math] is the orientation of the detector with respect to the local meridian during the measurement $j$ occurring in the direction ${\bf r}_p$. Note that the $s=0$ moment is simply the hit count map. The orientation hit moments are computed up to degree $s=4$. At the same time, the first two moments of the distribution of samples within each pixel (i.e., the centre of mass and moments of inertia) are computed and stored on disc.

2. The scanning beam map or beam model of each detector [math]d[/math] is analyzed into its Spherical Harmonics coefficients

   [math] b^d_{ls} = \int d{\bf r} B_d({\bf r}) Y_{ls}({\bf r})\label{scanningBlm} [/math]

   where [math]B_d(\bf{r})[/math] is the beam map centered on the North pole, and [math]Y_{ls}(\bf{r})[/math] is the Spherical Harmonics basis function. Higher [math]s[/math] indexes describes higher degrees of departure from azimuthal symmetry and, for HFI beams, the coefficients [math]b^d_{ls}[/math] are decreasing functions of [math]s[/math] at most multipoles considered. It also appears that, for [math]l\lt 3000[/math], the coefficients with [math]|s| \gt 4[/math] account for much less of [math]1\%[/math] of the beam solid angle. Spot checks where window functions are computed with $|s|\le 6$ show a difference of less than $10^{-4}$ for $\ell<2000$ at 100 GHz and for $\ell<3000$ at 143 and 217 GHz. For these reasons, only modes with $|s| \le 4$ are considered in the present analysis. Armitage-Caplan & Wandelt (2009)#armitage-caplan2009 reached a similar conclusion in their deconvolution of LFI beams.

3. For a given CMB sky realization $t$, described by its spherical harmonics coefficients $a_{\ell m} = \int d{\bf r} t({\bf r}) Y_{\ell m}({\bf r})$, the $b^d_{\ell s}$ coefficients computed above are used to generate $s$-spin weighted maps,

   [math] m^d_{s}({\bf r}) = \sum_{\ell m} b^d_{\ell s}\ a_{\ell m}\ {}_sY_{\ell m}({\bf r}), \label{eq:e3} [/math]

   as well as the first and second derivatives, using standard HEALPix tools.

4. The spin weighted maps and orientation hit moments of the same order [math]s[/math] are combined for all detectors involved, to provide an “observed” map

   [math] m({\bf r}) = \left(\sum_d \sum_s w^d_s({\bf r}) m^d_s({\bf r})\right) / \sum_d w^d_0({\bf r}). \label{eq:e4} [/math]

   Similarly the local spatial derivatives are combined with the location hit moments to describe the effect of the non-ideal sampling of each pixel (see [sec:pixelization]). In this combination, the respective number of hits of each detector in each pixel is considered, as well as the weighting (generally proportional to the inverse noise variance) applied to each detector in order to minimize the final noise.

5. The power spectrum of this map can then be computed, and compared to the input CMB power spectrum to estimate the effective beam window function over the whole sky, or over a given region of the sky.

Monte-Carlo (MC) simulations in which the sky realizations are changed can be performed by repeating steps 3, 4 and 5. The impact of beam model uncertainties can be studied by including step 2 into the MC simulations.

QuickBeam

For more details, see #planck2013-p03c

Planck observes the sky after convolution with a “scanning beam”, which captures its effective response to the sky as a function of displacement from the nominal pointing direction. Decomposing the scanning beam into harmonic coefficients [math]B_{lm}[/math], each time-ordered data (TOD) sample can be modeled as (neglecting the contribution from instrumental noise, which is independent of beam asymmetry) [math]%T_i = \sum_{lms} D^{l}_{-m s} (\phi_i, \theta_i, \alpha_i) b_{ls} (-1)^{m) T_{lm} + n_i, T_i = \sum_{lms} e^{-i s \alpha_i} B_{ls} \tilde{T}_{lm} {}_s Y_{lm}(\theta_i, \phi_i), \label{eqn:tod_beam}[/math] where the TOD samples are indexed by [math]i[/math], and [math]\tilde{T}_{lm}[/math] is the underlying sky signal. The spin spherical harmonic [math]{}_s Y_{lm}[/math] rotates the scanning beam to the pointing location [math](\theta, \phi)[/math], while the [math]e^{-i s \alpha_i}[/math] factor gives it the correct orientation. Eq. \ref{eqn:tod_beam} may be evaluated with the “TotalConvolver” algorithm of Wandelt and Gorski (2001)#wandelt2001, accelerated using the “conviqt” recursion relations Prezeau and Reinecke (2010)#prezeau2010 This approach is implemented in LevelS, although because it involves working with a TOD-sized objected it is necessarily slow.

On the small angular scales comparable to the size of the beam, it is a good approximation to assume that the procedure of mapmaking from TOD samples is essentially a process of binning: [math]T(p) = \sum_{i \in p} T_i / H(p),\label{eqn:map_beam_full}[/math] where [math]H(p)[/math] is the total number of hits in pixel [math]\hat{n}[/math].

Starting with a normalized, rescaled harmonic transform of the beam [math]B_{lm}[/math], sky multipoles [math]\tilde{T}_{lm}[/math] and a scan history object [math]w(\hat{n}, s)[/math] given by [math]w(\hat{n}, s) = \sum_{j \in p} e^{i s \alpha_j} / H(\hat{n})[/math] where the sum is over all hits [math]j[/math] of pixel [math]p[/math] at location [math]\hat{n}_p[/math], and [math]\alpha_j[/math] is the scan angle for observation [math]j[/math]. The harmonic transform of this scan-strategy object is given by

[math] {}_{s} w_{L M} = \int d^2 \hat{n} {}_s Y_{LM}^*(\hat{n}) w(\hat{n}, s). \label{eq:spin_hits} [/math]

The beam-convolved observation is then given by

[math] \tilde{T}(\hat{n}) = \sum_{slm} w(\hat{n}, -s ) B_{ls} T_{lm} {}_s Y_{lm}(\hat{n}). \label{eq:tilde_T} [/math]

Taking the ensemble average of the pseudo-Cl power spectrum of these [math]T_{lm}[/math] we find

[math] \tilde{C}_{L}^{TT} = \sum_{S S'} \sum_{l_1 l_2} \frac{(2l_1+1)(2l_2+1)}{4\pi} {}_{(-s -s')}{\cal W}_{l_1} B_{l_2 S} B_{l_2 S'}^* C^{TT}_{l_2} \left( \begin{array}{ccc} \! l_1\! & l_2\! & L\! \\ \! s\! & -s\! & 0\! \end{array} \right) \left( \begin{array}{ccc} \! l_1\! & l_2\! & L\! \\ \! s'\! & -s'\! & 0\! \end{array} \right) \label{eq:pseudo_Cl_matrix} [/math]

where [math]{}_{(s s')}{\cal W}_{L} = \frac{1}{2L+1} \sum_{M} {}_{S} w_{LM} {}_{S'} w_{LM}^*[/math] is a cross-power spectrum of scan history objects. Note that the $w(\hat{n}, s )$ which we have used here can also incorporate a position dependent weighting to optimize the pseudo-Cl estimate, such as inverse-noise or a mask– the equations are unchanged. Writing the pseudo-Cl in position space (a la Dvorkin and Smith, 2009dvorkin2008) with Wigner-d matrices we have

[math] \tilde{C}_{L}^{TT} = \frac{1}{8\pi} \sum_{S S'} \int_{-1}^{1} dz \ d^{L}_{00}(z) \left[\sum_{l_1} d^{l_1}_{-s -s'}(z) {}_{(-s -s')}{\cal W}_{l_1} (2l_1+1) \right] \left[ \sum_{l_2} d^{l_2}_{s s'}(z) B_{l_2 S} B_{l_2 S'}^* C^{TT}_{l_2}(2l_2+1) \right]. \label{eq:pseudo_Cl_corr} [/math]

This integral can be implemented exactly using Gauss-Legendre quadrature, with a cost of $\cal 0(l_{\rm max}^2 s_{\rm max}^2)$. For simplicity, the equations here are written for the auto-spectrum of a single detector, but the generalization to a map made by adding several detectors with different weighting is straightforward. The cost to compute all of the necessary terms exactly in that case becomes [math]\cal 0(l_{\rm max}^2 s_{\rm max}^2 N_{\rm det}^2)[/math].

On the flat-sky, beam convolution is multiplication in Fourier space by a beam rotated onto the scan direction. Multiple hits with different scan directions are incorporated by averaging (as the scan history objects above encapsulate).

A scan strategy which is fairly smooth across the sky is nearly equivalent to observing many independent flat-sky patches at high $L$. There is a fairly good approximation to the beam convolved pseudo-power spectrum which is essentially a flat-sky approximation. In the limit that $L \gg \ell_1$, with $C_{\ell_2}$ and $B_{\ell_2}$ is a slowly-varying function in $\ell_2$, and using the equality

\begin{equation} \sum_{\ell_2} (2 \ell_2+1) \left(

   \begin{array}{ccc}
       \! l_1\! & l_2\!  & L\!  \\
       \! s\! & -s\!  & 0\!
     \end{array}
   \right)

\left(

   \begin{array}{ccc}
       \! l_1\! & l_2\!  & L\!  \\
       \! s'\! & -s'\!  & 0\!
     \end{array}
   \right)
= \delta_{ss'},

\end{equation}

the pseudo-$C_\ell$ sum above can be approximated as

[math] {\tilde{C}}_L^{TT} = C_L^{TT} \sum_{M} \left\lt \left| w(\hat{n}_p, M) \right|^2 \right\gt _p |B_{L M}|^2, \label{eq:pseudo_Cl_approx} [/math] where the average $\langle \rangle_p$ is taken over the full sky. It is illustrative to consider two limits of this equation. Firstly, for a ``raster scan strategy in which each pixel is observed with the same direction:

\begin{equation} \left< \left| w(\hat{n}, M) \right|^2 \right>_p = 1, \end{equation}

and the predicted transfer function is just the power spectrum of the beam. Secondly, for a ``best-case scan strategy, in which each pixel is observed many times with many different orientation angles,

\begin{equation} \left< \left| w(\hat{n}, M) \right|^2 \right>_p = \delta_{M0}, \end{equation}

and the transfer function is the azimuthally symmetric part of the beam. Note that this is for a full-sky observation; in the presence of a mask, the average above produces an $f_{\rm sky}$ factor, as expected but neglects the coupling between $L$ multipoles (which can be calculated with the more complete equations above).

Effective beam window functions

The effective beam window functions $B(l)$ for HFI, computed using Quickbeam, are available in the RIMO. They do not contain the pixel window function.

Pixelization Artifacts

For more details, see #planck2013-p03c

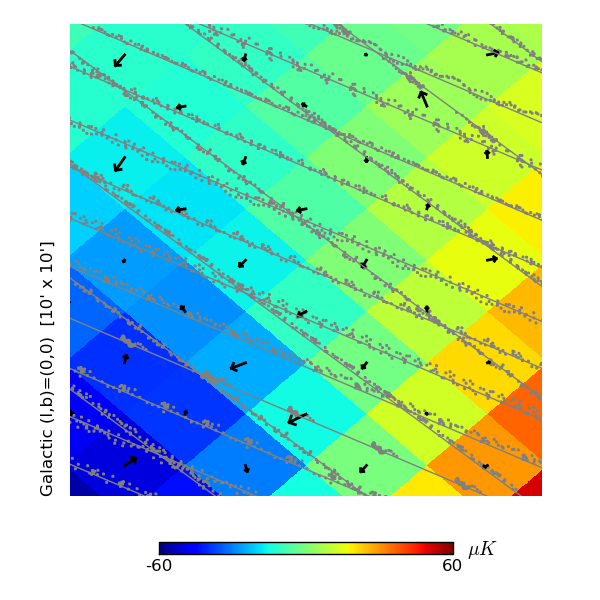
Planck-HFI maps are produced at HEALPix resolution 11 [math](N_{\rm side} = 2048)[/math], corresponding to pixels with a typical dimension of [math]1.7'[/math]. With the resolution comparable to the spacing between scanning rings there is an uneven distribution of hits within pixels, introducing a complication in the analysis and interpretation of the Planck maps. A sample of the Planck distribution of sample hits within pixels is illustrated in Fig. 2.

Figure 2: Illustration of TOI samples near the Galactic plane (gray dots), over-plotted on a simulated CMB realization which has been convolved with a Gaussian 7' FWHM beam and pixelized at $(N_{\rm side} = 2048)$. Associated scanning rings (gray lines) as well as centers of mass for the hit distribution (black arrows) are also plotted.

The collaboration has produced 3 codes which may be used to simulate the effect of pixelization on the observed sky, LevelS/TotalConvoler/Conviqt#reinecke2006 #wandelt2001 #prezeau2010, FeBeCoP#mitra2010, and FICSBell further discussion of the three methods and how they each simulate the pixelization effect..

For the measurement of CMB fluctuations, the effects of pixelization may be studied analytically. On the small scales relevant to pixelization, the observed CMB is smooth, both due to physical damping as well as the convolution of the instrumental beam. Taylor expanding the CMB temperature about a pixel center to second order, the typical gradient amplitude is given by [math]\langle |\nabla T |^2 \rangle = \frac{1}{4\pi} \sum_{l} l(l+1)(2l+1) C_l^{T} W_l \approx 1\times10^9 \mu K^2 / {\rm rad}^2.[/math] where the approximate value is calculated for a [math]\Lambda[/math] CDM cosmology with a [math]7'[/math]FWHM Gaussian beam. The typical curvature of the observed temperature, on the other hand is given by [math]\langle |\nabla^2 T |^2 \rangle = \frac{1}{4\pi} \sum_{l} [l(l+1)]^2(2l+1) C_l^{T} W_l \approx 7\times10^{14} \mu K^2 / {\rm rad}^4.[/math] On the scales relevant to the maximum displacement from the center of a [math]1.7'[/math] pixel, the maximum displacement is [math]{\cal O}(1' = 3\times10^{-4} {\rm rad})[/math], and so the gradient term tends to dominate, although the curvature term is still non-negligible. For each observation of a pixel, we can denote the displacement from the pixel center as [math]d = d_{\theta} + i d_{\phi}[/math]. The average over all hits within a pixel gives an overall deflection vector which we will denote for a pixel center located at [math]\hat{n}[/math] as [math]d(\hat{n})[/math]. This represents the center of mass of the hit distribution; Fig. 2 shows these average deflections using black arrows. The deflection field [math]d(\hat{n})[/math] may be decomposed into spin-1 spherical harmonics as [math]d_{lm} = \int_{4\pi} {}_1 Y_{lm}^* d(\hat{n}).[/math] With a second order Taylor expansion of the CMB temperature about each pixel center, it is then possible to calculate the average pseudo-Cl power spectrum of the pixelized sky. This is given by

[math] C_l^{T} = [1-l(l+1)R^d] {C}_l^{T} W_l + \frac{1}{2} \sum_{l_1 l_2} \frac{l_1(l_1+1)(2l_1+1)(2l_2+1)}{4\pi} \left( \begin{array}{ccc} \! l_1\! & l_2\! & l\! \\ \! l\! & -l\! & 0\! \end{array} \right)^2 C_{l_1}^{T} W_{l_1} \left[ C_{l_2}^{d+} + (-1)^{l + l_1 + l_2} C_{l_2}^{ d-} \right], \label{eqn:clt_pixelized} [/math]

where [math]R^{d} = \langle |d|^2 \rangle/2[/math] is half the mean-squared deflection magnitude (averaged over hits within a pixel, as well as over pixels). [math]C_l^{d+}[/math] is the sum of the gradient and curl power spectra of [math]d_{lm}[/math], and [math]C_l^{d-}[/math] is the gradient spectrum minus the curl spectrum. The [math]R^{d}[/math] term describes a smearing of the observed sky due to pixelization. For uniform pixel coverage of [math]N_{\rm side}=2048[/math] pixels [math]\sqrt{ \langle |d|^2 \rangle } = 0.725'[/math] while, for the hit distribution of Planck frequency maps, [math]R^{d}[/math] is typically within 0.2% of this value for CMB channels, and 0.4% for all channels. This term is therefore accurately described by the HEALPix pixel window function, which is derived under the assumption of uniform pixel coverage, and the resulting relative error on the beam window function is at most [math]4\times 10^{-4}[/math] for [math]\ell \le 3000[/math].

The effect of pixelization is essentially degenerate with that of gravitational lensing of the CMB, with the difference that it (1) acts on the beam-convolved sky, rather than the actual sky and (2) produces a curl-mode deflection field as well as a gradient mode. This is discussed further in the Planck gravitational lensing#planck2013-p12 paper, where the subpixel deflection field constitutes a potential source of bias for the measured lensing potential. Indeed, Eq. \ref{eqn:clt_pixelized} is just a slightly modified version of the usual first order CMB lensing power spectrum Hu (2000)#Hu2000, Lewis and Challinor (2006)#Lewis2006 to accommodate curl modes.

A useful approximation to Eq. \ref{eqn:clt_pixelized} which is derived in the unrealistic limit that the deflection vectors are uncorrelated between pixels, but in practice gives a good description of the power induced by the pixelization, is that the [math]d(\hat{n})[/math] couples the CMB gradient into a source of noise with an effective level given by [math]\sigma^{N} \approx \sqrt{ R^T \frac{4\pi}{N_{\rm pix}} \langle | d(\hat{n}) |^2 \rangle }, % (\muKarcmin ),[/math]

where the average is taken over all pixels and [math]R^T[/math] is half the mean-squared power in the CMB gradient: [math]R^{T} = \frac{1}{8\pi} \sum_{l} l(l+1)(2l+1) \tilde{C}_l^{T}.[/math] For frequency-combined maps, [math]\sqrt{ \langle | d(\hat{n}) |^2 \rangle }[/math] is typically on the order of [math]0.1'[/math], and so the induced noise is at the level of [math]\sigma^{N} \sim 2 \mu[/math]K arcmin. This is small compared to the instrumental contribution, although it does not disappear when taking cross-spectra, depending on how coherent the hit distributions of the two maps in the cross-spectrum are.

References

<biblio force=false>

1. References
2. References2

</biblio>