LFI systematic effect uncertainties

Overview

Known systematic effects in the Planck-LFI data can be divided into two broad categories: effects independent of the sky signal, which can be considered as additive or multiplicative spurious contributions to the measured timelines, and effects which are dependent on the sky and that cannot be considered independently from the observation strategy.

Here we report a brief summary of these effects, all the details can be found in Planck-2013-III and Planck-2015-A04.

Summary of uncertainties due to systematic effects

In this section we provide a top-level overview of the uncertainties due to systematic effects in the Planck-LFI CMB temperature maps and power spectra. Table 1 provides a list of these effects with short indications of their cause, strategies for removal and references to sections and/or papers where more information is found.

Table 1. List of known instrumental systematic effects in Planck LFI.

Effect	Source	Control/Removal	Reference
Effects independent of sky signal (T and P)
White noise correlation	Phase switch imbalance	Diode weighting	Planck-2013-III
1/[math]f[/math] noise	RF amplifiers	Pseudo-correlation and destriping	Planck-2013-III
Bias fluctuations	RF amplifiers, back-end electronics&	Pseudo-correlation and destriping	DPC paper
Thermal fluctuations	4 K, 20 K and 300 K thermal stages	Calibration, destriping	DPC paper
1 Hz spikes	Back-end electronics	Template fitting and removal	DPC paper
Effects dependent on sky signal (T and P)
Main beam ellipticity	Main beams	Accounted for in window function	DPC paper
Near sidelobes pickup	Optical response at angles [math] \lt 5^\circ[/math] from the main beam	Masking of Galaxy and point sources	DPC paper
Far sidelobes pickup	Main and sub-reflector spillovers	Model sidelobes removed from timelines	DPC paper
Analogue-to-digital converter non linearity	Back-end analogue-to-digital converter	Template fitting and removal	DPC paper
Imperfect photometric calibration	Sidelobe pickup, radiometer noise temperature changes and other non-idealities	Calibration using the 4 K reference load voltage output	DPC paper
Pointing	Uncertainties in pointing reconstruction, thermal changes affecting focal plane geometry	Negligible impact anisotropy measurements	DPC paper
Effects specifically impacting polarization
Bandpass asymmetries	Differential orthomode transducer and receiver bandpass response	Spurious polarisation removal	DPC paper
Polarization angle uncertainty	Uncertainty in the polarization angle in-flight measurement	Negligible impact	DPC paper
Orthomode transducer cross-polarization	Imperfect polarization separation	Negligible impact	DPC paper

The impact of 1/[math]f[/math] noise has been assessed using half-ring noise maps normalised to the white noise estimate at each pixel obtained from the white noise covariance matrix, so that a perfectly white noise map would be Gaussian and isotropic with unit variance. Deviations from unity trace the contribution of residual 1/f noise in the final maps, which ranges from 0.06% at 70 GHz to 2% at 30 GHz. Pixel uncertainties due to other systematic effects have been calculated on simulated maps degraded at N_side = 128 at 30 and 44 GHz and N_side = 256 at 70 GHz in order to approximate the optical beam size. This downgrading has been applied in all cases a systematic effect has been evaluated at map level.

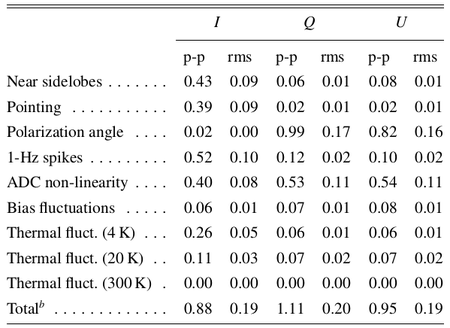
In Table 2 we list the r.m.s. and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as peak-to-peak (p-p) difference although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map.

Table 2. Summary of systematic effects uncertainties on maps in μK_CMB.

30 GHz	44 GHz	70 GHz

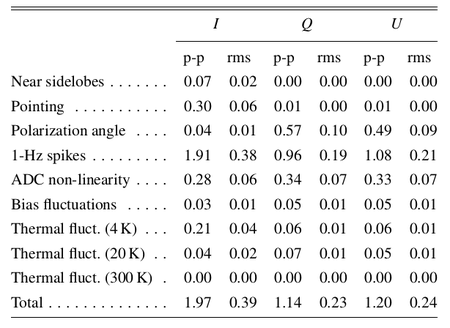
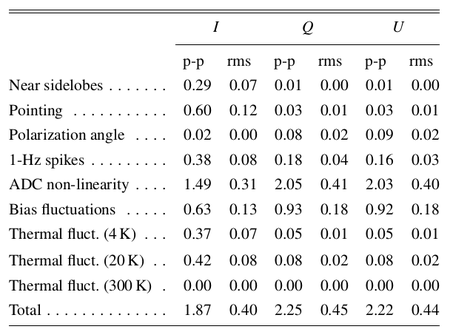
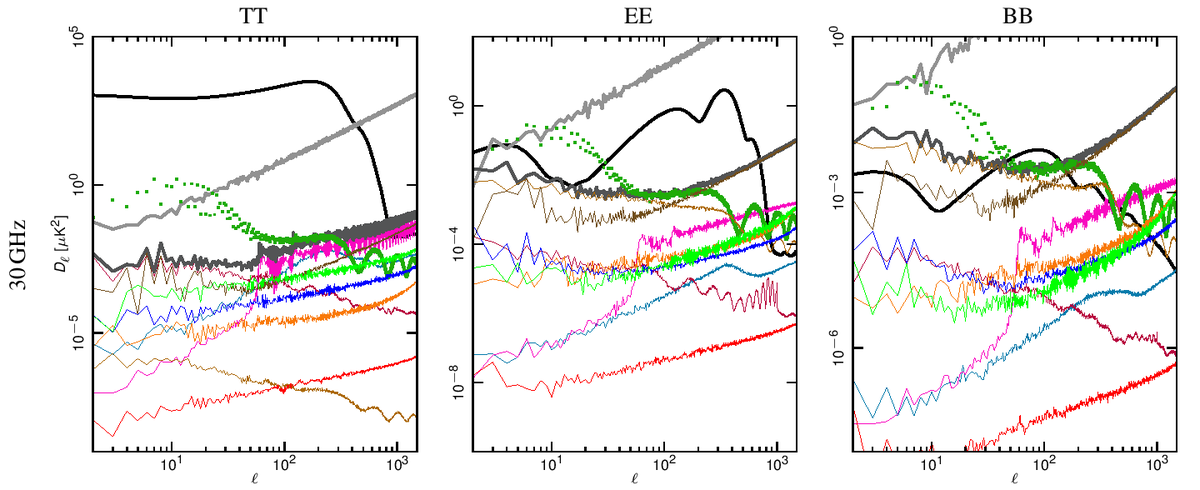
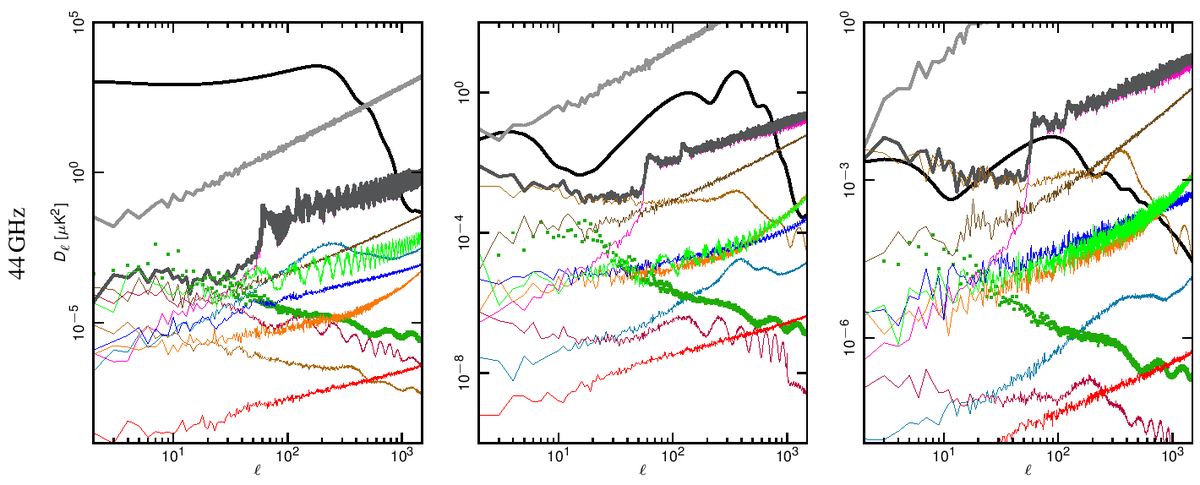
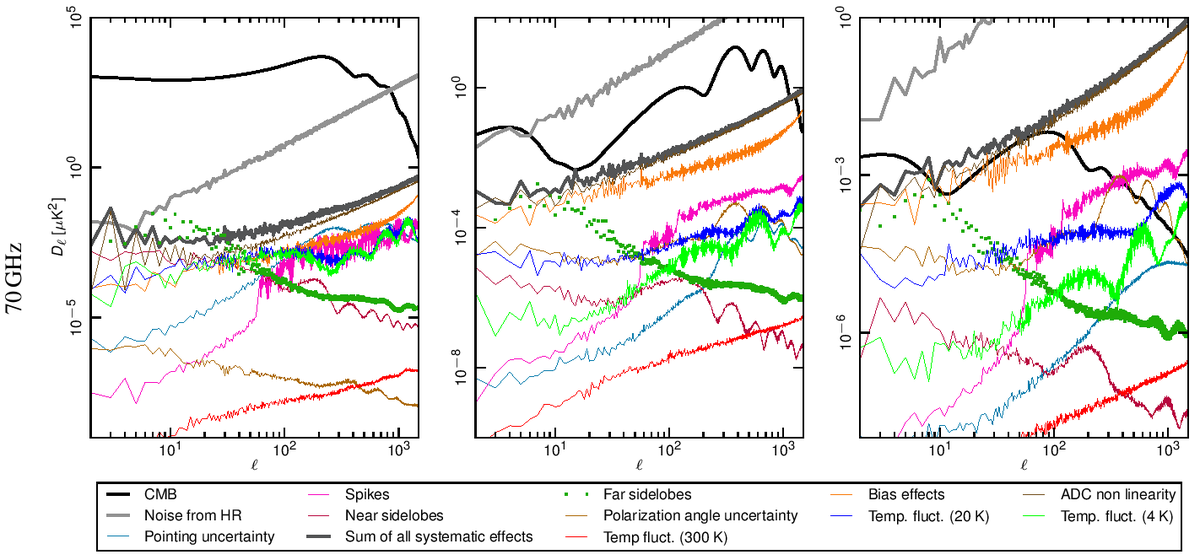
Angular power spectra have been obtained from full resolution (N_side = 1024) systematic effect maps at each frequency using HEALPix Anafast . In Fig. 1 we show how the power spectrum of the various effects compared with the Planck best-fit spectra and with the noise level coming from the half-ring difference maps.

Our assessment shows that the global impact of systematic effects uncertainties in the LFI do not limit either temperature or E-mode spectra measurements.

Figure 1. Angular power spectra of the various systematic effects compared to the Planck beam-filtered temperature and polarization spectra. The dark-gray thick curve represents the total contribution. The dark-green dotted curve represent the contribution from far sidelobes that has been removed from the data and, therefore not considered in the total. The CMB TT and EE curves correspond to the Planck best-fit power spectra. The theoretical $B$-mode CMB spectrum assumes a tensor-to-scalar ratio r = 0.1, a tensor spectral index nT=0 and has not been beam-filtered. Rows: 30, 44 and 70 GHz spectra. Columns: temperature, E-mode and B-mode spectra. .

Effects independent of sky signal

Noise correlations and 1/f noise

TBW

Thermal effects

TBW

Bias fluctuations

TBW

1-Hz spikes

TBW

Main Beam Ellipticity

TBW

Near Sidelobes pickup

TBW

Effects dependent on sky signal

Sidelobe pick-up

TBW

ADC non linearity

TBW

Pointing effects

TBW

Polarization Angle Uncertainty

TBW

Ortho-Mode Transducer Cross-Polarization

TBW