CMB spectrum & Likelihood Code

CMB spectra

General description

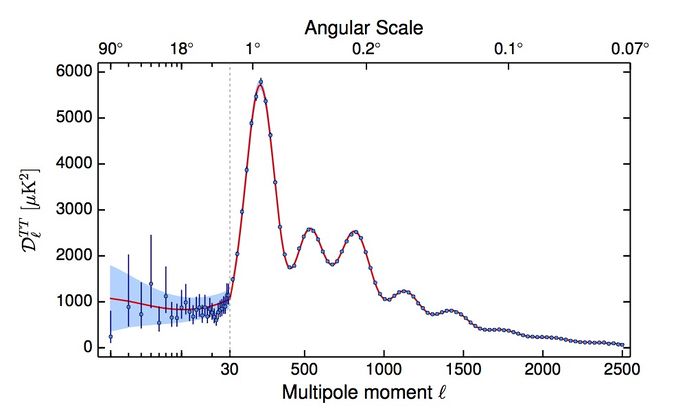
The Planck best-fit CMB temperature power spectrum, shown in figure below, covers the wide range of multipoles [math] \ell [/math] = 2-2508. UPDATE COMMANDER: Over the multipole range [math] \ell [/math] = 2–29, the power spectrum is derived from a component-separation algorithm, Commander: applied to maps in the frequency range 30–353 GHz over 91% of the sky Planck-2013-XII . The asymmetric error bars associated to this spectrum are the 68% confidence limits and include the uncertainties due to foreground subtraction.

For multipoles equal or greater than [math]\ell=30[/math], instead, the spectrum is derived from the Plik likelihood Planck-2015-A11 by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds. Associated 1-sigma errors include beam uncertainties. Both Commander and Plik are described in more details in the sections below.

CMB spectrum. Logarithmic x-scale up to [math]\ell=30[/math], linear at higher [math]\ell[/math]; all points with error bars. The red line is the Planck best-fit primordial power spectrum (cf Planck TT+lowP in Table 3 of Planck-2015-A13). The blue shaded area shows the uncertainties due to cosmic variance alone.

Production process

UPDATE COMMANDER The [math]\ell[/math] < 50 part of the Planck power spectrum is derived from the Commander approach, which implements Bayesian component separation in pixel space, fitting a parametric model to the data by sampling the posterior distribution for the model parameters Planck-2013-XII. The power spectrum at any multipole [math]\ell[/math] is given as the maximum probability point for the posterior [math]C_\ell[/math] distribution, marginalized over the other multipoles, and the error bars are 68% confidence level Planck-2013-XV.

The [math]\ell[/math] > 30 part of the CMB temperature power spectrum has been derived by the Plik likelihood, a code that implements a pseudo-Cl based technique, extensively described in Sec. 2 and the Appendix of Planck-2013-XV. Frequency spectra are computed as cross-spectra between half-mission maps. Mask and multipole range choices for each frequency spectrum are summarized in Section 3.3 of Planck-2015-A13 and in Planck-2015-A11. The final power spectrum is an optimal combination of the 100, 143, 143x217 and 217 GHz spectra, corrected for the best-fit unresolved foregrounds and inter-frequency calibration factors, as derived from the full likelihood analysis (cf Planck+TT+lowP in Table 3 of Planck-2015-A13). A thorough description of the models of unresolved foregrounds is given in Planck-2015-A11. The spectrum covariance matrix accounts for cosmic variance and noise contributions, together with beam uncertainties. The [math]\ell[/math] > 30 CMB TT spectrum and associated covariance matrix are available in two formats:

1. Unbinned, with 2479 bandpowers ([math]\ell=30-2508[/math]).
2. Binned, in bins of [math] \Delta\ell=30 [/math], with 83 bandpowers in total. We bin the [math] C_\ell [/math] power spectrum with a weight proportional to [math] \ell (\ell+1) [/math], so that the [math] C_{\ell_b} [/math] binned bandpower centered in [math] \ell_b [/math] is: [math] \\ C_{\ell_b}=\Sigma_{\ell \in b} w_{\ell_b\ell} C_\ell \quad \text{with} \quad w_{\ell_b\ell}=\frac{\ell (\ell+1)}{\Sigma_{\ell \in b} \ell (\ell+1)}. \\[/math] Equivalently, using the matrix formalism, we can construct the binning matrix B as: [math]\\ B_{\ell \ell_b}=w_{\ell_b\ell} \\ [/math] where B is a [math] n_b\times n_\ell[/math] matrix, with [math]n_b=83[/math] the number of bins and [math]n_\ell=2479[/math] the number of unbinned multipoles. Thus: [math] \\ \vec{C}_\mathrm{binned}=B \, \vec{C} \\ \mathrm{cov_\mathrm{binned}}= B\, \mathrm{cov}\, B^T \\ \ell_b=B\, \ell \\ [/math] Here, [math] \vec{C}_{binned} (\vec{C}) [/math] is the vector containing all the binned (unbinned) [math]C_\ell[/math] bandpowers, [math]\mathrm{cov} [/math] is the covariance matrix and [math]\ell_b[/math] is the weighted multipole average in each bin. The binned [math]D_{\ell_B}[/math] power spectrum is then calculated as: [math] \\ D_{\ell_b}=\ell_b (\ell_b+1)/2/\pi C_{\ell_b} [/math].

Inputs

UPDATE COMMANDER

Low-l spectrum ([math]\ell \lt 30[/math])

• frequency maps from 30–353 GHz
• common mask Planck-2013-XII
• compact sources catalog

High-l spectrum ([math]30 \lt \ell \lt 2500[/math])

• 100, 143, 143x217 and 217 GHz spectra and their covariance matrix (Sec. 3.3 Planck-2015-A13)
• best-fit foreground templates and inter-frequency calibration factors (Table 3 of Planck-2015-A13)
• Beam transfer function uncertainties Planck-2015-A07

File names and Meta data

CHECK EXTENSION NAMES

The CMB spectrum and its covariance matrix are distributed in a single FITS file named

• COM_PowerSpect_CMB_R1.10.fits

which contains 5 extensions

LOW-ELL (BINTABLE)

with the low ell part of the spectrum, not binned, and for l=2-49. The table columns are

1. ELL (integer): multipole number
2. D_ELL (float): $D_l$ as described below
3. ERRUP (float): the upward uncertainty
4. ERRDOWN (float): the downward uncertainty

HIGH-ELL (BINTABLE)

with the high-ell part of the spectrum, binned into 83 bins covering [math]\langle l \rangle = 47-2499\ [/math] in bins of width [math]l=30[/math] (with the exception of the last bin that is smaller). The table columns are as follows:

1. ELL (integer): mean multipole number of bin
2. L_MIN (integer): lowest multipole of bin
3. L_MAX (integer): highest multipole of bin
4. D_ELL (float): $D_l$ as described below
5. ERR (float): the uncertainty

COV-MAT (IMAGE)

with the covariance matrix of the high-ell part of the spectrum in a 83x83 pixel image, i.e., covering the same bins as the HIGH-ELL table.

HIGH-ELL (BINTABLE)

with the high-ell part of the spectrum, unbinned, in 2979 bins covering [math]\langle l \rangle = 30-2508\ [/math]. The table columns are as follows:

1. ELL (integer): multipole
2. D_ELL (float): $D_l$ as described below
3. ERR (float): the uncertainty

COV-MAT (IMAGE)

with the covariance matrix of the high-ell part of the spectrum in a 2979x2979 pixel image, i.e., covering the same bins as the HIGH-ELL table.

The spectra give $D_\ell = \ell(\ell+1)C_\ell / 2\pi$ in units of $\mu\, K^2$, and the covariance matrix is in units of $\mu\, K^4$.

The CMB spectrum is also given in a simple text comma-separated file:

• COM_PowerSpect_CMB_R1.10.txt

Likelihood

TO BE WRITTEN.