Difference between revisions of "Frequency maps angular power spectra"
(→Production process) |
(→Production process) |
||
| (77 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
| + | {{DISPLAYTITLE:Sky temperature power spectra}} | ||
<span style="color:Red"> | <span style="color:Red"> | ||
| − | = HFI | + | == HFI maps power spectra == |
| − | + | Angular power spectra of cut sky CMB dominated maps are provided to allow independent cosmological analysis at high <math>\ell</math>. | |
| − | < | ||
| − | + | ===Product description=== | |
| − | + | The auto and cross-spectra of the 13 [[Frequency Maps#Types of maps | detector set ]] (detset) maps at 100, 143 and 217 GHz, all analyzed on the same 42.8% of the sky, are provided. | |
| − | + | The mask used is apodized to reduce the power leakage from large scale to small scale (see input section). Except for the removal of the most contaminated pixels through masking, no attempt at astrophysical components separation has been performed. | |
| − | + | For each pair of detectors <math>X</math> and <math>Y</math>, are provided, | |
| − | + | * the unbinned ''estimated'' power spectrum <math>\hat{C}^{XY}_\ell</math> for all <math>\ell</math> from 0 to 3508 (see [[#all_dscl|Figure 1]] below), as well as | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | For each pair of detectors | ||
| − | * the unbinned power spectrum | ||
* the unbinned symmetric covariance matrix | * the unbinned symmetric covariance matrix | ||
\begin{align} | \begin{align} | ||
| − | M^{XY}_{\ell \ell'} \equiv \langle\Delta C^{XY}_\ell\Delta C^{XY}_{\ell'}\rangle | + | \hat{M}^{XY}_{\ell \ell'} \equiv \langle\Delta \hat{C}^{XY}_\ell\Delta \hat{C}^{XY}_{\ell'}\rangle |
\label{eq:covmatCl} | \label{eq:covmatCl} | ||
\end{align} | \end{align} | ||
| − | for all | + | for all <math>\ell</math> on the same range. At the price of some extra hypotheses, that information can be used to build the likelihood of a given theoretical power spectrum <math>C_{\ell}</math> given the data, and therefore determine the best cosmological models fitting the data. Several examples of such high-<math>\ell</math> likelihoods are described, discussed and compared in {{PlanckPapers|planck2013-p08}}. |
$ | $ | ||
| Line 36: | Line 24: | ||
\newcommand{\lmax}{\ell_{\mathrm{max}}} | \newcommand{\lmax}{\ell_{\mathrm{max}}} | ||
$ | $ | ||
| − | Note that | + | Note that <math>\hat{\bfM}</math> only describes the statistical covariance of the power spectrum |
induced by the signal and noise of the input map on the cut sky begin analyzed. | induced by the signal and noise of the input map on the cut sky begin analyzed. | ||
| − | Most sources of systematic effects (such as uncertainty on the beam modeling) as well as post-processing steps (such as foreground subtraction) will increase the covariance. In the particular case of the uncertainty on the beam window functions | + | Most sources of systematic effects (such as uncertainty on the beam modeling) as well as post-processing steps (such as foreground subtraction) will increase the covariance. In the particular case of the uncertainty on the beam window functions <math>B(l)</math>, |
| − | the [[The RIMO|RIMO]] provides for each pair | + | the [[The RIMO|RIMO]] provides for each pair <math>XY</math> a set of eigen-vectors <math>E_{p}^{XY}(\ell)</math> of the relative error on <math>B^{XY}_{\ell}</math> (see {{PlanckPapers|planck2013-p03c|1|HFI time response and beams paper}}), defined for <math>p</math> in <math>[1,5]</math> and <math>\ell</math> in <math>[0, \lmax]</math> (with <math>\lmax</math> being 2500, 3000 or 4000 when the lowest of the nominal frequencies of the detectors <math>X</math> and <math>Y</math> is respectively 100, 143 or 217GHz). The extra contribution to the covariance of <math>C^{XY}_\ell</math> is then |
\begin{align} | \begin{align} | ||
| − | \ | + | \hat{M}^{XY, \mathrm{beam}}_{\ell_1 \ell_2} = 4 \hat{C}^{XY}_{\ell_1} \hat{C}^{XY}_{\ell_2} \sum_{p=1}^{5} E^{XY}_p(\ell_1) E^{XY}_p(\ell_2). |
| + | \label{eq:covmatBeam} | ||
\end{align} | \end{align} | ||
| − | |||
| − | |||
| − | |||
| − | <!-- < | + | <!-- =================================================== --> |
| − | + | <div id="all_dscl"> | |
| − | + | [[File:all_dscl.png | 500px | center | thumb | '''Figure 1:''' The 91 auto- (dotted lines) and cross- (solid lines) angular power spectra <math>\hat{C}_\ell</math>, shown here after a binning of <math>\Delta \ell = 31</math>, grouped by frequencies. For instance the top left panel, tagged ''100x100 (3)'', contains the three spectra 100-ds1x100-ds2, 100-ds1x100-ds1 and 100-ds1x100-ds2. The auto spectra are contaminated at high <math>\ell</math> by the instrumental noise, and all of them may be affected by foreground contamination. The grey circles show the best Planck CMB high-<math>\ell</math> power spectrum described in the [[CMB spectrum & Likelihood Code | CMB spectrum & Likelihood Code section]] ]] | |
| − | + | </div> | |
| − | + | <!-- =================================================== --> | |
| − | |||
| − | |||
| − | + | ====Auto and Cross Power Spectra==== | |
| − | The spectra computed up to | + | The spectra computed up to <math>l=3508</math> using [http://prof.planck.fr/article141.html PolSpice]{{BibCite|Szapudi2001}}{{BibCite|Chon2004}} |
| − | + | are corrected from the effect of the cut sky, and from the nominal beam window function and average pixel function. The different steps of the calculation are | |
| − | + | * computation of the Spherical Harmonics coefficients of the masked input maps <math>\Delta T^X(p)</math> and of the input mask <math>w(p)</math>, | |
| − | |||
| − | are corrected from the effect of the cut sky, and from the nominal beam window | ||
| − | function and average pixel function. The different steps of the calculation are | ||
| − | * computation of the Spherical Harmonics coefficients of the masked input maps | ||
\begin{align} | \begin{align} | ||
| − | \tilde{a}^X_{\ell m} = \sum_p \Omega_p\, \Delta T^X(p)\, w(p)\, Y^*_{\ell m}(p), | + | \tilde{a}^X_{\ell m} = \sum_p \Omega_p\, \Delta T^X(p)\, w(p)\, Y^*_{\ell m}(p), \label{eq:almdef} |
\end{align} | \end{align} | ||
\begin{align} | \begin{align} | ||
| − | \tilde{w}_{\ell m} = \sum_p \Omega_p\ w(p)\, Y^*_{\ell m}(p); | + | \tilde{w}^{(n)}_{\ell m} = \sum_p \Omega_p\ w^n(p)\, Y^*_{\ell m}(p); \label{eq:wlmdef} |
\end{align} | \end{align} | ||
| − | where the sum is done over all sky pixels | + | where the sum is done over all sky pixels <math>p</math>, <math>\Omega_p</math> is the pixel area, and <math>n</math> is either 1 or 2; |
| − | * the sky (cross or auto) pseudo-power spectrum and mask power spectrum are computed from the | + | * the sky (cross or auto) pseudo-power spectrum and mask power spectrum are computed from the <math>\tilde{a}_{\ell m}</math> and <math>\tilde{w}_{\ell m}</math>, |
\begin{align} | \begin{align} | ||
| − | \tilde{C}^{XY}_\ell = \sum_{\ell m} \tilde{a}^X_{ m} \tilde{a}^{Y^*}_{\ell m} / (2 \ell + 1), | + | \tilde{C}^{XY}_\ell = \sum_{\ell m} \tilde{a}^X_{ m} \tilde{a}^{Y^*}_{\ell m} / (2 \ell + 1), \label{eq:alm2cl} |
\end{align} | \end{align} | ||
\begin{align} | \begin{align} | ||
| − | \tilde{W}_\ell = \sum_{\ell m} \tilde{w}_{ m} \tilde{w}^*_{\ell m} / (2 \ell + 1); | + | \tilde{W}^{(n)}_\ell = \sum_{\ell m} \tilde{w}^{(n)}_{ m} {\tilde{w}^{(n)}}^*_{\ell m} / (2 \ell + 1); \label{eq:wlm2wl} |
\end{align} | \end{align} | ||
* the sky and mask angular correlation function are computed from the respective power spectra, | * the sky and mask angular correlation function are computed from the respective power spectra, | ||
| Line 83: | Line 63: | ||
\end{align} | \end{align} | ||
\begin{align} | \begin{align} | ||
| − | \tilde{\xi}_W(\theta) = \sum_\ell \frac{2\ell+1}{4\pi} \tilde{W}_{\ell} P_\ell(\theta) | + | \tilde{\xi}_W(\theta) = \sum_\ell \frac{2\ell+1}{4\pi} \tilde{W}^{(1)}_{\ell} P_\ell(\theta), |
\end{align} | \end{align} | ||
| + | where <math>P_\ell</math> is the Legendre Polynomial of order <math>\ell</math>; | ||
* the ratio of the sky angular correlation by the mask correlation provides the cut sky corrected angular correlation, | * the ratio of the sky angular correlation by the mask correlation provides the cut sky corrected angular correlation, | ||
\begin{align} | \begin{align} | ||
| − | \xi(\theta) = \tilde{\xi}(\theta) / \tilde{\xi}_W(\theta); | + | \xi(\theta) = \tilde{\xi}(\theta) / \tilde{\xi}_W(\theta); \label{eq:xi_deconv} |
\end{align} | \end{align} | ||
* the sky angular correlation function which is then turned into a angular power spectrum, | * the sky angular correlation function which is then turned into a angular power spectrum, | ||
\begin{align} | \begin{align} | ||
| − | {C}_\ell = 2\pi \sum_i w_i \xi(\theta_i) P_\ell(\theta_i) \label{eq:xi2cl} | + | {C'}_\ell = 2\pi \sum_i w_i \xi(\theta_i) P_\ell(\theta_i), \label{eq:xi2cl} |
\end{align} | \end{align} | ||
| − | * the resulting power spectrum is corrected from the nominal beam window function | + | where <math>w_i</math> are the weights of the Gauss-Legendre quadrature, for <math>\theta</math> in <math>[0, \pi]</math>; |
| + | * the resulting power spectrum is corrected from the nominal beam window function <math>B_\ell</math> and average pixel window function <math>w_{\mathrm{pix}}(\ell)</math>, to provide the final Spice estimator <math>\hat{C}_\ell</math>, | ||
\begin{align} | \begin{align} | ||
| − | \hat{C}_\ell = {C}_\ell / \left( B^2_\ell w^2_{\mathrm{pix}} \right). | + | \hat{C}_\ell = {C'}_\ell / \left( B^2_\ell w^2_{\mathrm{pix}}(\ell) \right). \label{eq:clfinal} |
\end{align} | \end{align} | ||
| + | ====Covariance Matrices==== | ||
| + | The covariance matrix for the pair <math>XY</math> is computed by PolSpice | ||
| + | using the formalism described in{{BibCite|Efstathiou2004}}<!--[http://adsabs.harvard.edu/abs/2004MNRAS.349..603E Efstathiou (2004)]-->, also sketched in the appendix | ||
| + | of {{PlanckPapers|planck2013-p08|1|CMB power spectra and likelihood paper}}, assuming the instrumental noise to be white and uniform. | ||
| − | + | $ | |
| − | + | \newcommand{\hC}{\hat C} | |
| − | of | + | $ |
| + | One note that a good approximation of the covariance matrix <math>\tilde{M}</math> of the pseudo <math>\tilde{C}_{\ell}</math> is related to the underlying ''estimated'' auto- and cross-spectra <math>\hC_{\ell}</math> through | ||
| + | \begin{align} | ||
| + | \tilde{M}_{\ell_1\ell_2} \equiv \langle\Delta \tilde{C}^{XY}_{\ell_1}\Delta \tilde{C}^{XY}_{\ell_2}\rangle = | ||
| + | \left( \left(\hC^{XX}_{\ell_1} \hC^{YY}_{\ell_1} \hC^{XX}_{\ell_2} \hC^{YY}_{\ell_2}\right)^{1/2} | ||
| + | + \hC^{XY}_{\ell_1} \hC^{XY}_{\ell_2} \right) | ||
| + | \sum_{\ell_3} \frac{2\ell_3+1}{4\pi} \tilde{W}^{(2)}_{\ell_3} \left( | ||
| + | \begin{array}{ccc} | ||
| + | \! \ell_1\! & \ell_2\! & \ell_3\! \\ | ||
| + | \! 0 \! & 0 \! & 0 \! | ||
| + | \end{array} | ||
| + | \right)^2, | ||
| + | \label{eq:covpseudo} | ||
| + | \end{align} | ||
| + | where <math>\tilde{W}^{(2)}_{\ell}</math> is the power spectrum of the square of the pixel mask (Eqs. \ref{eq:wlmdef} and \ref{eq:wlm2wl} for <math>n=2</math>). The covariance matrix <math>\hat{M}</math> | ||
| + | of the Spice estimator is then computed by applying Eqs. \ref{eq:cl2xi}, \ref{eq:xi_deconv}, \ref{eq:xi2cl} and \ref{eq:clfinal} on each row and column of <math>\tilde{M}</math>. | ||
| − | |||
| − | |||
| − | + | <!-- The products described here, spectra <math>{\hat C}_{\ell}</math> and covariances <math>{\hat M}_{\ell \ell'}</math> can be used to | |
| − | <!-- < | + | estimate the high-<math>\ell</math> likelihood of a given theoretical model given the data available. --> |
| − | the | ||
| − | |||
| − | |||
| − | + | ===Inputs=== | |
| − | + | ; Maps | |
| − | + | : The input maps are the 13 HFI detset (see [[Frequency_Maps#Types_of_maps | ''Type of maps'']] section for details) maps available at 100, 143 and 217 GHz. These are the same as the ones used for high-ell part of the [[CMB spectrum & Likelihood Code | likelihood code]], but that code applies different masks for each cross-spectra in order to minimize further the foreground contamination. | |
| − | + | ; Sky mask | |
| − | + | : All maps were analyzed on the 42.8% of the sky defined by the apodized mask ''HFI_PowerSpect_Mask_2048_R1.10.fits'', which masks out Galactic Plane and point sources (see {{PlanckPapers|planck2013-p08}}), and which is shown in [[#mask_Cl|Figure 2]] below | |
| − | All maps were analyzed on the | ||
| − | < | + | <div id="mask_Cl"> |
| − | + | [[File:mask_Cl.png | 500px | center | thumb | '''Figure 2:''' Apodized pixel mask used for HFI power spectrum estimation ]] | |
| − | + | </div> | |
| − | |||
| − | |||
| − | + | ; Beam Window Function | |
| − | + | : The beam window functions <math>B(l)</math>, and their uncertainties, are the ones used in the high-ell likelihood analysis, described in section 6.1 "Error Eigenmodes" of {{PlanckPapers|planck2013-p08}} and provided in the HFI [[The RIMO|RIMO]]. | |
| − | The beam window functions B(l), and their uncertainties, are the ones used in the | ||
| − | high-ell likelihood analysis, described in section 6.1 "Error Eigenmodes" of | ||
| − | ==Related products== | + | ===Related products=== |
| − | + | None | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ===FITS file structure=== | ||
Power spectra are provided for the auto and cross products built from the 13 detsets available at 100, 143 and 217 GHz, namely: | Power spectra are provided for the auto and cross products built from the 13 detsets available at 100, 143 and 217 GHz, namely: | ||
* 100-ds1, 100-ds2, | * 100-ds1, 100-ds2, | ||
| Line 148: | Line 132: | ||
| − | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" | + | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" width=800px |
| + | |+ '''Power spectrum file data structure''' | ||
| + | |- bgcolor="ffdead" | ||
| + | !colspan="4" | 1. EXTNAME = 'POW-SPEC' (BINTABLE) | ||
| + | |- bgcolor="ffdead" | ||
! Column Name || Data Type || Units || Description | ! Column Name || Data Type || Units || Description | ||
|- | |- | ||
| − | + | |TEMP_CL || Real*4 || <math>\mu</math>K<sub>cmb</sub><sup>2</sup>|| the power spectrum | |
|- | |- | ||
| − | | | + | |TEMP_CL_ERR || Real*4 || <math>\mu</math>K<sub>cmb</sub><sup>2</sup> || estimate of the uncertainty in the power spectrum |
| + | |- bgcolor="ffdead" | ||
| + | ! Keyword || Data Type || Value || Description | ||
|- | |- | ||
| − | | | + | |LMIN || Integer || 0 || First monopole |
|- | |- | ||
| − | !colspan="4"| | + | |LMAX || Integer || value || Last monopole |
| + | |- bgcolor="ffdead" | ||
| + | !colspan="4" | 2. EXTNAME = 'PSCOVMAT' (IMAGE) | ||
|- | |- | ||
| − | | | + | |COVMAT || Real*4 || <math>\mu</math>K<sub>cmb</sub><sup>4</sup> || the covariance matrix |
|- | |- | ||
| − | | | + | |- bgcolor="ffdead" |
| + | ! Keyword || Data Type || Value || Description | ||
|- | |- | ||
| − | + | |NAXIS1 || Integer || dim1 || matrix first dimension | |
|- | |- | ||
| − | | | + | |NAXIS2 || Integer || dim2 || matrix second dimension |
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| + | where LMAX is the same for both vectors, and dim1 = dim2 = LMAX+1 by construction. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===List of filenames=== | ===List of filenames=== | ||
| + | {| align="center" style="text-align:left" border="1" cellpadding="2" cellspacing="0" width=400px | ||
| + | |+ '''FITS filenames''' | ||
| + | |- bgcolor="ffdead" | ||
| + | ! Auto power spectra | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-ds2_R1.10.fits | ||
| + | |- bgcolor="ffdead" | ||
| + | ! Cross power spectra | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x100-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x143-5_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x143-6_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x143-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x143-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds1x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x143-5_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x143-6_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x143-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x143-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_100-ds2x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x143-6_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-5x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-6x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-7x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x143-5_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x143-6_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x143-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds1x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x143-5_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x143-6_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x143-7_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x217-1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_143-ds2x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-1x217-2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-1x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-1x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-1x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-1x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-2x217-3_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-2x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-2x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-2x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-3x217-4_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-3x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-3x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-4x217-ds1_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-4x217-ds2_R1.10.fits | ||
| + | |- | ||
| + | | HFI_PowerSpect_217-ds1x217-ds2_R1.10.fits | ||
| + | |- bgcolor="ffdead" | ||
| + | ! Sky mask | ||
| + | |- | ||
| + | | {{PLASingleFile|fileType=map|name=HFI_PowerSpect_Mask_2048_R1.10.fits|link=HFI_PowerSpect_Mask_2048_R1.10.fits}} | ||
| + | |} | ||
| + | The full list of HFI power spectra with links to the files in the PLA can be found {{PLASpec|inst=HFI|link=here}}. | ||
| − | + | == LFI maps power spectra == | |
| − | + | ===Product description=== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | = LFI | ||
| − | |||
| − | |||
| − | ==Product description== | ||
The angular power spectrum provides information about the distribution of power on the sky map at the various angular scales. It is especially important for CMB, because it is characterized by a number of features, most notably the acoustic peaks, that encode the dependence from cosmological parameters. Therefore, angular power spectra are the basic inputs for the [[CMB spectrum & Likelihood Code | Planck Likelihood Code]], and for estimation of cosmological parameters in general. | The angular power spectrum provides information about the distribution of power on the sky map at the various angular scales. It is especially important for CMB, because it is characterized by a number of features, most notably the acoustic peaks, that encode the dependence from cosmological parameters. Therefore, angular power spectra are the basic inputs for the [[CMB spectrum & Likelihood Code | Planck Likelihood Code]], and for estimation of cosmological parameters in general. | ||
For this release we have computed only temperature power spectra. Polarization is not included. | For this release we have computed only temperature power spectra. Polarization is not included. | ||
| − | Please note that these spectra come from frequency maps. No component separation has been applied, and we have only masked Galactic Plane and detected point sources. Units are <math> \mu K^2_{CMB} </math>. | + | Please note that these spectra come from frequency maps. No component separation has been applied, and we have only masked Galactic Plane and detected point sources. Units are <math> \rm{ \mu K^2_{CMB}} </math>. |
| − | ==Production process== | + | ===Production process=== |
| − | Spectra are computed using cROMAster, a implementation of the pseudo-Cl method described in | + | Spectra are computed using cROMAster, a implementation of the pseudo-Cl method described in{{BibCite|master}}. In addition to the original approach, our implementation allows for estimation of cross-power spectra from two or more maps{{BibCite|polenta_CrossSpectra}}. The software package uses [http://healpix.sourceforge.net/ HEALPix] modules for spherical harmonic transform and Cl calculation. The schematic of the estimation process is as follows: |
* computing the a_lm coefficients from the input temperature map after masking Galactic Plane and point sources. | * computing the a_lm coefficients from the input temperature map after masking Galactic Plane and point sources. | ||
| Line 300: | Line 381: | ||
* estimating error bars on bandpowers from signal plus noise Monte Carlo simulations, where signal simulations include only CMB anisotropies. | * estimating error bars on bandpowers from signal plus noise Monte Carlo simulations, where signal simulations include only CMB anisotropies. | ||
| − | ==Inputs== | + | ===Inputs=== |
| − | |||
The inputs are the following: | The inputs are the following: | ||
| Line 324: | Line 404: | ||
* [[The RIMO#Beam_Window_Functions| Beam window functions]] | * [[The RIMO#Beam_Window_Functions| Beam window functions]] | ||
* Monte Carlo simulations | * Monte Carlo simulations | ||
| − | * binning scheme | + | * binning scheme [[Media:Power_spectra_CTP_bin_tt.pdf]]. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | ===File Names=== | ||
: {{PLASingleFile|fileType=cosmo|name=LFI_PowerSpect_030_R1.10.fits|link=LFI_PowerSpect_030_R1.10.fits}} | : {{PLASingleFile|fileType=cosmo|name=LFI_PowerSpect_030_R1.10.fits|link=LFI_PowerSpect_030_R1.10.fits}} | ||
: {{PLASingleFile|fileType=cosmo|name=LFI_PowerSpect_044_R1.10.fits|link=LFI_PowerSpect_044_R1.10.fits}} | : {{PLASingleFile|fileType=cosmo|name=LFI_PowerSpect_044_R1.10.fits|link=LFI_PowerSpect_044_R1.10.fits}} | ||
: {{PLASingleFile|fileType=cosmo|name=LFI_PowerSpect_070_R1.10.fits|link=LFI_PowerSpect_070_R1.10.fits}} | : {{PLASingleFile|fileType=cosmo|name=LFI_PowerSpect_070_R1.10.fits|link=LFI_PowerSpect_070_R1.10.fits}} | ||
| − | ==Meta Data == | + | ===Meta Data === |
| − | |||
The angular power spectra source list in each frequency is structured as a FITS binary table. | The angular power spectra source list in each frequency is structured as a FITS binary table. | ||
The Fits extension is composed by the columns described below: | The Fits extension is composed by the columns described below: | ||
| Line 666: | Line 545: | ||
</pre> | </pre> | ||
| − | = References = | + | == References == |
| − | < | + | <References /> |
| − | + | ||
| − | + | ||
| + | |||
| − | [[Category:Mission | + | [[Category:Mission products|006]] |
Latest revision as of 15:37, 18 July 2014
HFI maps power spectra[edit]
Angular power spectra of cut sky CMB dominated maps are provided to allow independent cosmological analysis at high .
Product description[edit]
The auto and cross-spectra of the 13 detector set (detset) maps at 100, 143 and 217 GHz, all analyzed on the same 42.8% of the sky, are provided. The mask used is apodized to reduce the power leakage from large scale to small scale (see input section). Except for the removal of the most contaminated pixels through masking, no attempt at astrophysical components separation has been performed.
For each pair of detectors and , are provided,
- the unbinned estimated power spectrum for all from 0 to 3508 (see Figure 1 below), as well as
- the unbinned symmetric covariance matrix
\begin{align}
\hat{M}^{XY}_{\ell \ell'} \equiv \langle\Delta \hat{C}^{XY}_\ell\Delta \hat{C}^{XY}_{\ell'}\rangle
\label{eq:covmatCl}
\end{align} for all on the same range. At the price of some extra hypotheses, that information can be used to build the likelihood of a given theoretical power spectrum given the data, and therefore determine the best cosmological models fitting the data. Several examples of such high- likelihoods are described, discussed and compared in Planck-2013-XV[1].
$ \newcommand{\bfE}{\boldsymbol{\mathrm{E}}} \newcommand{\bfM}{\boldsymbol{\mathrm{M}}} \newcommand{\bfx}{\boldsymbol{\mathrm{x}}} \newcommand{\lmax}{\ell_{\mathrm{max}}} $ Note that only describes the statistical covariance of the power spectrum induced by the signal and noise of the input map on the cut sky begin analyzed. Most sources of systematic effects (such as uncertainty on the beam modeling) as well as post-processing steps (such as foreground subtraction) will increase the covariance. In the particular case of the uncertainty on the beam window functions , the RIMO provides for each pair a set of eigen-vectors of the relative error on (see HFI time response and beams paper[2]), defined for in and in (with being 2500, 3000 or 4000 when the lowest of the nominal frequencies of the detectors and is respectively 100, 143 or 217GHz). The extra contribution to the covariance of is then \begin{align}
\hat{M}^{XY, \mathrm{beam}}_{\ell_1 \ell_2} = 4 \hat{C}^{XY}_{\ell_1} \hat{C}^{XY}_{\ell_2} \sum_{p=1}^{5} E^{XY}_p(\ell_1) E^{XY}_p(\ell_2).
\label{eq:covmatBeam}
\end{align}
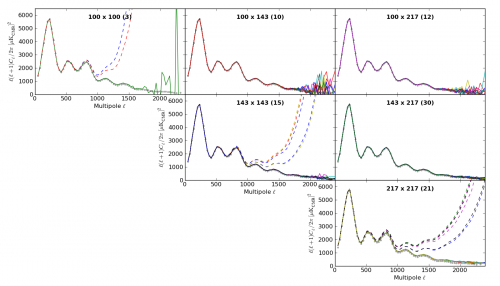
Auto and Cross Power Spectra[edit]
The spectra computed up to using PolSpice[3][4] are corrected from the effect of the cut sky, and from the nominal beam window function and average pixel function. The different steps of the calculation are
- computation of the Spherical Harmonics coefficients of the masked input maps and of the input mask ,
\begin{align}
\tilde{a}^X_{\ell m} = \sum_p \Omega_p\, \Delta T^X(p)\, w(p)\, Y^*_{\ell m}(p), \label{eq:almdef}
\end{align} \begin{align}
\tilde{w}^{(n)}_{\ell m} = \sum_p \Omega_p\ w^n(p)\, Y^*_{\ell m}(p); \label{eq:wlmdef}
\end{align} where the sum is done over all sky pixels , is the pixel area, and is either 1 or 2;
- the sky (cross or auto) pseudo-power spectrum and mask power spectrum are computed from the and ,
\begin{align}
\tilde{C}^{XY}_\ell = \sum_{\ell m} \tilde{a}^X_{ m} \tilde{a}^{Y^*}_{\ell m} / (2 \ell + 1), \label{eq:alm2cl}
\end{align} \begin{align}
\tilde{W}^{(n)}_\ell = \sum_{\ell m} \tilde{w}^{(n)}_{ m} {\tilde{w}^{(n)}}^*_{\ell m} / (2 \ell + 1); \label{eq:wlm2wl}
\end{align}
- the sky and mask angular correlation function are computed from the respective power spectra,
\begin{align}
\tilde{\xi}(\theta) = \sum_\ell \frac{2\ell+1}{4\pi} \tilde{C}_{\ell} P_\ell(\theta),\label{eq:cl2xi}
\end{align} \begin{align}
\tilde{\xi}_W(\theta) = \sum_\ell \frac{2\ell+1}{4\pi} \tilde{W}^{(1)}_{\ell} P_\ell(\theta),
\end{align} where is the Legendre Polynomial of order ;
- the ratio of the sky angular correlation by the mask correlation provides the cut sky corrected angular correlation,
\begin{align}
\xi(\theta) = \tilde{\xi}(\theta) / \tilde{\xi}_W(\theta); \label{eq:xi_deconv}
\end{align}
- the sky angular correlation function which is then turned into a angular power spectrum,
\begin{align}
{C'}_\ell = 2\pi \sum_i w_i \xi(\theta_i) P_\ell(\theta_i), \label{eq:xi2cl}
\end{align} where are the weights of the Gauss-Legendre quadrature, for in ;
- the resulting power spectrum is corrected from the nominal beam window function and average pixel window function , to provide the final Spice estimator ,
\begin{align}
\hat{C}_\ell = {C'}_\ell / \left( B^2_\ell w^2_{\mathrm{pix}}(\ell) \right). \label{eq:clfinal}
\end{align}
Covariance Matrices[edit]
The covariance matrix for the pair is computed by PolSpice using the formalism described in[5], also sketched in the appendix of CMB power spectra and likelihood paper[1], assuming the instrumental noise to be white and uniform.
$ \newcommand{\hC}{\hat C} $ One note that a good approximation of the covariance matrix of the pseudo is related to the underlying estimated auto- and cross-spectra through \begin{align} \tilde{M}_{\ell_1\ell_2} \equiv \langle\Delta \tilde{C}^{XY}_{\ell_1}\Delta \tilde{C}^{XY}_{\ell_2}\rangle = \left( \left(\hC^{XX}_{\ell_1} \hC^{YY}_{\ell_1} \hC^{XX}_{\ell_2} \hC^{YY}_{\ell_2}\right)^{1/2}
+ \hC^{XY}_{\ell_1} \hC^{XY}_{\ell_2} \right)
\sum_{\ell_3} \frac{2\ell_3+1}{4\pi} \tilde{W}^{(2)}_{\ell_3} \left(
\begin{array}{ccc}
\! \ell_1\! & \ell_2\! & \ell_3\! \\
\! 0 \! & 0 \! & 0 \!
\end{array}
\right)^2,
\label{eq:covpseudo} \end{align} where is the power spectrum of the square of the pixel mask (Eqs. \ref{eq:wlmdef} and \ref{eq:wlm2wl} for ). The covariance matrix of the Spice estimator is then computed by applying Eqs. \ref{eq:cl2xi}, \ref{eq:xi_deconv}, \ref{eq:xi2cl} and \ref{eq:clfinal} on each row and column of .
Inputs[edit]
- Maps
- The input maps are the 13 HFI detset (see Type of maps section for details) maps available at 100, 143 and 217 GHz. These are the same as the ones used for high-ell part of the likelihood code, but that code applies different masks for each cross-spectra in order to minimize further the foreground contamination.
- Sky mask
- All maps were analyzed on the 42.8% of the sky defined by the apodized mask HFI_PowerSpect_Mask_2048_R1.10.fits, which masks out Galactic Plane and point sources (see Planck-2013-XV[1]), and which is shown in Figure 2 below
- Beam Window Function
- The beam window functions , and their uncertainties, are the ones used in the high-ell likelihood analysis, described in section 6.1 "Error Eigenmodes" of Planck-2013-XV[1] and provided in the HFI RIMO.
Related products[edit]
None
FITS file structure[edit]
Power spectra are provided for the auto and cross products built from the 13 detsets available at 100, 143 and 217 GHz, namely:
- 100-ds1, 100-ds2,
- 143-ds1, 143-ds2, 143-5, 143-6, 143-7,
- 217-ds1, 217-ds2, 217-1, 217-2, 217-3, 217-4
which makes 13*(13+1)/2 = 91 spectra. Filenames for the auto spectra are HFI_PowerSPect_{detset}_Relnum.fits and HFI_PowerSPect_{detset1}x{detset2}_Relnum.fits for the auto- and cross-spectra, respectively. The list of the 91 files is given below. Each files contains 2 BINTABLE extensions:
| 1. EXTNAME = 'POW-SPEC' (BINTABLE) | |||
|---|---|---|---|
| Column Name | Data Type | Units | Description |
| TEMP_CL | Real*4 | Kcmb2 | the power spectrum |
| TEMP_CL_ERR | Real*4 | Kcmb2 | estimate of the uncertainty in the power spectrum |
| Keyword | Data Type | Value | Description |
| LMIN | Integer | 0 | First monopole |
| LMAX | Integer | value | Last monopole |
| 2. EXTNAME = 'PSCOVMAT' (IMAGE) | |||
| COVMAT | Real*4 | Kcmb4 | the covariance matrix |
| Keyword | Data Type | Value | Description |
| NAXIS1 | Integer | dim1 | matrix first dimension |
| NAXIS2 | Integer | dim2 | matrix second dimension |
where LMAX is the same for both vectors, and dim1 = dim2 = LMAX+1 by construction.
List of filenames[edit]
| Auto power spectra |
|---|
| HFI_PowerSpect_100-ds1_R1.10.fits |
| HFI_PowerSpect_100-ds2_R1.10.fits |
| HFI_PowerSpect_143-5_R1.10.fits |
| HFI_PowerSpect_143-6_R1.10.fits |
| HFI_PowerSpect_143-7_R1.10.fits |
| HFI_PowerSpect_143-ds1_R1.10.fits |
| HFI_PowerSpect_143-ds2_R1.10.fits |
| HFI_PowerSpect_217-1_R1.10.fits |
| HFI_PowerSpect_217-2_R1.10.fits |
| HFI_PowerSpect_217-3_R1.10.fits |
| HFI_PowerSpect_217-4_R1.10.fits |
| HFI_PowerSpect_217-ds1_R1.10.fits |
| HFI_PowerSpect_217-ds2_R1.10.fits |
| Cross power spectra |
| HFI_PowerSpect_100-ds1x100-ds2_R1.10.fits |
| HFI_PowerSpect_100-ds1x143-5_R1.10.fits |
| HFI_PowerSpect_100-ds1x143-6_R1.10.fits |
| HFI_PowerSpect_100-ds1x143-7_R1.10.fits |
| HFI_PowerSpect_100-ds1x143-ds1_R1.10.fits |
| HFI_PowerSpect_100-ds1x143-ds2_R1.10.fits |
| HFI_PowerSpect_100-ds1x217-1_R1.10.fits |
| HFI_PowerSpect_100-ds1x217-2_R1.10.fits |
| HFI_PowerSpect_100-ds1x217-3_R1.10.fits |
| HFI_PowerSpect_100-ds1x217-4_R1.10.fits |
| HFI_PowerSpect_100-ds1x217-ds1_R1.10.fits |
| HFI_PowerSpect_100-ds1x217-ds2_R1.10.fits |
| HFI_PowerSpect_100-ds2x143-5_R1.10.fits |
| HFI_PowerSpect_100-ds2x143-6_R1.10.fits |
| HFI_PowerSpect_100-ds2x143-7_R1.10.fits |
| HFI_PowerSpect_100-ds2x143-ds1_R1.10.fits |
| HFI_PowerSpect_100-ds2x143-ds2_R1.10.fits |
| HFI_PowerSpect_100-ds2x217-1_R1.10.fits |
| HFI_PowerSpect_100-ds2x217-2_R1.10.fits |
| HFI_PowerSpect_100-ds2x217-3_R1.10.fits |
| HFI_PowerSpect_100-ds2x217-4_R1.10.fits |
| HFI_PowerSpect_100-ds2x217-ds1_R1.10.fits |
| HFI_PowerSpect_100-ds2x217-ds2_R1.10.fits |
| HFI_PowerSpect_143-5x143-6_R1.10.fits |
| HFI_PowerSpect_143-5x143-7_R1.10.fits |
| HFI_PowerSpect_143-5x217-1_R1.10.fits |
| HFI_PowerSpect_143-5x217-2_R1.10.fits |
| HFI_PowerSpect_143-5x217-3_R1.10.fits |
| HFI_PowerSpect_143-5x217-4_R1.10.fits |
| HFI_PowerSpect_143-5x217-ds1_R1.10.fits |
| HFI_PowerSpect_143-5x217-ds2_R1.10.fits |
| HFI_PowerSpect_143-6x143-7_R1.10.fits |
| HFI_PowerSpect_143-6x217-1_R1.10.fits |
| HFI_PowerSpect_143-6x217-2_R1.10.fits |
| HFI_PowerSpect_143-6x217-3_R1.10.fits |
| HFI_PowerSpect_143-6x217-4_R1.10.fits |
| HFI_PowerSpect_143-6x217-ds1_R1.10.fits |
| HFI_PowerSpect_143-6x217-ds2_R1.10.fits |
| HFI_PowerSpect_143-7x217-1_R1.10.fits |
| HFI_PowerSpect_143-7x217-2_R1.10.fits |
| HFI_PowerSpect_143-7x217-3_R1.10.fits |
| HFI_PowerSpect_143-7x217-4_R1.10.fits |
| HFI_PowerSpect_143-7x217-ds1_R1.10.fits |
| HFI_PowerSpect_143-7x217-ds2_R1.10.fits |
| HFI_PowerSpect_143-ds1x143-5_R1.10.fits |
| HFI_PowerSpect_143-ds1x143-6_R1.10.fits |
| HFI_PowerSpect_143-ds1x143-7_R1.10.fits |
| HFI_PowerSpect_143-ds1x143-ds2_R1.10.fits |
| HFI_PowerSpect_143-ds1x217-1_R1.10.fits |
| HFI_PowerSpect_143-ds1x217-2_R1.10.fits |
| HFI_PowerSpect_143-ds1x217-3_R1.10.fits |
| HFI_PowerSpect_143-ds1x217-4_R1.10.fits |
| HFI_PowerSpect_143-ds1x217-ds1_R1.10.fits |
| HFI_PowerSpect_143-ds1x217-ds2_R1.10.fits |
| HFI_PowerSpect_143-ds2x143-5_R1.10.fits |
| HFI_PowerSpect_143-ds2x143-6_R1.10.fits |
| HFI_PowerSpect_143-ds2x143-7_R1.10.fits |
| HFI_PowerSpect_143-ds2x217-1_R1.10.fits |
| HFI_PowerSpect_143-ds2x217-2_R1.10.fits |
| HFI_PowerSpect_143-ds2x217-3_R1.10.fits |
| HFI_PowerSpect_143-ds2x217-4_R1.10.fits |
| HFI_PowerSpect_143-ds2x217-ds1_R1.10.fits |
| HFI_PowerSpect_143-ds2x217-ds2_R1.10.fits |
| HFI_PowerSpect_217-1x217-2_R1.10.fits |
| HFI_PowerSpect_217-1x217-3_R1.10.fits |
| HFI_PowerSpect_217-1x217-4_R1.10.fits |
| HFI_PowerSpect_217-1x217-ds1_R1.10.fits |
| HFI_PowerSpect_217-1x217-ds2_R1.10.fits |
| HFI_PowerSpect_217-2x217-3_R1.10.fits |
| HFI_PowerSpect_217-2x217-4_R1.10.fits |
| HFI_PowerSpect_217-2x217-ds1_R1.10.fits |
| HFI_PowerSpect_217-2x217-ds2_R1.10.fits |
| HFI_PowerSpect_217-3x217-4_R1.10.fits |
| HFI_PowerSpect_217-3x217-ds1_R1.10.fits |
| HFI_PowerSpect_217-3x217-ds2_R1.10.fits |
| HFI_PowerSpect_217-4x217-ds1_R1.10.fits |
| HFI_PowerSpect_217-4x217-ds2_R1.10.fits |
| HFI_PowerSpect_217-ds1x217-ds2_R1.10.fits |
| Sky mask |
| HFI_PowerSpect_Mask_2048_R1.10.fits |
The full list of HFI power spectra with links to the files in the PLA can be found here.
LFI maps power spectra[edit]
Product description[edit]
The angular power spectrum provides information about the distribution of power on the sky map at the various angular scales. It is especially important for CMB, because it is characterized by a number of features, most notably the acoustic peaks, that encode the dependence from cosmological parameters. Therefore, angular power spectra are the basic inputs for the Planck Likelihood Code, and for estimation of cosmological parameters in general.
For this release we have computed only temperature power spectra. Polarization is not included.
Please note that these spectra come from frequency maps. No component separation has been applied, and we have only masked Galactic Plane and detected point sources. Units are .
Production process[edit]
Spectra are computed using cROMAster, a implementation of the pseudo-Cl method described in[6]. In addition to the original approach, our implementation allows for estimation of cross-power spectra from two or more maps[7]. The software package uses HEALPix modules for spherical harmonic transform and Cl calculation. The schematic of the estimation process is as follows:
- computing the a_lm coefficients from the input temperature map after masking Galactic Plane and point sources.
- computing the pseudo power spectrum from the alms.
- estimating the bias due to the noise power spectrum of the map from noise-only Monte Carlo simulations based on detector noise properties
- correcting for the effect of the adopted mask by computing the mode-mode coupling kernel corresponding to that mask
- deconvolving the effect due to the finite angular resolution of the telescope by using the beam window function
- deconvolving the effect due to the finite size of the pixel in the map by using a pixel window function
- binning the power spectrum from individual multipoles into bandpowers
- estimating error bars on bandpowers from signal plus noise Monte Carlo simulations, where signal simulations include only CMB anisotropies.
Inputs[edit]
The inputs are the following:
- LFI Frequency Maps
- Point source and galactic plane masks (the name being specified in the comment keyword in the header, see Note in Meta Data section below):
| Point source masks | |||
|---|---|---|---|
| LFI_MASK_030-ps_2048_R1.00.fits | |||
| LFI_MASK_044-ps_2048_R1.00.fits | |||
| LFI_MASK_070-ps_2048_R1.00.fits | |||
| Galactic plane masks | |||
| COM_MASK_gal-06_2048_R1.00.fits | |||
| COM_MASK_gal-07_2048_R1.00.fits | |||
- Beam window functions
- Monte Carlo simulations
- binning scheme Media:Power_spectra_CTP_bin_tt.pdf.
File Names[edit]
Meta Data[edit]
The angular power spectra source list in each frequency is structured as a FITS binary table. The Fits extension is composed by the columns described below:
| Column Name | Data Type | Units | Description |
|---|---|---|---|
| L | Integer*4 | ell parameter | |
| TEMP_CL | Real*8 | uK | (temperature) |
| TEMP_CL_ERR | Real*8 | uK | error |
Note.- in the comment keyword in the header, the galactic and point source maps used to generate the angular spectra are specified (LFI_MASK_030-ps_2048_R1.00.fits and COM_MASK_gal-06_2048_R1.00.fits in the example below). Note also that, due to an oversight, the mask description related to COM_MASK_gal-xxx is wrong and should refer to the galactic mask.
Below an example of the header.
XTENSION= 'BINTABLE' /Written by IDL: Sat Feb 16 00:44:22 2013 BITPIX = 8 / NAXIS = 2 /Binary table NAXIS1 = 20 /Number of bytes per row NAXIS2 = 130 /Number of rows PCOUNT = 0 /Random parameter count GCOUNT = 1 /Group count TFIELDS = 3 /Number of columns TFORM1 = '1J ' /Integer*4 (long integer) TTYPE1 = 'L ' / TFORM2 = '1D ' /Real*8 (double precision) TTYPE2 = 'TEMP_CL ' / TFORM3 = '1D ' /Real*8 (double precision) TTYPE3 = 'TEMP_CL_ERR' / EXTNAME = 'POW-SPEC' / Extension name EXTVER = 1 /Extension version DATE = '2013-02-15' /Creation date TUNIT2 = 'uK_CMB^2' / TUNIT3 = 'uK_CMB^2' / FILENAME= 'LFI_PowerSpect_030_R1.00.fits' / PROCVER = 'Dx9_delta' / COMMENT --------------------------------------------- COMMENT Original Inputs COMMENT --------------------------------------------- COMMENT TT_30GHz_maskCS0.60_PS30GHzdet_febecopWls COMMENT Used Point source Mask LFI_MASK_030-ps_2048_R1.00.fits COMMENT Used Point source Mask COM_MASK_gal-06_2048_R1.00.fits COMMENT Used FebeCoP 30 GHz wls END
Below an example of the header of two masks used as input: COM_MASK_gal-06_2048_R1.00.fits and LFI_MASK_030-ps_2048_R1.00.fits:
XTENSION= 'BINTABLE' / binary table extension BITPIX = 8 / 8-bit bytes NAXIS = 2 / 2-dimensional binary table NAXIS1 = 4 / width of table in bytes NAXIS2 = 50331648 / number of rows in table PCOUNT = 0 / size of special data area GCOUNT = 1 / one data group (required keyword) TFIELDS = 1 / number of fields in each row TTYPE1 = 'Mask ' / label for field 1 TFORM1 = 'E ' / data format of field: 4-byte REAL TUNIT1 = 'none ' / physical unit of field EXTNAME = '06-GalMask' DATE = '2013-02-16T11:07:42' / file creation date (YYYY-MM-DDThh:mm:ss UT) CHECKSUM= 'NaGVNZGUNaGUNYGU' / HDU checksum updated 2013-02-16T11:07:43 DATASUM = '2540860986' / data unit checksum updated 2013-02-16T11:07:43 COMMENT COMMENT *** Planck params *** COMMENT PIXTYPE = 'HEALPIX ' / HEALPIX pixelisation ORDERING= 'NESTED ' / Pixel ordering scheme, either RING or NESTED NSIDE = 2048 / Resolution parameter for HEALPIX FIRSTPIX= 0 / First pixel # (0 based) LASTPIX = 50331647 / Last pixel # (0 based) INDXSCHM= 'IMPLICIT' / Indexing: IMPLICIT or EXPLICIT OBJECT = 'FULLSKY ' / Sky coverage, either FULLSKY or PARTIAL BAD_DATA= -1.6375E+30 COORDSYS= 'GALACTIC' FILENAME= 'COM_MASK_gal-06_2048_R1.00.fits' COMMENT --------------------------------------------------------------------- COMMENT Combined galactic mask 0.6 sky fraction COMMENT Objects used: COMMENT /sci_planck/lfi_dpc_test/ashdown/repository/masks/component_separation/d COMMENT x9/combined_mask_0.60_sky_fraction.fits COMMENT --------------------------------------------------------------------- END
XTENSION= 'BINTABLE' / binary table extension BITPIX = 8 / 8-bit bytes NAXIS = 2 / 2-dimensional binary table NAXIS1 = 4 / width of table in bytes NAXIS2 = 50331648 / number of rows in table PCOUNT = 0 / size of special data area GCOUNT = 1 / one data group (required keyword) TFIELDS = 1 / number of fields in each row TTYPE1 = 'Mask ' / label for field 1 TFORM1 = 'E ' / data format of field: 4-byte REAL TUNIT1 = 'none ' / physical unit of field EXTNAME = '030-PSMask' DATE = '2013-02-16T11:03:20' / file creation date (YYYY-MM-DDThh:mm:ss UT) CHECKSUM= 'fR7ThO7RfO7RfO7R' / HDU checksum updated 2013-02-16T11:03:21 DATASUM = '3828742620' / data unit checksum updated 2013-02-16T11:03:21 COMMENT COMMENT *** Planck params *** COMMENT PIXTYPE = 'HEALPIX ' / HEALPIX pixelisation ORDERING= 'NESTED ' / Pixel ordering scheme, either RING or NESTED NSIDE = 2048 / Resolution parameter for HEALPIX FIRSTPIX= 0 / First pixel # (0 based) LASTPIX = 50331647 / Last pixel # (0 based) INDXSCHM= 'IMPLICIT' / Indexing: IMPLICIT or EXPLICIT OBJECT = 'FULLSKY ' / Sky coverage, either FULLSKY or PARTIAL BAD_DATA= -1.6375E+30 COORDSYS= 'GALACTIC' FILENAME= 'LFI_MASK_030-ps_2048_R1.00.fits' COMMENT --------------------------------------------------------------------- COMMENT The radius of the holes is 3 times the sigma of the beam at the correspo COMMENT nding frequency and sigma is FWHM/(2*sqrt(2ln2)) COMMENT FWHM at 30GHz used = 33.158 arcmin COMMENT Objects used: COMMENT /planck/sci_ops1/LFI_MAPs/DX9_Delta/MASKs/mask_ps_30GHz_beam33amin_nside COMMENT 2048.00_DX9_nonblind_holesize3.fits COMMENT --------------------------------------------------------------------- END
References[edit]
- ↑ 1.01.11.21.3 Planck 2013 results. XV. CMB power spectra and likelihood, Planck Collaboration, 2014, A&A, 571, A15.
- ↑ Planck 2013 results. VII. HFI time response and beams, Planck Collaboration, 2014, A&A, 571, A7.
- ↑ Fast Cosmic Microwave Background Analyses via Correlation Functions, I. Szapudi, S. Prunet, D. Pogosyan, A. S. Szalay, J. R. Bond, ApJS, 548, L115-L118, (2001).
- ↑ Fast estimation of polarization power spectra using correlation functions, G. Chon, A. Challinor, S. Prunet, E. Hivon, I. Szapudi, MNRAS, 350, 914-926, (2004).
- ↑ Myths and truths concerning estimation of power spectra: the case for a hybrid estimator, G. Efstathiou, MNRAS, 349, 603-626, (2004).
- ↑ MASTER of the Cosmic Microwave Background Anisotropy Power Spectrum: A Fast Method for Statistical Analysis of Large and Complex Cosmic Microwave Background Data Sets, E. Hivon, K. M. Górski, C. B. Netterfield, B. P. Crill, S. Prunet, F. Hansen, ApJ, 567, 2-17, (2002).
- ↑ Unbiased estimation of an angular power spectrum, G. Polenta, D. Marinucci, A. Balbi, P. de Bernardis, E. Hivon, S. Masi, P. Natoli, N. Vittorio, J. Cosmology Astropart. Phys., 11, 1, (2005).
(Planck) High Frequency Instrument
Cosmic Microwave background
Flexible Image Transfer Specification
Planck Legacy Archive
(Planck) Low Frequency Instrument
Full-Width-at-Half-Maximum
