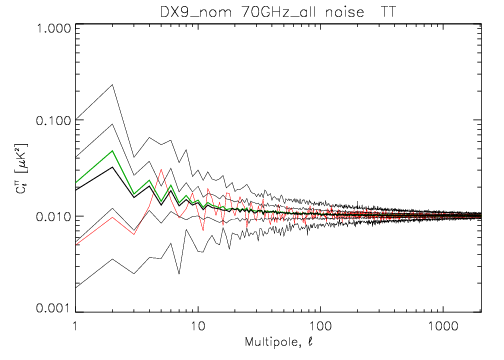Difference between revisions of "Map-making LFI"
| Line 24: | Line 24: | ||
When the noise MC for the first Planck data release was performed, calibrated data for five sky surveys were available. In addition to frequency maps for the nominal survey and the full survey (all five sky surveys), single-survey and 70 GHz horn-pair maps were produced in the noise MC, resulting in 27 different cases of LFI maps, a subset of the map cases produced from the flight data. For each case $102--1026$ realizations were produced. | When the noise MC for the first Planck data release was performed, calibrated data for five sky surveys were available. In addition to frequency maps for the nominal survey and the full survey (all five sky surveys), single-survey and 70 GHz horn-pair maps were produced in the noise MC, resulting in 27 different cases of LFI maps, a subset of the map cases produced from the flight data. For each case $102--1026$ realizations were produced. | ||
| − | here's | + | ===Example== |
| + | |||
| + | here's two figures | ||
[[File:LFI_4_5_5_4_cl_TT_stat_noisemc_101_1sec_70GHz_all_DX9_nom.png]] | [[File:LFI_4_5_5_4_cl_TT_stat_noisemc_101_1sec_70GHz_all_DX9_nom.png]] | ||
| + | |||
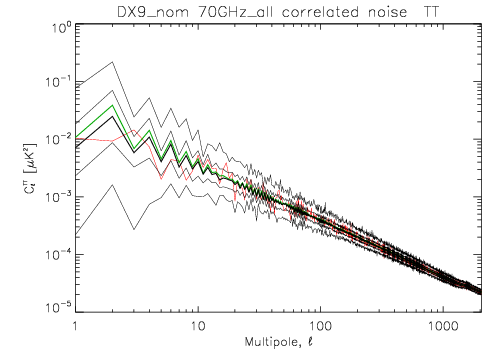
| + | [[File:LFI_4_5_5_4_cl_TT_stat_rcnoisemc_101_1sec_70GHz_all_DX9_nom.png]] | ||
Revision as of 12:05, 19 October 2012
Noise Monte Carlo Simulation[edit]
Overview[edit]
Calculating and handling full pixel-to-pixel noise covariances in Planck maps if feasible only at low resolution. To support the analysis of high-resolution maps, a Monte Carlo set of noise maps were produced. These maps were produced from noise timelines using the same map-making procedure as for the flight data. Such noise Monte Carlos were produced at two levels of the analysis: 1) LFI Monte Carlo (MC) as part of the LFI data processing, and 2) Full Focal Plane (FFP) Monte Carlo as part of the joint HFI/LFI data processing. This page describes the LFI noise MC. For the FFP MC, see HL-sims.
Inputs[edit]
The noise MC uses a three-parameter (white noise level ($\sigma$), slope, and knee frequency ($f_\mathrm{knee}$)) noise model, where the noise consists of white noise and correlated ($1/f$) noise and the latter has a power spectrum
- $ P(f) = \frac{2\sigma^2}{f_\mathrm{sample}}\left(\frac{f}{f_\mathrm{knee}}\right)^\mathrm{slope} $.
Here $f_\mathrm{sample}$ is the sampling frequency of the instrument. The noise parameters were determined separately for each radiometer as described in TOI-Noise LFI, assuming they stayed constant over the mission.
The detector pointing was reconstructed from satellite pointing, focal-plane geometry, pointing correction (tilt angle), and sample timing, using Level-S simulation software. The same pointing solution (two focal planes) was used as for the LFI flight maps. Due to numerical accuracy, the detector pointing in the noise MC was not exactly the same as for the flight maps, but some data samples (of the order of one in a thousand) whose pointing was near the pixel boundary ended up assigned to the neighboring pixel. During the map-making from the flight data, a gap file was produced to represent the samples that were omitted from map-making due to various flags. This gap files was used in the noise MC instead of the full set of flags. The flight map-making used a destriping mask to exclude regions of strong signal gradients from contributing to the noise baseline solution. These same destriping masks (one for each frequency channel) were used for the noise MC.
Production[edit]
The noise was generated internally in the Madam map-making code using a Stochastic Differential Equation (SDE) method, to avoid time-consuming writing and reading noise timelines to/from disk. Noise for each pointing period was generated separately, using a double-precision random number seed constructed from the realization number, radiometer number, and the pointing period number; to allow regeneration of the same noise realization when needed. White noise and $1/f$ noise were generated separately.
The same map-making code (Madam) with the same parameter settings was used for the noise MC as for the flight maps. In addition to the destriped maps from the full noise (output maps), also binned maps from just the white noise (binned white noise maps) were produced; they represent the white noise part of the output maps. The difference between these two maps represent the residual correlated noise in the output map. The maps were made at Healpix resolution $N_\mathrm{side} = 1024$. For low-resolution analysis, these maps were downgraded (and the temperature part was smoothed) to $N_\mathrm{side} = 32$ and $N_\mathrm{side} = 16$.
When the noise MC for the first Planck data release was performed, calibrated data for five sky surveys were available. In addition to frequency maps for the nominal survey and the full survey (all five sky surveys), single-survey and 70 GHz horn-pair maps were produced in the noise MC, resulting in 27 different cases of LFI maps, a subset of the map cases produced from the flight data. For each case $102--1026$ realizations were produced.
=Example[edit]
here's two figures
(Planck) Low Frequency Instrument
(Planck) High Frequency Instrument