Difference between revisions of "Beams LFI"
(→Main Beams and Focal Plane calibration) |
(→Scanning beam:) |
||
| (124 intermediate revisions by 7 users not shown) | |||
| Line 2: | Line 2: | ||
== Overview == | == Overview == | ||
| − | |||
| − | LFI | + | LFI observed the sky with 11 pairs of beams associated with the 22 pseudo-correlation radiometers. |
| − | Each beam of the radiometer pair (Radiometer Chain Assembly - RCA) is | + | Each beam of the radiometer pair (Radiometer Chain Assembly - RCA) is labelled as LFIXXM or LFIXXS. Here "XX" is the RCA number ranging from 18 to 28, while "M" and "S" are the two polarizations, namely the main-arm and side-arm of the orthomode transducers {{BibCite|darcangelo2009b}} (see also [[LFI design, qualification, and performance#Naming Convention|LFI naming convention]]). |
| − | |||
| − | |||
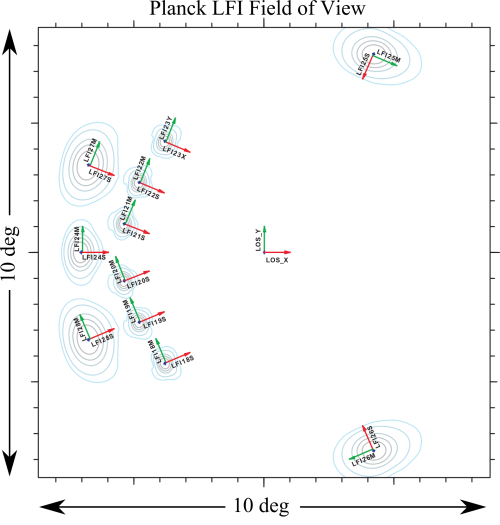
| + | [[File:fieldofview.png|500px|thumb|centre|'''Figure 1. A sketch of the Planck LFI field of view in the (<i>u</i>,<i>v</i>) plane is shown. The polarizations direction on the sky are highlighted by the coloured arrows. The M-polarization is shown in green and the S-polarization in red. Main beam shapes are shown for completeness and they are not representative of flight beams.''']] | ||
| + | Details are given in {{PlanckPapers|planck2014-a05}}. Please note that many figures below refer to the Planck release {{PlanckPapers|planck2013-p02d}}, since they have not changed significantly. | ||
<!-- | <!-- | ||
| Line 16: | Line 15: | ||
| − | ; main beam: is the portion of the pattern that extends up to 1.9, 1.3, and 0.9 degrees from the beam center at 30, 44, and 70 GHz, respectively. | + | ; the main beam: is the portion of the beam pattern that extends up to 1.9, 1.3, and 0.9 degrees from the beam center at 30, 44, and 70 GHz, respectively. |
| − | ; near sidelobes: is the pattern contained between the main beam angular limit and 5 degrees from the beam center (this is often called <b>intermediate beam</b>). | + | ; near sidelobes: is the pattern contained between the main beam angular limit and 5 degrees from the beam center (this is often called the <b>intermediate beam</b>). |
| − | ; far sidelobes: is the pattern at angular | + | ; far sidelobes: is the pattern at angular distance more than 5 degrees from the beam center. |
--> | --> | ||
| − | == | + | == Beam normalization == |
| − | + | Following the same procedure applyed during the 2015 release {{PlanckPapers|planck2014-a05}} we didn't normalize the beam since up to 1% of the solid angle of the LFI beams falls into the sidelobes, unevenly distributed and concentrated mainly in two areas, namely the main part and sub-spillover. | |
| − | + | We employ full 4π beams. Important to note is that roughly 1% of the signal found in the sidelobes is missing from the vicinity of the main beam, so the main beam efficiency η ≈ 99%, which must be accounted for in any analysis of the maps. In particular, the window function used to correct the power spectra extracted from the maps allows for this efficiency. | |
| − | |||
| − | + | Details are given in {{PlanckPapers|planck2014-a05}}. | |
| − | + | == Polarized scanning beams and focal plane calibration == | |
| − | + | Focal plane calibration is based on the determination of the beam pointing parameters in the nominal line of sight (LOS) frame derived from measurements during Jupiter transits. The parameters that characterize the beam pointing are: | |
| + | |||
| + | * THETA_UV (θ<sub>uv</sub>); | ||
| + | * PHI_UV (φ<sub>uv</sub>). | ||
| + | |||
| + | They are calculated starting from <i>u</i>,<i>v</i> coordinates derived form the beam reconstruction algorithm: | ||
| + | |||
| + | <math>\theta_{uv} = \arcsin(u^2+v^2)</math>; | ||
| + | |||
| + | <math>\phi_{uv} = \arctan(v/u)</math>. | ||
Two additional angles are used to characterize the beams in the RIMO: | Two additional angles are used to characterize the beams in the RIMO: | ||
| − | * PSI_UV ( | + | * PSI_UV (ψ<sub>uv</sub>); |
| − | * PSI_POL ( | + | * PSI_POL (ψ<sub>pol</sub>). |
| − | + | The angles ψ<sub>uv</sub> and ψ<sub>pol</sub> are <i>not</i> derived from measurements, but rather are estimated from optical simulations. They are the quantities that represent the polarization direction of each beam, assuming that the M- and S-beams of the same RCA point at the same direction on the sky. | |
| − | The | + | The polarized scanning beams were evaluated from optical simulations using the GRASP physical optics code, by appropriately tuning the Radio Frequency Flight Model (RFFM, {{PlanckPapers|tauber2010b}}). |
| − | + | The Radio Frequency Tuned Model (RFTM) was implemented to fit the in-flight beam measurements with an electromagnetic model. The LFI main beams can be considered linearly polarized, but the non-null cross-polarization has an impact on the polarization measurements. Since we are not able to measure the cross-polar beam in flight, we have relied on simulations validated by accurate beam measurements. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The model beams were monochromatic and were computed at various frequencies across a 6-GHz band around the optical centre frequency (OCF) with non-uniform steps (denser sampling where the bandpass was higher). For the RFTM model the OCFs were set at 28.0, 44.0, and 70.0 GHz. | |
| − | + | ||
| − | + | For each simulated beam we created a map of the Stokes polarization parameters. On those maps we performed a weighted in-band average to recover our best estimation of the polarized beam shape. The weighting function was the [[The_RIMO#LFI_2|RIMO]] transmission function. | |
| − | + | ||
| − | + | The delivered [[Scanning_Beams|products]] includes the in-band averaged Stokes parameter scanning maps of main beams, intermediate beams, and sidelobes. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
== Effective beams == | == Effective beams == | ||
| − | |||
| − | The ' | + | The 2018 effective beam estimation procedure didn't change with respect 2015 release, new summary values are perfectly in line with the once obtained in the 2015, see {{PlanckPapers|planck2016-l02}}. |
| − | It captures the complete information about the difference between the true and observed | + | The "effective beam" is the average of all scanning beams pointing at a certain direction within a given pixel of the sky map for a given scan strategy. It takes into account the coupling between azimuthal asymmetry of the beam and the uneven distribution of scanning angles across the sky. |
| + | It captures the complete information about the difference between the true and observed images of the sky. These beams are, by definition, the objects whose convolution with the true CMB sky produces the observed sky map. | ||
| − | The full algebra involving the effective beams for temperature and polarisation was presented in | + | The full algebra involving the effective beams for temperature and polarisation was presented in {{BibCite|mitra2010}}. Here we summarise the main results. The observed temperature on the sky <math>\widetilde{\mathbf{T}} </math> is a convolution of the true sky <math>\mathbf{T} </math> and the effective beam <math>\mathbf{B}</math>: |
<math> | <math> | ||
| − | \widetilde{\mathbf{T}} \ = \ \Delta\Omega \, \mathbf{B} \ | + | \widetilde{\mathbf{T}} \ = \ \Delta\Omega \, \mathbf{B} \ast \mathbf{T}, |
\label{eq:a0} | \label{eq:a0} | ||
</math> | </math> | ||
| Line 76: | Line 74: | ||
<math> | <math> | ||
| − | B_{ij} \ = \ | + | B_{ij} \ = \frac{\sum_t A_{ti} \, b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t)} {\sum_t A_{ti}}. |
\label{eq:EBT2} | \label{eq:EBT2} | ||
</math> | </math> | ||
| − | < | + | Here <i>t</i> labels the time samples, <i>A<sub>ti</sub></i> is 1 if the pointing direction falls in pixel number <i>i</i>, else it is 0, <math>\hat{\mathbf{p}}_t</math> represents the exact pointing direction (not approximated by the pixel centre location), and <math>\hat{\mathbf{r}}_j</math> is the centre of the pixel number <i>j</i>, where the scanning beam <math>b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t)</math> is being evaluated (if the pointing direction falls within the cut-off radius of 2.5×FWHM). |
| − | The algebra is a bit more involved for | + | The algebra is a bit more involved for polarized detectors. The observed stokes parameters at pixel <math>i</math>, <math>(\widetilde{I}, \widetilde{Q}, \widetilde{U})_i</math>, are related to the true Stokes parameters <math>(I, Q, U)_i</math>, by the following relation: |
<math> | <math> | ||
| − | ( \widetilde{I} \quad \widetilde{Q} \quad \widetilde{U})_i^T \ = \ \Delta\Omega \sum_j | + | ( \widetilde{I} \quad \widetilde{Q} \quad \widetilde{U})_i^{\rm T} \ = \ \Delta\Omega \sum_j B_{ij} \ast (I \quad Q \quad U)_j^{\rm T}, |
\label{eq:a1} | \label{eq:a1} | ||
</math> | </math> | ||
| − | where the | + | where the polarized effective beam matrix |
<math> | <math> | ||
| − | + | B_{ij} \ = \ \left[ \sum_t A_{tp} \mathbf{w}_t \mathbf{w}^{\rm T}_t \right]^{-1} \sum_t A_{ti} \, b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) \, \mathbf{w}_t \mathbf{W}^{\rm T}(\hat{\mathbf{r}}_j,\hat{\mathbf{p}}_t) \, , | |
\label{eq:a2} | \label{eq:a2} | ||
</math> | </math> | ||
| − | and <math>\mathbf{w}_t </math>and <math>\mathbf{W}(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) </math> are the the | + | and <math>\mathbf{w}_t </math>and <math>\mathbf{W}(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) </math> are the the polarization weight vectors, as defined in Mitra et al. (2010).{{BibCite|mitra2010}} |
| − | |||
| − | |||
| + | The task is to compute <math>B_{ij}</math> for temperature-only beams and the 3 × 3 matrices <math>\mathbf{B}_{ij}</math> for each pixel <i>i</i>, at every neighbouring pixel <i>j</i> that falls within the cut-off radius around the the centre of the <i>i</i>th pixel. | ||
| + | The effective beam is computed by stacking within a small field around each pixel of the HEALPix sky map. Due to the particular features of the Planck scanning strategy, coupled to the beam asymmetries in the focal plane, and data processing of the bolometer and radiometer TOIs, the resulting Planck effective beams vary over the sky. | ||
| − | + | FEBeCoP, given information on Planck scanning beams and detector pointing during a particular period, provides the pixelized cut-outs of both the effective beam (EB) and the point spread function (PSF), at all pixel-centre positions of the HEALPix-formatted map. | |
| − | |||
| − | FEBeCoP, given information on Planck scanning beams and detector pointing during a | ||
===Production process=== | ===Production process=== | ||
| − | |||
The methodology for computing effective beams for a scanning CMB experiment like Planck | The methodology for computing effective beams for a scanning CMB experiment like Planck | ||
| − | was presented in | + | was presented in Mitra et al. (2010).{{BibCite|mitra2010}} |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | FEBeCoP, or the Fast Effective Beam Convolution in Pixel space, is an approach for representing and computing effective beams (including both intrinsic beam shapes and the effects of scanning) that consists of the following steps: | ||
| + | * identify the individual detectors' instantaneous optical response function (presently we use elliptical Gaussian fits of Planck beams from observations of planets, but eventually, an arbitrary mathematical representation of the beam can be used on input); | ||
| + | * follow exactly the Planck scanning, and project the intrinsic beam on the sky at each actual sampling position; | ||
| + | * project instantaneous beams onto the pixelized map over a small region (typically <2.5 FWHM diameter); | ||
| + | * add up all beams that cross the same pixel and its vicinity during the period of interest; | ||
| + | * create a data object of all beams pointed at all <i>N</i><sub>pix</sub> directions of pixels in the map at the same resolution for which this precomputation was executed (dimension <i>N</i><sub>pix</sub> × a few hundred); | ||
| + | * use the resulting beam object for very fast convolution of all sky signals with the effective optical response of the observing mission. | ||
| − | Computation of the effective beams at each pixel for every detector is a challenging task for high resolution experiments. FEBeCoP is an efficient algorithm | + | Computation of the effective beams at each pixel for every detector is a challenging task for high resolution experiments. FEBeCoP is an efficient algorithm the implementation of which enabled us to compute the pixel-based effective beams using moderate computational resources. The algorithm uses different mathematical and computational techniques to bring down the computation cost to a practical level. That allowed several estimations of the effective beams for all Planck detectors for different scan and beam models as well as data sets of different length. |
| − | ====Pixel | + | ====Pixel-ordered detector angles==== |
| − | The main challenge in computing the effective beams is to go through the trillion samples, which | + | The main challenge in computing the effective beams is to go through the trillion samples, which becomes severely limited by I/O. In the first stage, for a given data set, ordered lists of pointing angles are made for each pixel – the Pixel-Ordered Detector Angles (PODA). This is an one-time process for each dataset. We used computers with large memory and used careful memory management bookkeeping to make this step efficient. |
====effBeam==== | ====effBeam==== | ||
| − | The effBeam part makes use of the precomputed PODA and unsynchronized reading from the disk to compute the beam. Here we tried to made sure that no repetition occurs in evaluating a trigonometric quantity. | + | The "effBeam" part makes use of the precomputed PODA and unsynchronized reading from the disk to compute the beam. Here we tried to made sure that no repetition occurs in evaluating a trigonometric quantity. |
| − | |||
| − | One important reason for separating the two steps is that they use different schemes | + | One important reason for separating the two steps is that they use different schemes for parallel computing. The PODA part requires parallelization over time-ordered data samples, while the effBeam part requires distribution of pixels among different computers. |
| − | ====Computational | + | ====Computational cost==== |
| − | The whole computation of the effective beams has been performed at the NERSC Supercomputing Center. In the table below | + | The whole computation of the effective beams has been performed at the NERSC Supercomputing Center. In the table below we display the computation cost at NERSC for the nominal mission both in terms of CPU hours and in human time. |
{|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | {|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
| − | |+ Computational cost for PODA, | + | |+ <small>'''Computational cost for PODA, effective beam and single map convolution. The cost in human time is computed using an arbitrary number of nodes/cores on the Carver or Hopper NERSC supercomputers.'''</small> |
|- | |- | ||
|Channel ||030 || 044 || 070 | |Channel ||030 || 044 || 070 | ||
|- | |- | ||
| − | |PODA/Detector | + | |PODA/Detector computation time (CPU hours) || 85 || 100 || 250 |
|- | |- | ||
| − | |PODA/Detector | + | |PODA/Detector computation time (human minutes) || 7 || 10 || 20 |
|- | |- | ||
| − | |Beam/Channel | + | |Beam/Channel computation time (CPU hours) || 900 || 2000 || 2300 |
|- | |- | ||
| − | |Beam/Channel | + | |Beam/Channel computation time (human hours) || 0.5 || 0.8 || 1 |
|- | |- | ||
| − | |Convolution | + | |Convolution computation time (CPU hours) || 1 || 1.2 || 1.3 |
|- | |- | ||
| − | |Convolution | + | |Convolution computation time (human seconds) || 1 || 1 || 1 |
|- | |- | ||
| − | |Effective | + | |Effective beam size (GB) || 173 || 123 || 28 |
|} | |} | ||
| − | + | The computation cost, especially for PODA and convolution, is heavily limited by the I/O capacity of the disk and so it depends on the overall usage of the cluster. | |
| − | The computation cost, especially for PODA and | ||
| − | |||
| − | |||
===Inputs=== | ===Inputs=== | ||
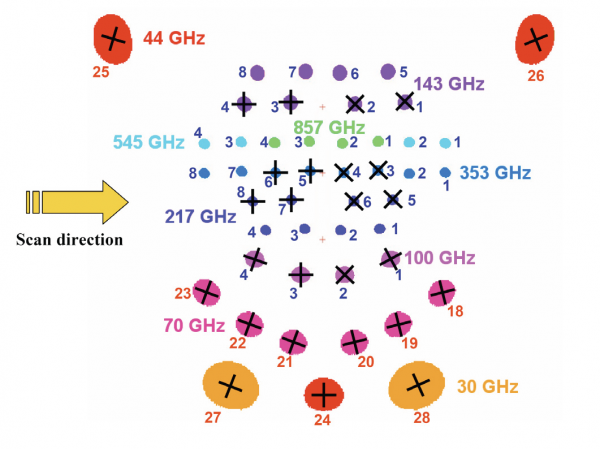
| − | In order to fix the convention | + | In order to fix the convention for presentation of the scanning and effective beams, we show the classic view of the Planck focal plane as seen by the incoming CMB photons. The scan direction is marked, and the direction toward the centre of the focal plane is at 85° with respect to the spin axis, pointing upward in the picture. |
| − | [[File:PlanckFocalPlane.png | 600px| thumb | center|'''Planck Focal Plane''']] | + | [[File:PlanckFocalPlane.png | 600px| thumb | center|'''Planck Focal Plane.''']] |
| − | ==== | + | ====Focal plane database:==== |
| − | The FPDB contains information on each detector, e.g., the orientation of the | + | The Focal Plane DataBase (FPDB) contains information on each detector, e.g., the orientation of the polarization axis, different weight factors, etc. See the instrument [[The RIMO|RIMOs]]: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | The scanning strategy | + | ====The scanning strategy:==== |
| − | + | The scanning strategy, specifically includes the three pointing angles for each detector for each sample. Detector pointings for the nominal mission cover about 15 months of observation from Operational Day (OD) 91 to OD 563 covering 3½ surveys. | |
| − | + | ====Scanning beam:==== | |
| − | + | The "scanning beam" was modelled for each detector using observations of planets. This was assumed to be constant over the whole mission, although FEBeCoP could be used for a few sets of scanning beams. | |
| − | ( | + | * LFI: [[Beams LFI#Main beams and Focalplane calibration|GRASP scanning beam]] - the scanning beams used are based on the Radio Frequency Tuned Model (RFTM) smeared to simulate the in-flight optical response. A description of the GRASP beams file formar (.grd) can be found in the "Technical Note PL-LFI-PST-TN-044: LFI Beams Delivery: Format Specifications": [[File: PST-TN-044_1-0.pdf|'''PST-TN-044_1-0.pdf''']]. |
| − | + | See the instrument [[The RIMO|RIMOs]]: | |
| + | {{PLASingleFile|fileType=rimo|name=LFI_RIMO_R1.12.fits|link=The LFI RIMO}}. | ||
| − | ====Beam cutoff radii==== | + | ====Beam cutoff radii:==== |
| − | * N times the geometric mean of FWHM of all detectors in a channel, where N=2.5 for all LFI frequency channels. | + | * <i>N</i> times the geometric mean of the FWHM values of all detectors in a channel, where <i>N</i>=2.5 for all LFI frequency channels. |
<!-- | <!-- | ||
{|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | {|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
|+'''Beam cut off radius''' | |+'''Beam cut off radius''' | ||
| − | | '''channel''' || '''Cutoff Radii in units of | + | | '''channel''' || '''Cutoff Radii in units of FWHM.''' || |
|- | |- | ||
|30 - 44 - 70 || 2.5 || | |30 - 44 - 70 || 2.5 || | ||
| Line 208: | Line 195: | ||
--> | --> | ||
| − | ====Map resolution for the derived beam data object==== | + | ====Map resolution for the derived beam data object:==== |
| − | * < | + | * <i>N</i><sub>side</sub>=1024 for all LFI frequency channels. |
===Comparison of the images of compact sources observed by Planck with FEBeCoP products=== | ===Comparison of the images of compact sources observed by Planck with FEBeCoP products=== | ||
| − | We show here a comparison of the FEBeCoP derived effective beams | + | We show here a comparison of the FEBeCoP-derived effective beams and associated point spread functions (PSF; the transpose of the beam matrix), to the actual images of a few compact sources observed by Planck. The 30GHz frequency channel images are used as an example. We show below a few panels of source images organized as follows: |
| − | * Row | + | * Row 1 – DX9 images of four ERCSC objects, with their Galactic (<i>l</i>,<i>b</i>) coordinates shown under the colour bar; |
| − | * Row | + | * Row 2 – linear scale FEBeCoP PSFs computed using input scanning beams, GRASP beams (GB) for LFI, B-spline (BS) Mars12 beams apodized for the HFI CMB channels, and the BS Mars12 beams for the HFI sub-mm channels (see section Inputs below); |
| − | * Row | + | * Row 3 – log scale of Row 2, PSF iso-contours are shown as solid lines, elliptical Gaussian fit iso-contours are shown as broken lines. |
| − | |||
| − | |||
| − | |||
| + | [[File:30.png| 600px| thumb | center| '''30GHz.''']] | ||
===Histograms of the effective beam parameters=== | ===Histograms of the effective beam parameters=== | ||
| − | Here we present histograms of the three fit parameters | + | Here we present histograms of the three fit parameters – beam FWHM, ellipticity, and orientation with respect to the local meridian and of the beam solid angle. The sky is sampled (quite sparsely) in 768 directions, which were chosen as HEALpix <i>N</i><sub>side</sub>=8 pixel centres for LFI in order to uniformly sample the sky. |
| − | + | Here beam solid angle is estimated according to the definition: '''4π×Σ(effbeam)/max(effbeam)''', | |
| − | + | i.e., | |
| + | <math> 4 \pi \sum(B_{ij}) / {\rm max}(B_{ij}) </math>. | ||
| − | [[File: | + | [[File:DX12_effective_beam_histogram.png | 600px| thumb | center| '''Histograms for LFI effective beam parameters.''' ]] |
| + | ===Sky variation of effective beam solid angle and ellipticity of the best-fit Gaussian=== | ||
| + | Note that the discontinuities at the HEALPix domain edges in the maps are a visual artefact, due to the interplay of the discretized effective beam and the HEALPix pixel grid. | ||
| − | + | [[File:ellipticity_ns8_030_beams_DX12.png| 600px| thumb | center| '''Ellipticity – 30GHz.''']] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | [[File: | ||
| − | |||
| − | |||
| − | |||
===Statistics of the effective beams computed using FEBeCoP=== | ===Statistics of the effective beams computed using FEBeCoP=== | ||
| − | We tabulate the simple statistics of FWHM, ellipticity (e), orientation ( | + | We tabulate the simple statistics of FWHM, ellipticity (<i>e</i>), orientation (ψ), and beam solid angle, (Ω), for a sample of 768 directions on the sky for LFI data. Statistics presented in the table are derived from the histograms shown above: |
| − | |||
| − | |||
| − | |||
| + | * the derived beam parameters are representative of the DPC <i>N</i><sub>side</sub>=1024 HEALPix maps (they include the pixel window function); | ||
| + | * the reported FWHM<sub>eff</sub> values are derived from the beam solid angles, under a Gaussian approximation – these are best used for flux determination, while the Gaussian fits to the effective beam maps are more suited for source identification. | ||
{| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
| − | |+ '''Statistics of the FEBeCoP | + | |+ '''Statistics of the FEBeCoP effective beams computed with the BS Mars12 beams, apodized for the CMB channels and oversampled.''' |
|- | |- | ||
| − | ! ''' | + | ! '''Frequency''' || '''Mean (FWHM)''' [arcmin] || '''σ (FWHM)''' [arcmin] || '''Mean (<i>e</i>)''' || '''σ (<i>e</i>)''' || '''Mean (ψ)''' [deg] || '''σ (ψ)''' [deg] || '''Mean (Ω)''' [arcmin<sup>2</sup>] || '''σ (Ω)''' [arcmin<sup>2</sup>] || '''FWHM<sub>eff</sub>''' [arcmin] |
|- | |- | ||
| − | | 030 || 32. | + | | 030 || 32.288 || 0.021 || 1.315 || 0.031 || 1.347 || 54.074 || 1190.111 || 0.705 || 32.41 |
|- | |- | ||
| − | | 044 || | + | | 044 || 26.997 || 0.583 || 1.190 || 0.030 || 2.088 || 53.905 || 831.611 || 35.041 || 27.09 |
|- | |- | ||
| − | | 070 || 13. | + | | 070 || 13.218 || 0.031 || 1.223 || 0.037 || 2.154 || 54.412 || 200.803 || 0.991 || 13.31 |
|} | |} | ||
| + | ====Beam solid angles for the PCCS==== | ||
| − | + | Ω<sub>eff</sub> is the mean beam solid angle of the effective beam, where beam solid angle is estimated according to the definition: 4πΣ(effective<sub>beam</sub>)/max(effective<sub>beam</sub>), i.e., as an integral over the full extent of the effective beam: | |
| − | + | <math> 4 \pi \sum(B_{ij}) / {\rm max}(B_{ij}) </math>. | |
| − | + | From Ω<sub>eff</sub> we estimate the FWHM<sub>eff</sub> value, under a Gaussian approximation and these are tabulated above. | |
| − | + | The quantity Ω<sup>(1)</sup><sub>eff</sub> is the beam solid angle estimated up to a radius equal to 1×FWHM<sub>eff</sub> and Ω<sup>(2)</sup><sub>eff</sub> is the value up to a radius equal to 2×FWHM<sub>eff</sub>. | |
| − | + | These were estimated according to the procedure followed in the aperture photometry code for the PCCS: if the pixel centre does not lie within the given radius it is not included (so "inclusive=0" in query disc). | |
{|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | {|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
| − | |+'''Band averaged beam solid angles''' | + | |+'''Band-averaged beam solid angles.''' |
| − | | '''Band''' || '''< | + | | '''Band''' || '''Ω<sub>eff</sub> [arcmin<sup>2</sup>]''' || '''Spatial variation [arcmin<sup>2</sup>]''' || '''Ω<sup>(1)</sup><sub>eff</sub> [arcmin<sup>2</sup>]''' || '''Spatial variation-1 [arcmin<sup>2</sup>]''' || '''Ω<sup>(2)</sup><sub>eff</sub> [arcmin<sup>2</sup>]''' || '''Spatial variation-2 [arcmin<sup>2</sup>]''' |
|- | |- | ||
| − | |30 || | + | | 30 || 1190.111 || 0.705 || 1117.876 || 1.968 || 1188.991 || 0.713 |
|- | |- | ||
| − | | 44 || | + | | 44 || 831.611 || 35.041 || 757.891 || 32.782 || 830.767 || 35.074 |
|- | |- | ||
| − | | 70 || 200. | + | | 70 || 200.803 || 0.991 || 186.055 || 1.883 || 200.497 || 0.991 |
|} | |} | ||
| − | ===Related products=== | + | <!-- ===Related products=== --> |
===Monte Carlo simulations=== | ===Monte Carlo simulations=== | ||
| − | FEBeCoP software enables fast, full-sky convolutions of the sky signals with the | + | FEBeCoP software enables fast, full-sky convolutions of the sky signals with the effective beams in the pixel domain. This enables a large number of Monte Carlo simulations of the sky signal maps to be easily generated, convolved with realistically rendered, spatially varying, asymmetric, Planck beams. We performed the following steps: |
| − | * generate the effective beams with FEBeCoP for all frequencies for Nominal Mission data | + | * generate the effective beams with FEBeCoP for all frequencies for Nominal Mission data; |
| − | * generate 100 realizations of maps from a fiducial CMB power spectrum | + | * generate 100 realizations of maps from a fiducial CMB power spectrum; |
| − | * convolve each one of these maps with the effective beams using FEBeCoP | + | * convolve each one of these maps with the effective beams using FEBeCoP; |
| − | * estimate the average of the | + | * estimate the average of the power spectrum of each convolved realization, <i>C</i><sub>ℓ</sub><sup>out</sup>, and 1σ errors. |
| + | Since FEBeCoP enables fast convolutions of the input signal sky with the effective beam, thousands of simulations are generated. These Monte Carlo simulations of the sky signal (that might be CMB or a foreground, such as dust emission), along with LevelS+Madam noise simulations, were used widely for the analysis of Planck data. A suite of simulations were rendered during the mission and tagged as Full Focal Plane simulations. | ||
| − | |||
<!--, FFP#, | <!--, FFP#, | ||
for example [[HL-sims#FFP6 data set|FFP6]]. | for example [[HL-sims#FFP6 data set|FFP6]]. | ||
--> | --> | ||
| − | == Window | + | == Window functions == |
| − | |||
| − | The | + | The "Transfer Function" or the "Beam Window Function" <i>B</i><sub>ℓ</sub> relates the true angular power spectra <i>C</i><sub>ℓ</sub> to the observed angular power spectra <i>Ĉ</i><sub>ℓ</sub>. In the current release, we deliver both TT and EE window functions defined as |
<math> | <math> | ||
| − | + | B_\ell^{TT,EE}= \widetilde{C}_\ell^{TT,EE} / C_\ell^{TT,EE}. | |
\label{eqn:wl1}</math> | \label{eqn:wl1}</math> | ||
| − | Note that | + | Note that the window function can contain a pixel window function (depending on the definition) and it is <i>not</i> the angular power spectra of the scanning beams, although, in principle, one may be able to connect them algebraically. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | The window function computed for the 2018 release has been calculated via simulated timelines. This procedure allow us to include the sidelobes. Procedure and consitency with the once computed with the convolution of teh effective beam is discussed in to {{PlanckPapers|planck2014-a05}}. | ||
| − | [[ | + | Beam window functions are provided in the [[The RIMO#Beam Window Functions|RIMO]]. |
== Sidelobes == | == Sidelobes == | ||
| − | |||
| − | There | + | There are no direct measurements of sidelobes for LFI. The sidelobe patterns for LFI were simulated using GRASP9 multi-reflector GTD. |
| − | We used the RFTM electromagnetic model. Seven beams for each radiometer | + | We used the RFTM electromagnetic model. Seven beams for each radiometer were computed in spherical polar cuts with a step of 0.5° in both θ and φ. |
| − | The beams | + | The beams were computed in the same frames used for the main beams. |
| − | The intermediate beam region (theta < 5 | + | The intermediate beam region (θ < 5°) was replaced with null values. |
| − | + | In the computation we considered: | |
| − | + | *the direct field from the feed; | |
| − | + | *the 1st-order contributions, Bd, Br, Pd, Pr, Sd, Sr, and Fr; | |
| − | + | *the 2nd-order contributions, SrPd, and SdPd. | |
| − | + | Here B = baffle', P = primary reflector, S = secondary reflector, F = focal plane unit box, d = diffraction, and r = reflection. | |
| − | + | For example "Br" means that we considered in the calculation reflections on the telescope baffle system. | |
| − | For example Br | ||
| − | A refinement of the | + | A refinement of the sidelobe model will be considered in a future release, taking into account more contributions, together with physical optics models. |
| − | [[File:slb_lfi_30_27_y_tricromia.png|500px|thumb|centre|''' | + | [[File:slb_lfi_30_27_y_tricromia.png|500px|thumb|centre|'''Image of the LFI27-M sidelobes presented as an RGB picture, where the red channel is 27 GHz (f0), the green channel is 30 GHz (f3), and the blue channel is 33 GHz (f6). Because the combined map does not show any wide white region, the sidelobe pattern changes with frequency, as expected.''']] |
== References == | == References == | ||
| − | |||
<References /> | <References /> | ||
Latest revision as of 15:15, 9 November 2018
Contents
- 1 Overview
- 2 Beam normalization
- 3 Polarized scanning beams and focal plane calibration
- 4 Effective beams
- 4.1 Production process
- 4.2 Inputs
- 4.3 Comparison of the images of compact sources observed by Planck with FEBeCoP products
- 4.4 Histograms of the effective beam parameters
- 4.5 Sky variation of effective beam solid angle and ellipticity of the best-fit Gaussian
- 4.6 Statistics of the effective beams computed using FEBeCoP
- 4.7 Monte Carlo simulations
- 5 Window functions
- 6 Sidelobes
- 7 References
Overview[edit]
LFI observed the sky with 11 pairs of beams associated with the 22 pseudo-correlation radiometers. Each beam of the radiometer pair (Radiometer Chain Assembly - RCA) is labelled as LFIXXM or LFIXXS. Here "XX" is the RCA number ranging from 18 to 28, while "M" and "S" are the two polarizations, namely the main-arm and side-arm of the orthomode transducers [1] (see also LFI naming convention).
Details are given in Planck-2015-A04[2]. Please note that many figures below refer to the Planck release Planck-2013-IV[3], since they have not changed significantly.
Beam normalization[edit]
Following the same procedure applyed during the 2015 release Planck-2015-A04[2] we didn't normalize the beam since up to 1% of the solid angle of the LFI beams falls into the sidelobes, unevenly distributed and concentrated mainly in two areas, namely the main part and sub-spillover.
We employ full 4π beams. Important to note is that roughly 1% of the signal found in the sidelobes is missing from the vicinity of the main beam, so the main beam efficiency η ≈ 99%, which must be accounted for in any analysis of the maps. In particular, the window function used to correct the power spectra extracted from the maps allows for this efficiency.
Details are given in Planck-2015-A04[2].
Polarized scanning beams and focal plane calibration[edit]
Focal plane calibration is based on the determination of the beam pointing parameters in the nominal line of sight (LOS) frame derived from measurements during Jupiter transits. The parameters that characterize the beam pointing are:
- THETA_UV (θuv);
- PHI_UV (φuv).
They are calculated starting from u,v coordinates derived form the beam reconstruction algorithm:
;
.
Two additional angles are used to characterize the beams in the RIMO:
- PSI_UV (ψuv);
- PSI_POL (ψpol).
The angles ψuv and ψpol are not derived from measurements, but rather are estimated from optical simulations. They are the quantities that represent the polarization direction of each beam, assuming that the M- and S-beams of the same RCA point at the same direction on the sky.
The polarized scanning beams were evaluated from optical simulations using the GRASP physical optics code, by appropriately tuning the Radio Frequency Flight Model (RFFM, Planck-PreLaunch-II[4]).
The Radio Frequency Tuned Model (RFTM) was implemented to fit the in-flight beam measurements with an electromagnetic model. The LFI main beams can be considered linearly polarized, but the non-null cross-polarization has an impact on the polarization measurements. Since we are not able to measure the cross-polar beam in flight, we have relied on simulations validated by accurate beam measurements.
The model beams were monochromatic and were computed at various frequencies across a 6-GHz band around the optical centre frequency (OCF) with non-uniform steps (denser sampling where the bandpass was higher). For the RFTM model the OCFs were set at 28.0, 44.0, and 70.0 GHz.
For each simulated beam we created a map of the Stokes polarization parameters. On those maps we performed a weighted in-band average to recover our best estimation of the polarized beam shape. The weighting function was the RIMO transmission function.
The delivered products includes the in-band averaged Stokes parameter scanning maps of main beams, intermediate beams, and sidelobes.
Effective beams[edit]
The 2018 effective beam estimation procedure didn't change with respect 2015 release, new summary values are perfectly in line with the once obtained in the 2015, see Planck-2020-A2[5]. The "effective beam" is the average of all scanning beams pointing at a certain direction within a given pixel of the sky map for a given scan strategy. It takes into account the coupling between azimuthal asymmetry of the beam and the uneven distribution of scanning angles across the sky. It captures the complete information about the difference between the true and observed images of the sky. These beams are, by definition, the objects whose convolution with the true CMB sky produces the observed sky map.
The full algebra involving the effective beams for temperature and polarisation was presented in [6]. Here we summarise the main results. The observed temperature on the sky is a convolution of the true sky and the effective beam :
where
Here t labels the time samples, Ati is 1 if the pointing direction falls in pixel number i, else it is 0, represents the exact pointing direction (not approximated by the pixel centre location), and is the centre of the pixel number j, where the scanning beam is being evaluated (if the pointing direction falls within the cut-off radius of 2.5×FWHM).
The algebra is a bit more involved for polarized detectors. The observed stokes parameters at pixel , , are related to the true Stokes parameters , by the following relation:
where the polarized effective beam matrix
and and are the the polarization weight vectors, as defined in Mitra et al. (2010).[6]
The task is to compute for temperature-only beams and the 3 × 3 matrices for each pixel i, at every neighbouring pixel j that falls within the cut-off radius around the the centre of the ith pixel.
The effective beam is computed by stacking within a small field around each pixel of the HEALPix sky map. Due to the particular features of the Planck scanning strategy, coupled to the beam asymmetries in the focal plane, and data processing of the bolometer and radiometer TOIs, the resulting Planck effective beams vary over the sky.
FEBeCoP, given information on Planck scanning beams and detector pointing during a particular period, provides the pixelized cut-outs of both the effective beam (EB) and the point spread function (PSF), at all pixel-centre positions of the HEALPix-formatted map.
Production process[edit]
The methodology for computing effective beams for a scanning CMB experiment like Planck was presented in Mitra et al. (2010).[6]
FEBeCoP, or the Fast Effective Beam Convolution in Pixel space, is an approach for representing and computing effective beams (including both intrinsic beam shapes and the effects of scanning) that consists of the following steps:
- identify the individual detectors' instantaneous optical response function (presently we use elliptical Gaussian fits of Planck beams from observations of planets, but eventually, an arbitrary mathematical representation of the beam can be used on input);
- follow exactly the Planck scanning, and project the intrinsic beam on the sky at each actual sampling position;
- project instantaneous beams onto the pixelized map over a small region (typically <2.5 FWHM diameter);
- add up all beams that cross the same pixel and its vicinity during the period of interest;
- create a data object of all beams pointed at all Npix directions of pixels in the map at the same resolution for which this precomputation was executed (dimension Npix × a few hundred);
- use the resulting beam object for very fast convolution of all sky signals with the effective optical response of the observing mission.
Computation of the effective beams at each pixel for every detector is a challenging task for high resolution experiments. FEBeCoP is an efficient algorithm the implementation of which enabled us to compute the pixel-based effective beams using moderate computational resources. The algorithm uses different mathematical and computational techniques to bring down the computation cost to a practical level. That allowed several estimations of the effective beams for all Planck detectors for different scan and beam models as well as data sets of different length.
Pixel-ordered detector angles[edit]
The main challenge in computing the effective beams is to go through the trillion samples, which becomes severely limited by I/O. In the first stage, for a given data set, ordered lists of pointing angles are made for each pixel – the Pixel-Ordered Detector Angles (PODA). This is an one-time process for each dataset. We used computers with large memory and used careful memory management bookkeeping to make this step efficient.
effBeam[edit]
The "effBeam" part makes use of the precomputed PODA and unsynchronized reading from the disk to compute the beam. Here we tried to made sure that no repetition occurs in evaluating a trigonometric quantity.
One important reason for separating the two steps is that they use different schemes for parallel computing. The PODA part requires parallelization over time-ordered data samples, while the effBeam part requires distribution of pixels among different computers.
Computational cost[edit]
The whole computation of the effective beams has been performed at the NERSC Supercomputing Center. In the table below we display the computation cost at NERSC for the nominal mission both in terms of CPU hours and in human time.
| Channel | 030 | 044 | 070 |
| PODA/Detector computation time (CPU hours) | 85 | 100 | 250 |
| PODA/Detector computation time (human minutes) | 7 | 10 | 20 |
| Beam/Channel computation time (CPU hours) | 900 | 2000 | 2300 |
| Beam/Channel computation time (human hours) | 0.5 | 0.8 | 1 |
| Convolution computation time (CPU hours) | 1 | 1.2 | 1.3 |
| Convolution computation time (human seconds) | 1 | 1 | 1 |
| Effective beam size (GB) | 173 | 123 | 28 |
The computation cost, especially for PODA and convolution, is heavily limited by the I/O capacity of the disk and so it depends on the overall usage of the cluster.
Inputs[edit]
In order to fix the convention for presentation of the scanning and effective beams, we show the classic view of the Planck focal plane as seen by the incoming CMB photons. The scan direction is marked, and the direction toward the centre of the focal plane is at 85° with respect to the spin axis, pointing upward in the picture.
Focal plane database:[edit]
The Focal Plane DataBase (FPDB) contains information on each detector, e.g., the orientation of the polarization axis, different weight factors, etc. See the instrument RIMOs:
The scanning strategy:[edit]
The scanning strategy, specifically includes the three pointing angles for each detector for each sample. Detector pointings for the nominal mission cover about 15 months of observation from Operational Day (OD) 91 to OD 563 covering 3½ surveys.
Scanning beam:[edit]
The "scanning beam" was modelled for each detector using observations of planets. This was assumed to be constant over the whole mission, although FEBeCoP could be used for a few sets of scanning beams.
- LFI: GRASP scanning beam - the scanning beams used are based on the Radio Frequency Tuned Model (RFTM) smeared to simulate the in-flight optical response. A description of the GRASP beams file formar (.grd) can be found in the "Technical Note PL-LFI-PST-TN-044: LFI Beams Delivery: Format Specifications": File:PST-TN-044 1-0.pdf.
See the instrument RIMOs: The LFI RIMO.
Beam cutoff radii:[edit]
- N times the geometric mean of the FWHM values of all detectors in a channel, where N=2.5 for all LFI frequency channels.
Map resolution for the derived beam data object:[edit]
- Nside=1024 for all LFI frequency channels.
Comparison of the images of compact sources observed by Planck with FEBeCoP products[edit]
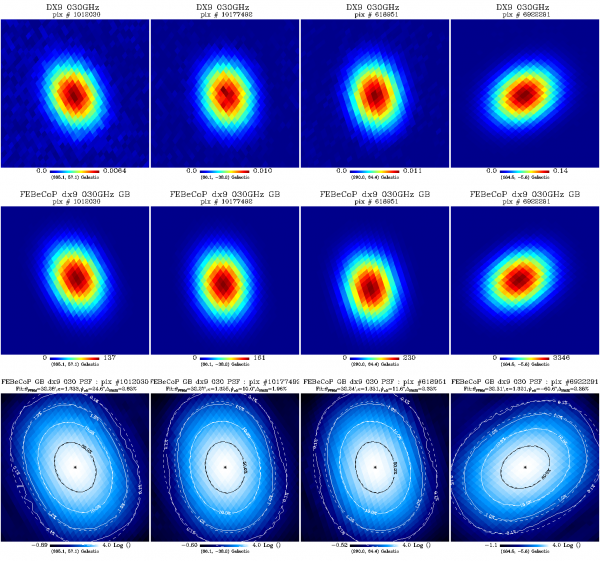
We show here a comparison of the FEBeCoP-derived effective beams and associated point spread functions (PSF; the transpose of the beam matrix), to the actual images of a few compact sources observed by Planck. The 30GHz frequency channel images are used as an example. We show below a few panels of source images organized as follows:
- Row 1 – DX9 images of four ERCSC objects, with their Galactic (l,b) coordinates shown under the colour bar;
- Row 2 – linear scale FEBeCoP PSFs computed using input scanning beams, GRASP beams (GB) for LFI, B-spline (BS) Mars12 beams apodized for the HFI CMB channels, and the BS Mars12 beams for the HFI sub-mm channels (see section Inputs below);
- Row 3 – log scale of Row 2, PSF iso-contours are shown as solid lines, elliptical Gaussian fit iso-contours are shown as broken lines.
Histograms of the effective beam parameters[edit]
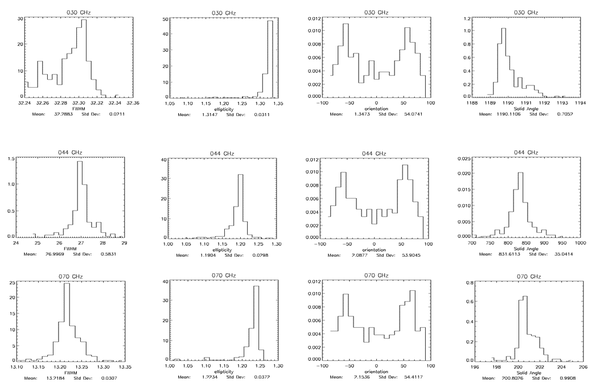
Here we present histograms of the three fit parameters – beam FWHM, ellipticity, and orientation with respect to the local meridian and of the beam solid angle. The sky is sampled (quite sparsely) in 768 directions, which were chosen as HEALpix Nside=8 pixel centres for LFI in order to uniformly sample the sky.
Here beam solid angle is estimated according to the definition: 4π×Σ(effbeam)/max(effbeam), i.e.,
.
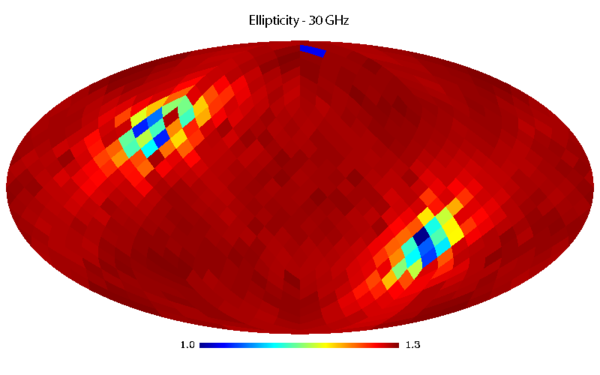
Sky variation of effective beam solid angle and ellipticity of the best-fit Gaussian[edit]
Note that the discontinuities at the HEALPix domain edges in the maps are a visual artefact, due to the interplay of the discretized effective beam and the HEALPix pixel grid.
Statistics of the effective beams computed using FEBeCoP[edit]
We tabulate the simple statistics of FWHM, ellipticity (e), orientation (ψ), and beam solid angle, (Ω), for a sample of 768 directions on the sky for LFI data. Statistics presented in the table are derived from the histograms shown above:
- the derived beam parameters are representative of the DPC Nside=1024 HEALPix maps (they include the pixel window function);
- the reported FWHMeff values are derived from the beam solid angles, under a Gaussian approximation – these are best used for flux determination, while the Gaussian fits to the effective beam maps are more suited for source identification.
| Frequency | Mean (FWHM) [arcmin] | σ (FWHM) [arcmin] | Mean (e) | σ (e) | Mean (ψ) [deg] | σ (ψ) [deg] | Mean (Ω) [arcmin2] | σ (Ω) [arcmin2] | FWHMeff [arcmin] |
|---|---|---|---|---|---|---|---|---|---|
| 030 | 32.288 | 0.021 | 1.315 | 0.031 | 1.347 | 54.074 | 1190.111 | 0.705 | 32.41 |
| 044 | 26.997 | 0.583 | 1.190 | 0.030 | 2.088 | 53.905 | 831.611 | 35.041 | 27.09 |
| 070 | 13.218 | 0.031 | 1.223 | 0.037 | 2.154 | 54.412 | 200.803 | 0.991 | 13.31 |
Beam solid angles for the PCCS[edit]
Ωeff is the mean beam solid angle of the effective beam, where beam solid angle is estimated according to the definition: 4πΣ(effectivebeam)/max(effectivebeam), i.e., as an integral over the full extent of the effective beam:
.
From Ωeff we estimate the FWHMeff value, under a Gaussian approximation and these are tabulated above. The quantity Ω(1)eff is the beam solid angle estimated up to a radius equal to 1×FWHMeff and Ω(2)eff is the value up to a radius equal to 2×FWHMeff. These were estimated according to the procedure followed in the aperture photometry code for the PCCS: if the pixel centre does not lie within the given radius it is not included (so "inclusive=0" in query disc).
| Band | Ωeff [arcmin2] | Spatial variation [arcmin2] | Ω(1)eff [arcmin2] | Spatial variation-1 [arcmin2] | Ω(2)eff [arcmin2] | Spatial variation-2 [arcmin2] |
| 30 | 1190.111 | 0.705 | 1117.876 | 1.968 | 1188.991 | 0.713 |
| 44 | 831.611 | 35.041 | 757.891 | 32.782 | 830.767 | 35.074 |
| 70 | 200.803 | 0.991 | 186.055 | 1.883 | 200.497 | 0.991 |
Monte Carlo simulations[edit]
FEBeCoP software enables fast, full-sky convolutions of the sky signals with the effective beams in the pixel domain. This enables a large number of Monte Carlo simulations of the sky signal maps to be easily generated, convolved with realistically rendered, spatially varying, asymmetric, Planck beams. We performed the following steps:
- generate the effective beams with FEBeCoP for all frequencies for Nominal Mission data;
- generate 100 realizations of maps from a fiducial CMB power spectrum;
- convolve each one of these maps with the effective beams using FEBeCoP;
- estimate the average of the power spectrum of each convolved realization, Cℓout, and 1σ errors.
Since FEBeCoP enables fast convolutions of the input signal sky with the effective beam, thousands of simulations are generated. These Monte Carlo simulations of the sky signal (that might be CMB or a foreground, such as dust emission), along with LevelS+Madam noise simulations, were used widely for the analysis of Planck data. A suite of simulations were rendered during the mission and tagged as Full Focal Plane simulations.
Window functions[edit]
The "Transfer Function" or the "Beam Window Function" Bℓ relates the true angular power spectra Cℓ to the observed angular power spectra Ĉℓ. In the current release, we deliver both TT and EE window functions defined as
Note that the window function can contain a pixel window function (depending on the definition) and it is not the angular power spectra of the scanning beams, although, in principle, one may be able to connect them algebraically.
The window function computed for the 2018 release has been calculated via simulated timelines. This procedure allow us to include the sidelobes. Procedure and consitency with the once computed with the convolution of teh effective beam is discussed in to Planck-2015-A04[2].
Beam window functions are provided in the RIMO.
Sidelobes[edit]
There are no direct measurements of sidelobes for LFI. The sidelobe patterns for LFI were simulated using GRASP9 multi-reflector GTD. We used the RFTM electromagnetic model. Seven beams for each radiometer were computed in spherical polar cuts with a step of 0.5° in both θ and φ. The beams were computed in the same frames used for the main beams. The intermediate beam region (θ < 5°) was replaced with null values.
In the computation we considered:
- the direct field from the feed;
- the 1st-order contributions, Bd, Br, Pd, Pr, Sd, Sr, and Fr;
- the 2nd-order contributions, SrPd, and SdPd.
Here B = baffle', P = primary reflector, S = secondary reflector, F = focal plane unit box, d = diffraction, and r = reflection. For example "Br" means that we considered in the calculation reflections on the telescope baffle system.
A refinement of the sidelobe model will be considered in a future release, taking into account more contributions, together with physical optics models.
References[edit]
- ↑ The Planck-LFI flight model ortho-mode transducers, O. D'Arcangelo, A. Simonetto, L. Figini, E. Pagana, F. Villa, M. Pecora, P. Battaglia, M. Bersanelli, R. C. Butler, S. Garavaglia, P. Guzzi, N. Mandolesi, C. Sozzi, Journal of Instrumentation, 4, 2005-+, (2009).
- ↑ 2.02.12.22.3 Planck 2015 results. IV. LFI beams and window functions, Planck Collaboration, 2016, A&A, 594, A4.
- ↑ Planck 2013 results. IV. Low Frequency Instrument beams and window functions, Planck Collaboration, 2014, A&A, 571, A4.
- ↑ Planck pre-launch status: The optical system, J. A. Tauber, H. U. Nørgaard-Nielsen, P. A. R. Ade, et al. , A&A, 520, A2+, (2010).
- ↑ Planck 2018 results. II. Low Frequency Instrument data processing, Planck Collaboration, 2020, A&A, 641, A2.
- ↑ 6.06.16.2 Fast Pixel Space Convolution for Cosmic Microwave Background Surveys with Asymmetric Beams and Complex Scan Strategies: FEBeCoP, S. Mitra, G. Rocha, K. M. Górski, K. M. Huffenberger, H. K. Eriksen, M. A. J. Ashdown, C. R. Lawrence, ApJS, 193, 5-+, (2011).
(Planck) Low Frequency Instrument
LFI Radiometer Chain Assembly
Line Of Sight
reduced IMO
Cosmic Microwave background
Full-Width-at-Half-Maximum
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
Operation Day definition is geometric visibility driven as it runs from the start of a DTCP (satellite Acquisition Of Signal) to the start of the next DTCP. Given the different ground stations and spacecraft will takes which station for how long, the OD duration varies but it is basically once a day.
Early Release Compact Source Catalog
(Planck) High Frequency Instrument
Data Processing Center