Map-making LFI
Contents
[hide]- 1 Map-making
- 2 Low-resolution maps and Noise Covariance Matrices
- 3 Half-ring jackknife Noise Maps
- 4 Noise Monte Carlo Simulation
- 5 References
Map-making[edit]
The input of the map-making step consists of the calibrated timelines, along with the corresponding pointing information. The main output consists of temperature and polarization maps. An important part of the map-making step is the removal of correlated 1/$f$ noise.
LFI maps were constructed with the Madam map-making code, version 3.7.4. The code is based on generalized destriping technique, where the correlated noise component is modeled as a sequence of constant offset, "baselines". The baseline solution is constrained by a noise filter. As auxiliary information the code produces a hit count map and a white noise covariance matrix. No beam information is used, but the signal is assigned to the pixel where the center of the beam falls.
In the first release the chosen baseline length was one second. This gives a good noise removal, without being computationally heavy. The noise filter was built according to the noise parameters listed in Table 1.
Flagged samples were excluded from the analysis. The galaxy region was masked out in the destriping phase, to reduce error arising from strong signal gradients. Radiometers were combined according to the horn-uniform weighting scheme to minimize systematics. The polarization component was included in the analysis, although only the temperature maps are released. A detailed description of the map-making procedure is given in Planck-2013-II[1]. See also section Frequency Maps.
The maps are in Healpix format, at resolution $N_{\rm side}$=1024, in nested pixeling scheme. Unobserved pixels are marked by a special value.
The released maps are in galactic coordinates. The conversion from ecliptic to galactic coordinate system is described by rotation matrix $
\newcommand{\Re}{\mathrm{Re}\,}
\newcommand{\pFq}[5]{{}_{#1}\mathrm{F}_{#2} \left( \genfrac{}{}{0pt}{}{#3}{#4} \bigg| {#5} \right)}
$ \begin{align}
\label{def:Rot_matrix}
\left (\begin{matrix}
-0.054882486 & 0.494116468 & -0.867661702\\
-0.993821033 & -0.110993846 & -0.000346354\\
-0.096476249 & 0.86228144 & 0.497154957
\end{matrix} \right).
\end{align} The conversion was applied to the input pointing data, prior to the construction of the map.
| Radiometer | White noise sigma [mK$_{\rm CMB}$] | Slope | Knee frequency [mHz] | $f_{\rm min}$ [Hz] | Horn-uniform weight |
|---|---|---|---|---|---|
| LFI18M | 4.542 | -1.07 | 15.3 | 1.15e-5 | 5.297E+04 |
| LFI18S | 4.139 | -1.20 | 18.3 | 1.15e-5 | 5.297E+04 |
| LFI19M | 5.146 | -1.22 | 11.9 | 1.15e-5 | 3.948E+04 |
| LFI19S | 4.918 | -1.12 | 14.6 | 1.15e-5 | 3.948E+04 |
| LFI20M | 5.214 | -1.31 | 8.4 | 1.15e-5 | 3.482E+04 |
| LFI20S | 5.500 | -1.34 | 6.0 | 1.15e-5 | 3.482E+04 |
| LFI21M | 4.008 | -1.26 | 39.3 | 1.15e-5 | 4.897E+04 |
| LFI21S | 4.978 | -1.24 | 14.0 | 1.15e-5 | 4.897E+04 |
| LFI22M | 4.348 | -1.53 | 10.1 | 1.15e-5 | 4.864E+04 |
| LFI22S | 4.713 | -1.20 | 15.9 | 1.15e-5 | 4.864E+04 |
| LFI23M | 4.468 | -1.07 | 30.2 | 1.15e-5 | 4.670E+04 |
| LFI23S | 4.782 | -1.21 | 58.8 | 1.15e-5 | 4.670E+04 |
| LFI24M | 3.145 | -0.94 | 26.9 | 1.15e-5 | 1.158E+05 |
| LFI24S | 2.717 | -0.91 | 73.0 | 1.15e-5 | 1.158E+05 |
| LFI25M | 2.821 | -0.85 | 20.1 | 1.15e-5 | 1.319E+05 |
| LFI25S | 2.684 | -0.90 | 46.1 | 1.15e-5 | 1.319E+05 |
| LFI26M | 3.280 | -0.92 | 64.4 | 1.15e-5 | 1.056E+05 |
| LFI26S | 2.859 | -0.88 | 43.8 | 1.15e-5 | 1.056E+05 |
| LFI27M | 1.609 | -0.93 | 175.1 | 1.15e-5 | 3.567E+05 |
| LFI27S | 1.737 | -0.91 | 109.6 | 1.15e-5 | 3.567E+05 |
| LFI28M | 1.814 | -0.93 | 127.9 | 1.15e-5 | 3.353E+05 |
| LFI28S | 1.635 | -0.91 | 43.9 | 1.15e-5 | 3.353E+05 |
Low-resolution maps and Noise Covariance Matrices
To fully exploit the information contained in the large scale structure of the microwave sky, a pixel-pixel covariances are needed in the maximum likelihood estimation of the CMB power spectrum. However, full covariance matrices are impossible to employ at the native map resolution due to resource limitations. A low-resolution dataset is therefore required at the low-$l$ analysis. This dataset consists of low-resolution maps, and descriptions of residual noise present in those maps given by pixel-pixel noise covariance matrices (NCVMs).
The low-resolution dataset can currently be utilized efficiently only at resolution $N_{\rm side} = 16$, or lower. All the low-resolution data products are produced at this target resolution.
Low Resolution Maps
Number of different schemes to obtain the low resolution maps are discussed in[2]. We chose to downgrade the maps using the inverse noise weighting. See Planck-2013-II[1] for discussion.
Inputs
We took the high resolution maps described in Map-making and Frequency Maps, and the corresponding $3 \times 3$ matrices as an input for this analysis step.
Production
The high resolution maps were downgraded to $N_\mathrm{side} = 16$ using inverse noise weights (given by the $3 \times 3$ matrices), and subsequently the temperature part was smoothed with a symmetric Gaussian beam with $\mbox{FWHM} = 440\,\mbox{arcmin}$.
Noise Covariance Matrices
The statistical description of the residual noise in the maps is given in the form of a pixel-to-pixel noise covariance matrix (NCVM), as described in[2].
Inputs
The noise model was given in the form of the three noise parameters: white noise level $\sigma$, slope, and knee frequency $f_{\rm knee}$. We actually used three sets of noise parameters one for the entire mission (noise parameters are listed in Table 1), and one per each sky survey (SS1 and SS2).
We used the same pointing as in the noise Monte Carlo simulations. See the description in Noise Monte Carlo Simulation Inputs.
We used the gap files produced during the making of the flight maps to leave out samples that were flagged bad for various reasons.
Production
The output of the NCVM module of Madam map-maker are inverse NCVMs. Since the inverse matrices are additive, we divided the computations into a number of small chucks to save computational resources. Therefore we firstly calculated one inverse NCVM per radiometer per survey at resolution $N_\mathrm{side}=32$, and secondly combined the individual inverse matrices to form the actual inverse matrices. The map-making parameters were almost identical to the standard map-making runs. The differing parameter values are listed below:
- Baseline lengths were 0.25 s (8 samples), 0.50 s (24 samples), and 0.50 s (39 samples) for 30 GHz, 44 GHz, and 70GHz, respectively.
- The calculations were performed at resolution $N_\mathrm{side} = 32$.
- No destriping mask was applied.
- The horns were weighted optimally.
To get the noise covariance from its inverse, the matrices are inverted using the eigen decomposition of a matrix. The monopole of the temperature map cannot be resolved by the map-maker, and thus the matrix becomes singular. The ill-determined mode is left out of the analysis.
Having calculated the eigen decomposition in the previous step, we can apply the same linear operators to modify the eigenvectors as was applied to the high resolution maps while downgrading them. The eigenvectors are downgraded to $N_\mathrm{side} = 16$ using inverse noise weights, and subsequently the temperature part is smoothed with a symmetric Gaussian beam with $\mbox{FWHM} = 440\,\mbox{arcmin}$.
The final matrices are then recomposed from the original eigenvalues and modified eigenvectors.
The low resolution noise covariance matrices
- are in C binary format files.
- are organized in block form,
$
\newcommand{\Re}{\mathrm{Re}\,}
\newcommand{\pFq}[5]{{}_{#1}\mathrm{F}_{#2} \left( \genfrac{}{}{0pt}{}{#3}{#4} \bigg| {#5} \right)}
$ \begin{align}
\label{def:Block_form}
\left (\begin{matrix}
II & IQ & IU \\
QI & QQ & QU \\
UI & UQ & UU
\end{matrix} \right).
\end{align}
- are in HEALPix nested pixelisation scheme. Resolution is $N_\mathrm{side} = 16$, and thus there are $N_\mathrm{pix} = 3072$ pixels.
- are in Galactic coordinates.
- have units $\mathrm{K}_{\mathrm{CMB}}$.
Half-ring jackknife Noise Maps
Overview
In order to estimate the noise directly at the map level and in the angular power spectra, we divided the time-ordered data into two halves and produced half-ring jackknife maps as described in Planck First Results: II. The Low Frequency Instrument performance and data processing.
Briefly: Instead of using the full time ordered data as described above, we produced two sets of maps using either only the first half of each pointing period (map named $\mathbf{j_1}$ below) or only the second half of each pointing period (map named $\mathbf{j_2}$). At each pixel $p$, these half-ring jackknife maps $\mathbf{j_1}$ and $\mathbf{j_2}$ contain the same sky signal, since they result from the same scanning pattern on the sky. However, because of instrumental noise, the maps $\mathbf{j_1}$ and $\mathbf{j_2}$ are not identical.
We estimated the noise level in each map $\mathbf{m}$ made using the full(ring) data, by constructing a half-ring difference map
$\mathbf{n_{m}}(p) = [ \mathbf{j_1}(p) - \mathbf{j_2}(p)] \ / \ \mathbf{w_{\rm hit}}(p)\,,$
with weights
$\mathbf{w_{hit}}(p) = \sqrt{ \mathbf{hit_{full}}(p) \left[ \frac{1}{\mathbf{hit_1}(p)} +
\frac{1}{\mathbf{hit_2}(p)} \right]}\,$.
Here $\mathbf{hit_{full}}(p) = \mathbf{hit_1}(p) + \mathbf{hit_2}(p)$ is the hit count at pixel $p$ in the full map $\mathbf{m}$, while $\mathbf{hit_1}$ and $\mathbf{hit_2}$ are the hit counts of $\mathbf{j_1}$ and $\mathbf{j_2}$, respectively. The weight factor $\mathbf{w_{hit}}(p)$ is equal to $2$ only in those pixels where $\mathbf{hit_1}(p) = \mathbf{hit_2}(p)$. In a typical pixel, $\mathbf{hit_1}(p)$ will differ slightly from $\mathbf{hit_2}(p)$ and hence the weight factor is $\mathbf{w_{hit}}(p) > 2$.
The half-ring difference maps $\mathbf{n_{m}}$ are the most direct measure of the noise in the actual maps. The other noise estimates (NCVM and noise Monte Carlo) rely on specific modelling of the noise and this modelling can be validated by comparing to the half-ring difference maps. However, the half-ring difference maps can only capture the noise that varies faster than half of the duration of the pointing period, i.e., the noise whose frequency is $f \gtrsim 1/20\,\mbox{min} = 0.85\,$mHz.
We calculated the noise maps $\mathbf{n_{m}}$, from half-ring jackknife maps for temperature (I) and polarization (Q and U) and as a first quality check of the maps (and as one of the tests of the whole data processing pipeline up to the maps) tested both numerically and visually that these noise maps divided pixel-by-pixel by square root of the white noise covariance maps were approximately Gaussian with variance near to unity. Temperature noise maps for the nominal survey and for the first and second sky surveys are shown in the next subsection. Further we calculated from the noise maps the temperature and polarization (E and B mode) auto-correlation and cross-correlation noise angular power spectra by anafast and compared to these the results from the white noise covariance matrices and from the noise Monte Carlo simulations. A similar comparison was made between downgraded half-ring noise maps, downgraded noise Monte Carlo maps and the low resolution noise covariance maps. Detailed results are presented in the Systematic Effects paper.
Examples of Half-ring Difference Maps and Noise Angular Power Spectra[edit]
Hit Count Weighted Half-ring Difference Maps[edit]
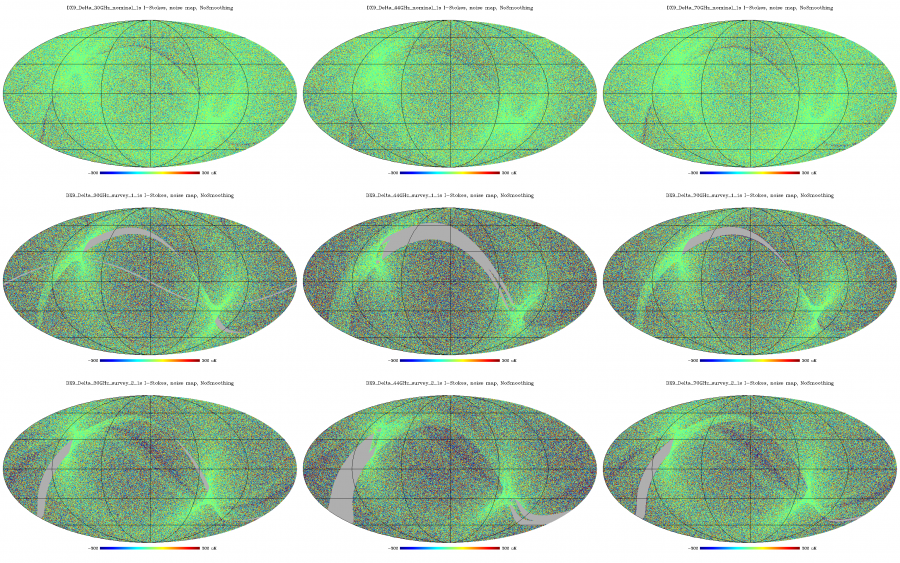
Here we show some hitcount weighted half-ring difference maps, i.e., noise maps for temperature. The columns are for different LFI frequencies: 30, 44, and 70 GHz. The rows are the nominal survey (a bit more than 1 year of observations), survey 1 (the first sky survey, approx first half a year of observations) and survey 2 (the second sky survey, approx the second half a year of observations). Some features are visible in particular in the galactic plane. These are due to "gradient leakage". (In regions where the gradient in the sky signal is very large even a tiny difference in the pointing of the first and second half of each pointing period causes the signal to "leak" to the half-ring difference map. In practice this is not a problem for noise estimation, since these regions - the galaxy, orion, crab nebula, etc - will be masked in the cosmology analysis.
Half-ring difference maps calculated at the native nside 1024 resolution. Columns: frequency (30, 44, 70 GHz), rows: sky survey (nominal, survey_1, survey_2).
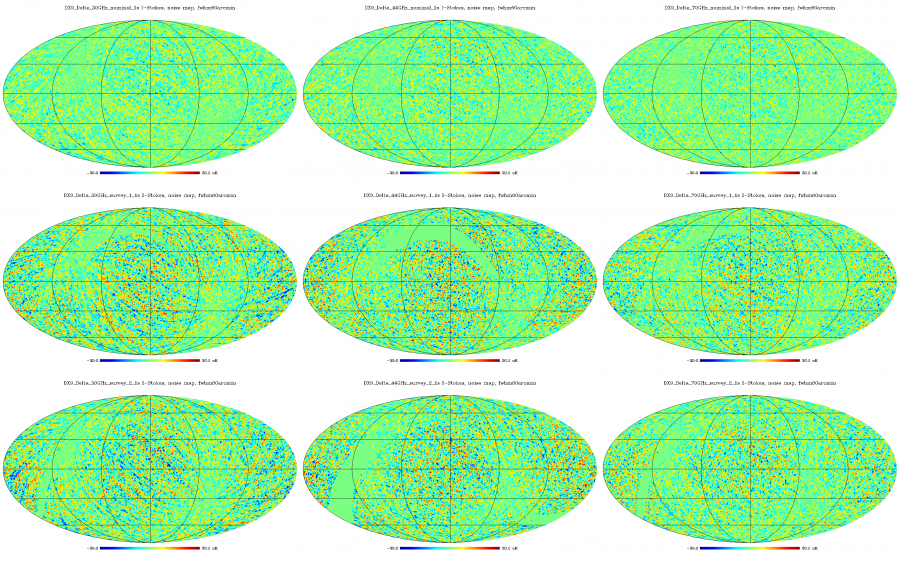
Half-ring difference maps (the same as above, but) smoothed with 60 arcmin fwhm Gaussian. Columns: frequency (30, 44, 70 GHz), rows: sky survey (nominal, survey_1, survey_2).
Hit Count Weighted Half-ring Difference Maps Normalized by sqrt of white noise variance at each pixel[edit]
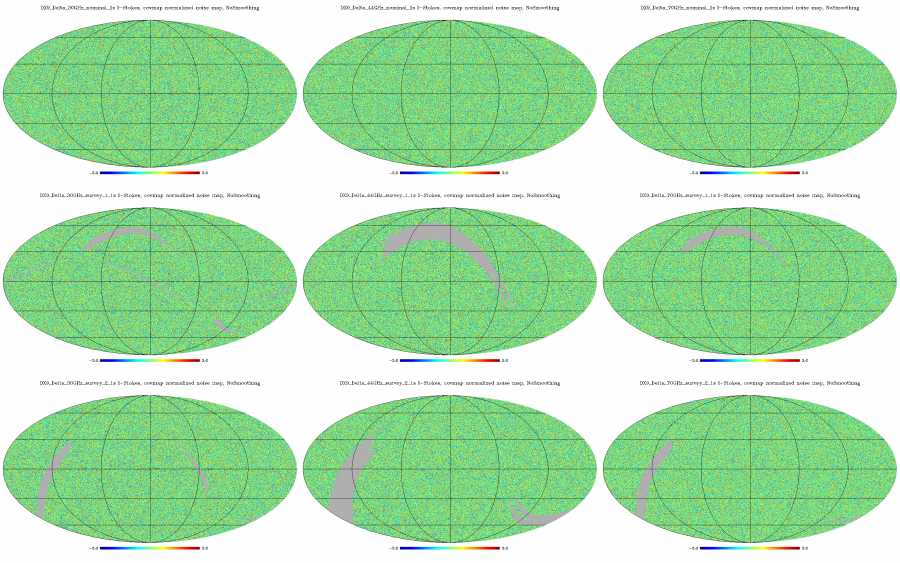
Now we show the same as above, but divided by the square root of the estimate of white noise variance in each pixel. These normalized noise maps should be approximately Gaussian with a unit variance (at the native resolution), apart from some stripes that are due to correlated (non-Gaussian) noise. The large-scale noise is more apparent in the smoothed version of the figure that follows after the native resolution version.
Normalized Half-ring difference maps calculated at the native nside 1024 resolution. Columns: frequency (30, 44, 70 GHz), rows: sky survey (nominal, survey_1, survey_2).
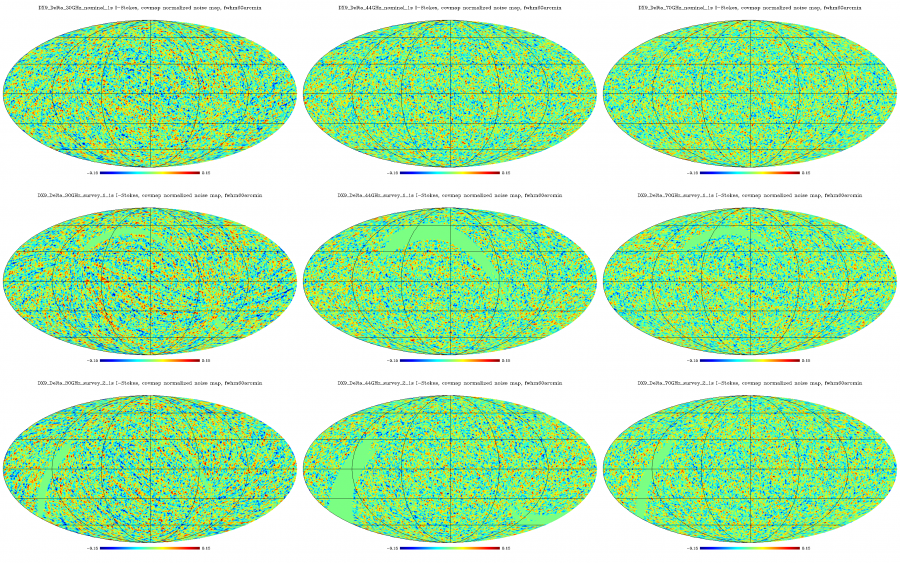
Normalized Half-ring difference maps (the same as above, but) smoothed with 60 arcmin fwhm Gaussian. Columns: frequency (30, 44, 70 GHz), rows: sky survey (nominal, survey_1, survey_2).
Noise Angular Power Spectra from Half-ring Difference Maps[edit]
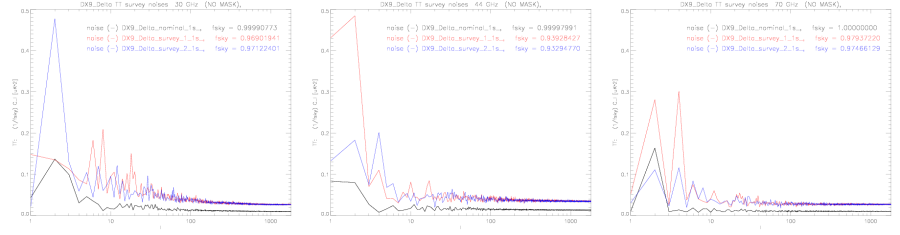
The noise angular power spectra calculated by anafast from half-ring difference temperature maps and normalized by the sky coverage to estimate the noise level if there was a full sky coverage in order to make a comparison of different surveys easier. Columns: frequency (30, 44, 70 GHz). Colors: black = nominal, red = survey_1, blue = survey_2.
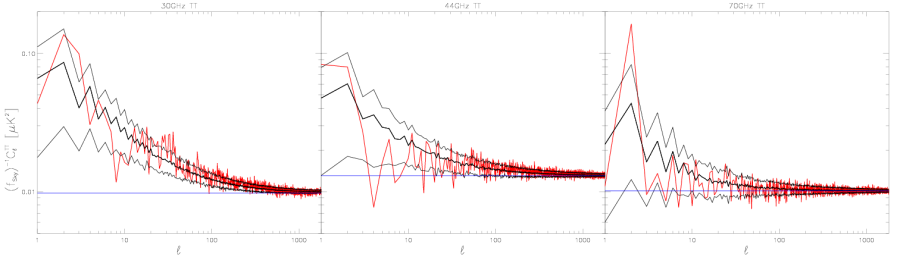
Comparison of Noise Calculated from Half-ring Difference and from Other Noise Estimates[edit]
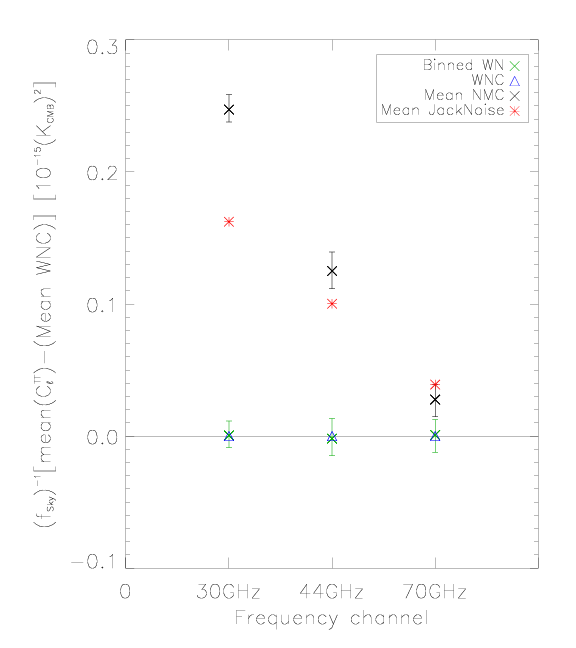
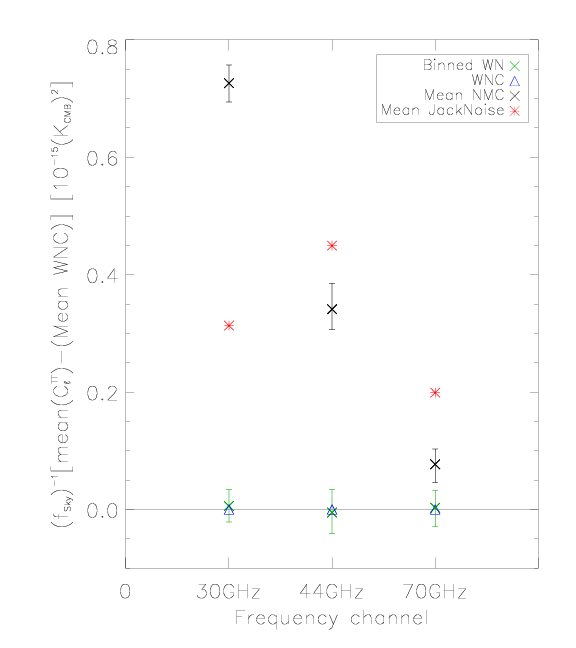
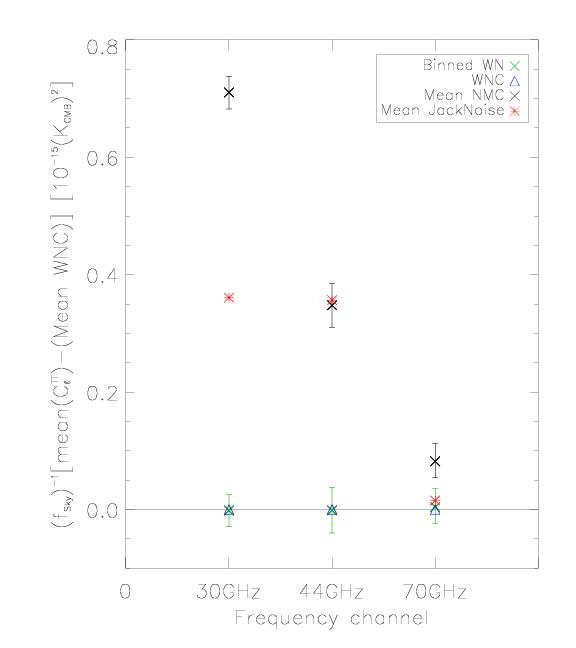
Here we compare noise angular power spectra estimated from half-ring difference maps (RED) to the estimate from white noise covariance maps (BLUE) and the full noise Monte Carlo simulations (BLACK, top curve 16% quantile, middle curve 50% quantile, i.e., median, and bottom curve 84% quantile) - see the next section for the details of noise Monte Carlo.
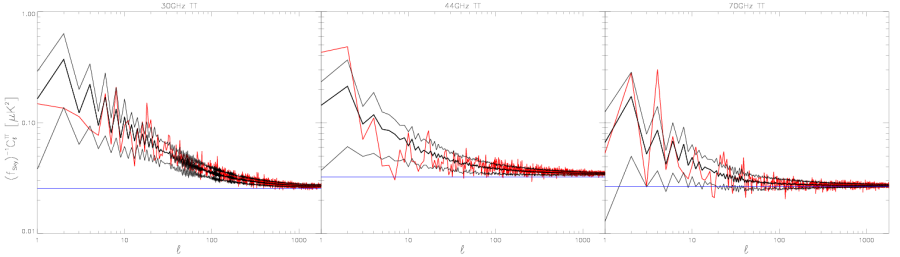
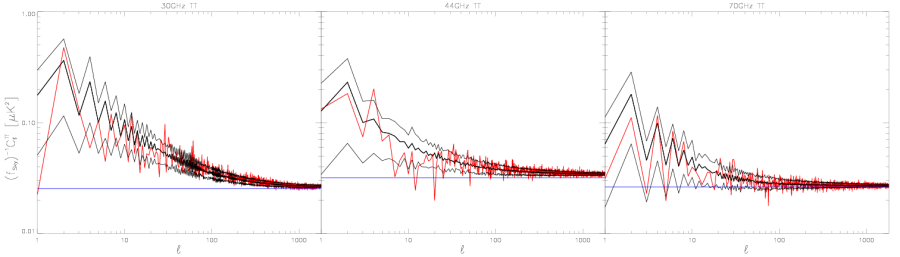
High-ell average () noise relative to the white noise estimate[edit]
The same as previous figures, but the noise comparison made from the high ell tails off the angular power spectra where the white noise dominates. We have taken the average of from the multipoles between 1150 and 1800, and subtracted the white noise estimate. Half-ring difference noise estimate is RED, the full noise Monte Carlo estimate is BLACK, and the white noise estimate from noise Monte Carlo is GREEN. The white noise estimate from the white noise covariance map (WNC), BLUE, has been subtracted from all the results.
Noise Monte Carlo Simulation[edit]
Overview[edit]
Calculating and handling full pixel-to-pixel noise covariance matrices for Planck maps if feasible only at low resolution. To support the analysis of high-resolution maps, a Monte Carlo set of noise maps were produced. These maps were produced from noise timelines using the same map-making procedure as for the flight data. In the noise Monte Carlo it was possible to follow exactly the map-making procedure used for the flight maps, whereas for the calculation of noise covariance matrices some approximations had to be made. Such noise Monte Carlos were produced at two levels of the analysis: 1) LFI Monte Carlo (MC) as part of the LFI data processing, and 2) Full Focal Plane (FFP) Monte Carlo as part of the joint HFI/LFI data processing. This page describes the LFI noise MC. For the FFP MC, see HL-sims and Simulation data.
Inputs[edit]
The noise MC uses a three-parameter (white noise level ($\sigma$), slope, and knee frequency ($f_\mathrm{knee}$)) noise model, where the noise consists of white noise and correlated ($1/f$) noise and the latter has a power spectrum
- $ P(f) = \frac{2\sigma^2}{f_\mathrm{sample}}\left(\frac{f}{f_\mathrm{knee}}\right)^\mathrm{slope} $.
Here $f_\mathrm{sample}$ is the sampling frequency of the instrument. The noise parameters were determined separately for each radiometer as described in Noise, assuming they stayed constant over the mission.
The detector pointing was reconstructed from satellite pointing, focal-plane geometry, pointing correction (tilt angle), and sample timing, using Level-S simulation software. The same pointing solution (two focal planes) was used as for the LFI flight maps. Due to numerical accuracy, the detector pointing in the noise MC was not exactly the same as for the flight maps, but some data samples (of the order of one in a thousand) whose pointing was near the pixel boundary ended up assigned to the neighboring pixel. During the map-making from the flight data, a gap file was produced to represent the samples that were omitted from map-making due to various flags. This gap file was used in the noise MC instead of the full set of flags. The flight map-making used a destriping mask to exclude regions of strong signal gradients from contributing to the noise baseline solution. These same destriping masks (one for each frequency channel) were used for the noise MC.
Production[edit]
The noise was generated internally in the Madam map-making code using a Stochastic Differential Equation (SDE) method, to avoid time-consuming writing and reading noise timelines to/from disk. Noise for each pointing period was generated separately, using a double-precision random number seed constructed from the realization number, radiometer number, and the pointing period number; to allow regeneration of the same noise realization when needed. White noise and $1/f$ noise were generated separately.
The same map-making code (Madam) with the same parameter settings was used for the noise MC as for the flight maps. In addition to the destriped maps from the full noise (output maps), also binned maps from just the white noise (binned white noise maps) were produced; they represent the white noise part of the output maps. The difference between these two maps represent the residual correlated noise in the output map. The maps were made at Healpix resolution $N_\mathrm{side} = 1024$. For low-resolution analysis, these maps were downgraded (and the temperature part was smoothed) to $N_\mathrm{side} = 32$ and $N_\mathrm{side} = 16$.
In addition to frequency maps for the nominal survey, also single-survey and 70 GHz horn-pair maps were produced in the noise MC. For each case 102--1026 realizations were produced.
Usage[edit]
These noise Monte Carlo maps were used for a number of things in LFI data analysis. They were compared to the low-resolution noise covariance matrices, generated for the same noise model to see the impact of the approximations in the noise covariance matrix calculation. They were compared to the half-ring noise maps to see how well the noise model matches the noise in the flight maps (noting, however, that the half-ring noise maps misrepresent the lowest noise frequencies in the flight maps, and contain some effects from the sky signal). They were also used in power spectrum estimation and non-Gaussianity estimation.
Examples[edit]
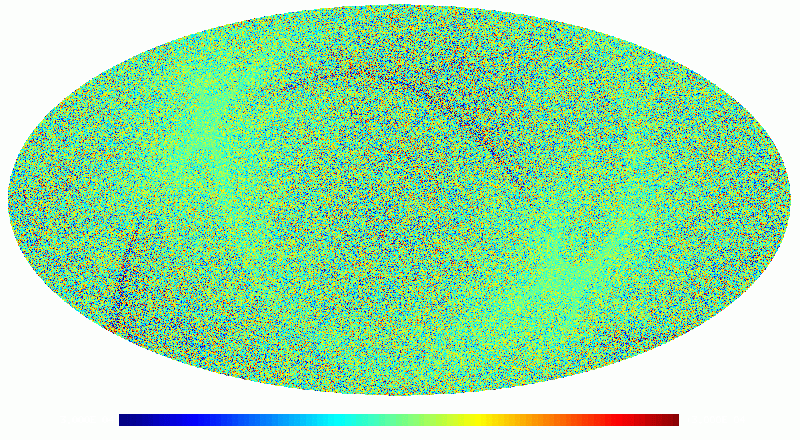
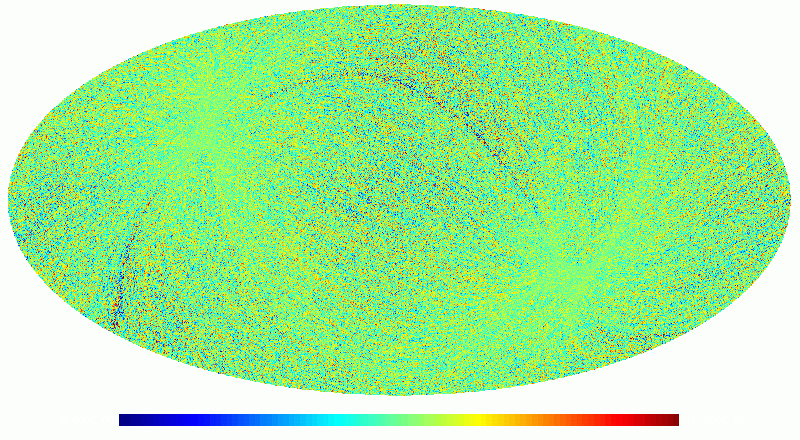
As an example, we show below images of the first realization of the 70 GHz frequency map noise for the nominal survey. The images are in order: destriped full noise, binned white noise, residual correlated noise. Note that it is difficult to see any difference between the first too images, since the residual correlated noise is more than an order of magnitude below the white noise level. The units are CMB K.
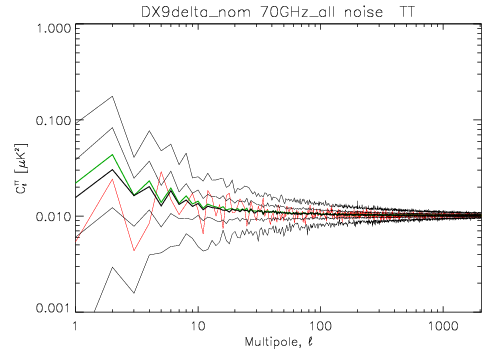
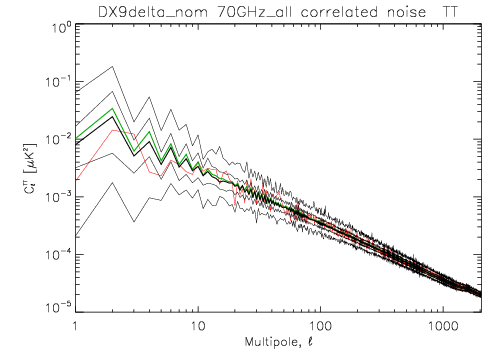
The following two images show the statistics of the angular power spectra of 101 realizations of the 70 GHz frequency map noise for the nominal survey. The thick black line shows the median $C_\ell$, and the green line the mean $C_\ell$. Thin black lines show the minimum, 16% quantile, 84% quantile, and the maximum $C_\ell$. The red line is the 102$^{nd}$ realization. The first plot is for the full noise in the output map, the second plot is for the residual correlated noise.
References[edit]
- ↑ Jump up to: 1.01.1 Planck 2013 results: The Low Frequency Instrument data processing, Planck Collaboration 2013 II, A&A, in press, (2014).
- ↑ Jump up to: 2.02.1 Residual noise covariance for Planck low-resolution data analysis, R. Keskitalo, M. A. J. Ashdown, P. Cabella, T. Kisner, T. Poutanen, R. Stompor, ArXiv e-prints, (2013).
(Planck) Low Frequency Instrument
Cosmic Microwave background
Full-Width-at-Half-Maximum
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
(Planck) High Frequency Instrument