Difference between revisions of "Simulation data"
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== Introduction == | == Introduction == | ||
| − | |||
| − | The | + | |
| − | + | The 2015 Planck data release is supported by a set of simulated maps of the sky, by astrophysical component, and of that sky as seen by Planck (fiducial mission realizations), together with separate sets of Monte Carlo realizations of the CMB and the instrument noise. | |
| − | + | ||
| − | + | Currently, only a subset of these simulations is available from the Planck Legacy Archive. In particular: | |
| + | * 18000 full mission CMB simulations: 1000 for each of the nine Planck frequencies, and for two different sets of cosmological parameters. | ||
| + | * 9000 full mission noise simulations: 1000 for each of the nine Planck frequencies. | ||
| + | * 18 full mission sky simulated maps: two sets of sky maps with and without bandpass corrections applied. | ||
| + | |||
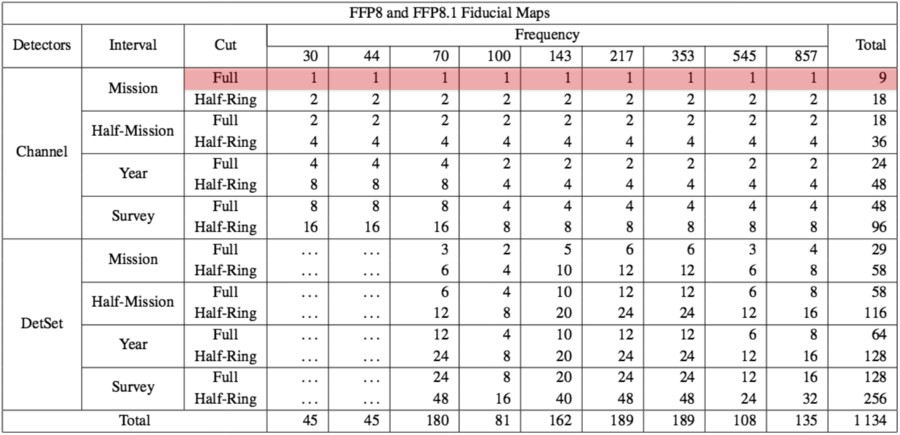
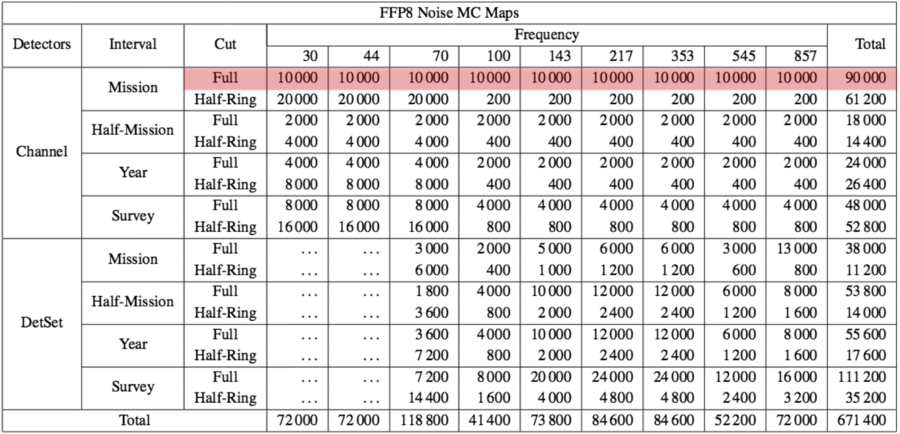
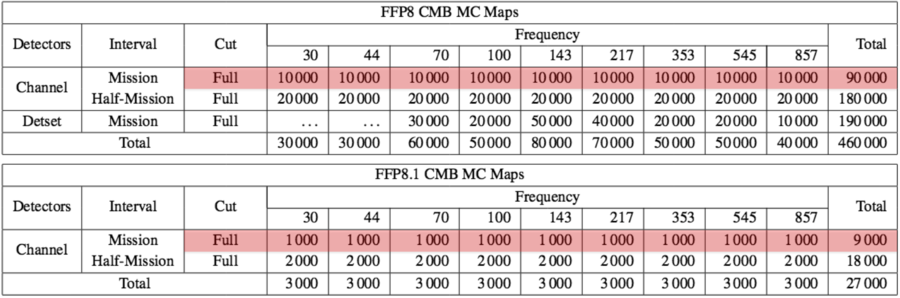
| + | The first two types of simulations, CMB and noise, that are only partially available in the PLA, and the sky simulated maps, have been highlighted in red in Table 1. | ||
| + | |||
| + | The full set of Planck simulations can be found in the NERSC supercomputing center. Instructions on how to access and retrieve the data can be found in [http://crd.lbl.gov/departments/computational-science/c3/c3-research/cosmic-microwave-background/cmb-data-at-nersc/ HERE]. | ||
| + | |||
| + | They contain the dominant instrumental (detector beam, bandpass, and correlated noise properties), scanning (pointing and flags), and analysis (map-making algorithm and implementation) effects. These simulations have been described in {{PlanckPapers|planck2014-a14}}. | ||
| + | |||
| + | In addition to the baseline maps made from the data from all detectors at a given frequency for the entire mission, there are a number of data cuts that are mapped both for systematics tests and to support cross-spectral analyses. These include: | ||
| + | |||
| + | * '''detector subsets''' (“detsets”), comprising the individual unpolarized detectors and the polarized detector quadruplets corresponding to each leading trailing horn pair. Note that HFI sometimes refers to full channels as detset0; here detset only refers to subsets of detectors. | ||
| + | * '''mission subsets''', comprising the surveys, years, and half-missions, with exact boundary definitions given in {{PlanckPapers|planck2014-a03}} and {{PlanckPapers|planck2014-a08}} for LFI and HFI, respectively. | ||
| + | * '''half-ring subsets''', comprising the data from either the first or the second half of each pointing-period ring | ||
| + | |||
| + | The various combinations of these data cuts then define 1134 maps, as enumerated in the top section of Table 1 from {{PlanckPapers|planck2014-a14}}. The different types of map are then named according to their included detectors (channel or detset), interval (mission, half-mission, year or survey), and ring-content (full or half-ring); for example the baseline maps are described as channel/mission/full, etc. | ||
| + | |||
| + | The simulation process consists of | ||
| + | * modelling each astrophysical component of the sky emission for each Planck detector, using Planck data and the relevant characteristics of the Planck instruments. | ||
| + | * simulating each detector's observation of each sky component following the Planck scanning strategy and using the best estimates of the detector's beam and noise properties (obtained in flight), then combining these timelines into a single one per detector, and projecting these simulated timelines onto ''observed'' maps (the ''fiducial'' sky), as is done with the on-orbit data; | ||
| + | * generating Monte Carlo realizations of the CMB and of the noise, again following the Planck scanning strategy and using our best estimates of the detector beams and noise properties respectively. | ||
The first step is performed by the ''Planck Sky Model'' (PSM), and the last two by the ''Planck Simulation Tools'' (PST), both of which are described in the sections below. | The first step is performed by the ''Planck Sky Model'' (PSM), and the last two by the ''Planck Simulation Tools'' (PST), both of which are described in the sections below. | ||
| − | The production of a full focal plane (FFP) simulation, and including the many MC realizations of the CMB and the noise, requires both HFI and LFI data and includes large, computationally challenging, MC realizations. They are too large to be generated on either of the DPC's own cluster. Instead the PST consists of three distinct tools, each designed to run on the largest available supercomputers, that are used to generate the fiducial sky realization, the CMB MC, and the noise MC respectively. The simulations delivered here are part of the | + | The production of a full focal plane (FFP) simulation, and including the many MC realizations of the CMB and the noise, requires both HFI and LFI data and includes large, computationally challenging, MC realizations. They are too large to be generated on either of the DPC's own cluster. Instead the PST consists of three distinct tools, each designed to run on the largest available supercomputers, that are used to generate the fiducial sky realization, the CMB MC, and the noise MC respectively. The simulations delivered here are part of the 8th generation FFP simulations, known as FFP8. They were primarily generated on the National Energy Research Scientific Computing Center (NERSC) in the USA and at CSC–IT Center for Science (CSC) in Finland. |
| + | |||
| + | The fiducial realizations include instrument noise, astrophysical foregrounds, and the lensed scalar, tensor, and non-Gaussian CMB components, and are primarily designed to support the validation and verification of analysis codes. To test our ability to detect tensor modes and non-Gaussianity, we generate five CMB realizations with various cosmologically interesting — but undeclared — values of the tensor-to-scalar ratio '''r''' and non-Gaussianity parameter '''f<sub>NL</sub>'''. To investigate the impact of differences in the bandpasses of the detectors at any given frequency, the foreground sky is simulated using both the individual detector bandpasses and a common average bandpass, to include and exclude the effects of bandpass mismatch. To check that the PR2-2015 results are not sensitive to the exact cosmological parameters used in FFP8 we subsequently generated FFP8.1, exactly matching the PR2-2015 cosmology. | ||
| + | |||
| + | Table 1 of {{PlanckPapers|planck2014-a14}}. The numbers of fiducial, MC noise and MC CMB maps at each frequency by detector subset, data interval, and data cut. | ||
| + | |||
| + | [[File:A14_Table1_1_col.png|center|900px]] | ||
| + | [[File:A14_Table1_2_col.png|center|900px]] | ||
| + | [[File:A14_Table1_3_col.png|center|900px]] | ||
| + | |||
| + | Since mapmaking is a linear operation, the easiest way to generate all of these different realizations is to build the full set of maps of each of six components: | ||
| + | |||
| + | # the lensed scalar CMB (''cmb_scl''); | ||
| + | # the tensor CMB (''cmb_ten''); | ||
| + | # the non-Gaussian complement CMB (''cmb_ngc''); | ||
| + | # the forgreounds including bandpass mismatch (''fg_bpm''); | ||
| + | # the foregrounds excluding bandpass mismatch (''fg_nobpm''); | ||
| + | # the noise. | ||
| + | |||
| + | We then sum these, weighting the tensor and non-Gaussian complement maps with <math>\sqrt{r}</math> and f<sub>NL</sub>, respectively, and including one of the two foreground maps, to produce 10 total maps of each type. The complete fiducial data set then comprises 18,144 maps. | ||
| + | |||
| + | While the full set of maps can be generated for the fiducial cases, for the 10<sup>4</sup>-realization MC sets this would result in some 10<sup>7</sup> maps and require about 6 PB of storage. Instead, therefore, the number of realizations generated for each type of map is chosen to balance the improved statistics it supports against the computational cost of its generation and storage. The remaining noise MCs sample broadly across all data cuts, while the additional CMB MCs are focused on the channel/half-mission/full maps and the subset of the detset/mission/full maps required by the "commander" component separation code {{PlanckPapers|planck2014-a12}}. | ||
| + | |||
| + | == Mission and instrument characteristics == | ||
| + | The goal of FFP8 is to simulate the Planck mission as accurately as possible; however, there are a number of known systematic effects that are not included, either because they are removed in the pre-processing of the time-ordered data (TOD), or because they are insufficiently well-characterized to simulate reliably, or because their inclusion (simulation and removal) would be too computationally expensive. These systematic effects are discussed in detail in {{PlanckPapers|planck2014-a03}} and {{PlanckPapers|planck2014-a08}} and include: | ||
| + | * cosmic ray glitches (HFI); | ||
| + | * spurious spectral lines from the 4-K cooler electronics (HFI); | ||
| + | * non-linearity in the analogue-to-digital converter (HFI); | ||
| + | * imperfect reconstruction of the focal plane geometry. | ||
| + | |||
| + | Note that if the residuals from the treatment of any of these effects could be mapped in isolation, then maps of such systematics could simply be added to the existing FFP8 maps to improve their correspondence to the real data. | ||
| + | |||
| + | === Pointing === | ||
| + | The FFP8 detector pointing is calculated by interpolating the satellite attitude to the detector sample times and by applying a fixed rotation from the satellite frame into the detector frame. The fixed rotations are determined by the measured focal plane geometry as shown in {{PlanckPapers|planck2014-a05}} and {{PlanckPapers|planck2014-a08}}, while the satellite attitude is described in the Planck attitude history files (AHF). The FFP pointing expansion reproduces the DPC pointing to sub-arcsecond accuracy, except for three short and isolated instances during Surveys 6—8 where the LFI sampling frequency was out of specification. Pixelization of the information causes the pointing error to be quantized to either zero (majority of cases) or the distance between pixel centres (3.4' and 1.7' for LFI and HFI, respectively). Since we need a single reconstruction that will serve both instruments efficiently in a massively parallel environment, we use the pointing provided by the Time Ordered Astrophysics Scalable Tools (Toast) package. | ||
| + | |||
| + | === Noise === | ||
| + | We require simulated noise realizations that are representative of the noise in the flight data, including variations in the noise power spectral density (PSD) of each detector over time. To obtain these we developed a noise estimation pipeline complementary to those of the DPCs. The goal of DPC noise estimation is to monitor instrument health and to derive optimal noise weighting, whereas our estimation is optimized to feed into noise simulation. Key features are the use of full mission maps for signal subtraction, long (about 24 hour) realization length, and the use of auto-correlation functions in place of Fourier transforms to handle flagged and masked data (HFI). | ||
| + | |||
| + | === Beams === | ||
| + | The simulations use the so-called scanning beams (e.g., {{PlanckPapers|planck2013-p03}}), which give the point-spread function of for a given detector including all temporal data processing effects: sample integration, demodulation, ADC non-linearity residuals, bolometric time constant residuals, etc. In the absence of significant residuals (LFI), the scanning beams may be estimated from the optical beams by smearing them in the scanning direction to match the finite integration time for each instrument sample. Where there are unknown residuals in the timelines (HFI), the scanning beam must be measured directly from observations of strong point-like sources, namely planets. If the residuals are present but understood, it is possible to simulate the beam measurement and predict the scanning beam shape starting from the optical beam. | ||
| + | |||
| + | For FFP8, the scanning beams are expanded in terms of their spherical harmonic coefficients, <math>b_{\ell m}</math>, with the order of the expansion (maximum <math>\ell</math> and m considered) representing a trade-off between the accuracy of the representation and the computational cost of its convolution. The LFI horns have larger beams with larger sidelobes (due to their location on the outside of the focal plane), and we treat them as full <math>4\pi</math> beams divided into main (up to 1.9°, 1.3°, and 0.9° for 30, 44, and 70 GHz, respectively), intermediate (up to 5°), and sidelobe (above 5°) components {{PlanckPapers|planck2014-a05}}. This division allows us to tune the expansion orders of the three components separately. HFI horns are limited to the main beam component, measured out to 100 arc minutes {{PlanckPapers|planck2014-a08}}. Since detector beams are characterized independently, the simulations naturally include differential beam and pointing systematics. | ||
| − | + | === Bandpasses === | |
| − | + | Both the LFI and HFI detector bandpasses are based on ground measurements (see {{PlanckPapers|planck2013-p03d}}, respectively), although flight data processing for LFI now uses in-flight top-hat approximations rather than the ground measurements that were found to contain systematic errors. Differences in the bandpasses of detectors nominally at the same frequency (the so-called bandpass mismatch) generate spurious signals in the maps, since each detector is seeing a slightly different sky while the mapmaking algorithms assume that the signal in a pixel is the same for all detectors. To quantify the effect of these residuals, in FFP8 we generate detector timelines from foreground maps in two ways, one that incorporates the individual detector bandpasses, the other using an average bandpass for all the detectors at a given frequency. | |
| − | |||
| − | |||
| − | |||
| − | |||
| + | This effect of the bandpass mismatch can be roughly measured from either flight or simulated data using so-called spurious component mapmaking, which provides noisy all-sky estimates of the observed sky differences (the spurious maps), excluding polarization, between individual detectors and the frequency average. We compare the amount of simulated bandpass mismatch to flight data. The spurious component approach is detailed in the Appendix of {{PlanckPapers|planck2014-a14}}. Mismatch between FFP8 and flight data is driven by inaccurate bandpass description (LFI) and incomplete line emission simulation (HFI). The noisy pixels that align with the Planck scanning rings in the HFI maps are regions where the spurious map solution is degenerate with polarization due to insufficient observation orientations. | ||
== The Planck Sky Model == | == The Planck Sky Model == | ||
| − | |||
| − | === | + | The Planck Sky Model, PSM, consists of a set of data and of code used to simulate sky emission at millimeter-wave frequencies; it is described in detail in Delabrouille et al., (2013){{BibCite|delabrouille2012}}, henceforth the PSM paper. |
| + | |||
| + | The Planck Sky Model is available here: | ||
| + | http://www.apc.univ-paris7.fr/~delabrou/PSM/psm.html | ||
| + | |||
| + | The main simulations used to test and validate the Planck data analysis pipelines (and, in particular, component separation) makes use of simulations generated with version 1.9 of the PSM software. The total sky emission is built from the CMB plus ten foreground components, namely thermal dust, spinning dust, synchrotron, CO lines, free-free, thermal Sunyaev-Zel'dovich (SZ) effect (with first order relativistic corrections), kinetic SZ effect, radio and infrared sources, Cosmic Infrared Background (CIB). | ||
| + | |||
| + | The CMB is modelled using [http://camb.info CAMB]. It is based on adiabatic initial perturbations, with the following cosmological parameters as listed in Table 3 of {{PlanckPapers|planck2014-a08}} | ||
| + | |||
| + | [[File:A14_Table3_CosmoParams.png|center|800px]] | ||
| + | |||
| + | === Galactic and extragalactic components === | ||
| + | |||
| + | The '''Galactic ISM emission''' comprises five components: thermal dust, spinning dust, synchrotron, free-free, CO lines (the J=1->0, J=2->1, and J=3->2 lines at 115.27, 230.54, and 345.80 GHz, respectively), and plus the cosmic infrared background (CIB), emission from radio sources, and the thermal and kinetic Sunyaev-Zeldovich (SZ) effects. | ||
| + | |||
| + | The '''thermal dust''' emission is modelled using single-frequency template maps of the intensity and polarization, together with a pixel-dependent emission law. For FFP8 the thermal dust emission templates are derived from the Planck 353 GHz observations. This update of the original PSM dust model is necessary to provide a better match to the emission observed by Planck. While one option would be simply to use the dust opacity map obtained in {{PlanckPapers|planck2013-p06b}}, this map still suffers from significant contamination by CIB anisotropies and infrared point sources. Using it as a 353 GHz dust template in simulations would result in an excess of small scale power (from CIB and infrared sources) scaling exactly as thermal dust across frequencies. The resulting component represents correctly neither dust alone (because of an excess of small scale power) nor the sum of dust and infrared sources (because the frequency scaling of the CIB and infrared sources is wrong). For simulation purposes, the main objective is not to have an exact map of the dust, but instead a map that has the right statistical properties. Hence we produce a template dust map at 353 GHz by removing that fraction of the small-scale power that is due to CIB emission, infra-red sources, CMB, and noise. | ||
| + | |||
| + | The '''spinning-dust''' map used for FFP8 simulations is a simple realization of the spinning dust model, post-processed to remove negative values occurring in a few pixels because of the generation of small-scale fluctuations on top of the spinning dust template extracted from WMAP data. | ||
| + | |||
| + | The FFP8 '''synchrotron''' emission is modelled on the basis of the template emission map observed at 408 MHz by Haslam et al. (1982). This template synchrotron map is extrapolated in frequency using a spectral index map corresponding to a simple power law. | ||
| + | |||
| + | The '''free-free''' spectral dependence is modelled in FFP8 by assuming a constant electron temperature <math>T_{e}</math> = 7000 K. Electron-ion interactions in the ionized phase of the ISM produce emission that is in general fainter than both the synchrotron and the thermal dust emission outside of the active star-forming regions in the Galactic plane. The free-free model uses a single template, which is scaled in frequency by a specific emission law. The free-free spectral index is a slowly varying function of frequency and depends only slightly on the local value of the electron temperature. | ||
| + | |||
| + | The '''radio sources''' are modelled in FFP8 in a different way from the pre-launch versions of the PSM. | ||
| + | |||
| + | For '''strong radio sources''' (<math>S_{30}</math> > 0.5 Jy), we use radio sources at 0.84, 1.4, or 4.85 GHz. For sources observed at two of these frequencies, we extrapolate or interpolate to the third frequency assuming the spectral index estimated from two observed. For sources observed at only one frequency, we use differential source counts to obtain the ratio of steep- to flat-spectrum sources in each interval of flux density considered. From this ratio, we assign spectral indices (randomly) to each source within each flux density interval. Fiducial Gaussian spectral index distributions as a function of spectral class are obtained from the literature. These are then adjusted slightly until there is reasonable agreement between the PSM differential counts and the predicted model counts predicted. | ||
| + | |||
| + | For '''faint radio sources''' (<math>S_{30}</math> <= 0.5 Jy), the pre-launch PSM showed a deficit of sources resulting from inhomogeneities in surveys at different depths. We address this issue by constructing a simulated catalogue of sources at 1.4 GHz. We replace the simulated sources by the observed ones, wherever possible. If, however, in any particular pixel, we have a shortfall of observed sources, we make up the deficit with the simulated sources. Every source in this new catalogue is given a model-derived spectral class. We thus assign a spectral index to each source based on the spectral class, and model the spectrum of each source using four power laws. We also assume some steepening of the spectral index with frequency, with fiducial values of the steepening obtained from the literature. | ||
| + | |||
| + | We combine the faint and strong radio source catalogues we constructed and compute the differential source counts on these sources between 0.005 Jy and 1 Jy. Finally we also model the polarization of these radio sources using the measured polarization fractions from the literature; for each simulated source we draw a polarization fraction at random from the list of real sources of the same spectral type. | ||
| + | |||
| + | The '''SZ clusters''' are simulated following the model of Delabrouille, Melin, and Bartlett (DMB) as implemented in the PSM. A catalogue of halos is drawn from a Poisson distribution of the mass function with a limiting mass of M<sub>500,true</sub> > 2x10<sup>13</sup> <math>M_\odot</math>. We use the pressure profile from the literature to model the thermal SZ emission of each halo given its redshift and mass. We determine the cluster temperature and assume that the profiles are isothermal. These steps allow us to compute the first-order thermal relativistic correction and the kinetic SZ effect for each cluster, both of which are included in the simulation. Finally, we inject catalogued clusters following the same model, and remove from the simulation corresponding clusters in each redshift and mass range. Hence the SZ simulation features the majority of known X-ray and optical clusters, and is fully consistent with X-ray scaling laws and observed Planck SZ counts. | ||
| + | |||
| + | The '''CIB''' model used to simulate FFP8 relies on the distribution of individual galaxies in template maps based on the distribution of dark matter at a range of relevant redshifts. We assume the CIB galaxies can be grouped into three different populations (proto-spheroid, spiral, starburst). Within each population, galaxies have the same SED, while the flux density is randomly distributed according to redshift-dependent number counts obtained from JCMT/SCUBA-2 observations and the Planck ERCSC, as well as observations from Herschel-SPIRE and AzTEC/ASTE. We use the Class software to generate dark matter maps at 17 different redshifts between 1 and 5.5. Since the galaxy distribution does not exactly follow the dark matter distribution, we modify the a<sub>lm</sub> coefficients of dark matter anisotropies given by Class. Template maps generated from the a<sub>lm</sub> coefficients are then exponentiated to avoid negative pixels. Galaxies are randomly distributed with a probability of presence proportional to the pixel values of the template maps. One map is generated for each population, at each redshift, and associated with a redshifted SED depending on the population. The emission of these maps (initially at a reference frequency) can be extrapolated to any frequency using the associated redshifted SED. By summing the emission of all maps, we can generate CIB maps at any frequency in the range of validity of our model. | ||
| + | |||
| + | See {{PlanckPapers|planck2014-a14}} and references therein for a very detailed explanation of the procedures to simulate each of the components. | ||
| + | |||
| + | The sky model is simulated at a resolution common to all components by smoothing the maps with an ideal Gaussian beam of FWHM of 4 arcminute. The Healpix [http://healpix.sourceforge.net] pixelization in Galactic coordinates is used for all components, with Nside = 2048 and <math>\ell_{max}</math> = 6000. Sky emission maps are generated by numerically band-integrating the sky model maps (emission law of each component, in each pixel) over the frequency bands both of each detector in the focal plane and — using an average over the detectors at a given frequency — of each channel. The band-integrated maps are essentially observations of the model sky simulated by an ideal noiseless instrument with ideal Gaussian beams of FWHM equal to the resolution of the model sky. | ||
| + | |||
| + | === The CMB Sky === | ||
| + | |||
| + | The CMB sky is simulated in three distinct components, namely lensed scalar, tensor, and non-Gaussian complement. The total CMB sky is then the weighted sum with weights 1, <math>\sqrt{r}</math>, and f_<sub>NL</sub>, respectively. For FFP8, all CMB sky components are produced as spherical harmonic representations of the I, Q, and U skies. | ||
| + | |||
| + | The FFP8 CMB sky is derived from our best estimate of the cosmological parameters available at the time of its generation, namely those from the first Planck data release {{PlanckPapers|planck2013-p01}}, augmented with a judicious choice of reionization parameter <math>\tau</math>, as listed in Table 3 of {{PlanckPapers|planck2014-a14}}. | ||
| + | |||
| + | ===== The scalar CMB sky ===== | ||
| + | |||
| + | The scalar component of the CMB sky is generated including lensing, Rayleigh scattering, and Doppler boosting effects. | ||
| + | |||
| + | * Using the Camb code, we first calculate fiducial unlensed CMB power spectra <math>C_{\ell}^{TT}</math>, <math>C_{\ell}^{EE}</math>, <math>C_{\ell}^{TE}</math>, the lensing potential power spectrum <math>C_{\ell}^{\phi\phi}</math>, and the cross-correlations <math>C_{\ell}^{T\phi}</math> and <math>C_{\ell}^{E\phi}</math>. We then generate Gaussian T, E, and <math>\phi</math> multipoles with the appropriate covariances and cross-correlations using a Cholesky decomposition and three streams of random Gaussian phases. These fields are simulated up to <math>\ell_{max}</math>=5120. | ||
| + | |||
| + | * Add a dipole component to <math>\phi</math> to account for the Doppler aberration due to our motion with respect to the CMB. <span style="color:#ff0000">UPDATE: Note that although it was intended to include this component in this set of simulations, in the end it was not. It will be included in future versions of the simulation pipeline. </span> | ||
| + | |||
| + | * Compute the effect of gravitational lensing on the temperature and polarization fields, using an algorithm similar to LensPix. We use a fast spherical harmonic transform to compute the temperature, polarization, and deflection fields. The unlensed CMB fields T, Q, and U are evaluated on an equicylindrical pixelization (ECP) grid with <math>N_{\theta}=32\,768</math> and <math>N_{\varphi} = 65\,536</math>, while the deflection field is evaluated on a Healpix Nside=2048 grid. We then calculate the "lensed positions for each Nside=2048 Healpix pixel. We then interpolate T, Q, U at the lensed positions using 2-D cubic Lagrange interpolation on the ECP grid. | ||
| + | |||
| + | * Incorporate the frequency-dependent Doppler modulation effect {{PlanckPapers|planck2013-pipaberration}}. | ||
| + | |||
| + | * Evaluate lensed, Doppler boosted <math>T_{\ell m}</math>, <math>E_{\ell m}</math>, and <math>B_{\ell m}</math> up to <math>\ell_{max}=4\,096</math> with a harmonic transform of the Nside=2048 Healpix map of these interpolated T, Q, and U values. | ||
| + | |||
| + | * Add frequency-dependent Rayleigh scattering effects. | ||
| + | |||
| + | * Add a second-order temperature quadrupole. Since the main Planck data processing removes the frequency-independent part{{PlanckPapers|planck2014-a09}}, we simulate only the residual frequency-dependent temperature quadrupole. After subtracting the frequency-independent part, the simulated quadrupole has frequency dependence <math>\propto (b_{\nu}-1)/2</math>, which we calculate using the bandpass-integrated <math>b_{\nu}</math> boost factors given in Table 4 of {{PlanckPapers|planck2014-a14}}. | ||
| − | The | + | ==== The tensor CMB sky ==== |
| + | In addition to the scalar CMB simulations, we also generate a set of CMB skies containing primordial tensor modes. Using the fiducial cosmological parameters of Table 3 of {{PlanckPapers|planck2014-a14}}, we calculate the tensor power spectra <math>C_{\ell}^{TT, {\rm tensor}}</math>, <math>C_{\ell}^{EE, {\rm tensor}}</math>, and <math>C_{\ell}^{BB, {\rm tensor}}</math> using Camb with a primordial tensor-to-scalar power ratio <math>r=0.2</math> at the pivot scale <math>k=0.05\,Mpc^{-1}</math>. We then simulate Gaussian T, E, and B-modes with these power spectra, and convert these to spherical harmonic representations of the corresponding I, Q and U maps. Note that the default r=0.2 means that building the FFP8a-d maps requires rescaling each CMB tensor map by <math>\sqrt{r/0.2}</math> for each of the values of r in Table 2 of {{PlanckPapers|planck2014-a14}}. | ||
| − | The | + | ==== The non-Gaussian CMB sky ==== |
| + | We use a new algorithm to generate simulations of CMB temperature and polarization maps containing primordial non-Gaussianity. Non-Gaussian fields in general have a non-vanishing bispectrum contribution sourced by mode correlations. The bispectrum, the Fourier transform of the 3-point correlation function, can then be characterized as a function of three wavevectors, <math>F(k_1, k_2, k_3)</math>. Depending on the physical mechanism responsible for generating the non-Gaussian signal, it is possible to introduce broad classes of model that are categorized by the dependence of F on the type of triangle formed by the three momenta <math>k_i</math>. Here, we focus on non-Gaussianity of local type, where the bulk of the signal comes from squeezed triangle configurations, <math>k_1 \ll k_2 \approx k_3</math>. This is typically predicted by multi-field inflationary models. See Section 3.3.3 of {{PlanckPapers|planck2014-a14}} for further details on the simulation of this components and references. | ||
| − | + | ==== The FFP8.1 CMB skies ==== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The | + | The FFP8 simulations are an integral part of the analyses used to derive PR2-2015, and so were necessarily generated prior to determining that release's cosmological parameters. As such there is inevitably a mismatch between the FFP8 and the PR2-2015 cosmologies, which we address in two ways. The quick-and-dirty fix is to determine a single rescaling factor that minimizes the difference between the PR1-2013 and PR2-2015 TT power spectra and apply it to all of the FFP8 CMB maps; this number is determined to be 1.0134, and the rescaled maps have been used in several repeat analyses to confirm the robustness of various PR2-2015 results. |
| − | + | More rigorously though, we also generate a second set of CMB realizations based on the PR2-2015 cosmology, dubbed FFP8.1, and perform our reanalyses using these in place of the FFP8 CMB skies in both the fiducial and MC realizations. Table 3 of {{PlanckPapers|planck2014-a14}} lists the cosmological parameters used for FFP8.1 while Table 1 of {{PlanckPapers|planck2014-a14}} enumerates the current status of the FFP8.1 CMB MCs. | |
| − | + | = The Fiducial Sky Simulations= | |
| − | + | The FFP8 fiducial realization is generated in two steps: | |
| + | # Simulation of the full mission TOD for every detector | ||
| + | # Calculation of maps from the various detector subsets, intervals, and data cuts. | ||
| − | + | Simulation of explicit TODs allows us to incorporate each detector's full beam (including its far sidelobes) and unique input sky (including its bandpass). As noted above, the fiducial realization is generated in six separate components — the three CMB components (lensed scalar, tensor, and non-Gaussian complement), two foreground realizations (with and without bandpass mismatch), and noise. The first five of these are simulated as explicit TODs and then mapped, while the noise is generated using the on-the-fly approach described in the noise MC subsection below. | |
| − | + | TOD generation for any detector proceeds by: | |
| + | # Convolving the appropriate sky component with the beam at every point in a uniformly sampled data cube of Euler angle triplets (encoding the pointing and polarization orientation) to produce the "beamskyset". | ||
| + | # Generating the time-ordered data by interpolating over the beamskyset data cube to the exact pointing and polarization orientation of each sample. | ||
| − | + | Previous FFP simulations, including FFP6, accompanying the 2013 Planck data release, used the LevelS software package to do this. However, this required format conversions for the input pointing data and the output time-ordered data, at significant IO and disk space costs. For FFP8 we have therefore embedded the critical parts of these routines into a new code which uses Toast to interface directly with exchange format data. | |
| − | + | All of the FFP8 fiducial maps are produced using Madam/Toast, a Toast port of the Madam generalized destriping code, which allows for destriping with an arbitrary baseline length, with or without a prior on the baseline distribution (or noise filter). Madam is used to produce the official LFI maps, and its destriping parameters can be chosen so that it reproduces the behaviour of Polkapix, the official HFI mapmaking code. Comparison of the official maps and Madam/Toast maps run using exchange data show that mapmaker differences are negligible compared to small differences in pointing and (for HFI) dipole subtraction that do not impact the simulation. The sky components are mapped from the TODs, while the fiducial noise is taken to be realization 10000 of the noise MC (with realizations 0000-9999 reserved for the noise MC itself). | |
| − | + | Summarizing the key differences in the map making parameters for each Planck frequency: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * 30 GHz is destriped with 0.25 s baselines; 44 and 70 GHz are destriped using 1 s baselines; and 100—857 GHz are destriped using pointing-period baselines (30-75 min). | |
| − | * | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | * 30—70 GHz are destriped with a 1/f-shape noise prior, while 100—857 GHz are destriped without a noise prior. | ||
| − | + | * 30, 44, and 70 GHz have separate destriping masks, while 100—857 GHz use the same 15% galaxy + point source mask. | |
| + | |||
| + | * 30—70 GHz maps are destriped using baselines derived exclusively from the data going into the particular map, while 100-857 GHz maps are destriped using baselines derived from the full data set. | ||
| + | |||
| + | == Noise MC == | ||
| + | |||
| + | The FFP8 noise MCs are generated using Madam/Toast, exploiting Toast's on-the-fly noise simulation capability to avoid the IO overhead of writing a simulated TOD to disk only to read it back in to map it. In this implementation, Madam runs exactly as it would with real data, but whenever it submits a request to Toast to provide it with the an interval of the noise TOD, that interval is simply simulated by Toast in accordance with the noise power spectral densities provided in the runconfig, and returned to Madam. | ||
| + | |||
| + | For a simulation set of this size and complexity, requiring of the order of <math>10^{17}</math> random numbers over <math>10^{12}</math> disjoint and uncorrelated intervals, care must be take with the pseudo-random number generation to ensure that it is fast, reliable (and specifically uncorrelated), and reproducible, in particular enabling any process to generate any element of any subsequence on demand. To achieve this Toast uses a Combined Multiple Recursive Generator (CMRG) that provides more than sufficient period, excellent statistical robustness, and the ability to skip ahead to an arbitrary point in the pseudo-random sequence very quickly. See {{PlanckPapers|planck2014-a14}} for further details on the Noise MCs. | ||
| + | |||
| + | == CMB MC == | ||
| + | |||
| + | The FFP8 CMB MCs are generated using the Febecop software package, which produces beam-convolved maps directly in the pixel domain rather than sample-by-sample, as is done for the fiducial maps. The goal of this approach is to reduce the computational cost by the ratio of time-samples to map-pixels (i.e., the number of hits per pixel). | ||
| + | |||
| + | The Febecop software package proceeds as follows: | ||
| + | |||
| + | # Given the satellite pointing and flags and the focal plane (accessed through the Toast interface), for every channel Febecop first re-orders all of the samples in the mission by pixel instead of time, localizing all of the observations of each pixel, and writes the resulting pixel-ordered detector dngles (PODA) to disk. Note that since the PODA also contains the detector, time-stamp, and weight of each observation this is a one-time operation for each frequency, and does not need to be re-run for different time intervals or detector subsets, or for changes in the beam model or its chosen cut-off radius. | ||
| + | |||
| + | # For every time interval and detector subset to be mapped, and for every pixel in the map, Febecop uses the PODA and the scanning beams to generate an effective-beam for that pixel which is essentially the weighted average of the discretized beam functions for every sample in the pixel included in the time interval and detector subset. The total effective-beam array is also written to disk. Given the PODA, this is a one-time operation for any beam definition. | ||
| + | |||
| + | # Finally, Febecop applies the effective-beam pixel-by-pixel to every CMB sky realization in the MC set to generate the corresponding beam-convolved CMB map realization. | ||
| + | |||
| + | The effective-beams provide a direct connection between the true and observed sky, explicitly incorporating the detailed pointing for every detector through a linear convolution. By providing the effective-beams at every pixel, Febecop enables precise control of systematic effects, e.g., the point-spread functions can be fitted at each pixel on the sky and used to determine point source fluxes {{PlanckPapers|planck2014-a35}} and {{PlanckPapers|planck2014-a36}} | ||
| + | |||
| + | == Validation == | ||
| + | Our goal for the FFP8 simulation set is that it be not only internally self-consistent, but also a good representation of the real data. In addition to the validation steps carried out on all of the inputs individually and noted in their respective sections above, we must also validate the final outputs. A first crude level of validation is provided simply by visual inspection of the FFP8 and real Planck maps where the only immediately apparent difference is the CMB realization. | ||
| + | |||
| + | While this is a necessary test, it is hardly sufficient, and the next step is to compare the angular power spectra of the simulated and real channel/mission/full maps. As illustrated in {{PlanckPapers|planck2014-a35}}, LFI channels show excellent agreement across all angular scales, while HFI channels show a significant power deficit at almost all angular scales. Since this missing HFI power is not picked up in the noise estimation, it must be sky-synchronous (frequency bins corresponding to sky-synchronous signals being discarded when fitting the noise PSDs due to their contamination by signal residuals). This is now understood to be a systematic effect introduced in the HFI pre-processing pipeline, and we are working both to incorporate it as a systematic component in existing simulations and to ameliorate if for future data releases. | ||
| + | |||
| + | Finally, the various analyses of the FFP8 maps in conjunction with the flight data provide powerful incidental validation. To date the only issues observed here are the known mismatch between the FFP8 and PR2-2015 cosmologies, and the missing systematic component in the HFI maps. As noted above, the former is readily addressed by rescaling or using FFP8.1; however, the characterization and reproduction of the latter is an ongoing effort. Specific details of the consequences of this as-yet unresolved issue, such as its impact on null-test failures and ''p''-value stability in studies of non-Gaussianity. In addition, as stated above, the CMB simulations containing only the modulation but not aberration part of the Doppler boost signal. | ||
| + | |||
| + | = Delivered products = | ||
| + | |||
| + | == Fiducial Sky == | ||
| + | |||
| + | There are 9 PSM simulations of the fiducial sky that can be downloaded from the PLA or directly here: | ||
| + | |||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-030_1024_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-044_1024_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-070_1024_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-100_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-143_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-217_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-353_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-545_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-857_2048_R2.00_full.fits | ||
| + | |||
| + | In addition, a set of 9 simulations of the fiducial sky corrected for bandpass mismatch (nobpm) can be obtained here: | ||
| + | |||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-030_1024_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-044_1024_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-070_1024_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-100_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-143_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-217_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-353_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-545_2048_R2.00_full.fits | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-857_2048_R2.00_full.fits | ||
| − | |||
{| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" width=800px | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" width=800px | ||
| − | |+ ''' | + | |+ '''Sky simulated maps file data structure''' |
|- bgcolor="ffdead" | |- bgcolor="ffdead" | ||
| − | !colspan="4" | 1. EXTNAME = ' | + | !colspan="4" | 1. EXTNAME = 'SimMap_Sky' : Data columns |
|- bgcolor="ffdead" | |- bgcolor="ffdead" | ||
! Column Name || Data Type || Units || Description | ! Column Name || Data Type || Units || Description | ||
|- | |- | ||
| − | | | + | |TEMPERATURE || Real*4 || K_cmb (30-353 GHz) or MJy/sr (545 and 857 GHz) || The Stokes I map |
| + | |- | ||
| + | |Q-POLARISATION || Real*4 || K_cmb (30-353 GHz) || The Stokes Q map (optional) | ||
| + | |- | ||
| + | |U-POLARISATION || Real*4 || K_cmb (30-353 GHz) || The Stokes U map (optional) | ||
| + | |- | ||
| + | |- bgcolor="ffdead" | ||
| + | ! Keyword || Data Type || Value || Description | ||
| + | |- | ||
| + | |PIXTYPE || string || HEALPIX || | ||
| + | |- | ||
| + | |COORDSYS || string || GALACTIC ||Coordinate system | ||
| + | |- | ||
| + | |ORDERING || string || NESTED || Healpix ordering | ||
|- | |- | ||
| − | | | + | |POLCCONV || String || COSMO || Polarization convention |
|- | |- | ||
| − | | | + | |NSIDE || Int || 1024 or 2048 || Healpix <math>N_{side}</math> |
|- | |- | ||
| − | | | + | |FIRSTPIX || Int*4 || 0 || First pixel number |
|- | |- | ||
| − | | | + | |LASTPIX || Int*4 || 12 <math>N_{side}</math><sup>2</sup> – 1 || Last pixel number |
|- | |- | ||
| − | | | + | |} |
| + | |||
| + | Note: Original PSM foreground components has been generated at NSIDE 2048 and using a gaussian beam of 4 arcmin. LFI CMB maps has been downgraded at NSIDE 1024. | ||
| + | |||
| + | == CMB MC == | ||
| + | |||
| + | There are 1000 realizations of the lensed CMB per frequency for FFP8 and FFP9, making a total of 18000 CMB simulations available in the PLA. They are named: | ||
| + | |||
| + | * ''HFI_SimMap_cmb-ffp8-scl-{nnnn}_2048_R2.00_nominal.fits'' | ||
| + | * ''LFI_SimMap_cmb-ffp8-scl-{nnnn}_1024_R2.00_nominal.fits'' | ||
| + | |||
| + | * ''HFI_SimMap_cmb-ffp9-scl-{nnnn}_2048_R2.00_nominal.fits'' | ||
| + | * ''LFI_SimMap_cmb-ffp9-scl-{nnnn}_1024_R2.00_nominal.fits'' | ||
| + | |||
| + | where ''nnnn'' ranges from 0000 to 1000. | ||
| + | |||
| + | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" width=800px | ||
| + | |+ '''CMB FFP8 and FFP9 simulated maps file data structure''' | ||
| + | |- bgcolor="ffdead" | ||
| + | !colspan="4" | 1. EXTNAME = 'SimMap_cmb-ffp?-scl' : Data columns | ||
|- bgcolor="ffdead" | |- bgcolor="ffdead" | ||
| − | ! | + | ! Column Name || Data Type || Units || Description |
| + | |- | ||
| + | |TEMPERATURE || Real*4 || K_cmb (30-353 GHz) or MJy/sr (545 and 857 GHz) || The Stokes I map | ||
|- | |- | ||
| − | | | + | |Q-POLARISATION || Real*4 || K_cmb (30-353 GHz) || The Stokes Q map (optional) |
|- | |- | ||
| − | | | + | |U-POLARISATION || Real*4 || K_cmb (30-353 GHz) || The Stokes U map (optional) |
|- | |- | ||
| − | | | + | |- bgcolor="ffdead" |
| + | ! Keyword || Data Type || Value || Description | ||
|- | |- | ||
| − | | | + | |PIXTYPE || string || HEALPIX || |
|- | |- | ||
| − | | | + | |COORDSYS || string || GALACTIC ||Coordinate system |
|- | |- | ||
| − | | | + | |ORDERING || string || RING || Healpix ordering |
|- | |- | ||
| − | | | + | |POLCCONV || String || COSMO || Polarization convention |
|- | |- | ||
| − | | | + | |NSIDE || Int || 1024 or 2048 || Healpix <math>N_{side}</math> |
|- | |- | ||
| − | | | + | |FIRSTPIX || Int*4 || 0 || First pixel number |
|- | |- | ||
| − | | | + | |LASTPIX || Int*4 || 12 <math>N_{side}</math><sup>2</sup> – 1 || Last pixel number |
|- | |- | ||
| − | |||
|} | |} | ||
| − | == | + | == Noise MC == |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | There are 1000 of the noise per frequency for FFP8, making 9000 noise realizations available in the PLA. They are named | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | * ''HFI_SimMap_noise-ffp8-{nnnn}_2048_R2.00_nominal.fits'' | |
| + | * ''LFI_SimMap_noise-ffp8-{nnnn}_1024_R2.00_nominal.fits'' | ||
| − | + | where ''nnnn'' ranges from 0000 to 1000. | |
| − | |||
{| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" width=800px | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" width=800px | ||
| + | |+ '''Noise simulated maps file data structure''' | ||
| + | |- bgcolor="ffdead" | ||
| + | !colspan="4" | 1. EXTNAME = 'SimMap_Sky' : Data columns | ||
| + | |- bgcolor="ffdead" | ||
| + | ! Column Name || Data Type || Units || Description | ||
|- | |- | ||
| − | | | + | |TEMPERATURE || Real*4 || K_cmb || |
|- | |- | ||
| − | | | + | |- bgcolor="ffdead" |
| + | ! Keyword || Data Type || Value || Description | ||
| + | |- | ||
| + | |PIXTYPE || string || HEALPIX || | ||
| + | |- | ||
| + | |COORDSYS || string || GALACTIC ||Coordinate system | ||
| + | |- | ||
| + | |ORDERING || string || NESTED || Healpix ordering | ||
| + | |- | ||
| + | |POLCCONV || String || COSMO || Polarization convention | ||
|- | |- | ||
| − | | | + | |NSIDE || Int || 1024 or 2048 || Healpix <math>N_{side}</math> |
|- | |- | ||
| − | | | + | |FIRSTPIX || Int*4 || 0 || First pixel number |
|- | |- | ||
| − | | | + | |LASTPIX || Int*4 || 12 <math>N_{side}</math><sup>2</sup> – 1 || Last pixel number |
|- | |- | ||
| − | |||
|} | |} | ||
| − | |||
| − | + | = Lensing Simulations = | |
| − | + | ||
| − | + | The lensing simulations package contains 100 realisations of the Planck "MV (TT+TE+ET+TB+BT+EE+EB+BE)" lensing potential estimate (November 2014 pipeline v12), as well as the input lensing realizations. They can be used to determine error bars as well eas effective normalizations for cross-correlation with other tracers of lensing. These simulations are of the lensing convergence map contained in the [[Specially processed maps#Lensing map | Lensing map]] release file. The production and characterisation of this lensing potential map are described in detail in {{PlanckPapers|planck2014-a17}}, which also describes the procedure used to generate the realizations given here. | |
| − | + | ||
| − | |||
| − | + | The simulations are delivered as a gzipped tarball of approximately 8 GB in size. For delivery purposes, the package has been split into 4 2GB files using the unix command | |
| + | : <tt> split -d -b 2048m </tt> | ||
| − | = | + | * http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.00 |
| − | ------ | + | * http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.01 |
| + | * http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.02 | ||
| + | * http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.03 | ||
| − | + | After downloading the individual chunks, the full tarball can be reconstructed with the command | |
| + | : <tt>cat COM_Lensing-SimMap_2048_R2.00.tar.* | tar xvf - </tt> | ||
| − | The | + | The contents of the tarball are described below: |
| − | === | + | {| border="1" cellpadding="3" cellspacing="0" align="center" style="text-align:left" |
| + | |+ ''' Contents of COM_Lensing-SimMap_2048_R2.00.tar ''' | ||
| + | |- bgcolor="ffdead" | ||
| + | ! Filename || Format || Description | ||
| + | |- | ||
| + | | obs_klms/sim_????_klm.fits || HEALPIX FITS format alm, with <math> L_{\rm max} = 2048 </math> || Contains the simulated convergence estimate <math> \hat{\kappa}_{LM} = \frac{1}{2} L(L+1)\hat{\phi}_{LM} </math> for each simulation. | ||
| + | |- | ||
| + | | sky_klms/sim_????_klm.fits || HEALPIX FITS format alm, with <math> L_{\rm max} = 2048 </math> || Contains the input lensing convergence for each simulation. | ||
| + | |- | ||
| + | | inputs/mask.fits.gz || HEALPIX FITS format map, with <math> N_{\rm side} = 2048 </math> || Contains the lens reconstruction analysis mask. | ||
| + | |- | ||
| + | | inputs/cls/cl??.dat || ASCII text file, with columns = (<math>L</math>, <math>C_L </math>) || Contains the fiducial theory CMB power spectra for TT, EE, BB, <math> \kappa \kappa </math> and <math> T \kappa </math>, with temperature and polarization in units of <math> \mu K </math>. | ||
| + | |- | ||
| + | |} | ||
| − | + | = References = | |
| − | |||
| − | |||
| − | |||
| − | + | <References /> | |
| + | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[Category:Mission products|012]] | [[Category:Mission products|012]] | ||
Latest revision as of 12:02, 29 March 2016
Contents
Introduction[edit]
The 2015 Planck data release is supported by a set of simulated maps of the sky, by astrophysical component, and of that sky as seen by Planck (fiducial mission realizations), together with separate sets of Monte Carlo realizations of the CMB and the instrument noise.
Currently, only a subset of these simulations is available from the Planck Legacy Archive. In particular:
- 18000 full mission CMB simulations: 1000 for each of the nine Planck frequencies, and for two different sets of cosmological parameters.
- 9000 full mission noise simulations: 1000 for each of the nine Planck frequencies.
- 18 full mission sky simulated maps: two sets of sky maps with and without bandpass corrections applied.
The first two types of simulations, CMB and noise, that are only partially available in the PLA, and the sky simulated maps, have been highlighted in red in Table 1.
The full set of Planck simulations can be found in the NERSC supercomputing center. Instructions on how to access and retrieve the data can be found in HERE.
They contain the dominant instrumental (detector beam, bandpass, and correlated noise properties), scanning (pointing and flags), and analysis (map-making algorithm and implementation) effects. These simulations have been described in Planck-2015-A12[1].
In addition to the baseline maps made from the data from all detectors at a given frequency for the entire mission, there are a number of data cuts that are mapped both for systematics tests and to support cross-spectral analyses. These include:
- detector subsets (“detsets”), comprising the individual unpolarized detectors and the polarized detector quadruplets corresponding to each leading trailing horn pair. Note that HFI sometimes refers to full channels as detset0; here detset only refers to subsets of detectors.
- mission subsets, comprising the surveys, years, and half-missions, with exact boundary definitions given in Planck-2015-A02[2] and Planck-2015-A07[3] for LFI and HFI, respectively.
- half-ring subsets, comprising the data from either the first or the second half of each pointing-period ring
The various combinations of these data cuts then define 1134 maps, as enumerated in the top section of Table 1 from Planck-2015-A12[1]. The different types of map are then named according to their included detectors (channel or detset), interval (mission, half-mission, year or survey), and ring-content (full or half-ring); for example the baseline maps are described as channel/mission/full, etc.
The simulation process consists of
- modelling each astrophysical component of the sky emission for each Planck detector, using Planck data and the relevant characteristics of the Planck instruments.
- simulating each detector's observation of each sky component following the Planck scanning strategy and using the best estimates of the detector's beam and noise properties (obtained in flight), then combining these timelines into a single one per detector, and projecting these simulated timelines onto observed maps (the fiducial sky), as is done with the on-orbit data;
- generating Monte Carlo realizations of the CMB and of the noise, again following the Planck scanning strategy and using our best estimates of the detector beams and noise properties respectively.
The first step is performed by the Planck Sky Model (PSM), and the last two by the Planck Simulation Tools (PST), both of which are described in the sections below.
The production of a full focal plane (FFP) simulation, and including the many MC realizations of the CMB and the noise, requires both HFI and LFI data and includes large, computationally challenging, MC realizations. They are too large to be generated on either of the DPC's own cluster. Instead the PST consists of three distinct tools, each designed to run on the largest available supercomputers, that are used to generate the fiducial sky realization, the CMB MC, and the noise MC respectively. The simulations delivered here are part of the 8th generation FFP simulations, known as FFP8. They were primarily generated on the National Energy Research Scientific Computing Center (NERSC) in the USA and at CSC–IT Center for Science (CSC) in Finland.
The fiducial realizations include instrument noise, astrophysical foregrounds, and the lensed scalar, tensor, and non-Gaussian CMB components, and are primarily designed to support the validation and verification of analysis codes. To test our ability to detect tensor modes and non-Gaussianity, we generate five CMB realizations with various cosmologically interesting — but undeclared — values of the tensor-to-scalar ratio r and non-Gaussianity parameter fNL. To investigate the impact of differences in the bandpasses of the detectors at any given frequency, the foreground sky is simulated using both the individual detector bandpasses and a common average bandpass, to include and exclude the effects of bandpass mismatch. To check that the PR2-2015 results are not sensitive to the exact cosmological parameters used in FFP8 we subsequently generated FFP8.1, exactly matching the PR2-2015 cosmology.
Table 1 of Planck-2015-A12[1]. The numbers of fiducial, MC noise and MC CMB maps at each frequency by detector subset, data interval, and data cut.
Since mapmaking is a linear operation, the easiest way to generate all of these different realizations is to build the full set of maps of each of six components:
- the lensed scalar CMB (cmb_scl);
- the tensor CMB (cmb_ten);
- the non-Gaussian complement CMB (cmb_ngc);
- the forgreounds including bandpass mismatch (fg_bpm);
- the foregrounds excluding bandpass mismatch (fg_nobpm);
- the noise.
We then sum these, weighting the tensor and non-Gaussian complement maps with and fNL, respectively, and including one of the two foreground maps, to produce 10 total maps of each type. The complete fiducial data set then comprises 18,144 maps.
While the full set of maps can be generated for the fiducial cases, for the 104-realization MC sets this would result in some 107 maps and require about 6 PB of storage. Instead, therefore, the number of realizations generated for each type of map is chosen to balance the improved statistics it supports against the computational cost of its generation and storage. The remaining noise MCs sample broadly across all data cuts, while the additional CMB MCs are focused on the channel/half-mission/full maps and the subset of the detset/mission/full maps required by the "commander" component separation code Planck-2015-A10[4].
Mission and instrument characteristics[edit]
The goal of FFP8 is to simulate the Planck mission as accurately as possible; however, there are a number of known systematic effects that are not included, either because they are removed in the pre-processing of the time-ordered data (TOD), or because they are insufficiently well-characterized to simulate reliably, or because their inclusion (simulation and removal) would be too computationally expensive. These systematic effects are discussed in detail in Planck-2015-A02[2] and Planck-2015-A07[3] and include:
- cosmic ray glitches (HFI);
- spurious spectral lines from the 4-K cooler electronics (HFI);
- non-linearity in the analogue-to-digital converter (HFI);
- imperfect reconstruction of the focal plane geometry.
Note that if the residuals from the treatment of any of these effects could be mapped in isolation, then maps of such systematics could simply be added to the existing FFP8 maps to improve their correspondence to the real data.
Pointing[edit]
The FFP8 detector pointing is calculated by interpolating the satellite attitude to the detector sample times and by applying a fixed rotation from the satellite frame into the detector frame. The fixed rotations are determined by the measured focal plane geometry as shown in Planck-2015-A04[5] and Planck-2015-A07[3], while the satellite attitude is described in the Planck attitude history files (AHF). The FFP pointing expansion reproduces the DPC pointing to sub-arcsecond accuracy, except for three short and isolated instances during Surveys 6—8 where the LFI sampling frequency was out of specification. Pixelization of the information causes the pointing error to be quantized to either zero (majority of cases) or the distance between pixel centres (3.4' and 1.7' for LFI and HFI, respectively). Since we need a single reconstruction that will serve both instruments efficiently in a massively parallel environment, we use the pointing provided by the Time Ordered Astrophysics Scalable Tools (Toast) package.
Noise[edit]
We require simulated noise realizations that are representative of the noise in the flight data, including variations in the noise power spectral density (PSD) of each detector over time. To obtain these we developed a noise estimation pipeline complementary to those of the DPCs. The goal of DPC noise estimation is to monitor instrument health and to derive optimal noise weighting, whereas our estimation is optimized to feed into noise simulation. Key features are the use of full mission maps for signal subtraction, long (about 24 hour) realization length, and the use of auto-correlation functions in place of Fourier transforms to handle flagged and masked data (HFI).
Beams[edit]
The simulations use the so-called scanning beams (e.g., Planck-2013-VI[6]), which give the point-spread function of for a given detector including all temporal data processing effects: sample integration, demodulation, ADC non-linearity residuals, bolometric time constant residuals, etc. In the absence of significant residuals (LFI), the scanning beams may be estimated from the optical beams by smearing them in the scanning direction to match the finite integration time for each instrument sample. Where there are unknown residuals in the timelines (HFI), the scanning beam must be measured directly from observations of strong point-like sources, namely planets. If the residuals are present but understood, it is possible to simulate the beam measurement and predict the scanning beam shape starting from the optical beam.
For FFP8, the scanning beams are expanded in terms of their spherical harmonic coefficients, , with the order of the expansion (maximum and m considered) representing a trade-off between the accuracy of the representation and the computational cost of its convolution. The LFI horns have larger beams with larger sidelobes (due to their location on the outside of the focal plane), and we treat them as full beams divided into main (up to 1.9°, 1.3°, and 0.9° for 30, 44, and 70 GHz, respectively), intermediate (up to 5°), and sidelobe (above 5°) components Planck-2015-A04[5]. This division allows us to tune the expansion orders of the three components separately. HFI horns are limited to the main beam component, measured out to 100 arc minutes Planck-2015-A07[3]. Since detector beams are characterized independently, the simulations naturally include differential beam and pointing systematics.
Bandpasses[edit]
Both the LFI and HFI detector bandpasses are based on ground measurements (see Planck-2013-IX[7], respectively), although flight data processing for LFI now uses in-flight top-hat approximations rather than the ground measurements that were found to contain systematic errors. Differences in the bandpasses of detectors nominally at the same frequency (the so-called bandpass mismatch) generate spurious signals in the maps, since each detector is seeing a slightly different sky while the mapmaking algorithms assume that the signal in a pixel is the same for all detectors. To quantify the effect of these residuals, in FFP8 we generate detector timelines from foreground maps in two ways, one that incorporates the individual detector bandpasses, the other using an average bandpass for all the detectors at a given frequency.
This effect of the bandpass mismatch can be roughly measured from either flight or simulated data using so-called spurious component mapmaking, which provides noisy all-sky estimates of the observed sky differences (the spurious maps), excluding polarization, between individual detectors and the frequency average. We compare the amount of simulated bandpass mismatch to flight data. The spurious component approach is detailed in the Appendix of Planck-2015-A12[1]. Mismatch between FFP8 and flight data is driven by inaccurate bandpass description (LFI) and incomplete line emission simulation (HFI). The noisy pixels that align with the Planck scanning rings in the HFI maps are regions where the spurious map solution is degenerate with polarization due to insufficient observation orientations.
The Planck Sky Model[edit]
The Planck Sky Model, PSM, consists of a set of data and of code used to simulate sky emission at millimeter-wave frequencies; it is described in detail in Delabrouille et al., (2013)[8], henceforth the PSM paper.
The Planck Sky Model is available here: http://www.apc.univ-paris7.fr/~delabrou/PSM/psm.html
The main simulations used to test and validate the Planck data analysis pipelines (and, in particular, component separation) makes use of simulations generated with version 1.9 of the PSM software. The total sky emission is built from the CMB plus ten foreground components, namely thermal dust, spinning dust, synchrotron, CO lines, free-free, thermal Sunyaev-Zel'dovich (SZ) effect (with first order relativistic corrections), kinetic SZ effect, radio and infrared sources, Cosmic Infrared Background (CIB).
The CMB is modelled using CAMB. It is based on adiabatic initial perturbations, with the following cosmological parameters as listed in Table 3 of Planck-2015-A07[3]
Galactic and extragalactic components[edit]
The Galactic ISM emission comprises five components: thermal dust, spinning dust, synchrotron, free-free, CO lines (the J=1->0, J=2->1, and J=3->2 lines at 115.27, 230.54, and 345.80 GHz, respectively), and plus the cosmic infrared background (CIB), emission from radio sources, and the thermal and kinetic Sunyaev-Zeldovich (SZ) effects.
The thermal dust emission is modelled using single-frequency template maps of the intensity and polarization, together with a pixel-dependent emission law. For FFP8 the thermal dust emission templates are derived from the Planck 353 GHz observations. This update of the original PSM dust model is necessary to provide a better match to the emission observed by Planck. While one option would be simply to use the dust opacity map obtained in Planck-2013-XI[9], this map still suffers from significant contamination by CIB anisotropies and infrared point sources. Using it as a 353 GHz dust template in simulations would result in an excess of small scale power (from CIB and infrared sources) scaling exactly as thermal dust across frequencies. The resulting component represents correctly neither dust alone (because of an excess of small scale power) nor the sum of dust and infrared sources (because the frequency scaling of the CIB and infrared sources is wrong). For simulation purposes, the main objective is not to have an exact map of the dust, but instead a map that has the right statistical properties. Hence we produce a template dust map at 353 GHz by removing that fraction of the small-scale power that is due to CIB emission, infra-red sources, CMB, and noise.
The spinning-dust map used for FFP8 simulations is a simple realization of the spinning dust model, post-processed to remove negative values occurring in a few pixels because of the generation of small-scale fluctuations on top of the spinning dust template extracted from WMAP data.
The FFP8 synchrotron emission is modelled on the basis of the template emission map observed at 408 MHz by Haslam et al. (1982). This template synchrotron map is extrapolated in frequency using a spectral index map corresponding to a simple power law.
The free-free spectral dependence is modelled in FFP8 by assuming a constant electron temperature = 7000 K. Electron-ion interactions in the ionized phase of the ISM produce emission that is in general fainter than both the synchrotron and the thermal dust emission outside of the active star-forming regions in the Galactic plane. The free-free model uses a single template, which is scaled in frequency by a specific emission law. The free-free spectral index is a slowly varying function of frequency and depends only slightly on the local value of the electron temperature.
The radio sources are modelled in FFP8 in a different way from the pre-launch versions of the PSM.
For strong radio sources ( > 0.5 Jy), we use radio sources at 0.84, 1.4, or 4.85 GHz. For sources observed at two of these frequencies, we extrapolate or interpolate to the third frequency assuming the spectral index estimated from two observed. For sources observed at only one frequency, we use differential source counts to obtain the ratio of steep- to flat-spectrum sources in each interval of flux density considered. From this ratio, we assign spectral indices (randomly) to each source within each flux density interval. Fiducial Gaussian spectral index distributions as a function of spectral class are obtained from the literature. These are then adjusted slightly until there is reasonable agreement between the PSM differential counts and the predicted model counts predicted.
For faint radio sources ( <= 0.5 Jy), the pre-launch PSM showed a deficit of sources resulting from inhomogeneities in surveys at different depths. We address this issue by constructing a simulated catalogue of sources at 1.4 GHz. We replace the simulated sources by the observed ones, wherever possible. If, however, in any particular pixel, we have a shortfall of observed sources, we make up the deficit with the simulated sources. Every source in this new catalogue is given a model-derived spectral class. We thus assign a spectral index to each source based on the spectral class, and model the spectrum of each source using four power laws. We also assume some steepening of the spectral index with frequency, with fiducial values of the steepening obtained from the literature.
We combine the faint and strong radio source catalogues we constructed and compute the differential source counts on these sources between 0.005 Jy and 1 Jy. Finally we also model the polarization of these radio sources using the measured polarization fractions from the literature; for each simulated source we draw a polarization fraction at random from the list of real sources of the same spectral type.
The SZ clusters are simulated following the model of Delabrouille, Melin, and Bartlett (DMB) as implemented in the PSM. A catalogue of halos is drawn from a Poisson distribution of the mass function with a limiting mass of M500,true > 2x1013. We use the pressure profile from the literature to model the thermal SZ emission of each halo given its redshift and mass. We determine the cluster temperature and assume that the profiles are isothermal. These steps allow us to compute the first-order thermal relativistic correction and the kinetic SZ effect for each cluster, both of which are included in the simulation. Finally, we inject catalogued clusters following the same model, and remove from the simulation corresponding clusters in each redshift and mass range. Hence the SZ simulation features the majority of known X-ray and optical clusters, and is fully consistent with X-ray scaling laws and observed Planck SZ counts.
The CIB model used to simulate FFP8 relies on the distribution of individual galaxies in template maps based on the distribution of dark matter at a range of relevant redshifts. We assume the CIB galaxies can be grouped into three different populations (proto-spheroid, spiral, starburst). Within each population, galaxies have the same SED, while the flux density is randomly distributed according to redshift-dependent number counts obtained from JCMT/SCUBA-2 observations and the Planck ERCSC, as well as observations from Herschel-SPIRE and AzTEC/ASTE. We use the Class software to generate dark matter maps at 17 different redshifts between 1 and 5.5. Since the galaxy distribution does not exactly follow the dark matter distribution, we modify the alm coefficients of dark matter anisotropies given by Class. Template maps generated from the alm coefficients are then exponentiated to avoid negative pixels. Galaxies are randomly distributed with a probability of presence proportional to the pixel values of the template maps. One map is generated for each population, at each redshift, and associated with a redshifted SED depending on the population. The emission of these maps (initially at a reference frequency) can be extrapolated to any frequency using the associated redshifted SED. By summing the emission of all maps, we can generate CIB maps at any frequency in the range of validity of our model.
See Planck-2015-A12[1] and references therein for a very detailed explanation of the procedures to simulate each of the components.
The sky model is simulated at a resolution common to all components by smoothing the maps with an ideal Gaussian beam of FWHM of 4 arcminute. The Healpix [1] pixelization in Galactic coordinates is used for all components, with Nside = 2048 and = 6000. Sky emission maps are generated by numerically band-integrating the sky model maps (emission law of each component, in each pixel) over the frequency bands both of each detector in the focal plane and — using an average over the detectors at a given frequency — of each channel. The band-integrated maps are essentially observations of the model sky simulated by an ideal noiseless instrument with ideal Gaussian beams of FWHM equal to the resolution of the model sky.
The CMB Sky[edit]
The CMB sky is simulated in three distinct components, namely lensed scalar, tensor, and non-Gaussian complement. The total CMB sky is then the weighted sum with weights 1, , and f_NL, respectively. For FFP8, all CMB sky components are produced as spherical harmonic representations of the I, Q, and U skies.
The FFP8 CMB sky is derived from our best estimate of the cosmological parameters available at the time of its generation, namely those from the first Planck data release Planck-2013-I[10], augmented with a judicious choice of reionization parameter , as listed in Table 3 of Planck-2015-A12[1].
The scalar CMB sky[edit]
The scalar component of the CMB sky is generated including lensing, Rayleigh scattering, and Doppler boosting effects.
- Using the Camb code, we first calculate fiducial unlensed CMB power spectra , , , the lensing potential power spectrum , and the cross-correlations and . We then generate Gaussian T, E, and multipoles with the appropriate covariances and cross-correlations using a Cholesky decomposition and three streams of random Gaussian phases. These fields are simulated up to =5120.
- Add a dipole component to to account for the Doppler aberration due to our motion with respect to the CMB. UPDATE: Note that although it was intended to include this component in this set of simulations, in the end it was not. It will be included in future versions of the simulation pipeline.
- Compute the effect of gravitational lensing on the temperature and polarization fields, using an algorithm similar to LensPix. We use a fast spherical harmonic transform to compute the temperature, polarization, and deflection fields. The unlensed CMB fields T, Q, and U are evaluated on an equicylindrical pixelization (ECP) grid with and , while the deflection field is evaluated on a Healpix Nside=2048 grid. We then calculate the "lensed positions for each Nside=2048 Healpix pixel. We then interpolate T, Q, U at the lensed positions using 2-D cubic Lagrange interpolation on the ECP grid.
- Incorporate the frequency-dependent Doppler modulation effect Planck-2013-XXVII[11].
- Evaluate lensed, Doppler boosted , , and up to with a harmonic transform of the Nside=2048 Healpix map of these interpolated T, Q, and U values.
- Add frequency-dependent Rayleigh scattering effects.
- Add a second-order temperature quadrupole. Since the main Planck data processing removes the frequency-independent partPlanck-2015-A08[12], we simulate only the residual frequency-dependent temperature quadrupole. After subtracting the frequency-independent part, the simulated quadrupole has frequency dependence , which we calculate using the bandpass-integrated boost factors given in Table 4 of Planck-2015-A12[1].
The tensor CMB sky[edit]
In addition to the scalar CMB simulations, we also generate a set of CMB skies containing primordial tensor modes. Using the fiducial cosmological parameters of Table 3 of Planck-2015-A12[1], we calculate the tensor power spectra , , and using Camb with a primordial tensor-to-scalar power ratio at the pivot scale . We then simulate Gaussian T, E, and B-modes with these power spectra, and convert these to spherical harmonic representations of the corresponding I, Q and U maps. Note that the default r=0.2 means that building the FFP8a-d maps requires rescaling each CMB tensor map by for each of the values of r in Table 2 of Planck-2015-A12[1].
The non-Gaussian CMB sky[edit]
We use a new algorithm to generate simulations of CMB temperature and polarization maps containing primordial non-Gaussianity. Non-Gaussian fields in general have a non-vanishing bispectrum contribution sourced by mode correlations. The bispectrum, the Fourier transform of the 3-point correlation function, can then be characterized as a function of three wavevectors, . Depending on the physical mechanism responsible for generating the non-Gaussian signal, it is possible to introduce broad classes of model that are categorized by the dependence of F on the type of triangle formed by the three momenta . Here, we focus on non-Gaussianity of local type, where the bulk of the signal comes from squeezed triangle configurations, . This is typically predicted by multi-field inflationary models. See Section 3.3.3 of Planck-2015-A12[1] for further details on the simulation of this components and references.
The FFP8.1 CMB skies[edit]
The FFP8 simulations are an integral part of the analyses used to derive PR2-2015, and so were necessarily generated prior to determining that release's cosmological parameters. As such there is inevitably a mismatch between the FFP8 and the PR2-2015 cosmologies, which we address in two ways. The quick-and-dirty fix is to determine a single rescaling factor that minimizes the difference between the PR1-2013 and PR2-2015 TT power spectra and apply it to all of the FFP8 CMB maps; this number is determined to be 1.0134, and the rescaled maps have been used in several repeat analyses to confirm the robustness of various PR2-2015 results.
More rigorously though, we also generate a second set of CMB realizations based on the PR2-2015 cosmology, dubbed FFP8.1, and perform our reanalyses using these in place of the FFP8 CMB skies in both the fiducial and MC realizations. Table 3 of Planck-2015-A12[1] lists the cosmological parameters used for FFP8.1 while Table 1 of Planck-2015-A12[1] enumerates the current status of the FFP8.1 CMB MCs.
The Fiducial Sky Simulations[edit]
The FFP8 fiducial realization is generated in two steps:
- Simulation of the full mission TOD for every detector
- Calculation of maps from the various detector subsets, intervals, and data cuts.
Simulation of explicit TODs allows us to incorporate each detector's full beam (including its far sidelobes) and unique input sky (including its bandpass). As noted above, the fiducial realization is generated in six separate components — the three CMB components (lensed scalar, tensor, and non-Gaussian complement), two foreground realizations (with and without bandpass mismatch), and noise. The first five of these are simulated as explicit TODs and then mapped, while the noise is generated using the on-the-fly approach described in the noise MC subsection below.
TOD generation for any detector proceeds by:
- Convolving the appropriate sky component with the beam at every point in a uniformly sampled data cube of Euler angle triplets (encoding the pointing and polarization orientation) to produce the "beamskyset".
- Generating the time-ordered data by interpolating over the beamskyset data cube to the exact pointing and polarization orientation of each sample.
Previous FFP simulations, including FFP6, accompanying the 2013 Planck data release, used the LevelS software package to do this. However, this required format conversions for the input pointing data and the output time-ordered data, at significant IO and disk space costs. For FFP8 we have therefore embedded the critical parts of these routines into a new code which uses Toast to interface directly with exchange format data.
All of the FFP8 fiducial maps are produced using Madam/Toast, a Toast port of the Madam generalized destriping code, which allows for destriping with an arbitrary baseline length, with or without a prior on the baseline distribution (or noise filter). Madam is used to produce the official LFI maps, and its destriping parameters can be chosen so that it reproduces the behaviour of Polkapix, the official HFI mapmaking code. Comparison of the official maps and Madam/Toast maps run using exchange data show that mapmaker differences are negligible compared to small differences in pointing and (for HFI) dipole subtraction that do not impact the simulation. The sky components are mapped from the TODs, while the fiducial noise is taken to be realization 10000 of the noise MC (with realizations 0000-9999 reserved for the noise MC itself).
Summarizing the key differences in the map making parameters for each Planck frequency:
- 30 GHz is destriped with 0.25 s baselines; 44 and 70 GHz are destriped using 1 s baselines; and 100—857 GHz are destriped using pointing-period baselines (30-75 min).
- 30—70 GHz are destriped with a 1/f-shape noise prior, while 100—857 GHz are destriped without a noise prior.
- 30, 44, and 70 GHz have separate destriping masks, while 100—857 GHz use the same 15% galaxy + point source mask.
- 30—70 GHz maps are destriped using baselines derived exclusively from the data going into the particular map, while 100-857 GHz maps are destriped using baselines derived from the full data set.
Noise MC[edit]
The FFP8 noise MCs are generated using Madam/Toast, exploiting Toast's on-the-fly noise simulation capability to avoid the IO overhead of writing a simulated TOD to disk only to read it back in to map it. In this implementation, Madam runs exactly as it would with real data, but whenever it submits a request to Toast to provide it with the an interval of the noise TOD, that interval is simply simulated by Toast in accordance with the noise power spectral densities provided in the runconfig, and returned to Madam.
For a simulation set of this size and complexity, requiring of the order of random numbers over disjoint and uncorrelated intervals, care must be take with the pseudo-random number generation to ensure that it is fast, reliable (and specifically uncorrelated), and reproducible, in particular enabling any process to generate any element of any subsequence on demand. To achieve this Toast uses a Combined Multiple Recursive Generator (CMRG) that provides more than sufficient period, excellent statistical robustness, and the ability to skip ahead to an arbitrary point in the pseudo-random sequence very quickly. See Planck-2015-A12[1] for further details on the Noise MCs.
CMB MC[edit]
The FFP8 CMB MCs are generated using the Febecop software package, which produces beam-convolved maps directly in the pixel domain rather than sample-by-sample, as is done for the fiducial maps. The goal of this approach is to reduce the computational cost by the ratio of time-samples to map-pixels (i.e., the number of hits per pixel).
The Febecop software package proceeds as follows:
- Given the satellite pointing and flags and the focal plane (accessed through the Toast interface), for every channel Febecop first re-orders all of the samples in the mission by pixel instead of time, localizing all of the observations of each pixel, and writes the resulting pixel-ordered detector dngles (PODA) to disk. Note that since the PODA also contains the detector, time-stamp, and weight of each observation this is a one-time operation for each frequency, and does not need to be re-run for different time intervals or detector subsets, or for changes in the beam model or its chosen cut-off radius.
- For every time interval and detector subset to be mapped, and for every pixel in the map, Febecop uses the PODA and the scanning beams to generate an effective-beam for that pixel which is essentially the weighted average of the discretized beam functions for every sample in the pixel included in the time interval and detector subset. The total effective-beam array is also written to disk. Given the PODA, this is a one-time operation for any beam definition.
- Finally, Febecop applies the effective-beam pixel-by-pixel to every CMB sky realization in the MC set to generate the corresponding beam-convolved CMB map realization.
The effective-beams provide a direct connection between the true and observed sky, explicitly incorporating the detailed pointing for every detector through a linear convolution. By providing the effective-beams at every pixel, Febecop enables precise control of systematic effects, e.g., the point-spread functions can be fitted at each pixel on the sky and used to determine point source fluxes Planck-2015-A26[13] and Planck-2015-A27[14]
Validation[edit]
Our goal for the FFP8 simulation set is that it be not only internally self-consistent, but also a good representation of the real data. In addition to the validation steps carried out on all of the inputs individually and noted in their respective sections above, we must also validate the final outputs. A first crude level of validation is provided simply by visual inspection of the FFP8 and real Planck maps where the only immediately apparent difference is the CMB realization.
While this is a necessary test, it is hardly sufficient, and the next step is to compare the angular power spectra of the simulated and real channel/mission/full maps. As illustrated in Planck-2015-A26[13], LFI channels show excellent agreement across all angular scales, while HFI channels show a significant power deficit at almost all angular scales. Since this missing HFI power is not picked up in the noise estimation, it must be sky-synchronous (frequency bins corresponding to sky-synchronous signals being discarded when fitting the noise PSDs due to their contamination by signal residuals). This is now understood to be a systematic effect introduced in the HFI pre-processing pipeline, and we are working both to incorporate it as a systematic component in existing simulations and to ameliorate if for future data releases.
Finally, the various analyses of the FFP8 maps in conjunction with the flight data provide powerful incidental validation. To date the only issues observed here are the known mismatch between the FFP8 and PR2-2015 cosmologies, and the missing systematic component in the HFI maps. As noted above, the former is readily addressed by rescaling or using FFP8.1; however, the characterization and reproduction of the latter is an ongoing effort. Specific details of the consequences of this as-yet unresolved issue, such as its impact on null-test failures and p-value stability in studies of non-Gaussianity. In addition, as stated above, the CMB simulations containing only the modulation but not aberration part of the Doppler boost signal.
Delivered products[edit]
Fiducial Sky[edit]
There are 9 PSM simulations of the fiducial sky that can be downloaded from the PLA or directly here:
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-030_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-044_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-070_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-100_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-143_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-217_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-353_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-545_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-bpm-857_2048_R2.00_full.fits
In addition, a set of 9 simulations of the fiducial sky corrected for bandpass mismatch (nobpm) can be obtained here:
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-030_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-044_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-070_1024_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-100_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-143_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-217_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-353_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-545_2048_R2.00_full.fits
- http://pla.esac.esa.int/pla/aio/product-action?SIMULATED_MAP.FILE_ID=COM_SimMap_sky-ffp8-nobpm-857_2048_R2.00_full.fits
| 1. EXTNAME = 'SimMap_Sky' : Data columns | |||
|---|---|---|---|
| Column Name | Data Type | Units | Description |
| TEMPERATURE | Real*4 | K_cmb (30-353 GHz) or MJy/sr (545 and 857 GHz) | The Stokes I map |
| Q-POLARISATION | Real*4 | K_cmb (30-353 GHz) | The Stokes Q map (optional) |
| U-POLARISATION | Real*4 | K_cmb (30-353 GHz) | The Stokes U map (optional) |
| Keyword | Data Type | Value | Description |
| PIXTYPE | string | HEALPIX | |
| COORDSYS | string | GALACTIC | Coordinate system |
| ORDERING | string | NESTED | Healpix ordering |
| POLCCONV | String | COSMO | Polarization convention |
| NSIDE | Int | 1024 or 2048 | Healpix |
| FIRSTPIX | Int*4 | 0 | First pixel number |
| LASTPIX | Int*4 | 12 2 – 1 | Last pixel number |
Note: Original PSM foreground components has been generated at NSIDE 2048 and using a gaussian beam of 4 arcmin. LFI CMB maps has been downgraded at NSIDE 1024.
CMB MC[edit]
There are 1000 realizations of the lensed CMB per frequency for FFP8 and FFP9, making a total of 18000 CMB simulations available in the PLA. They are named:
- HFI_SimMap_cmb-ffp8-scl-{nnnn}_2048_R2.00_nominal.fits
- LFI_SimMap_cmb-ffp8-scl-{nnnn}_1024_R2.00_nominal.fits
- HFI_SimMap_cmb-ffp9-scl-{nnnn}_2048_R2.00_nominal.fits
- LFI_SimMap_cmb-ffp9-scl-{nnnn}_1024_R2.00_nominal.fits
where nnnn ranges from 0000 to 1000.
| 1. EXTNAME = 'SimMap_cmb-ffp?-scl' : Data columns | |||
|---|---|---|---|
| Column Name | Data Type | Units | Description |
| TEMPERATURE | Real*4 | K_cmb (30-353 GHz) or MJy/sr (545 and 857 GHz) | The Stokes I map |
| Q-POLARISATION | Real*4 | K_cmb (30-353 GHz) | The Stokes Q map (optional) |
| U-POLARISATION | Real*4 | K_cmb (30-353 GHz) | The Stokes U map (optional) |
| Keyword | Data Type | Value | Description |
| PIXTYPE | string | HEALPIX | |
| COORDSYS | string | GALACTIC | Coordinate system |
| ORDERING | string | RING | Healpix ordering |
| POLCCONV | String | COSMO | Polarization convention |
| NSIDE | Int | 1024 or 2048 | Healpix |
| FIRSTPIX | Int*4 | 0 | First pixel number |
| LASTPIX | Int*4 | 12 2 – 1 | Last pixel number |
Noise MC[edit]
There are 1000 of the noise per frequency for FFP8, making 9000 noise realizations available in the PLA. They are named
- HFI_SimMap_noise-ffp8-{nnnn}_2048_R2.00_nominal.fits
- LFI_SimMap_noise-ffp8-{nnnn}_1024_R2.00_nominal.fits
where nnnn ranges from 0000 to 1000.
| 1. EXTNAME = 'SimMap_Sky' : Data columns | |||
|---|---|---|---|
| Column Name | Data Type | Units | Description |
| TEMPERATURE | Real*4 | K_cmb | |
| Keyword | Data Type | Value | Description |
| PIXTYPE | string | HEALPIX | |
| COORDSYS | string | GALACTIC | Coordinate system |
| ORDERING | string | NESTED | Healpix ordering |
| POLCCONV | String | COSMO | Polarization convention |
| NSIDE | Int | 1024 or 2048 | Healpix |
| FIRSTPIX | Int*4 | 0 | First pixel number |
| LASTPIX | Int*4 | 12 2 – 1 | Last pixel number |
Lensing Simulations
The lensing simulations package contains 100 realisations of the Planck "MV (TT+TE+ET+TB+BT+EE+EB+BE)" lensing potential estimate (November 2014 pipeline v12), as well as the input lensing realizations. They can be used to determine error bars as well eas effective normalizations for cross-correlation with other tracers of lensing. These simulations are of the lensing convergence map contained in the Lensing map release file. The production and characterisation of this lensing potential map are described in detail in Planck-2015-A15[15], which also describes the procedure used to generate the realizations given here.
The simulations are delivered as a gzipped tarball of approximately 8 GB in size. For delivery purposes, the package has been split into 4 2GB files using the unix command
- split -d -b 2048m
- http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.00
- http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.01
- http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.02
- http://pla.esac.esa.int/pla/aio/product-action?COSMOLOGY.FILE_ID=COM_Lensing-SimMap_2048_R2.00.tar.03
After downloading the individual chunks, the full tarball can be reconstructed with the command
- cat COM_Lensing-SimMap_2048_R2.00.tar.* | tar xvf -
The contents of the tarball are described below:
| Filename | Format | Description |
|---|---|---|
| obs_klms/sim_????_klm.fits | HEALPIX FITS format alm, with | Contains the simulated convergence estimate for each simulation. |
| sky_klms/sim_????_klm.fits | HEALPIX FITS format alm, with | Contains the input lensing convergence for each simulation. |
| inputs/mask.fits.gz | HEALPIX FITS format map, with | Contains the lens reconstruction analysis mask. |
| inputs/cls/cl??.dat | ASCII text file, with columns = (, ) | Contains the fiducial theory CMB power spectra for TT, EE, BB, and , with temperature and polarization in units of . |
References
- ↑ 1.001.011.021.031.041.051.061.071.081.091.101.111.12 Planck 2015 results. XII. Full Focal Plane Simulations, Planck Collaboration, 2016, A&A, 594, A12.
- ↑ 2.02.1 Planck 2015 results. II. LFI processing, Planck Collaboration, 2016, A&A, 594, A2.
- ↑ 3.03.13.23.33.4 Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
- ↑ Planck 2015 results. X. Diffuse component separation: Foreground maps, Planck Collaboration, 2016, A&A, 594, A10.
- ↑ 5.05.1 Planck 2015 results. IV. LFI beams and window functions, Planck Collaboration, 2016, A&A, 594, A4.
- ↑ Planck 2013 results. VI. High Frequency Instrument Data Processing, Planck Collaboration, 2014, A&A, 571, A6
- ↑ Planck 2013 results. IX. HFI spectral response, Planck Collaboration, 2014, A&A, 571, A9
- ↑ The pre-launch Planck Sky Model: a model of sky emission at submillimetre to centimetre wavelengths, J. Delabrouille, M. Betoule, J.-B. Melin, M.-A. Miville-Deschênes, J. Gonzalez-Nuevo, M. Le Jeune, G. Castex, G. de Zotti, S. Basak, M. Ashdown, J. Aumont, C. Baccigalupi, A. Banday, J.-P. Bernard, F. R. Bouchet, D. L. Clements, A. da Silva, C. Dickinson, F. Dodu, K. Dolag, F. Elsner, L. Fauvet, G. Faÿ, G. Giardino, S. Leach, J. Lesgourgues, M. Liguori, J. F. Macias-Perez, M. Massardi, S. Matarrese, P. Mazzotta, L. Montier, S. Mottet, R. Paladini, B. Partridge, R. Piffaretti, G. Prezeau, S. Prunet, S. Ricciardi, M. Roman, B. Schaefer, L. Toffolatti, A&A, 553, A96, (2013).
- ↑ Planck 2013 results. XII. All-sky model of thermal dust emission, Planck Collaboration, 2014, A&A, 571, A12
- ↑ Planck 2013 results. I. Overview of Products and Results, Planck Collaboration, 2014, A&A, 571, A1
- ↑ Planck 2013 results. XXVII. Doppler boosting of the CMB: Eppur si muove, Planck Collaboration, 2014, A&A, 571, A27
- ↑ Planck 2015 results. VIII. High Frequency Instrument data processing: Calibration and maps, Planck Collaboration, 2016, A&A, 594, A8.
- ↑ 13.013.1 Planck 2015 results. XXVI. The second Planck catalogue of compact sources, Planck Collaboration, 2016, A&A, 594, A26.
- ↑ Planck 2015 results. XXVII. The second Planck catalogue of Sunyaev-Zeldovich sources, Planck Collaboration, 2016, A&A, 594, A27.
- ↑ Planck 2015 results. XV. Gravitational Lensing, Planck Collaboration, 2016, A&A, 594, A15.
Cosmic Microwave background
Planck Legacy Archive
(Planck) High Frequency Instrument
(Planck) Low Frequency Instrument
Planck Sky Model
Data Processing Center
Attitude History File
analog to digital converter
Sunyaev-Zel'dovich
Early Release Compact Source Catalog
Full-Width-at-Half-Maximum
Flexible Image Transfer Specification