CMB spectrum and likelihood code
Contents
CMB spectra[edit]
General description[edit]
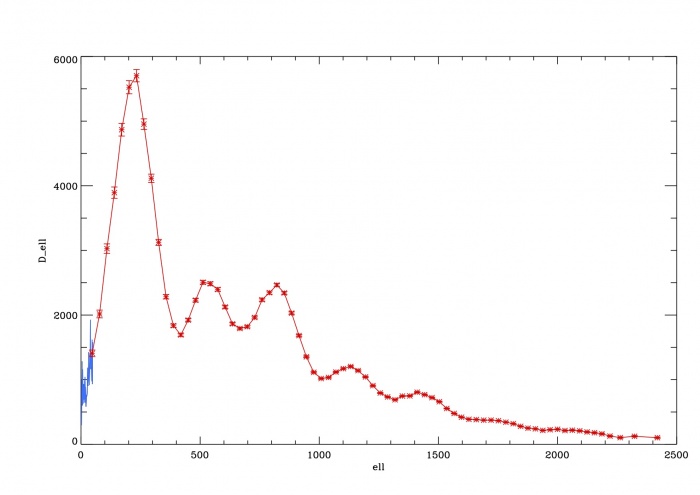
The Planck best-fit CMB temperature power spectrum, shown in figure below, covers the wide range of multipoles = 2-2508. Over the multipole range = 2–29, the power spectrum is derived from a component-separation algorithm, Commander, UPDATE COMMANDER: applied to maps in the frequency range 30–353 GHz over 91% of the sky Planck-2013-XII[1] . The asymmetric error bars associated to this spectrum are the 68% confidence limits and include the uncertainties due to foreground subtraction . For multipoles greater than , instead, the spectrum is derived from the Plik likelihood Planck-2015-A11[2] by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds. Associated 1-sigma errors include beam uncertainties CHECK:and foreground . Both Commander and Plik are described in more details in the sections below.
Production process[edit]
UPDATE COMMANDER The < 50 part of the Planck power spectrum is derived from the Commander approach, which implements Bayesian component separation in pixel space, fitting a parametric model to the data by sampling the posterior distribution for the model parameters Planck-2013-XII[1]. The power spectrum at any multipole is given as the maximum probability point for the posterior distribution, marginalized over the other multipoles, and the error bars are 68% confidence level Planck-2013-XV[4]. The > 30 part of the CMB temperature power spectrum has been derived by the Plik likelihood, a code that implements a pseudo-Cl based technique, extensively described in Sec. 2 and the Appendix of Planck-2013-XV[4]. Frequency spectra are computed as noise weighted averages of the cross-spectra between single detector and sets of detector maps. Mask and multipole range choices for each frequency spectrum are summarized in Table 4 of Planck-2013-XV[4]. The final power spectrum is an optimal combination of the 100, 143, 143x217 and 217 GHz spectra, corrected for the best-fit unresolved foregrounds and inter-frequency calibration factors, as derived from the full likelihood analysis (cf Planck+TT+lowP in Table 3 of [5]). A thorough description of the models of unresolved foregrounds is given in [6] UPDATE SECTION . The spectrum covariance matrix accounts for cosmic variance and noise contributions, together with beam uncertainties. Both spectrum and associated covariance matrix are given as uniformly weighted band averages in 83 bins.
Inputs[edit]
- Low-l spectrum ()
- frequency maps from 30–353 GHz
- common mask Planck-2013-XII[1]
- compact sources catalog
- High-l spectrum ()
- 100, 143, 143x217 and 217 GHz spectra and their covariance matrix (Sec. 2 in Planck-2013-XV[4])
- best-fit foreground templates and inter-frequency calibration factors (Table 5 of Planck-2013-XVI[7])
- Beam transfer function uncertainties Planck-2013-VII[8]
File names and Meta data[edit]
The CMB spectrum and its covariance matrix are distributed in a single FITS file named
which contains 3 extensions
- LOW-ELL (BINTABLE)
- with the low ell part of the spectrum, not binned, and for l=2-49. The table columns are
- ELL (integer): multipole number
- D_ELL (float): $D_l$ as described below
- ERRUP (float): the upward uncertainty
- ERRDOWN (float): the downward uncertainty
- HIGH-ELL (BINTABLE)
- with the high-ell part of the spectrum, binned into 74 bins covering in bins of width (with the exception of the last 4 bins that are wider). The table columns are as follows:
- ELL (integer): mean multipole number of bin
- L_MIN (integer): lowest multipole of bin
- L_MAX (integer): highest multipole of bin
- D_ELL (float): $D_l$ as described below
- ERR (float): the uncertainty
- COV-MAT (IMAGE)
- with the covariance matrix of the high-ell part of the spectrum in a 74x74 pixel image, i.e., covering the same bins as the HIGH-ELL table.
The spectra give $D_\ell = \ell(\ell+1)C_\ell / 2\pi$ in units of $\mu\, K^2$, and the covariance matrix is in units of $\mu\, K^4$. The spectra are shown in the figure below, in blue and red for the low- and high- parts, respectively, and with the error bars for the high-ell part only in order to avoid confusion.
The CMB spectrum is also given in a simple text comma-separated file:
Likelihood[edit]
TO BE WRITTEN.
References[edit]
- ↑ 1.01.11.2 Planck 2013 results. XI. Component separation, Planck Collaboration, 2014, A&A, 571, A11
- ↑ Planck 2015 results. XI. CMB power spectra, likelihoods, and robustness of cosmological parameters, Planck Collaboration, 2016, A&A, 594, A11.
- ↑ Planck 2015 results. XIII. Cosmological parameters, Planck Collaboration, 2016, A&A, 594, A13.
- ↑ 4.04.14.24.3 Planck 2013 results. XV. CMB power spectra and likelihood, Planck Collaboration, 2014, A&A, 571, A15
- ↑
- ↑
- ↑ Planck 2013 results. XVI. Cosmological parameters, Planck Collaboration, 2014, A&A, 571, A16
- ↑ Planck 2013 results. VII. HFI time response and beams, Planck Collaboration, 2014, A&A, 571, A7
Cosmic Microwave background
Flexible Image Transfer Specification