Difference between revisions of "Beams LFI"
(→Sidelobes) |
|||
| Line 59: | Line 59: | ||
== Effective beams == | == Effective beams == | ||
| − | + | The '''effective beam''' is the average of all scanning beams pointing at a certain direction within a given pixel of the sky map for a given scan strategy. It takes into account the coupling between azimuthal asymmetry of the beam and the uneven distribution of scanning angles across the sky. | |
| + | It captures the complete information about the difference between the true and observed image of the sky. They are, by definition, the objects whose convolution with the true CMB sky produce the observed sky map. | ||
| + | |||
| + | The full algebra involving the effective beams for temperature and polarisation was presented in [[http://arxiv.org/pdf/1005.1929| Mitra, Rocha, Gorski et al.]] <cite>#mitra2010</cite>. Here we summarise the main results. The observed temperature sky <math>\widetilde{\mathbf{T}} </math> is a convolution of the true sky <math>\mathbf{T} </math> and the effective beam <math>\mathbf{B}</math>: | ||
| + | |||
| + | <math> | ||
| + | \widetilde{\mathbf{T}} \ = \ \Delta\Omega \, \mathbf{B} \cdot \mathbf{T}, | ||
| + | \label{eq:a0} | ||
| + | </math> | ||
| + | |||
| + | where | ||
| + | |||
| + | <math> | ||
| + | B_{ij} \ = \ \left( \sum_t A_{ti} \, b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) \right) / \left({\sum_t A_{ti}} \right) \, , | ||
| + | \label{eq:EBT2} | ||
| + | </math> | ||
| + | |||
| + | <math>t</math> is time samples, <math>A_{ti}</math> is <math>1</math> if the pointing direction falls in pixel number <math>i</math>, else it is <math>0</math>, <math>\mathbf{p}_t</math> represents the exact pointing direction (not approximated by the pixel centre location), and <math>\hat{\mathbf{r}}_j</math> is the centre of the pixel number <math>j</math>, where the scanbeam <math>b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t)</math> is being evaluated (if the pointing direction falls within the cut-off radius of <math>\sim 2.5 \times</math> FWHM. | ||
| + | |||
| + | The algebra is a bit more involved for polarised detectors. The observed stokes parameters at a pixel <math>i</math>, <math>(\widetilde{I}, \widetilde{Q}, \widetilde{U})_i</math>, are related to the true stokes parameters <math>(I, Q, U)_i</math>, by the following relation: | ||
| + | |||
| + | <math> | ||
| + | ( \widetilde{I} \quad \widetilde{Q} \quad \widetilde{U})_i^T \ = \ \Delta\Omega \sum_j \mathbf{B}_{ij} \cdot (I \quad Q \quad U)_j^T, | ||
| + | \label{eq:a1} | ||
| + | </math> | ||
| + | |||
| + | where the polarised effective beam matrix | ||
| + | |||
| + | <math> | ||
| + | \mathbf{B}_{ij} \ = \ \left[ \sum_t A_{tp} \mathbf{w}_t \mathbf{w}^T_t \right]^{-1} \sum_t A_{ti} \, b(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) \, \mathbf{w}_t \mathbf{W}^T(\hat{\mathbf{n}}_j,\hat{\mathbf{p}}_t) \, , | ||
| + | \label{eq:a2} | ||
| + | </math> | ||
| + | |||
| + | and <math>\mathbf{w}_t </math>and <math>\mathbf{W}(\hat{\mathbf{r}}_j, \hat{\mathbf{p}}_t) </math> are the the polarisation weight vectors, as defined in \cite{mitra2010}. | ||
| + | |||
| + | The task is to compute <math>B_{ij}</math> for temperature only beams and the <math>3 \times 3</math> matrices <math>\mathbf{B}_{ij}</math> for each pixel <math>i</math>, at every neighbouring pixel <math>j</math> that fall within the cut-off radius around the the center of the <math>i^\text{th}</math> pixel. | ||
| + | |||
| + | |||
| + | |||
| + | The effective beam is computed by stacking within a small field around each pixel of the HEALPix sky map. Due to the particular features of Planck scanning strategy coupled to the beam asymmetries in the focal plane, and data processing of the bolometer and radiometer TOIs, the resulting Planck effective beams vary over the sky. | ||
| + | |||
| + | FEBeCoP, given information on Planck scanning beams and detector pointing during a mission period of interest, provides the pixelized stamps of both the Effective Beam, EB, and the Point Spread Function, PSF, at all positions of the HEALPix-formatted map pixel centres. | ||
| + | |||
| + | |||
| + | |||
| + | ===Comparison of the images of compact sources observed by Planck with FEBeCoP products=== | ||
| + | |||
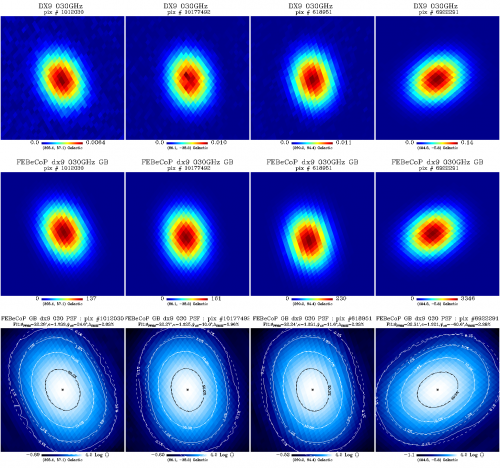
| + | We show here a comparison of the FEBeCoP derived effective beams, and associated point spread functions,PSF (the transpose of the beam matrix), to the actual images of a few compact sources observed by Planck, for 30GHz and 100GHz frequency channels, as an example. We show below a few panels of source images organized as follows: | ||
| + | * Row #1- DX9 images of four ERCSC objects with their galactic (l,b) coordinates shown under the color bar | ||
| + | * Row #2- linear scale FEBeCoP PSFs computed using input scanning beams, Grasp Beams, GB, for LFI and B-Spline beams,BS, Mars12 apodized for the CMB channels and the BS Mars12 for the sub-mm channels, for HFI (see section Inputs below). | ||
| + | * Row #3- log scale of #2; PSF iso-contours shown in solid line, elliptical Gaussian fit iso-contours shown in broken line | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | <gallery widths=500px heights=500px perrow=1 caption="Comparison images of compact sources and effective beams, PSFs"> | ||
| + | File:30.png| '''30GHz''' | ||
| + | </gallery> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Histograms of the effective beam parameters=== | ||
| + | |||
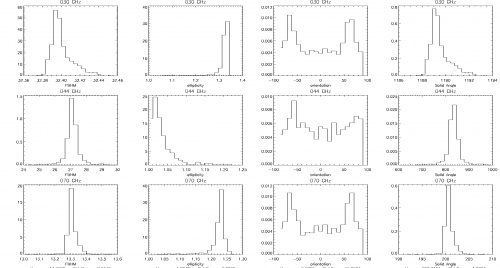
| + | Here we present histograms of the three fit parameters - beam FWHM, ellipticity, and orientation with respect to the local meridian and of the beam solid angle. The shy is sampled (pretty sparsely) at 3072 directions which were chosen as HEALpix nside=16 pixel centers for HFI and at 768 directions which were chosen as HEALpix nside=8 pixel centers for LFI to uniformly sample the sky. | ||
| + | |||
| + | Where beam solid angle is estimated according to the definition: '''4pi* sum(effbeam)/max(effbeam)''' | ||
| + | ie <math> 4 \pi \sum(B_{ij}) / max(B_{ij}) </math> | ||
| + | |||
| + | |||
| + | [[File:ist_GB.png | 500px| thumb | center| '''Histograms for LFI effective beam parameters''' ]] | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Sky variation of effective beams solid angle and ellipticity of the best-fit Gaussian=== | ||
| + | |||
| + | |||
| + | |||
| + | <gallery widths=400px heights=400px perrow=2 caption="Sky variation of effective beams solid angle and ellipticity of the best-fit Gaussian"> | ||
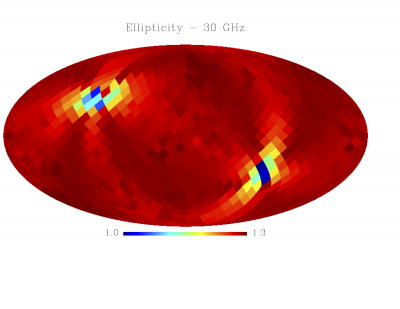
| + | File:e_030_GB.png| '''ellipticity - 30GHz''' | ||
| + | File:solidarc_030_GB.png| '''beam solid angle (relative variations wrt scanning beam - 30GHz''' | ||
| + | </gallery> | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ===Statistics of the effective beams computed using FEBeCoP=== | ||
| + | |||
| + | We tabulate the simple statistics of FWHM, ellipticity (e), orientation (<math> \psi</math>) and beam solid angle, (<math> \Omega </math>), for a sample of 3072 and 768 directions on the sky for HFI and LFI data respectively. Statistics shown in the Table are derived from the histograms shown above. | ||
| + | |||
| + | * The derived beam parameters are representative of the DPC NSIDE 1024 and 2048 healpix maps (they include the pixel window function). | ||
| + | * The reported FWHM_eff are derived from the beam solid angles, under a Gaussian approximation. These are best used for flux determination while the the Gaussian fits to the effective beam maps are more suited for source identification. | ||
| + | |||
| + | |||
| + | |||
| + | {| border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
| + | |+ '''Statistics of the FEBeCoP Effective Beams Computed with the BS Mars12 apodized for the CMB channels and oversampled''' | ||
| + | |- | ||
| + | ! '''frequency''' || '''mean(fwhm)''' [arcmin] || '''sd(fwhm)''' [arcmin] || '''mean(e)''' || '''sd(e)''' || '''mean(<math> \psi</math>)''' [degree] || '''sd(<math> \psi</math>)''' [degree] || '''mean(<math> \Omega </math>)''' [arcmin<math>^{2}</math>] || '''sd(<math> \Omega </math>)''' [arcmin<math>^{2}</math>] || '''FWHM_eff''' [arcmin] | ||
| + | |- | ||
| + | | 030 || 32.239 || 0.013 || 1.320 || 0.031 || -0.304 || 55.349 || 1189.513 || 0.842 || 32.34 | ||
| + | |- | ||
| + | | 044 || 27.005 || 0.552 || 1.034 || 0.033 || 0.059 || 53.767 || 832.946 || 31.774 || 27.12 | ||
| + | |- | ||
| + | | 070 || 13.252 || 0.033 || 1.223 || 0.026 || 0.587 || 55.066 || 200.742 || 1.027 || 13.31 | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ====Beam solid angles for the PCCS==== | ||
| + | |||
| + | ** <math>\Omega_{eff}</math> - is the mean beam solid angle of the effective beam, where beam solid angle is estimated according to the definition: 4pi*sum(effbeam)/max(effbeam), i.e. as an integral over the full extent of the effective beam, i.e. <math> 4 \pi \sum(B_{ij}) / max(B_{ij}) </math>. | ||
| + | |||
| + | ** from <math>\Omega_{eff}</math> we estimate the <math>fwhm_{eff}</math>, under a Gaussian approximation - these are tabulated above | ||
| + | ** <math>\Omega^{(1)}_{eff}</math> is the beam solid angle estimated up to a radius equal to one <math>fwhm_{eff}</math> and <math>\Omega^{(2)}_{eff}</math> up to a radius equal to twice the <math>fwhm_{eff}</math>. | ||
| + | *** These were estimated according to the procedure followed in the aperture photometry code for the PCCS: if the pixel centre does not lie within the given radius it is not included (so inclusive=0 in query disc). | ||
| + | |||
| + | |||
| + | {|border="1" cellpadding="5" cellspacing="0" align="center" style="text-align:center" | ||
| + | |+'''Band averaged beam solid angles''' | ||
| + | | '''Band''' || '''<math>\Omega_{eff}</math>'''[arcmin<math>^{2}</math>] || '''spatial variation''' [arcmin<math>^{2}</math>] || '''<math>\Omega^{(1)}_{eff}</math>''' [arcmin<math>^{2}</math>]|| '''spatial variation-1''' [arcmin<math>^{2}</math>] || '''<math>\Omega^{(2)}_{eff}</math>''' [arcmin<math>^{2}</math>] || '''spatial variation-2''' [arcmin<math>^{2}</math>] | ||
| + | |- | ||
| + | |30 || 1189.513 || 0.842 || 1116.494 || 2.274 || 1188.945 || 0.847 | ||
| + | |- | ||
| + | | 44 || 832.946 || 31.774 || 758.684 || 29.701 || 832.168 || 31.811 | ||
| + | |- | ||
| + | | 70 || 200.742 || 1.027 || 186.260 || 2.300 || 200.591 || 1.027 | ||
| + | |} | ||
| + | |||
| + | |||
== Window Functions == | == Window Functions == | ||
Revision as of 00:46, 13 March 2013
Contents
- 1 Overview
- 2 Main Beams and Focal Plane calibration
- 3 Effective beams
- 4 Window Functions
- 5 Sidelobes
- 6 References
Overview[edit]
LFI is observing the sky with 11 pairs of beams associated with the 22 pseudo-correlation radiometers. Each beam of the radiometer pair (Radiometer Chain Assembly - RCA) is named as LFIXXM or LFIXXS. XX is the RCA number ranging from 18 to 28; M and S are the two polarization namely main-arm and side-arm of the Orthomode transducers #darcangelo2009b (see also LFI naming convention).
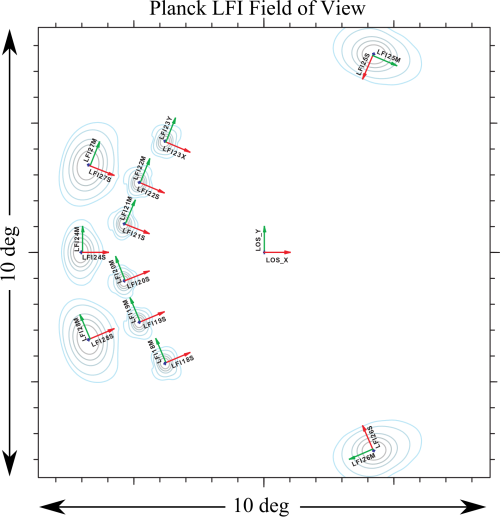
Main Beams and Focal Plane calibration[edit]
As the focal plane calibration we refer to the determination of the beam pointing parameters in the nominal Line of Sight (LOS) frame through main beam measurments using Jupiter transits. the parametes that characterise the beam pointing are the following:
- THETA_UV ($\theta_{uv}$)
- PHI_UV ($\phi_{uv}$)
They are calculated starting from u,v coordinates derived form the beam reconstruction algorithm as
$\theta_{uv} = \arcsin(u^2+v^2)$
$\phi_{uv} = \arctan(v/u)$
Two additional angles are used to characterize the beams in the RIMO:
- PSI_UV ($\psi_{uv}$)
- PSI_POL ($\psi_{pol}$)
$\psi_{uv}$ and $\psi_{pol}$ are not derived from measurements but they are extimated form optical simulations. They are the quantities that represent the polarization direction of each beam, in the following approximation: the M- and S- beams of the same RCA point at the same direction on the sky.
The main beams are characterised by 2 method:
- elliptical (or bivariate) gaussian fit as in #[planck2011-1-6] with modification explained in #[planck2013-p02d]. This method is used to determine
- the beam centre
- the average full width half maximum defined as $\sqrt{FWHM_{max}\cdot FWHM_{min}}$
- the beam ellipticity defined as $FWHM_{max}\over{FWHM_{min}}$
- the beam tilting, $\psi_{ell}$, with respect the u-axis.
- Electromagnetic simulation (using GRASP Physical Optics code) by appropriately tuning the Radio Frequency Flight Model (RFFM) #tauber2010b. The Radio Frequency Tuned Model, called RFTM, was implemented to fit the beam data with electromagnetic model. It is derived as follow:
- the Focal plane unit electromagnetic model has shifted by 3.5mm toward the secondary mirror;
- All the simulated beams where monochromatic, i.e calculated at a single frequency called Optical Center Frequency (OCF). For the RFTM model the OCF has been chosen at $28.0$, $44.0$, $70.0$. In fact the optical and radiometer bandshapes as reported in #zonca2009 demonstrates that for the 30 GHz channel, the radiometer responses are better described by a central frequency closer to 28 GHz with respect to the nominal one, whereas for the other two frequency channels the OCF is close to the nominal one.
- each feed horn phase centre has been moved alogn horn axis to optimize the match between simulations and data. The optimization was obtained by minimizing the variance according to the following definition: If $B_s[u,v]$ is the peak-normalized scanning beam matrix (for semplicity we use here $(u,v)$ coordinates also as indexes of the beam matrix) and $B_o[u,v]$ is the smeared peak-normalized simulated GRASP beam, the variance, $\sigma$, can be evaluated for each beam:
\begin{eqnarray} \label{eqsigma} \sigma &=& {\sum_{u,v}{(f[u,v] - \overline{f})^2}}\cdot {1\over N} \\ f[u,v]&=&w[u,v] \cdot (B^{dB}_s(u,v)- B^{dB}_o(u,v)) \\ w[u,v]&=&\sqrt{T[u,v]} \end{eqnarray} where also $T[u,v]$ is the temperature or the scanning beam not normalized to peak, and $N$ is the number of points considered in the comparison so that the number of point in the (u,v) plane. The parameter $\sigma$, as already said, is the variance of the difference between two beams weighted by the measured beam itself. For each beam the variance has computed computed down to $-15$dB from beam peak to avoid bias due to noise and background. The comparison between the simulated RFTM beams and the data are reported in #planck2013-p02d
Effective beams[edit]
The effective beam is the average of all scanning beams pointing at a certain direction within a given pixel of the sky map for a given scan strategy. It takes into account the coupling between azimuthal asymmetry of the beam and the uneven distribution of scanning angles across the sky. It captures the complete information about the difference between the true and observed image of the sky. They are, by definition, the objects whose convolution with the true CMB sky produce the observed sky map.
The full algebra involving the effective beams for temperature and polarisation was presented in [Mitra, Rocha, Gorski et al.] #mitra2010. Here we summarise the main results. The observed temperature sky is a convolution of the true sky and the effective beam :
where
is time samples, is if the pointing direction falls in pixel number , else it is , represents the exact pointing direction (not approximated by the pixel centre location), and is the centre of the pixel number , where the scanbeam is being evaluated (if the pointing direction falls within the cut-off radius of FWHM.
The algebra is a bit more involved for polarised detectors. The observed stokes parameters at a pixel , , are related to the true stokes parameters , by the following relation:
where the polarised effective beam matrix
and and are the the polarisation weight vectors, as defined in \cite{mitra2010}.
The task is to compute for temperature only beams and the matrices for each pixel , at every neighbouring pixel that fall within the cut-off radius around the the center of the pixel.
The effective beam is computed by stacking within a small field around each pixel of the HEALPix sky map. Due to the particular features of Planck scanning strategy coupled to the beam asymmetries in the focal plane, and data processing of the bolometer and radiometer TOIs, the resulting Planck effective beams vary over the sky.
FEBeCoP, given information on Planck scanning beams and detector pointing during a mission period of interest, provides the pixelized stamps of both the Effective Beam, EB, and the Point Spread Function, PSF, at all positions of the HEALPix-formatted map pixel centres.
Comparison of the images of compact sources observed by Planck with FEBeCoP products[edit]
We show here a comparison of the FEBeCoP derived effective beams, and associated point spread functions,PSF (the transpose of the beam matrix), to the actual images of a few compact sources observed by Planck, for 30GHz and 100GHz frequency channels, as an example. We show below a few panels of source images organized as follows:
- Row #1- DX9 images of four ERCSC objects with their galactic (l,b) coordinates shown under the color bar
- Row #2- linear scale FEBeCoP PSFs computed using input scanning beams, Grasp Beams, GB, for LFI and B-Spline beams,BS, Mars12 apodized for the CMB channels and the BS Mars12 for the sub-mm channels, for HFI (see section Inputs below).
- Row #3- log scale of #2; PSF iso-contours shown in solid line, elliptical Gaussian fit iso-contours shown in broken line
- Comparison images of compact sources and effective beams, PSFs
Histograms of the effective beam parameters[edit]
Here we present histograms of the three fit parameters - beam FWHM, ellipticity, and orientation with respect to the local meridian and of the beam solid angle. The shy is sampled (pretty sparsely) at 3072 directions which were chosen as HEALpix nside=16 pixel centers for HFI and at 768 directions which were chosen as HEALpix nside=8 pixel centers for LFI to uniformly sample the sky.
Where beam solid angle is estimated according to the definition: 4pi* sum(effbeam)/max(effbeam) ie
Sky variation of effective beams solid angle and ellipticity of the best-fit Gaussian[edit]
- Sky variation of effective beams solid angle and ellipticity of the best-fit Gaussian
Statistics of the effective beams computed using FEBeCoP[edit]
We tabulate the simple statistics of FWHM, ellipticity (e), orientation () and beam solid angle, (), for a sample of 3072 and 768 directions on the sky for HFI and LFI data respectively. Statistics shown in the Table are derived from the histograms shown above.
- The derived beam parameters are representative of the DPC NSIDE 1024 and 2048 healpix maps (they include the pixel window function).
- The reported FWHM_eff are derived from the beam solid angles, under a Gaussian approximation. These are best used for flux determination while the the Gaussian fits to the effective beam maps are more suited for source identification.
| frequency | mean(fwhm) [arcmin] | sd(fwhm) [arcmin] | mean(e) | sd(e) | mean() [degree] | sd() [degree] | mean() [arcmin] | sd() [arcmin] | FWHM_eff [arcmin] |
|---|---|---|---|---|---|---|---|---|---|
| 030 | 32.239 | 0.013 | 1.320 | 0.031 | -0.304 | 55.349 | 1189.513 | 0.842 | 32.34 |
| 044 | 27.005 | 0.552 | 1.034 | 0.033 | 0.059 | 53.767 | 832.946 | 31.774 | 27.12 |
| 070 | 13.252 | 0.033 | 1.223 | 0.026 | 0.587 | 55.066 | 200.742 | 1.027 | 13.31 |
Beam solid angles for the PCCS[edit]
- - is the mean beam solid angle of the effective beam, where beam solid angle is estimated according to the definition: 4pi*sum(effbeam)/max(effbeam), i.e. as an integral over the full extent of the effective beam, i.e. .
- from we estimate the , under a Gaussian approximation - these are tabulated above
- is the beam solid angle estimated up to a radius equal to one and up to a radius equal to twice the .
- These were estimated according to the procedure followed in the aperture photometry code for the PCCS: if the pixel centre does not lie within the given radius it is not included (so inclusive=0 in query disc).
| Band | [arcmin] | spatial variation [arcmin] | [arcmin] | spatial variation-1 [arcmin] | [arcmin] | spatial variation-2 [arcmin] |
| 30 | 1189.513 | 0.842 | 1116.494 | 2.274 | 1188.945 | 0.847 |
| 44 | 832.946 | 31.774 | 758.684 | 29.701 | 832.168 | 31.811 |
| 70 | 200.742 | 1.027 | 186.260 | 2.300 | 200.591 | 1.027 |
Window Functions[edit]
TBW
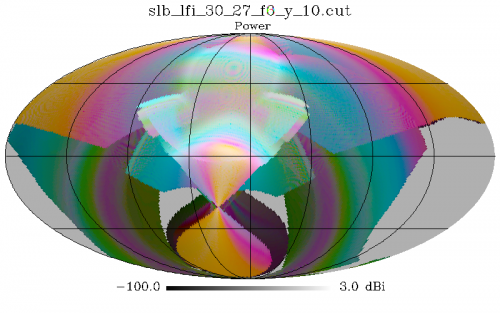
Sidelobes[edit]
There is no direct measurements of sidelobes for LFI. The sidelobe pattern for LFI was been simulated using GRASP9 Multi-reflector GTD. We used the RFTM electromagnetic model. Seven beams for each radiometer have been computed in spherical polar cuts with a step of 0.5 degrees both in theta and phi. The beams have been computed in the same frames used for the main beams. The intermediate beam region (theta < 5 degrees) has been replaced with null values.
- In the computation we considered:
- the direct field from the feed
- the 1st order contributions: Bd, Br, Pd, Pr, Sd, Sr, Fr
- the 2nd order contributions SrPd and SdPd
where B=buffle', P=primary reflector, S=secondary reflector, F=Focal Plane Unit Box. and where d=diffraction, r=reflection. For example Br, means that we considered in the calculation the reflection on the telescope baffle system.
A refinement of the sidelobes model will be considered in a future release, taking into account more contributions together with Physical Optics models.
References[edit]
<biblio force=false>
</biblio>
(Planck) Low Frequency Instrument
LFI Radiometer Chain Assembly
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
Line Of Sight
reduced IMO
Full-Width-at-Half-Maximum
Cosmic Microwave background
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
Early Release Compact Source Catalog
(Planck) High Frequency Instrument
Data Processing Center