Difference between revisions of "Astrophysical component separation"
| Line 99: | Line 99: | ||
: All nine Planck frequency channels from 30 to 857 GHz, harmonically transformed up to <math>\ell = 4000 </math>. | : All nine Planck frequency channels from 30 to 857 GHz, harmonically transformed up to <math>\ell = 4000 </math>. | ||
; Fit | ; Fit | ||
| − | : In practice, the SMICA fit,i.e.,the minimization of | + | : In practice, the SMICA fit,i.e.,the minimization of Eq. (4), is conducted in three successive steps: We first estimate the CMB spectral law by fitting all model parameters over a clean fraction of sky in the range <math> 100 ≤ \ell ≤ 680</math> and retaining the best fit value for vector <math> \mathbf{a}</math>. In the second step, we estimate the foreground emissivity by fixing a to its value from the previous step and fitting all the other parameters over a large fraction of sky in the range <math> 4 ≤ \ell ≤ 150</math> and retaining the best fit values for the matrix <math> \mathbf{A}</math>. In the last step, we fit all power spectrum parameters; that is, we fix <math>\mathbf{a}</math> and <math>\mathbf{A}</math> to their previously found values and fit for each <math> C_\ell </math> and <math>\mathbf{P}_\ell </math> at each <math>\ell</math>. |
;Beams | ;Beams | ||
: The discussion thus far assumes that all input maps have the same resolution and effective beam. Since the observed maps actually vary in resolution, we process the input maps in the following way. To the <math>i</math>-th input map with effective beam <math>b_i(\ell)</math> and sampled on an HEALPix grid with <math>N^i_{side}</math>, the CMB sky multipole <math>s_{\ell m}</math> actually contributes <math>s_{\ell m}a_i b_i(\ell) p_i(\ell)</math>, where <math>p_i(\ell)</math> is the pixel window function for the grid at <math>N^i_{side}</math>. Seeking a final CMB map at 5-arcmin resolution, the highest resolution of Planck, we work with input spherical harmonics re-beamed to 5 arcmins, <math>\mathbf{\tilde{x}}_{\ell m} </math>; that is, SMICA operates on vectors with entries <math>x ̃^i_{\ell m} = x^i_{\ell m} b_5(\ell) / b_i(\ell) / p_i(\ell)</math>, where <math>b_5(\ell)</math> is a 5 arcmin Gaussian beam function. By construction, SMICA then produces an CMB map with an effective Gaussian beam of 5 arcmin (without the pixel window function). | : The discussion thus far assumes that all input maps have the same resolution and effective beam. Since the observed maps actually vary in resolution, we process the input maps in the following way. To the <math>i</math>-th input map with effective beam <math>b_i(\ell)</math> and sampled on an HEALPix grid with <math>N^i_{side}</math>, the CMB sky multipole <math>s_{\ell m}</math> actually contributes <math>s_{\ell m}a_i b_i(\ell) p_i(\ell)</math>, where <math>p_i(\ell)</math> is the pixel window function for the grid at <math>N^i_{side}</math>. Seeking a final CMB map at 5-arcmin resolution, the highest resolution of Planck, we work with input spherical harmonics re-beamed to 5 arcmins, <math>\mathbf{\tilde{x}}_{\ell m} </math>; that is, SMICA operates on vectors with entries <math>x ̃^i_{\ell m} = x^i_{\ell m} b_5(\ell) / b_i(\ell) / p_i(\ell)</math>, where <math>b_5(\ell)</math> is a 5 arcmin Gaussian beam function. By construction, SMICA then produces an CMB map with an effective Gaussian beam of 5 arcmin (without the pixel window function). | ||
| Line 111: | Line 111: | ||
: Since there is little point trying to model the spectral covariance at high multipoles, because the sample estimate is sufficient, SMICA implements a simple harmonic ILC at <math>l > 1500</math>; that is, it applies the filter (Eq. 2) with <math>\mathbf{R}_\ell = \mathbf{\hat{R}}_\ell</math>. | : Since there is little point trying to model the spectral covariance at high multipoles, because the sample estimate is sufficient, SMICA implements a simple harmonic ILC at <math>l > 1500</math>; that is, it applies the filter (Eq. 2) with <math>\mathbf{R}_\ell = \mathbf{\hat{R}}_\ell</math>. | ||
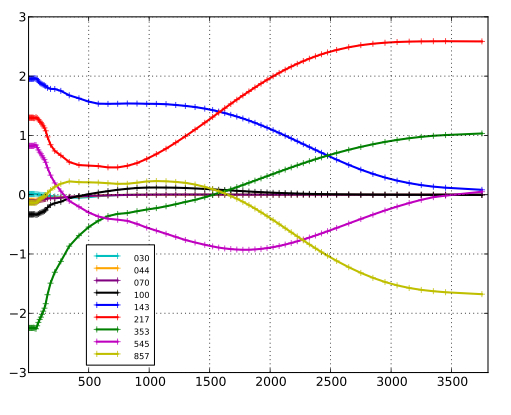
| − | Viewed as a filter, SMICA can be summarized by the weights <math>\mathbf{w}_\ell</math> applied to each input map as a function of multipole. In this sense, SMICA is strictly equivalent to co-adding the input maps after convolution by specific axi-symmetric kernels directly related to the corresponding entry of <math>\mathbf{w}_\ell</math>. The SMICA weights used here are shown in | + | Viewed as a filter, SMICA can be summarized by the weights <math>\mathbf{w}_\ell</math> applied to each input map as a function of multipole. In this sense, SMICA is strictly equivalent to co-adding the input maps after convolution by specific axi-symmetric kernels directly related to the corresponding entry of <math>\mathbf{w}_\ell</math>. The SMICA weights used here are shown in figure below for input maps in units of K<math>_\rm{RJ}</math>. They show, in particular, the (expected) progressive attenuation of the lowest resolution channels with increasing multipole. |
| − | [[File:smica.jpg|thumb|center|600px|''' | + | [[File:smica.jpg|thumb|center|600px|'''Weights <math>w_\ell</math> given by SMICA to the input maps, after they are re-beamed to 5 arcmin and expressed in K<math>_\rm{RJ}</math>), as a function of multipole.''']] |
===Commander-Ruler=== | ===Commander-Ruler=== | ||
Revision as of 16:37, 17 March 2013
CMB and foreground separation[edit]
NILC[edit]
NILC is a linear method for combining the input channels.
It implements an ILC with weighting coefficients varying over the sky and over the multipole range up to l=3200.
It does so using 'needlets' which are spherical wavelets.
A special procedure is used for processing the coarsest needlet scale which contains the large scale multipoles.
See the Component Separation paper for details.
SEVEM[edit]
The aim of Sevem is to produce clean CMB maps at one or several frequencies by using a procedure based on template fitting. The templates are internal, i.e., they are constructed from Planck data, avoiding the need for external data sets, which usually complicates the analyses and may introduce inconsistencies. The method has been successfully applied to Planck simulations Leach et al., 2008 and to WMAP polarisation data Fernandez-Cobos et al., 2012. In the cleaning process, no assumptions about the foregrounds or noise levels are needed, rendering the technique very robust.
The input maps used are all the Planck frequency channels. In particular, we have cleaned the 100, 143 GHz and 217 GHz maps using four templates constructed as the difference of the following Planck channels (smoothed to a common resolution): (30-44) GHz, (44-70) GHz, (545-353) GHz and (857-545)GHz.
The templates are constructed by subtracting two neighbouring Planck frequency channel maps, after first smoothing them to a common resolution to ensure that the CMB signal is properly removed. A linear combination of the templates is then subtracted from the Planck sky map at the frequency to be cleaned, in order to produce the clean CMB. The coefficients of the linear combination are obtained by minimising the variance of the clean map outside a given mask. Although we exclude very contaminated regions during the minimization, the subtraction is performed for all pixels and, therefore, the cleaned maps cover the full-sky (although we expect that foreground residuals are present in the excluded areas).
An additional level of flexibility can also be considered: the linear coefficients can be the same for all the sky, or several regions with different sets of coefficients can be considered. The regions are then combined in a smooth way, by weighting the pixels at the boundaries, to avoid discontinuities in the clean maps. In order to take into account the different spectral behaviour of the foregrounds at low and high galactic latitudes, we have chosen to use two regions: the region with the 3 per cent brightest Galactic emission, and the region with the remaining 97 per cent of the sky.
The final CMB map has then been constructed by combining the 143 and 217 GHz cleaned maps by weighting the maps in harmonic space taking into account the noise level, the resolution and a rough estimation of the foreground residuals of each map (obtained from realistic simulations). This final map has a resolution corresponding to a Gaussian beam of FWHM =5 arcminutes.
SMICA[edit]
A linear method, SMICA reconstructs a CMB map as a linear combination in the harmonic domain of input frequency maps with weights that depend on multipole . Given the vector of spherical harmonic coefficients for the input maps, it computes coefficients for the CMB map as
where the vector which contains the multipole-dependent weights is built to offer unit gain to the CMB with minimum variance. This is achieved with
where vector is the emission spectrum of the CMB evaluated at each channel (allowing for possible inter-channel recalibration factors) and is the spectral covariance matrix of . Taking in Eq. \ref{eq:smica:w} to be the sample spectral covariance matrix of the observations:
would implement a simple harmonic-domain ILC. This is not what SMICA does. As discussed below, we instead use a model and determine the covariance matrix to be used in Eq. \ref{eq:smica:w} by fitting to . This is done in the maximum likelihood sense for stationary Gaussian fields, yielding the best fit model parameters θ as
SMICA models the data is a superposition of CMB, noise and
foregrounds. The latter are not parametrically modelled; instead, we
represent the total foreground emission by templates
with arbitrary frequency spectra, angular spectra and correlations:
where is the angular power spectrum of the CMB, is a matrix, is a positive matrix, and is a diagonal matrix representing the noise power spectrum. The parameter vector contains all or part of the quantities in Eq. (5).
The above equations summarize the founding principles of SMICA; its
actual operation depends on a choice for the spectral model
and on several
implementation-specific details.
The actual implementation of SMICA includes the following steps:
- Inputs
- All nine Planck frequency channels from 30 to 857 GHz, harmonically transformed up to .
- Fit
- In practice, the SMICA fit,i.e.,the minimization of Eq. (4), is conducted in three successive steps: We first estimate the CMB spectral law by fitting all model parameters over a clean fraction of sky in the range and retaining the best fit value for vector . In the second step, we estimate the foreground emissivity by fixing a to its value from the previous step and fitting all the other parameters over a large fraction of sky in the range and retaining the best fit values for the matrix . In the last step, we fit all power spectrum parameters; that is, we fix and to their previously found values and fit for each and at each .
- Beams
- The discussion thus far assumes that all input maps have the same resolution and effective beam. Since the observed maps actually vary in resolution, we process the input maps in the following way. To the -th input map with effective beam and sampled on an HEALPix grid with , the CMB sky multipole actually contributes , where is the pixel window function for the grid at . Seeking a final CMB map at 5-arcmin resolution, the highest resolution of Planck, we work with input spherical harmonics re-beamed to 5 arcmins, ; that is, SMICA operates on vectors with entries , where is a 5 arcmin Gaussian beam function. By construction, SMICA then produces an CMB map with an effective Gaussian beam of 5 arcmin (without the pixel window function).
- Pre-processing
- We start by fitting point sources with SNR > 5 in the PCCS catalogue in each input map. If the fit is successful, the fitted point source is removed from the map; otherwise it is masked and the hole in-painted. This is done at all frequencies but 545 and 857 GHz, where all point sources with SNR > 7.5 are masked and in-painted.
- Masking and in-painting
- In practice, SMICA uses a small Galactic mask leaving 97% of the sky. We deliver a full-sky CMB map in which the masked pixels (Galactic and point-source) are replaced by a constrained Gaussian realization.
- Binning
- In our implementation, we use binned spectra.
- High
- Since there is little point trying to model the spectral covariance at high multipoles, because the sample estimate is sufficient, SMICA implements a simple harmonic ILC at ; that is, it applies the filter (Eq. 2) with .
Viewed as a filter, SMICA can be summarized by the weights applied to each input map as a function of multipole. In this sense, SMICA is strictly equivalent to co-adding the input maps after convolution by specific axi-symmetric kernels directly related to the corresponding entry of . The SMICA weights used here are shown in figure below for input maps in units of K. They show, in particular, the (expected) progressive attenuation of the lowest resolution channels with increasing multipole.
Commander-Ruler[edit]
Cosmic Microwave background
Full-Width-at-Half-Maximum
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).