HFI design, qualification, and performance
The inversion of HFI data requires that one knows how the instrument selects photons, how these photons are transformed in data transmitted by telemetry and what spurious signals are added in this process.
Contents
[hide]HFI high level description and Architecture[edit]
(Lamarre/Pajot) Should be short, understandable and point through links to the relevant sections and papers.
Cryogenics[edit]
(F .Pajot)
Dilution[edit]
(including PIDs)
The HFI 3He-4He dilution cooler produces temperatures of 0.1 K for the bolometers through the dilution of 3He into 4He and 1.4 K through JT expansion of the 3He and 4He mixture. The dilution cooler is described in detail in [Planck early results. II. The thermal performance of Planck, 2.3.3. Dilution cooler].
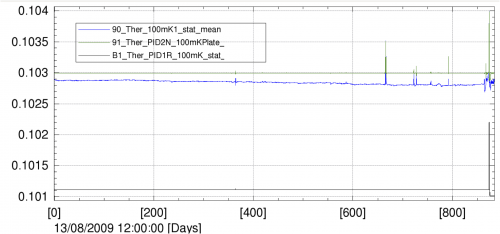
The dilution was operated with flows set to the minimum available value, and provided a total lifetime of 30.5 months, exceeding the nominal lifetime of 16 months by 14.5 months. The dilution stage was stabilized by a PID control with a power comprised between 20 and 30 nW providing a temperature near 101 mK. The bolometer plate was stabilized at 102.8 mK with a PID power around 5 nW [fig. 100mK_stability.png].
(here a few lines of 100 mK boloplate stability)
Detailed of the in-flight performance of the dilution cooler can be found in [Planck early results. II. The thermal performance of Planck, 4.4. Dilution cooler]
4K J-T cooler[edit]
(including PIDs for details links to the early cryogenic paper (need to add data ?))
The HFI 4K J-T cooler produces a temperature of 4K for the HFI 4K stage and optics and the precooling of the dilution gases. Full description of the 4K cooler can be found in [Planck early results. II. The thermal performance of Planck, 2.3.2. 4He-JT cooler].
The 4K cooler was operated without interruption during all the survey phase of the mission. It is still in operation as it also provides the cooling of the optical reference loads of the LFI. The 4K PID stabilizing the temperature of the HFI optics is regulated at 4.81 K using a power around 1.8 mW [fig. 4K -A VENIR-].
(here a few lines of 4K stability, including compressors operation)
Details on the in-flight performance of the dilution cooler can be found in [Planck early results. II. The thermal performance of Planck, 4.3. 4He-JT cooler]
Cold optics[edit]
(Lamarre)
Horns,lenses[edit]
links to Peter's paper
filters, band[edit]
Includes Locke's very detailed document.
Detection chain[edit]
(Francesco Piacentini)
Bolometers[edit]
JFETs[edit]
Readout[edit]
Data compression[edit]
Time response.[edit]
Links to Brendan's paper. Additional data if needed. Written by Brendan.
The time response of the HFI bolometers and readout electronics is modelled as a Fourier domain transfer function (called the LFER4 model) consisting of the product of an bolometer thermal response and an electronics response .
In the processing of the HFI data, the time response is deconvolved (see TOI processing section).
LFER4 model[edit]
If we write the input signal (power) on a bolometer as the bolometer physical impedance can be written as: where is the angular frequency of the signal and is the complex intrinsic bolometer transfer function. For HFI the bolometer transfer function is modelled as the sum of 4 single pole low pass filters: The modulation of the signal is done with a square wave, written here as a composition of sine waves of decreasing amplitude: where we have used the Euler relation and is the angular frequency of the square wave. The modulation frequency is and was set to Hz in flight. This signal is then filtered by the complex electronic transfer function . Setting: we have: This signal is then sampled at high frequency (). is one of the parameters of the HFI electronics and corresponds to the number of high frequency samples in each modulation semi-period. In order to obtain an output signal sampled every seconds, we must integrate on a semiperiod, as done in the HFI readout. To also include a time shift , the integral is calculated between and (with period of the modulation). The time shift is encoded in the HFI electronics by the parameter , with the relation .
After integration, the -sample of a bolometer can be written as where
The output signal in equation eqn:output can be demodulated (thus removing the ) and compared to the input signal in equation bol_in. The overall transfer function is composed of the bolometer transfer function and the effective electronics transfer function, :
The shape of is obtained combining low and high-pass filters with Sallen Key topologies (with their respective time constants) and accounting also for the stray capacitance low pass filter given by the bolometer impedance combined with the stray capacitance of the cables. The sequence of filters that define the electronic band-pass function are listed in table table:readout_electronics_filters.
Parameters of LFER4 model[edit]
The LFER4 model has are a total of 10 parameters, 9 of which are independent, for each bolometer. The free parameters of the LFER4 model are determined using in-flight data in the following ways:
{itemize} is fixed at the value of the REU setting.
is measured during the QEC test during CPV.
, , , are fit forcing the compactness of the scanning beam.
, , are fit by forcing agreement of survey 2 and survey 1 maps.
the overall normalization of the LFER4 model is forced to be 1.0 at the signal frequency of the dipole.
The details of determining the model parameters are given in (reference P03c paper) and the best-fit parameters listed here in table table:LFER4pars.
HFI electronics filter sequence. We define $s = i \omega$.
{HFI electronics filter sequence. We define $s = i \omega$.}(table:readout_electronics_filters)
&Filter& Parameters&Function{\vskip 3pt\hrule\vskip 5pt}0&Stray capacitance low pass filter& & 1&Low pass filter& k
nF & 2&Sallen Key high pass filter &k
F&3&Sign reverse with gain &&4&Single pole low pass filter with gain &k
nF&5&Single pole high pass filter coupled to a Sallen Key low pass filter&k
k
nF
k
F
&
(table:readout_electronics_filters)
-3mm ={
\newdimen\digitwidth
\setbox0=\hbox{\rm 0}
\digitwidth=\wd0
\catcode`*=\active
\def*{\kern\digitwidth}
%
\newdimen\signwidth
\setbox0=\hbox{+}
\signwidth=\wd0
\catcode`!=\active
\def!{\kern\signwidth}
% \halign{#\tabskip 2em&
\vtop{\hsize 1.5in\noindent\strut#\strut\par}\tabskip 2em &
\vtop{\hsize 2.0in\noindent\strut#\strut\par}\tabskip 2em&
\vtop{\hsize 1.5in\noindent\strut#\strut\par}\cr % Template goes here.
\noalign{\doubleline}
% Table headings go here.
&Filter& Parameters&Function\cr \noalign{\vskip 3pt\hrule\vskip 5pt}
% Body of table goes here
0&Stray capacitance low pass filter& $\tau_{stray}= R_{bolo} C_{stray}$ & $h_0 = \frac{1}{1.0+\tau_{stray}*s}$\cr 1&Low pass filter& $R_1=1$k$\Omega$ \\ $C_1=100$nF & $h_1 = \frac{2.0+R_1*C_1*s}{2.0*(1.0+R_1*C_1*s)}$\cr 2&Sallen Key high pass filter &$R_2=51$k$\Omega$\\ $C_2=1\mu$F&$h_2= \frac{(R_2*C_2*s)^2}{(1.0+R_2*C_2*s)^2}$\cr 3&Sign reverse with gain &&$h_3=-5.1$\cr 4&Single pole low pass filter with gain &$R_4=10$k$\Omega$\\ $C_4=10$nF&$h_4= \frac{1.5}{1.0+R_4*C_4*s}$\cr 5&Single pole high pass filter coupled to a Sallen Key low pass filter&$R_9=18.7$k$\Omega$\\ $R_{12}=37.4$k$\Omega$\\ $C=10.0$nF\\ $R_{78}=510$k$\Omega$\\ $C_{18}=1.0\mu$F\\ $K_3 = R_9^2*R_{78}*R_{12}^2*C^2*C_{18}$\\ $K_2 = R_9*R_{12}^2*R_{78}*C^2+R_{9}^2*R_{12}^2*C^2+R_9*R_{12}^2*R_{78}*C_{18}*C$\\ $K_1 =R_9*R_{12}^2*C+R_{12}*R_{78}*R_9*C_{18}$&$h_{5} = \frac{2.0*R_{12}*R_9*R_{78}*C_{18}*s}{s^3*K_3 +
s^2*K_2+
s*K_1 + R_{12}*R_9 } $\cr
\noalign{\vskip 5pt\hrule\vskip 3pt}}}
=5pt {Parameters for LFER4 model that are deconvolved from the data.}
(table:LFER4pars)
-3mm ={ \newdimen\digitwidth \setbox0=\hbox{\rm 0} \digitwidth=\wd0 \catcode`*=\active \def*{\kern\digitwidth} % \newdimen\signwidth \setbox0=\hbox{+} \signwidth=\wd0 \catcode`!=\active \def!{\kern\signwidth} % \halign{#\hfil \tabskip 2em&\hfil# \tabskip 1em&#\hfil \tabskip 1em &\hfil# \tabskip 1em&\hfil# \tabskip 1em&\hfil# \tabskip 1em&\hfil# \tabskip 1em&\hfil# \tabskip 1em&\hfil# \tabskip 1em&\hfil# \tabskip 1em&\hfil# \tabskip 1em\cr % Template goes here. \noalign{\doubleline} % Table headings go here. Bolometer&$A_1$&$\tau_1$&$A_2$&$\tau_2$&$A_3$&$\tau_3$&$A_4$&$\tau_4$&$\tau_{stray}$&$S_{phase}$\cr & & ms & & ms & & ms & &ms& ms &\cr \noalign{\vskip 3pt\hrule\vskip 5pt} % Body of table goes here. 100-1a&0.392& 10&0.534&20.9&0.0656&51.3&0.00833& 572&1.59&0.00139\cr 100-1b&0.484&10.3&0.463&19.2&0.0451&71.4&0.00808& 594&1.49&0.00139\cr 100-2a&0.474&6.84&0.421&13.6&0.0942&37.6&0.0106& 346&1.32&0.00125\cr 100-2b&0.126&5.84&0.717&15.1&0.142&35.1&0.0145& 293&1.38&0.00125\cr 100-3a&0.744&5.39&0.223&14.7&0.0262&58.6&0.00636& 907&1.42&0.00125\cr 100-3b&0.608&5.48&0.352&15.5&0.0321&63.6&0.00821& 504&1.66&0.00125\cr 100-4a&0.411& 8.2&0.514&17.8&0.0581&57.9&0.0168& 370&1.25&0.00125\cr 100-4b&0.687&11.3&0.282&24.3&0.0218& 62&0.00875& 431&1.38&0.00139\cr 143-1a&0.817&4.47&0.144&12.1&0.0293&38.7&0.0101& 472&1.42&0.00125\cr 143-1b&0.49&4.72&0.333&15.6&0.134&48.1&0.0435& 270&1.49&0.00125\cr 143-2a&0.909& 4.7&0.0763& 17&0.00634& 100&0.00871& 363&1.48&0.00125\cr 143-2b&0.912&5.24&0.0509&16.7&0.0244&26.5&0.0123& 295&1.46&0.00125\cr 143-3a&0.681&4.19&0.273&9.56&0.0345&34.8&0.0115& 317&1.45&0.00125\cr 143-3b&0.82&4.48&0.131&13.2&0.0354&35.1&0.0133& 283&1.61&0.000832\cr 143-4a&0.914&5.69&0.072&18.9&0.00602&48.2&0.00756& 225&1.59&0.00125\cr 143-4b&0.428&6.06&0.508&6.06&0.0554&22.7&0.00882& 84&1.82&0.00125\cr 143-5&0.491&6.64&0.397&6.64&0.0962&26.4&0.0156& 336&2.02&0.00139\cr 143-6&0.518&5.51&0.409&5.51&0.0614&26.6&0.0116& 314&1.53&0.00111\cr 143-7&0.414&5.43&0.562&5.43&0.0185&44.9&0.00545& 314&1.86&0.00139\cr 217-5a&0.905&6.69&0.0797&21.6&0.00585&65.8&0.00986& 342&1.57&0.00111\cr 217-5b&0.925&5.76&0.061& 18&0.00513&65.6&0.0094& 287&1.87&0.00125\cr 217-6a&0.844&6.45&0.0675&19.7&0.0737&31.6&0.0147& 297&1.54&0.00125\cr 217-6b&0.284&6.23&0.666&6.23&0.0384& 24&0.0117& 150&1.46&0.00111\cr 217-7a&0.343&5.48&0.574&5.48&0.0717& 23&0.0107& 320&1.52&0.00139\cr 217-7b&0.846&5.07&0.127&14.4&0.0131&47.9&0.0133& 311&1.51&0.00139\cr 217-8a&0.496&7.22&0.439&7.22&0.0521&32.5&0.0128& 382&1.79&0.00111\cr 217-8b&0.512&7.03&0.41&7.03&0.0639&27.2&0.0139& 232&1.73&0.00125\cr 217-1&0.0136&3.46&0.956&3.46&0.0271&23.3&0.00359&1.98e+03&1.59&0.00111\cr 217-2&0.978&3.52&0.014&26.1&0.00614& 42&0.00194& 686& 1.6&0.00125\cr 217-3&0.932&3.55&0.0336&3.55&0.0292&32.4&0.00491& 279&1.74&0.00125\cr 217-4&0.658&1.35&0.32&5.55&0.0174&26.8&0.00424& 473&1.71&0.00111\cr 353-3a&0.554&7.04&0.36&7.04&0.0699&30.5&0.0163& 344& 1.7&0.00125\cr 353-3b&0.219&2.68&0.671&6.95&0.0977&23.8&0.0119& 289&1.57&0.00111\cr 353-4a&0.768&4.73&0.198&9.93&0.0283&50.5&0.00628& 536&1.81&0.00125\cr 353-4b&0.684&4.54&0.224&10.8&0.0774& 80&0.0149& 267&1.66&0.00111\cr 353-5a&0.767&5.96&0.159&12.4&0.0628&30.3&0.0109& 357&1.56&0.00111\cr 353-5b&0.832&6.19&0.126&11.1&0.0324& 35&0.0096& 397&1.66&0.00111\cr 353-6a&0.0487&1.76&0.855& 6&0.0856&21.6&0.0105& 222&1.99&0.00125\cr 353-6b&0.829&5.61&0.127&5.61&0.0373&25.2&0.00696& 360&2.28&0.00111\cr 353-1&0.41&0.743&0.502&4.22&0.0811&17.7&0.0063& 329&1.32&0.00097\cr 353-2&0.747&3.09&0.225&7.26&0.0252&44.7&0.00267& 513&1.54&0.00097\cr 353-7&0.448& 0.9&0.537& 4.1&0.0122&27.3&0.00346& 433&1.78&0.00125\cr 353-8&0.718&2.23&0.261&6.08&0.0165& 38&0.00408& 268&1.77&0.00111\cr 545-1&0.991&2.93&0.00743& 26&0.00139&2.6e+03& & &2.16&0.00111\cr 545-2&0.985&2.77&0.0128& 24&0.00246&2.8e+03& & &1.87&0.00097\cr 545-4&0.972& 3&0.0277& 25&0.000777&2.5e+03& & &2.22&0.00111\cr 857-1&0.974&3.38&0.0229& 25&0.00349&2.2e+03& & &1.76&0.00111\cr 857-2&0.84&1.48&0.158&6.56&0.00249&3.2e+03& & & 2.2&0.00125\cr 857-3&0.36&0.0422&0.627& 2.4&0.0111& 17&0.002&1.9e+03&1.52&0.00126\cr 857-4&0.278& 0.4&0.719&3.92&0.00162& 90&0.00152& 800&1.49&0.000558\\\cr \cr \noalign{\vskip 3pt\hrule\vskip 5pt} } }
System (Ken)[edit]
List of systematics[edit]
Summary[edit]
(Lamarre) here remind worse sytematics and point to DPC Summary of sucess and limitations. JML. Link to early HFI in flight perf.
(Planck) High Frequency Instrument
(Planck) Low Frequency Instrument
Readout Electronic Unit
Calibration and Performance Verification
Data Processing Center