Systematic effect uncertainties
Contents
[hide]Overview[edit]
Known systematic effects in the Planck-LFI data can be divided into two broad categories: effects independent of the sky signal, which can be considered as additive or multiplicative spurious contributions to the measured timelines, and effects which are dependent on the sky and that cannot be considered independently from the observation strategy.
Here we report a brief summary of these effects, all the details can be found in Planck-2013-III[1].
Summary of uncertainties due to systematic effects[edit]
In this section we provide a top-level overview of the uncertainties due to systematic effects in the Planck-LFI CMB temperature maps and power spectra. Table 1 provides a list of these effects with short indications of their cause, strategies for removal and references to sections and/or papers where more information is found.
| Effect | Source | Control/Removal | Reference |
|---|---|---|---|
| Effects independent of sky signal (T and P) | |||
| White noise correlation | Phase switch imbalance | Diode weighting | Planck-2013-III[1] |
| 1/ noise | RF amplifiers | Pseudo-correlation and destriping | Planck-2013-III[1] |
| Bias fluctuations | RF amplifiers, back-end electronics& | Pseudo-correlation and destriping | DPC paper |
| Thermal fluctuations | 4 K, 20 K and 300 K thermal stages | Calibration, destriping | DPC paper |
| 1 Hz spikes | Back-end electronics | Template fitting and removal | DPC paper |
| Effects dependent on sky signal (T and P) | |||
| Main beam ellipticity | Main beams | Accounted for in window function | DPC paper |
| Near sidelobes pickup | Optical response at angles from the main beam | Masking of Galaxy and point sources | DPC paper |
| Far sidelobes pickup | Main and sub-reflector spillovers | Model sidelobes removed from timelines | DPC paper |
| Analogue-to-digital converter non linearity | Back-end analogue-to-digital converter | Template fitting and removal | DPC paper |
| Imperfect photometric calibration | Sidelobe pickup, radiometer noise temperature changes and other non-idealities | Calibration using the 4 K reference load voltage output | DPC paper |
| Pointing | Uncertainties in pointing reconstruction, thermal changes affecting focal plane geometry | Negligible impact anisotropy measurements | DPC paper |
| Effects specifically impacting polarization | |||
| Bandpass asymmetries | Differential orthomode transducer and receiver bandpass response | Spurious polarisation removal | DPC paper |
| Polarization angle uncertainty | Uncertainty in the polarization angle in-flight measurement | Negligible impact | DPC paper |
| Orthomode transducer cross-polarization | Imperfect polarization separation | Negligible impact | DPC paper |
The impact of 1/ noise has been assessed using half-ring noise maps normalised to the white noise estimate at each pixel obtained from the white noise covariance matrix, so that a perfectly white noise map would be Gaussian and isotropic with unit variance. Deviations from unity trace the contribution of residual 1/f noise in the final maps, which ranges from 0.06% at 70 GHz to 2% at 30 GHz. Pixel uncertainties due to other systematic effects have been calculated on simulated maps degraded at Nside = 128 at 30 and 44 GHz and Nside = 256 at 70 GHz in order to approximate the optical beam size. This downgrading has been applied in all cases a systematic effect has been evaluated at map level.
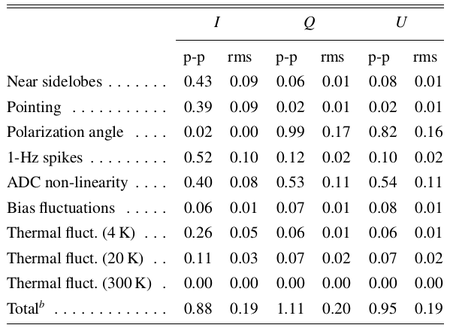
In Table 2 we list the r.m.s. and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as peak-to-peak (p-p) difference although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map.
Table 2. Summary of systematic effects uncertainties on maps in μKCMB.
|
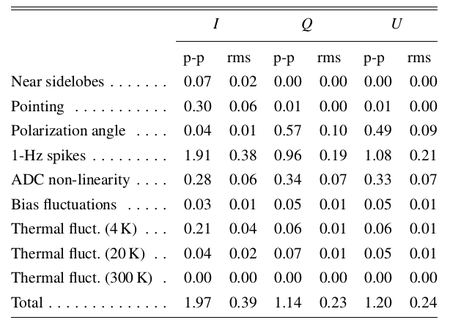
|
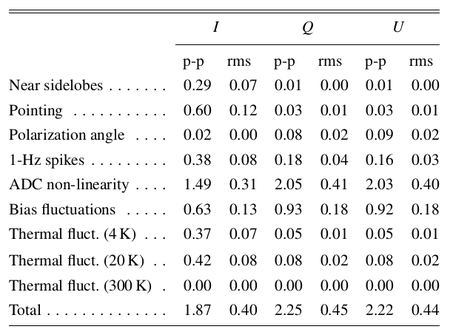
|
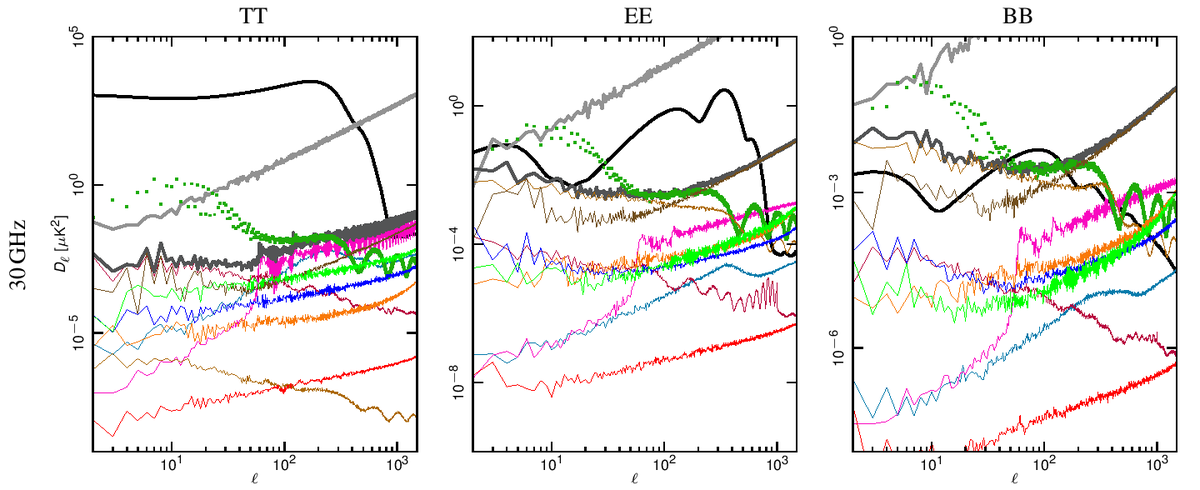
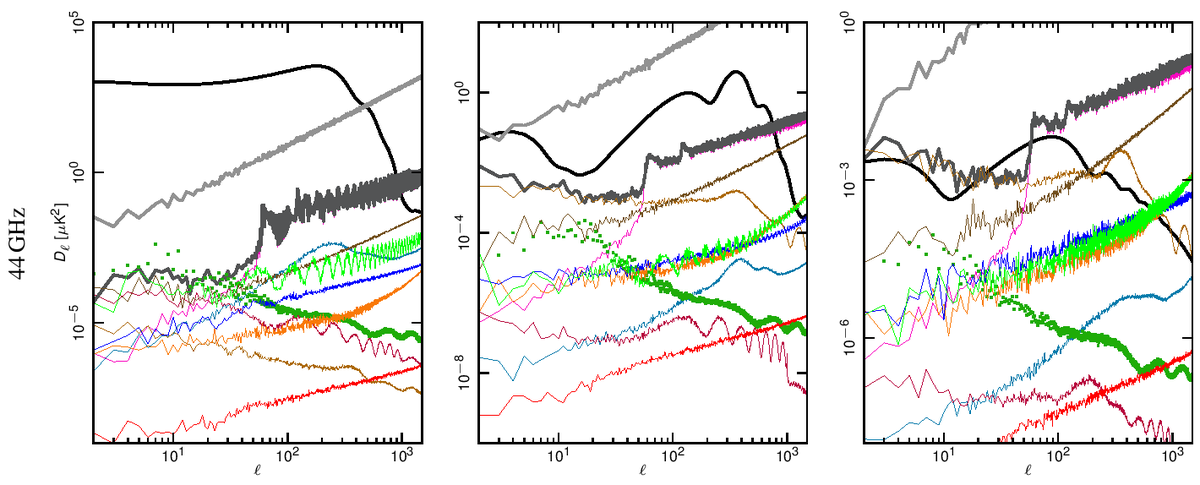
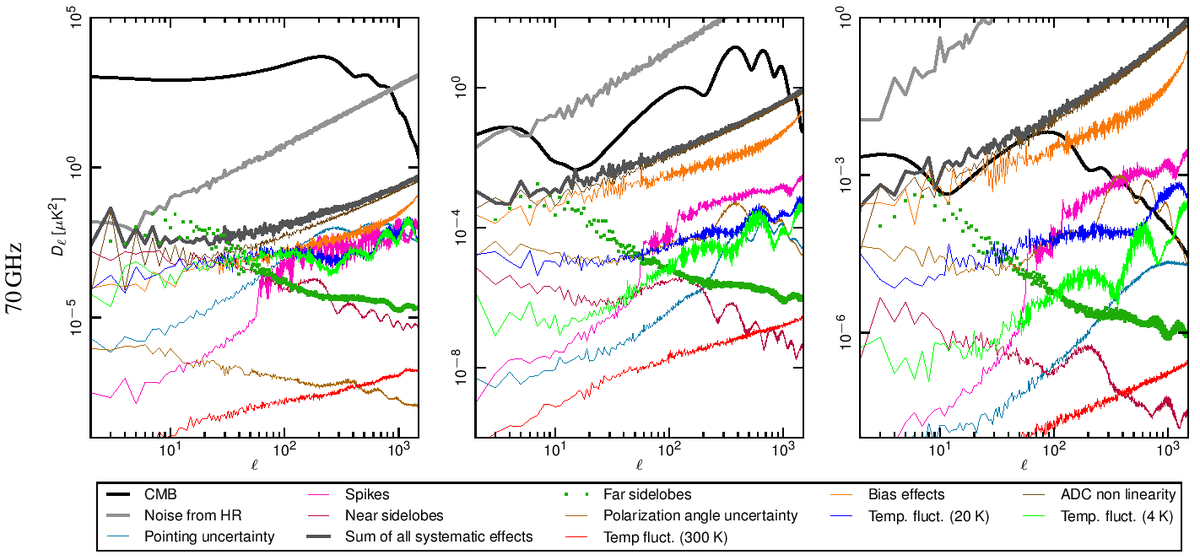
Angular power spectra have been obtained from full resolution (Nside = 1024) systematic effect maps at each frequency using HEALPix Anafast [2]. In Fig. 1 we show how the power spectrum of the various effects compared with the Planck best-fit spectra and with the noise level coming from the half-ring difference maps.
Our assessment shows that the global impact of systematic effects uncertainties in the LFI do not limit either temperature or E-mode spectra measurements.
Figure 1. Angular power spectra of the various systematic effects compared to the Planck beam-filtered temperature and polarization spectra. The dark-gray thick curve represents the total contribution. The dark-green dotted curve represent the contribution from far sidelobes that has been removed from the data and, therefore not considered in the total. The CMB TT and EE curves correspond to the Planck best-fit power spectra. The theoretical $B$-mode CMB spectrum assumes a tensor-to-scalar ratio r = 0.1, a tensor spectral index nT=0 and has not been beam-filtered. Rows: 30, 44 and 70 GHz spectra. Columns: temperature, E-mode and B-mode spectra. .
Effects independent of sky signal[edit]
Noise correlations and 1/f noise[edit]
TBW
Thermal effects[edit]
TBW
Bias fluctuations[edit]
TBW
1-Hz spikes[edit]
TBW
Main Beam Ellipticity[edit]
TBW
Near Sidelobes pickup[edit]
TBW
Effects dependent on sky signal[edit]
Sidelobe pick-up[edit]
TBW
ADC non linearity[edit]
TBW
Imperfect photometric calibration[edit]
Pointing effects[edit]
TBW
Polarization Angle Uncertainty[edit]
TBW
Ortho-Mode Transducer Cross-Polarization[edit]
TBW
References[edit]
- ↑ Jump up to: 1.01.11.2 Planck 2013 results. III. Low Frequency Instrument systematic uncertainties, Planck Collaboration, 2014, A&A, 571, A3
- Jump up ↑ HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
(Planck) Low Frequency Instrument
Cosmic Microwave background
Data Processing Center
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
analog to digital converter