Beams LFI
Contents
Overview[edit]
LFI is observing the sky with 11 pairs of beams associated with the 22 pseudo-correlation radiometers. Each beam of the radiometer pair (Radiometer Chain Assembly - RCA) is named as LFIXXM or LFIXXS. XX is the RCA number ranging from 18 to 28; M and S are the two polarization namely main-arm and side-arm of the Orthomode transducers #darcangelo2009b (see also LFI naming convention).
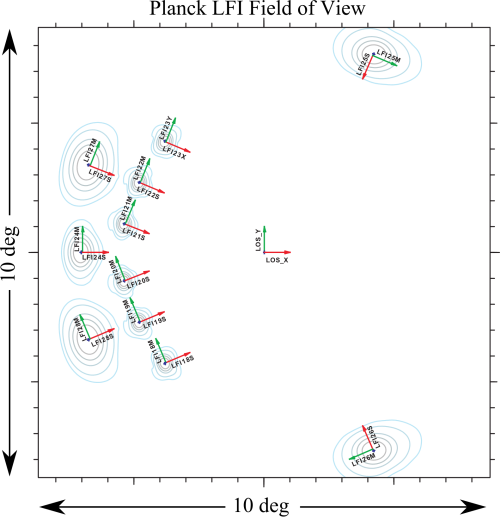
Main Beams and Focal Plane calibration[edit]
As the focal plane calibration we refer to the determination of the beam pointing parameters in the nominal Line of Sight (LOS) frame through main beam measurments using Jupiter transits. the parametes that characterise the beam pointing are the following:
- THETA_UV ($\theta_{uv}$)
- PHI_UV ($\phi_{uv}$)
They are calculated starting from u,v coordinates derived form the beam reconstruction algorithm as
$\theta_{uv} = \arcsin(u^2+v^2)$
$\phi_{uv} = \arctan(v/u)$
Two additional angles are used to characterize the beams in the RIMO:
- PSI_UV ($\psi_{uv}$)
- PSI_POL ($\psi_{pol}$)
$\psi_{uv}$ and $\psi_{pol}$ are not derived from measurements but they are extimated form optical simulations. They are the quantities that represent the polarization direction of each beam, in the following approximation: the M- and S- beams of the same RCA point at the same direction on the sky.
The main beams are characterised by 2 method:
- elliptical (or bivariate) gaussian fit as in #[planck2011-1-6] with modification explained in #[planck2013-p02d]. This method is used to determine
- the beam centre
- the average full width half maximum defined as $\sqrt{FWHM_{max}\cdot FWHM_{min}}$
- the beam ellipticity defined as $FWHM_{max}\over{FWHM_{min}}$
- the beam tilting, $\psi_{ell}$, with respect the u-axis.
- Electromagnetic simulation (using GRASP Physical Optics code) by appropriately tuning the Radio Frequency Flight Model (RFFM) #tauber2010b. The Radio Frequency Tuned Model, called RFTM, was implemented to fit the beam data with electromagnetic model. It is derived as follow:
- the Focal plane unit electromagnetic model has shifted by 3.5mm toward the secondary mirror;
- All the simulated beams where monochromatic, i.e calculated at a single frequency called Optical Center Frequency (OCF). For the RFTM model the OCF has been chosen at $28.0$, $44.0$, $70.0$. In fact the optical and radiometer bandshapes as reported in #zonca2009</zonca> demonstrates that for the 30 GHz channel, the radiometer responses are better described by a central frequency closer to 28 GHz with respect to the nominal one, whereas for the other two frequency channels the OCF is close to the nominal one.
- each feed horn phase centre has been moved alogn horn axis to optimize the match between simulations and data. The optimization was obtained by minimizing the variance according to the following definition: If $B_s[u,v]$ is the peak-normalized scanning beam matrix (for semplicity we use here $(u,v)$ coordinates also as indexes of the beam matrix) and $B_o[u,v]$ is the smeared peak-normalized simulated GRASP beam, the variance, $\sigma$, can be evaluated for each beam:
\begin{eqnarray} \label{eqsigma} \sigma &=& {\sum_{u,v}{(f[u,v] - \overline{f})^2}}\cdot {1\over N} \\ f[u,v]&=&w[u,v] \cdot (B^{dB}_s(u,v)- B^{dB}_o(u,v)) \\ w[u,v]&=&\sqrt{T[u,v]} \end{eqnarray} where also $T[u,v]$ is the temperature or the scanning beam not normalized to peak, and $N$ is the number of points considered in the comparison so that the number of point in the (u,v) plane. The parameter $\sigma$, as already said, is the variance of the difference between two beams weighted by the measured beam itself. For each beam the variance has computed computed down to $-15$dB from beam peak to avoid bias due to noise and background.
Effective beams[edit]
TBW
Window Functions[edit]
TBW
Sidelobes[edit]
There is no direct measurements of sidelobes for LFI. The sidelobe pattern is estimated by simulations taking into account the geometry of the telescope and the satellite structure. In figure
References[edit]
<biblio force=false>
</biblio>
(Planck) Low Frequency Instrument
LFI Radiometer Chain Assembly
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
Line Of Sight
reduced IMO
Full-Width-at-Half-Maximum