Map-making and photometric calibration
Contents
Introduction[edit]
This page will give an overview of the map-making and photometric calibration procedures used by the HFI DPC to build detector and frequency maps for the 2015 data release. They are described in A09 ref. These have common elements with the tools used for the 2013 release that are described in Planck-2013-VI[1] and Planck-2013-VIII[2].
To build HFI maps, we use the destriping approximation, in which noise is assumed to decompose into two components : white noise plus low frequency drifts. Using the sky redundancy, the low frequency drifts are modelled as one constant, or offset, per pointing period. To speed up the ulterior processing we first build intermediate products, by taking advantage of redundancies : we average signal and detector orientation on healpix pixels visited during each fixed pointing period, which we call hereafter 'ring'. Detector's pointing are corrected for slow drifts and aberration (displacement on the sky indouced by the satellite's motion). This intermediate product is called HPR for healpix pixel ring. They have been constructed using the same map resolution as the final HFI products (corresponding to =2048). This new dataset is used as input in the following steps.
Photometric calibration[edit]
Dipole calibration (100 to 353 GHz)[edit]
For the 2015 data release, the HFI CMB channels were calibrated using the orbital dipole modulation. This time-variable anisotropy results from the motion of the spacecraft in the solar system, which is precisely measured. Thus it provides an absolute calibrator for orbital CMB missions. Its measurement is now used to calibrate HFI data thanks to the improvements in the timne stability of the data brought by the ADC non-linearities corrections and a better control for the detectors time response.
Residual time response slow components are modeled as a dipole shifted by 90 degrees in phase, whose amplitude is fitted bolometer per bolometer. To mitigate residual systematics, we perform a simultaneous fit of the detectors gains on the orbital dipole. This amounts to solve the non-linear equation :
where d is s the detector measurement, D the total dipole component, n the (white) noise, and both S the sky signal, g the detector gain, O the offset (for ring no i) are the unknowns to be determined. This is done by linearizing it to look for gains and sky variations, and iterating by updating the approximate sky and gains.
Higher frequency calibration (545 and 857 GHz)[edit]
We therefore the sub-mm channels' calibration for the 2015 Planck data release from the comparison of measurements of the Neptune and Uranus fluxes (with aperture photometry) with their expectations from the Moreno et al model of their atmospheres' emission. This procedure is justified, since for both planets, at the lower frequencies (100-353 Ghz), the fluxes we recover are in agreement within ~ +/-5\% with what is expected from the planet spectral model, and the HFI detector's band-passes.
Zero levels[edit]
We determined zero-level for the released maps in selected regions of the sky where dust emissions are low and well correlated with HI. We may thus estimate and subtract dust emissions using the HI template, and CMB from a Planck component-separated template. The remaining astrophysical zero level is that of CIB. By imposing that the level we find is equal to that of the CIB model of Bethermin et al, we set the zero level of our maps.
Building of maps[edit]
Using the photometric calibration parameters, we build maps in two steps :
- we determine the destriping offsets using the full mission data for all detectors of a given frequency
- we build the maps, using these offsets, by inverting the photometric equation :
where d is the destriped and calibrated signal at the HPR level. Detector's data are combined with an inverse noise weights derived from each detector's NEP. Q and U maps are build whenever possible. We propagate the white noise by building the 3x3 (or 1x1 if only I is reconstructed) covariance matrices in each pixel. At each frequency we build maps combining all detectors and independent detector sets. We use the offsets build for the full mission for building maps for each scan survey, year (sombineation of surveys 1 and 2 or 3 and 4 respectively) and for the full, nominal mission duration and its two halves. We also build maps from the two independent halves of each rings. Altogether, more than 8000 maps are built at each release.
HPR and Maps are built in galactic coordinates.
Noise properties[edit]
Map noise properties can be evaluated using several methods, thanks to the high level of observation redundancies. We can use the maps built from the difference between the first and second half of each rings, or compare individual sky scans, years, half-mission or independent detector sets with each other. Some of these tests are described in A09 ref.
Low resolution (nside = 8, 16) pixel-to-pixel noise covariance matrices are build using an analytic approach from the measured noise power spectra. CONFIRM THIS.
Zodiacal light correction[edit]
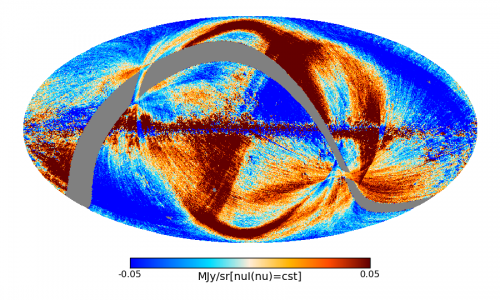
At the highest Planck frequencies, zodiacal light emission is visible in a survey difference map:
This map is a difference between the 857 GHz Survey 2 map and the 857 GHz Survey 1 map. This difference effectively removes Galactic and other emissions which originate far from Planck. As the Solar elongation is different for measurements of the same point on the sky for the two surveys, we see zodiacal light emission, while all emission from further sources is removed. The zodiacal light emission follows the Ecliptic plane, which starts at the lower left of the image, then crosses the center of the plot towards the upper right. Note that the "arcs" at the top and bottom of the image are images of the Galactic center in the Far Sidelobes, which are discussed in the section below. Similar plots for other HFI frequencies, for maps both before and after removal, are shown here.
For the 2015 Planck release, zodiacal light emission is removed from all HFI channels. It is described in Planck-2013-VI[1], but a synopsis of the procedure is as follows:
- During each survey, a large fraction of the sky has observations which all fall within a week of each other. That is, during a single survey, most pixels are observed during a short, well-defined period. The contribution from zodiacal light emission to the total brightness seen, then, is well defined.
- We use the the COBE model of the zodiacal light emission to make predictions for this zodiacal light emission for those pixels observed over a span of one week or less. The templates from the COBE model are shown here.
- We fit the survey difference maps with these model templates to estimate the emissivity of each zodi component at the Planck wavelengths. The results of these fits at each frequency are given in the Planck/HFI Map-Making paper.
- We reconstruct each ring of the the full mission using the combination of the COBE geometric model with the emissivities determined above.
- We remove the reconstruction above from each ring of data.
- We then make maps as described previously in this section.
Far SideLobes (FSL)[edit]
The far sidelobe correction for the highest frequency HFI channels is described in the section above. Note that this correction is not always used, as other, CMB-specific, component separation methods have been more effective at removing the zodiacal light emission, though as this is done along with dust and other component removal, it is difficult to characterize the zodiacal light emission in this fashion.
Fit values for specific horns and surveys are show here
We have made estimates of the contamination of the far sidelobes at 143 GHz by taking the 143 GHz map, adding the dipole, and passing it through our simulator, using a GRASP calculation of the far sidelobes for the 143-1a detector as the beam. The resulting maps is
While there is one small region that might reach 20 micro-K (this happens when the secondary spillover overlaps with the Galactic center), most of the map is quite quiet. This is evidenced by the power spectrum of the above map, which is quite small.
CO correction[edit]
The extraction of CO maps from HFI maps is described in detail in the Planck-2013-XIII[3]. The CO maps are produced by a combination of bolometer maps or frequency maps.
Map validation[edit]
Several validations of HFI maps are described in A08 ref and in A09 ref.
Further checks are presented in the likelihood, params, comsep and commander papers refs .
References[edit]
- ↑ 1.01.1 Planck 2013 results. VI. High Frequency Instrument Data Processing, Planck Collaboration, 2014, A&A, 571, A6
- ↑ Planck 2013 results. VIII. HFI photometric calibration and Map-making, Planck Collaboration, 2014, A&A, 571, A8
- ↑ Planck 2013 results. XIII. Galactic CO emission, Planck Collaboration, 2014, A&A, 571, A13
(Planck) High Frequency Instrument
Data Processing Center
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
Cosmic Microwave background
analog to digital converter
Noise Equivalent Power