HFI design, qualification, and performance
The inversion of HFI data requires that one knows how the instrument selects photons, how these photons are transformed in data transmitted by telemetry and what spurious signals are added in this process.
Contents
HFI high level description and Architecture[edit]
(Lamarre/Pajot) Should be short, understandable and point through links to the relevant sections and papers.
Cryogenics[edit]
(F .Pajot)
Dilution[edit]
(including PIDs)
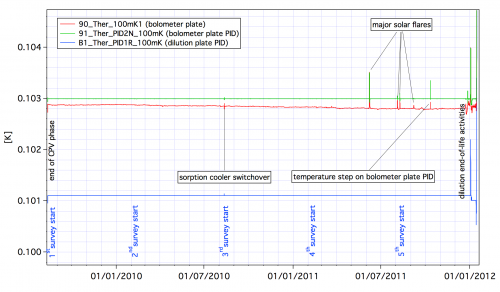
The HFI 3He-4He dilution cooler produces temperatures of 0.1 K for the bolometers through the dilution of 3He into 4He and 1.4 K through JT expansion of the 3He and 4He mixture. The dilution cooler is described in detail in section 2.3.3 of Planck early paper II .
The dilution was operated with flows set to the minimum available value, and provided a total lifetime of 30.5 months, exceeding the nominal lifetime of 16 months by 14.5 months. The dilution stage was stabilized by a PID control with a power comprised between 20 and 30 nW providing a temperature near 101 mK. The bolometer plate was stabilized at 102.8 mK with a PID power around 5 nW [fig. 100mK_stability.png].
(here a few lines of 100 mK boloplate stability)
Detailed analysis of the in-flight stability of the dilution cooler can be found in section 5.4 of Planck early paper II .
4K J-T cooler[edit]
(including PIDs for details links to the early cryogenic paper (need to add data ?))
The HFI 4K J-T cooler produces a temperature of 4K for the HFI 4K stage and optics and the precooling of the dilution gases. Full description of the 4K cooler can be found in in section 2.3.2 of Planck early paper II .
The 4K cooler was operated without interruption during all the survey phase of the mission. It is still in operation as it also provides the cooling of the optical reference loads of the LFI. The 4K PID stabilizing the temperature of the HFI optics is regulated at 4.81 K using a power around 1.8 mW [fig. 4K -A VENIR-].
(here a few lines of 4K stability, including compressors operation)
Details on the in-flight performance of the dilution cooler can be found in in section 5.3 of Planck early paper II .
Cold optics[edit]
(Lamarre)
Horns,lenses[edit]
links to Peter's paper
filters, band[edit]
Includes Locke's very detailed document.
Detection chain[edit]
(Francesco Piacentini)
Bolometers[edit]
(notes by Alain: take from DOC file (50 Mo) from Francesco, email 15 Oct 2012 17:39:03)
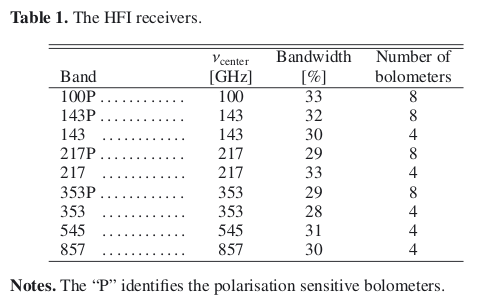
The heart of the HFI - the detectors - are bolometers, solid-state devices in which the incoming radiation dissipates its energy as heat that increases the temperature of a thermometer. The instrument Flight Model total number of bolometers is 52, split into 6 channels at central frequencies of 100, 143, 217, 353, 545, and 857GHz.
Thirty two of these bolometers are polarization sensitive allowing a map of the CMB polarisation to be built.
Bolometers consist of (i) an absorber that transforms the in-coming radiation into heat; (ii) a thermometer that is thermally linked to the absorber and measures the temperature changes; and (iii) a weak thermal link to a thermal sink, to which the bolometer is attached.
The detectors are semi-conducting NTD thermistor bolometers. There are two kinds of detector modules:
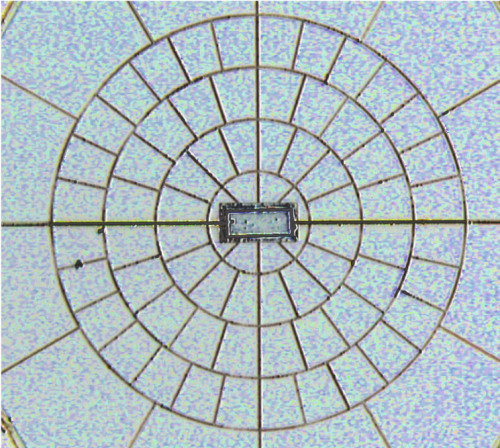
- SWB, spider web bolometers, are mounted on an absorbing spider-web of metallised silicon nitride
- PSB, polarization sensitive bolometers, are mounted or on a parallel absorbing grid of metallised silicon nitride.
In the spider-web bolometers, or SWBs (Bock et al. 1995; Mauskopf et al. 1997), the absorbers consist of metallic grids
deposited on a Si3 N4 substrate in the shape of a spider web.
The mesh design and the impedance of the metallic layer are
adjusted to match vacuum impedance and maximize the absorption of millimeter waves, while minimizing the cross section to
particles. The absorber is designed to offer equal impedance to
any linearly polarised radiation. Nevertheless, the thermometer
and its electrical leads define a privileged orientation (Fig. SWB) that
makes the SWBs slightly sensitive to polarisation, as detailed in
(Rosset et al. 2010). The thermometers are
made of neutron transmuted doped (NTD) germanium (Haller
et al. 1996), chosen to have an impedance of about 10 MΩ at
their operating temperature.
The absorber of PSBs is a rectangular grid (Fig. PSB) with metallization in one direction (Jones et al. 2003). Electrical fields parallel to this direction develop currents and then deposit some power in the grid, while perpendicular electrical fields propagate through the grid without significant interaction. A second PSB perpendicular to the first one absorbs the other polarisation. Such a PSB pair measures two polarisations of radiation collected by the same horns and filtered by the same devices, which minimises the systematic effects: differences between polarised beams collected by a given horn are typically less than −30 dB of the peak. The differences in the spectral responses of a PSB pair also proved to be a few percent in the worst case. Each pair of PSBs sharing the same horn is able to measure the intensity Stokes parameter and the Q parameter associated with its local frame. An associated pair of PSBs rotated by 45◦ scans exactly the same line (if the geometrical alignment is perfect), providing the U Stokes parameter.
The detectors operate at a temperature close to 100 mK, while the filters are distributed on the 100mK, 1.6 K,
and 4 K stages in such a way that the heat load on the coldest stages is minimized to
limit the heat load on the detectors and to decrease
the heat lift requirement and thus enhance the mission lifetime. The self-emission of the 4K stage is minimised to limit the photon noise contribution on
the detectors from the instrument.
The HFI Focal Plane Unit accommodates sub-millimiter absorbing
material in order to decrease the scattering inside it.
Insert here table 1 from HFI-Early paper http://dx.doi.org/10.1051/0004-6361/201116487http://dx.doi.org/10.1051/0004-6361/201116487 I report the table as a figure for the moment
Focal plane layout[edit]
This section may also go somewhere else, like in optics
The layout of the detectors in the focal plane is defined to cope with the
scanning strategy. The HFI horns are positioned at the centre of the focal plane, where the optical
quality is good enough for the high frequencies. The curvature of
rows compensates for the distortion of images by the telescope.
A pair of identical SWB will scan the same circle on the sky to
provide additional redundancy. Similar horns feeding PSBs are
also aligned so that two pairs of PSBs rotated by 45◦ with respect to each other scan the same line. This will provide the Q
and U Stokes parameters with minimal correction for the pointing (Rosset et al. 2010). Residual systematics will come from the differences between the beam shapes of the two horns. In all
cases except for the 100 GHz horns, a measurement is also done
by a pair of similar channels shifted by 1.25 arcminutes in the cross-scan direction, to ensure adequate sampling
. In the figures focal plane layout is reported.
Readout[edit]
[From HFI pre flight paper] The AC bias readout electronics of
the HFI instrument (Gaertner et al. 1997) includes a number of original features proposed by several laboratories (CRTBT in
Grenoble, CESR in Toulouse and IAS in Orsay), which were
validated on the Diabolo experiment and on the balloon-borne
Archeops experiment. It was developped for space by the CESR
in Toulouse.
The particular features of the HFI AC bias readout are mainly
- i)that the cold load resistors were replaced by capacitors because they have no Johnson noise;
- ii)that the detectors are
biased by applying a triangular voltage to the load capacitors which produces a square current [Ibias ] in the capacitors, and a square voltage [T bias ] that compensates for the stray capacitance of the wiring (producing a nearly square bias current into the bolometer;
- iii)that a square offset com-pensation signal is subtracted to the bolometric signal to minimise the amplitude of the signal that has to be amplified and
digitized;
- iv)that the electronic scheme is symmetrical and uses
a differential amplification scheme to optimize the immunity to electromagnetic interferences;
- v)and finally that every parameter of the REU can be set by commands, which
is made possible by using digital-to-analog and analog-to-digital converters extensively.
The readout electronics consist of 72 channels designed to perform low noise measurements of the impedance of 52 bolometers, two blind bolometers, 16 accurate low temperature thermometers, all in the 10 MΩ range, one resistor of 10 MΩ and
one capacitor of 100 pF. The semiconductor bolometers and thermometers of Planck-HFI operate at cryogenic temperature around 100 mK on the focal plane, with impedance of about 10 MΩ when biased at the optimal current. The readout electronics on the contrary have to operate at “room” temperature (300 K). The distance between the two extremities of the readout chain is about 10 m and could represent a point of extreme susceptibility to electromagnetic interference. The readout electronic chain was split into three boxes. These are the JFET box, located on the 50 K stage of the satellite at 2.2 m from the focal plane, the pre-amplifier unit (PAU), located 1.8m further at 300 K, and the REU, located on the opposite side of the satellite, 5 m away. Each of the three boxes (JFET, PAU and REU) consists of 12 belts of six channels. The first nine belts are dedicated to the bolometers, and the three last ones to the accurate thermometers, the resistor and the capacitor (see figure Organization of the HFI readout).
Illustration 6: Organization of the HFI readout. Each row represents a belt. Each belt has 6 channels.
Principles of the readout electronics.[edit]
From HFI pre-flight paper
See figure [Principles of readout electronics]. The bolometer is biased by a square wave AC current obtained by the differentiation of a triangular voltage through a load capacitance, in a completely differential architecture. The presence of the stray capacitance due to losses of charge in the
wiring requires a correction of the shape of the square bias current by a transient voltage. Thus the bias voltage generation is controlled by the two parameters I-bias and T-bias that express the amplitude of the triangular and transient voltage. The compensation voltage added to the bolometric signal to optimize the dynamic of the chain is controlled by the V-bal parameter.
Illustration 6: Principles of readout electronics. The three modules of the chain are shown: JFet Box, Pre-Amplifier
Unit (PAU) and Readout Electronic Unit (REU).
Parameters of the Readout Unit can be set to optimize the detectors performance.
The modulation frequency of the AC bias system, fmod of the square bias current
can be tuned from 70 Hz to 112 Hz by the telecommand parameters:
Nsample, which defines the number of samples per
half period of modulated signal,
fdiv which determines
the sampling frequency of the ADC.
The optimal frequencies
are around 90 Hz.
Each channel has its own settings for the following parameters: I-bias, amplitude of the triangular bias voltage;
T-bias, amplitude of the transient bias voltage;
V-bal, amplitude of the square compensation voltage;
G-amp, value of the programmable gain of the REU [1/3, 1,
3, 7.6];
N-blank, number of blanked samples at the beginning of halfperiod not taken into account during integration of the signal;
S-phase, phase shift when computing the integrated signal.
All these parameters influence the effective response of the detection chains, and were optimized during the calibration campaigns and confirmed during the calibration and
performance verification (CPV) phase following the launch of
Planck. The scientific signal is provided by the integral of the
signal on each half-period, between limits fixed by the S-phase
and N-blank parameters.
The interaction of modulated readout electronics with semiconductor bolometers is rather different from that of a classical
DC bias readout (Jones 1953). The differences were seen during the calibration of the HFI, although the readout electronics was designed to mimic the operation of a DC biased bolometric system as far as possible. With the AC readout the maximum of responsivity is lower and is obtained for higher bias current in the bolometer with respect to the DC model. This is caused by the stray capacitance in the wiring which has negligible effects for a DC bias and a major effect for an AC bias. In our case, a stray capacitance of 150 pF induces increases of NEP ranging from 4% (857 GHz bolometers) to 10% (100 GHz bolometers) and also affects the HFI time response. Details of the effect of the HFI AC bias system into the time response of the detectors are discussed in the Time Response Section [link].
[Here I suggest to copy the wiki post with in flight setting of parameters http://wiki.planck.fr/index.php/Proc/HFIstatehttp://wiki.planck.fr/index.php/Proc/HFIstate Or a table with the physical values. I have an excel file prepared by F-X Desert]
JFETs[edit]
Taken from pre-flight paper
Given the high impedance of the bolometers and the length of the connecting cables, it it is essential that the impedance of the signal is lowered as close as possible to the detectors. In our system this is accomplished
by means of JFET source followers, located in boxes connected to the 50 K stage.
There are two JFETs per channel, since the readout is fully differential, and they provide a current amplification of the signal while keeping the voltage amplification very close to unity.
Inside the box, the JFETs are
mounted on a thermally insulated plate with an active temperature control to keep them at the optimal temperature of 110 K.
With a dissipated power lower than 240 mW,
mainly produced by the JFETs and the source resistors, we obtained a noise power spectral density of less than 3 nV Hz1/2 for
the frequency range of interest. This increases the total noise of
all bolometer channels by less than 5%.
Data compression[edit]
Time response.[edit]
The HFI bolometers and readout electronics have a finite response time to changes in incident optical power. The bolometers are thermal detectors of radiation whose response time is determined by the thermal circuit defined by the heat capacity of the detector and thermal conductivity.
Due to Planck's nearly constant scan rate, the time response is degenerate with the optical beam. However, because of the long time scale effects present in the time response, the time response is deconvolved from the data in the processing of the HFI data (see TOI processing).
The time response of the HFI bolometers and readout electronics is modeled as a Fourier domain transfer function (called the LFER4 model) consisting of the product of an bolometer thermal response and an electronics response .
LFER4 model[edit]
If we write the input signal (power) on a bolometer as the bolometer physical impedance can be written as: where is the angular frequency of the signal and is the complex intrinsic bolometer transfer function. For HFI the bolometer transfer function is modelled as the sum of 4 single pole low pass filters: The modulation of the signal is done with a square wave, written here as a composition of sine waves of decreasing amplitude: where we have used the Euler relation and is the angular frequency of the square wave. The modulation frequency is and was set to Hz in flight. This signal is then filtered by the complex electronic transfer function . Setting: we have: This signal is then sampled at high frequency (). is one of the parameters of the HFI electronics and corresponds to the number of high frequency samples in each modulation semi-period. In order to obtain an output signal sampled every seconds, we must integrate on a semiperiod, as done in the HFI readout. To also include a time shift , the integral is calculated between and (with period of the modulation). The time shift is encoded in the HFI electronics by the parameter , with the relation .
After integration, the -sample of a bolometer can be written as where
The output signal in equation eqn:output can be demodulated (thus removing the ) and compared to the input signal in equation bol_in. The overall transfer function is composed of the bolometer transfer function and the effective electronics transfer function, :
The shape of is obtained combining low and high-pass filters with Sallen Key topologies (with their respective time constants) and accounting also for the stray capacitance low pass filter given by the bolometer impedance combined with the stray capacitance of the cables. The sequence of filters that define the electronic band-pass function are listed in table table:readout_electronics_filters.
Parameters of LFER4 model[edit]
The LFER4 model has are a total of 10 parameters(,,,,,,,,,) 9 of which are independent, for each bolometer. The free parameters of the LFER4 model are determined using in-flight data in the following ways:
- is fixed at the value of the REU setting.
- is measured during the QEC test during CPV.
- , , , are fit forcing the compactness of the scanning beam.
- , , are fit by forcing agreement of survey 2 and survey 1 maps.
- The overall normalization of the LFER4 model is forced to be 1.0 at the signal frequency of the dipole.
The details of determining the model parameters are given in (reference P03c paper) and the best-fit parameters listed here in table table:LFER4pars.
HFI electronics filter sequence[edit]
| Filter | Parameters | Function |
|---|---|---|
| 0. Stray capacitance low pass filter | ||
| 1. Low pass filter | k nF |
|
| 2. Sallen Key high pass filter | k |
3 |
| 3. Sign reverse with gain | ||
| 4. Single pole low pass filter with gain | k nF |
|
| 5. Single pole high pass filter coupled to a Sallen Key low pass filter | k k nF k F |
| Bolometer | (s) | (s) | (s) | (s) | (s) | |||||
| 100-1a | 0.392 | 0.01 | 0.534 | 0.0209 | 0.0656 | 0.0513 | 0.00833 | 0.572 | 0.00159 | 0.00139 |
| 100-1b | 0.484 | 0.0103 | 0.463 | 0.0192 | 0.0451 | 0.0714 | 0.00808 | 0.594 | 0.00149 | 0.00139 |
| 100-2a | 0.474 | 0.00684 | 0.421 | 0.0136 | 0.0942 | 0.0376 | 0.0106 | 0.346 | 0.00132 | 0.00125 |
| 100-2b | 0.126 | 0.00584 | 0.717 | 0.0151 | 0.142 | 0.0351 | 0.0145 | 0.293 | 0.00138 | 0.00125 |
| 100-3a | 0.744 | 0.00539 | 0.223 | 0.0147 | 0.0262 | 0.0586 | 0.00636 | 0.907 | 0.00142 | 0.00125 |
| 100-3b | 0.608 | 0.00548 | 0.352 | 0.0155 | 0.0321 | 0.0636 | 0.00821 | 0.504 | 0.00166 | 0.00125 |
| 100-4a | 0.411 | 0.0082 | 0.514 | 0.0178 | 0.0581 | 0.0579 | 0.0168 | 0.37 | 0.00125 | 0.00125 |
| 100-4b | 0.687 | 0.0113 | 0.282 | 0.0243 | 0.0218 | 0.062 | 0.00875 | 0.431 | 0.00138 | 0.00139 |
| 143-1a | 0.817 | 0.00447 | 0.144 | 0.0121 | 0.0293 | 0.0387 | 0.0101 | 0.472 | 0.00142 | 0.00125 |
| 143-1b | 0.49 | 0.00472 | 0.333 | 0.0156 | 0.134 | 0.0481 | 0.0435 | 0.27 | 0.00149 | 0.00125 |
| 143-2a | 0.909 | 0.0047 | 0.0763 | 0.017 | 0.00634 | 0.1 | 0.00871 | 0.363 | 0.00148 | 0.00125 |
| 143-2b | 0.912 | 0.00524 | 0.0509 | 0.0167 | 0.0244 | 0.0265 | 0.0123 | 0.295 | 0.00146 | 0.00125 |
| 143-3a | 0.681 | 0.00419 | 0.273 | 0.00956 | 0.0345 | 0.0348 | 0.0115 | 0.317 | 0.00145 | 0.00125 |
| 143-3b | 0.82 | 0.00448 | 0.131 | 0.0132 | 0.0354 | 0.0351 | 0.0133 | 0.283 | 0.00161 | 0.000832 |
| 143-4a | 0.914 | 0.00569 | 0.072 | 0.0189 | 0.00602 | 0.0482 | 0.00756 | 0.225 | 0.00159 | 0.00125 |
| 143-4b | 0.428 | 0.00606 | 0.508 | 0.00606 | 0.0554 | 0.0227 | 0.00882 | 0.084 | 0.00182 | 0.00125 |
| 143-5 | 0.491 | 0.00664 | 0.397 | 0.00664 | 0.0962 | 0.0264 | 0.0156 | 0.336 | 0.00202 | 0.00139 |
| 143-6 | 0.518 | 0.00551 | 0.409 | 0.00551 | 0.0614 | 0.0266 | 0.0116 | 0.314 | 0.00153 | 0.00111 |
| 143-7 | 0.414 | 0.00543 | 0.562 | 0.00543 | 0.0185 | 0.0449 | 0.00545 | 0.314 | 0.00186 | 0.00139 |
| 217-5a | 0.905 | 0.00669 | 0.0797 | 0.0216 | 0.00585 | 0.0658 | 0.00986 | 0.342 | 0.00157 | 0.00111 |
| 217-5b | 0.925 | 0.00576 | 0.061 | 0.018 | 0.00513 | 0.0656 | 0.0094 | 0.287 | 0.00187 | 0.00125 |
| 217-6a | 0.844 | 0.00645 | 0.0675 | 0.0197 | 0.0737 | 0.0316 | 0.0147 | 0.297 | 0.00154 | 0.00125 |
| 217-6b | 0.284 | 0.00623 | 0.666 | 0.00623 | 0.0384 | 0.024 | 0.0117 | 0.15 | 0.00146 | 0.00111 |
| 217-7a | 0.343 | 0.00548 | 0.574 | 0.00548 | 0.0717 | 0.023 | 0.0107 | 0.32 | 0.00152 | 0.00139 |
| 217-7b | 0.846 | 0.00507 | 0.127 | 0.0144 | 0.0131 | 0.0479 | 0.0133 | 0.311 | 0.00151 | 0.00139 |
| 217-8a | 0.496 | 0.00722 | 0.439 | 0.00722 | 0.0521 | 0.0325 | 0.0128 | 0.382 | 0.00179 | 0.00111 |
| 217-8b | 0.512 | 0.00703 | 0.41 | 0.00703 | 0.0639 | 0.0272 | 0.0139 | 0.232 | 0.00173 | 0.00125 |
| 217-1 | 0.0136 | 0.00346 | 0.956 | 0.00346 | 0.0271 | 0.0233 | 0.00359 | 1.98 | 0.00159 | 0.00111 |
| 217-2 | 0.978 | 0.00352 | 0.014 | 0.0261 | 0.00614 | 0.042 | 0.00194 | 0.686 | 0.0016 | 0.00125 |
| 217-3 | 0.932 | 0.00355 | 0.0336 | 0.00355 | 0.0292 | 0.0324 | 0.00491 | 0.279 | 0.00174 | 0.00125 |
| 217-4 | 0.658 | 0.00135 | 0.32 | 0.00555 | 0.0174 | 0.0268 | 0.00424 | 0.473 | 0.00171 | 0.00111 |
| 353-3a | 0.554 | 0.00704 | 0.36 | 0.00704 | 0.0699 | 0.0305 | 0.0163 | 0.344 | 0.0017 | 0.00125 |
| 353-3b | 0.219 | 0.00268 | 0.671 | 0.00695 | 0.0977 | 0.0238 | 0.0119 | 0.289 | 0.00157 | 0.00111 |
| 353-4a | 0.768 | 0.00473 | 0.198 | 0.00993 | 0.0283 | 0.0505 | 0.00628 | 0.536 | 0.00181 | 0.00125 |
| 353-4b | 0.684 | 0.00454 | 0.224 | 0.0108 | 0.0774 | 0.08 | 0.0149 | 0.267 | 0.00166 | 0.00111 |
| 353-5a | 0.767 | 0.00596 | 0.159 | 0.0124 | 0.0628 | 0.0303 | 0.0109 | 0.357 | 0.00156 | 0.00111 |
| 353-5b | 0.832 | 0.00619 | 0.126 | 0.0111 | 0.0324 | 0.035 | 0.0096 | 0.397 | 0.00166 | 0.00111 |
| 353-6a | 0.0487 | 0.00176 | 0.855 | 0.006 | 0.0856 | 0.0216 | 0.0105 | 0.222 | 0.00199 | 0.00125 |
| 353-6b | 0.829 | 0.00561 | 0.127 | 0.00561 | 0.0373 | 0.0252 | 0.00696 | 0.36 | 0.00228 | 0.00111 |
| 353-1 | 0.41 | 0.000743 | 0.502 | 0.00422 | 0.0811 | 0.0177 | 0.0063 | 0.329 | 0.00132 | 0.00097 |
| 353-2 | 0.747 | 0.00309 | 0.225 | 0.00726 | 0.0252 | 0.0447 | 0.00267 | 0.513 | 0.00154 | 0.00097 |
| 353-7 | 0.448 | 0.0009 | 0.537 | 0.0041 | 0.0122 | 0.0273 | 0.00346 | 0.433 | 0.00178 | 0.00125 |
| 353-8 | 0.718 | 0.00223 | 0.261 | 0.00608 | 0.0165 | 0.038 | 0.00408 | 0.268 | 0.00177 | 0.00111 |
| 545-1 | 0.991 | 0.00293 | 0.00743 | 0.026 | 0.00139 | 2.6 | 0 | 0 | 0.00216 | 0.00111 |
| 545-2 | 0.985 | 0.00277 | 0.0128 | 0.024 | 0.00246 | 2.8 | 0 | 0 | 0.00187 | 0.00097 |
| 545-4 | 0.972 | 0.003 | 0.0277 | 0.025 | 0.000777 | 2.5 | 0 | 0 | 0.00222 | 0.00111 |
| 857-1 | 0.974 | 0.00338 | 0.0229 | 0.025 | 0.00349 | 2.2 | 0 | 0 | 0.00176 | 0.00111 |
| 857-2 | 0.84 | 0.00148 | 0.158 | 0.00656 | 0.00249 | 3.2 | 0 | 0 | 0.0022 | 0.00125 |
| 857-3 | 0.36 | 4.22e-05 | 0.627 | 0.0024 | 0.0111 | 0.017 | 0.002 | 1.9 | 0.00152 | 0.00126 |
| 857-4 | 0.278 | 0.0004 | 0.719 | 0.00392 | 0.00162 | 0.09 | 0.00152 | 0.8 | 0.00149 | 0.000558 |
System (Ken)[edit]
List of systematics[edit]
Like all experiments, Planck/HFI had a number of "issues" which it needed to track and verify were not compromising the data. While these are discussed in appropriate sections, here we gather them together to give brief summaries of the issues and refer the reader to the appropriate section for more details.
- Cosmic Rays - Unprotected by the atmosphere and more sensitive than previous bolometric experiment, HFI was subjected to many more cosmic ray hits than previous experiments. These were detected, the worst parts of the data flagged as unusable, and "tails" were modeled and removed. This is described in XXXXX
- Elephants - Cosmic rays also hit the 100 mK stage and cause the temperature to vary, inducing small temperature and thus noise variations in the detectors. This is described in XXXXX
- 1.6 K Stage Fluctuations
- 4 K Stage Fluctuations
- Popcorn Noise - Some channels were occasionally affected by what seems to be a "split-level" noise, which has been variously called popcorn noise or random telegraphic signal. These data are usually flagged. This is described in XXXXX
- Jumps - Similar to but distinct from popcorn noise, small jumps were occasionally found in the data streams. These data are usually corrected. This is described in XXXXX.
- 4 K Cooler-Induced EM Noise - The 4 K cooler induced noise in the detectors with very specific frequency signatures, which is filtered. This is described in XXXXX.
- 4 K Cooler-Induced Microphonics - The mechanical cooler was shown in XXXXX to cause very little microphonic parasites in the detector data.
- Pointing-Change Microphonics - The changes in pointing after each pointing period were shown in XXXXX to cause very little microphonic parasitic signal in the detector data.
- Compression - Onboard compression is used to overcome our telemetry bandwidth limitations. This is explained in XXXXX.
- Noise Correlations - Correlations in noise between detectors seems to be negligble but for two polarization sensitive detectors in the same horn. This is discussed in XXXXX.
- Electrical Cross-Talk - Cross-talk is discussed in XXXXX.
- Pointing - The final pointing reconstruction for Planck is near the arcsecond level. This is discussed in XXXXX.
- Focal Plane Geometry - The relative positions of different horns in the focal plane is reconstructed using planets. This is discussed in XXXXX.
- Main Beam - The main beams for HFI are discussed in XXXXX.
- Ruze Envelope - Random imperfections or dust on the mirrors can increase the size of the beam a bit. This is discussed in XXXXX.
- Dimpling - The mirror support structure causes a pattern of small imperfections in the beams, which cause small sidelobe responses outside the main beam. This is discussed in XXXXX.
- Far Sidelobes - Small amounts of light can sometimes hit the detectors from just above the primary or secondary mirrors, or even from reflecting off the baffles. While small, when the Galactic center is in the right position, this can be detected in the highest frequency channels, so this is removed from the data. This is discussed in XXXXX.
- Planet Fluxes - Comparing the known fluxes of planets with the calibration on the CMB dipole is a useful check of calibration. This is done in XXXXX.
- Point Source Fluxes - As with planet fluxes, we also compare fluxes of known, bright point sources with the CMB dipole calibration. This is done in XXXXX.
- Time Constants - The HFI bolometers do not react instantaneously to light; there are small time constants, discussed XXXXX.
- ADC Correction - The HFI Analog-to-Digital Converters are not perfect, and are not used perfectly. Their effects on the calibration are discussed in XXXXX.
- Gain changes with Temperature Changes
- Optical Cross-Talk - This is discussed in XXXXX.
- Bandpass - The transmission curves, or "bandpass" has shown up in a number of places. This is discussed in XXXXX and YYYYY.
- Saturation - While this is mostly an issue only for Jupiter observations, it should be remembered that the HFI detectors cannot observe arbitrarily bright objects. This is discussed in XXXXX.
Summary[edit]
(Lamarre) here remind worse sytematics and point to DPC Summary of sucess and limitations. JML. Link to early HFI in flight perf.
(Planck) High Frequency Instrument
(Planck) Low Frequency Instrument
Cosmic Microwave background
Readout Electronic Unit
Junction Field Elect Transistor
Pre_Amplification Unit
analog to digital converter
Calibration and Performance Verification
Noise Equivalent Power
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
Data Processing Center