HFI design, qualification, and performance

The inversion of HFI data requires that one knows how the instrument selects photons, how these photons are transformed in data transmitted by telemetry and what spurious signals are added in this process.

HFI high level description and Architecture

(Lamarre/Pajot) Should be short, understandable and point through links to the relevant sections and papers.

Cryogenics

(F .Pajot)

Dilution

(including PIDs)

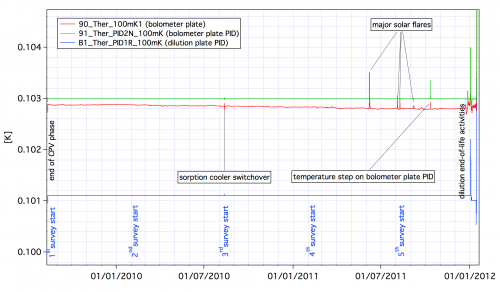
The HFI 3He-4He dilution cooler produces temperatures of 0.1 K for the bolometers through the dilution of 3He into 4He and 1.4 K through JT expansion of the 3He and 4He mixture. The dilution cooler is described in detail in section 2.3.3 of Planck early paper II .

The dilution was operated with flows set to the minimum available value, and provided a total lifetime of 30.5 months, exceeding the nominal lifetime of 16 months by 14.5 months. The dilution stage was stabilized by a PID control with a power comprised between 20 and 30 nW providing a temperature near 101 mK. The bolometer plate was stabilized at 102.8 mK with a PID power around 5 nW [fig. 100mK_stability.png].

(here a few lines of 100 mK boloplate stability)

Detailed analysis of the in-flight stability of the dilution cooler can be found in section 5.4 of Planck early paper II .

4K J-T cooler

(including PIDs for details links to the early cryogenic paper (need to add data ?))

The HFI 4K J-T cooler produces a temperature of 4K for the HFI 4K stage and optics and the precooling of the dilution gases. Full description of the 4K cooler can be found in in section 2.3.2 of Planck early paper II .

The 4K cooler was operated without interruption during all the survey phase of the mission. It is still in operation as it also provides the cooling of the optical reference loads of the LFI. The 4K PID stabilizing the temperature of the HFI optics is regulated at 4.81 K using a power around 1.8 mW [fig. 4K -A VENIR-].

(here a few lines of 4K stability, including compressors operation)

Details on the in-flight performance of the dilution cooler can be found in in section 5.3 of Planck early paper II .

Cold optics

(Lamarre)

Horns,lenses

links to Peter's paper

filters, band

Includes Locke's very detailed document.

Detection chain

(Francesco Piacentini)

Bolometers

(notes by Alain: take from DOC file (50 Mo) from Francesco, email 15 Oct 2012 17:39:03)

The heart of the HFI - the detectors - are bolometers, solid-state devices in which the

incoming radiation dissipates its energy as heat that increases the temperature of a
thermometer. The instrument Flight Model total number of bolometers is 52, split into 6
channels at central frequencies of 100, 143, 217, 353, 545, and 857GHz.

Thirty two of these

bolometers are polarization sensitive allowing a map of the CMB polarisation to be
built.

Bolometers consist of (i) an absorber that transforms the in-coming radiation into heat; (ii) a thermometer that is thermally

linked to the absorber and measures the temperature changes;
and (iii) a weak thermal link to a thermal sink, to which the
bolometer is attached.

The detectors are semi-conducting NTD thermistor bolometers. There are two kinds of detector modules:

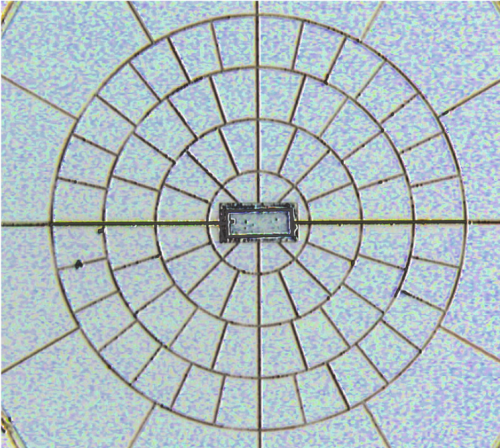
• SWB, spider web bolometers, are mounted on an absorbing spider-web of metallised silicon nitride
• PSB, polarization sensitive bolometers, are mounted or on a parallel

absorbing grid of metallised silicon nitride.

In the spider-web bolometers, or SWBs (Bock et al. 1995; Mauskopf et al. 1997), the absorbers consist of metallic grids

deposited on a Si3 N4 substrate in the shape of a spider web.
The mesh design and the impedance of the metallic layer are
adjusted to match vacuum impedance and maximise the absorption of millimetre waves, while minimising the cross section to
particles. The absorber is designed to offer equal impedance to
any linearly polarised radiation. Nevertheless, the thermometer
and its electrical leads define a privileged orientation (Fig. SWB) that
makes the SWBs slightly sensitive to polarisation, as detailed in
(Rosset et al. 2010). The thermometers are
made of neutron transmuted doped (NTD) germanium (Haller

et al. 1996), chosen to have an impedance of about 10 MΩ at

their operating temperature.

The absorber of PSBs is a rectangular grid (Fig. PSB) with metallization in one direction (Jones et al. 2003). Electrical fields

parallel to this direction develop currents and then deposit some
power in the grid, while perpendicular electrical fields propagate through the grid without significant interaction. A second
PSB perpendicular to the first one absorbs the other polarisation.
Such a PSB pair measures two polarisations of radiation collected by the same horns and filtered by the same devices, which
minimises the systematic effects: differences between polarised
beams collected by a given horn are typically less than −30 dB of
the peak. The differences in the spectral responses of a PSB pair
also proved to be a few percent in the worst case. Each pair
of PSBs sharing the same horn is able to measure the intensity
Stokes parameter and the Q parameter associated with its local
frame. An associated pair of PSBs rotated by 45◦ scans exactly
the same line (if the geometrical alignment is perfect), providing
the U Stokes parameter.

Time response.

The HFI bolometers and readout electronics have a finite response time to changes in incident optical power. The bolometers are thermal detectors of radiation whose response time is determined by the thermal circuit defined by the heat capacity of the detector and thermal conductivity.

Due to Planck's nearly constant scan rate, the time response is degenerate with the optical beam. However, because of the long time scale effects present in the time response, the time response is deconvolved from the data in the processing of the HFI data (see TOI processing).

The time response of the HFI bolometers and readout electronics is modeled as a Fourier domain transfer function (called the LFER4 model) consisting of the product of an bolometer thermal response [math]F(\omega)[/math] and an electronics response [math]H'(\omega)[/math].

[math]\label{LFER4def}TF^{LFER4}(\omega) = F(\omega) H'(\omega)[/math]

LFER4 model

If we write the input signal (power) on a bolometer as [math]\label{bol_in} s_0(t)=e^{i\omega t} [/math] the bolometer physical impedance can be written as: [math]\label{bol_out} s(t)=e^{i\omega t}F(\omega) [/math] where [math]\omega[/math] is the angular frequency of the signal and [math]F(\omega)[/math] is the complex intrinsic bolometer transfer function. For HFI the bolometer transfer function is modelled as the sum of 4 single pole low pass filters: [math]\label{bol_tf} F(\omega) = \sum_{i=0,4} \frac{a_i}{1 + i\omega\tau_i} [/math] The modulation of the signal is done with a square wave, written here as a composition of sine waves of decreasing amplitude: [math]\label{sigmod} s'(t)=e^{i\omega t}F(\omega)\sum_{k=0}^{\infty} \frac{e^{i\omega_r(2k+1)t}-e^{-i\omega_r(2k+1)t}}{2i(2k+1)} [/math] where we have used the Euler relation [math]\sin x=(e^{ix}-e^{-ix})/2i[/math] and [math]\omega_r[/math] is the angular frequency of the square wave. The modulation frequency is [math]f_{mod} = \omega_r/2\pi[/math] and was set to [math]f_{mod} = 90.18759 [/math]Hz in flight. This signal is then filtered by the complex electronic transfer function [math]H(\omega)[/math]. Setting: [math]\omega_k^+=\omega+(2k+1)\omega_r[/math] [math]\omega_k^-=\omega-(2k+1)\omega_r[/math] we have: [math]\label{sigele} \Sigma(t)=\sum_{k=0}^\infty\frac{F(\omega)}{2i(2k+1)}\left[H(\omega_k^+)e^{i\omega_k^+t}-H(\omega_k^-)e^{i\omega_k^-t}\right] [/math] This signal is then sampled at high frequency ([math]2 f_{mod} NS[/math]). [math]NS[/math] is one of the parameters of the HFI electronics and corresponds to the number of high frequency samples in each modulation semi-period. In order to obtain an output signal sampled every [math]\pi/\omega_r[/math] seconds, we must integrate on a semiperiod, as done in the HFI readout. To also include a time shift [math]\Delta t[/math], the integral is calculated between [math]n\pi/\omega_r+\Delta t[/math] and [math](n+1)\pi/\omega_r+\Delta t[/math] (with [math]T=2 \pi/\omega_r[/math] period of the modulation). The time shift [math]\Delta t[/math] is encoded in the HFI electronics by the parameter [math]S_{phase}[/math], with the relation [math]\Delta t = S_{phase}/NS/f_{mod} [/math].

After integration, the [math]n[/math]-sample of a bolometer can be written as [math]\label{eqn:output} Y(t_n) = (-1)^n F(\omega) H'(\omega) e^{i t_n \omega} [/math] where [math]\label{tfele} H'(\omega) = \frac 12 \sum_{k=0}^\infty e^{-i(\frac{\pi\omega}{2\omega_r}+\omega\Delta t)} \Bigg[ \frac{H(\omega_k^+)e^{i\omega_k^+ \Delta t}}{(2k+1)\omega_k^+} \left(1-e^{\frac{i\omega_k^+\pi}{\omega_r}}\right) \\ - \frac{H(\omega_k^-)e^{i\omega_k^- \Delta t}}{(2k+1)\omega_k^-} \left(1-e^{\frac{i\omega_k^-\pi}{\omega_r}}\right) \Bigg] [/math]

The output signal in equation eqn:output can be demodulated (thus removing the [math](-1)^n[/math]) and compared to the input signal in equation bol_in. The overall transfer function is composed of the bolometer transfer function and the effective electronics transfer function, [math]H'(\omega)[/math]: [math]TF(\omega) = F(\omega) H'(\omega) [/math]

The shape of [math]H(\omega)[/math] is obtained combining low and high-pass filters with Sallen Key topologies (with their respective time constants) and accounting also for the stray capacitance low pass filter given by the bolometer impedance combined with the stray capacitance of the cables. The sequence of filters that define the electronic band-pass function [math]H(\omega) = h_0*h_1*h_2*h_3*h_4*h_{5}[/math] are listed in table table:readout_electronics_filters.

Parameters of LFER4 model

The LFER4 model has are a total of 10 parameters([math]A_1[/math],[math]A_2[/math],[math]A_3[/math],[math]A_4[/math],[math]\tau_1[/math],[math]\tau_2[/math],[math]\tau_3[/math],[math]\tau_4[/math],[math]S_{phase}[/math],[math]\tau_{stray}[/math]) 9 of which are independent, for each bolometer. The free parameters of the LFER4 model are determined using in-flight data in the following ways:

• [math]S_{phase}[/math] is fixed at the value of the REU setting.
• [math]\tau_{stray}[/math] is measured during the QEC test during CPV.
• [math]A_1[/math], [math]\tau_1[/math], [math]A_2[/math], [math]\tau_2[/math] are fit forcing the compactness of the scanning beam.
• [math]A_3[/math], [math]\tau_3[/math], [math]A_{4}[/math] [math]\tau_4[/math] are fit by forcing agreement of survey 2 and survey 1 maps.
• The overall normalization of the LFER4 model is forced to be 1.0 at the signal frequency of the dipole.

The details of determining the model parameters are given in (reference P03c paper) and the best-fit parameters listed here in table table:LFER4pars.

HFI electronics filter sequence

HFI electronics filter sequence. We define $s = i \omega$

Filter	Parameters	Function
0. Stray capacitance low pass filter	[math]\tau_{stray}= R_{bolo} C_{stray}[/math]	[math]h_0 = \frac{1}{1.0+\tau_{stray}*s}[/math]
1. Low pass filter	[math]R_1=1[/math]k[math]\Omega[/math] [math]C_1=100[/math]nF	[math]h_1 = \frac{2.0+R_1*C_1*s}{2.0*(1.0+R_1*C_1*s)}[/math]
2. Sallen Key high pass filter	[math]R_2=51[/math]k[math]\Omega[/math] [math]C_2=1\mu[/math]	[math]h_2= \frac{(R_2*C_2*s)^2}{(1.0+R_2*C_2*s)^2}[/math]3
3. Sign reverse with gain		[math]h_3=-5.1[/math]
4. Single pole low pass filter with gain	[math]R_4=10[/math]k[math]\Omega[/math] [math]C_4=10[/math]nF	[math]h_4= \frac{1.5}{1.0+R_4*C_4*s}[/math]
5. Single pole high pass filter coupled to a Sallen Key low pass filter	[math]R_9=18.7[/math]k[math]\Omega[/math] [math]R_{12}=37.4[/math]k[math]\Omega[/math] [math]C=10.0[/math]nF [math]R_{78}=510[/math]k[math]\Omega[/math] [math]C_{18}=1.0\mu[/math]F [math]K_3 = R_9^2*R_{78}*R_{12}^2*C^2*C_{18}[/math] [math]K_2 = R_9*R_{12}^2*R_{78}*C^2+R_{9}^2*R_{12}^2*C^2+R_9*R_{12}^2*R_{78}*C_{18}*C[/math] [math]K_1 =R_9*R_{12}^2*C+R_{12}*R_{78}*R_9*C_{18}[/math]	[math]h_{5} = \frac{2.0*R_{12}*R_9*R_{78}*C_{18}*s}{s^3*K_3 + s^2*K_2+ s*K_1 + R_{12}*R_9 } [/math]

Parameters for LFER4 model.

Bolometer	[math]A_1[/math]	[math]\tau_1[/math] (s)	[math]A_2[/math]	[math]\tau_2[/math] (s)	[math]A_3[/math]	[math]\tau_3[/math] (s)	[math]A_4[/math]	[math]\tau_4[/math] (s)	[math]\tau_{stray}[/math] (s)	[math]S_{phase}[/math]
100-1a	0.392	0.01	0.534	0.0209	0.0656	0.0513	0.00833	0.572	0.00159	0.00139
100-1b	0.484	0.0103	0.463	0.0192	0.0451	0.0714	0.00808	0.594	0.00149	0.00139
100-2a	0.474	0.00684	0.421	0.0136	0.0942	0.0376	0.0106	0.346	0.00132	0.00125
100-2b	0.126	0.00584	0.717	0.0151	0.142	0.0351	0.0145	0.293	0.00138	0.00125
100-3a	0.744	0.00539	0.223	0.0147	0.0262	0.0586	0.00636	0.907	0.00142	0.00125
100-3b	0.608	0.00548	0.352	0.0155	0.0321	0.0636	0.00821	0.504	0.00166	0.00125
100-4a	0.411	0.0082	0.514	0.0178	0.0581	0.0579	0.0168	0.37	0.00125	0.00125
100-4b	0.687	0.0113	0.282	0.0243	0.0218	0.062	0.00875	0.431	0.00138	0.00139
143-1a	0.817	0.00447	0.144	0.0121	0.0293	0.0387	0.0101	0.472	0.00142	0.00125
143-1b	0.49	0.00472	0.333	0.0156	0.134	0.0481	0.0435	0.27	0.00149	0.00125
143-2a	0.909	0.0047	0.0763	0.017	0.00634	0.1	0.00871	0.363	0.00148	0.00125
143-2b	0.912	0.00524	0.0509	0.0167	0.0244	0.0265	0.0123	0.295	0.00146	0.00125
143-3a	0.681	0.00419	0.273	0.00956	0.0345	0.0348	0.0115	0.317	0.00145	0.00125
143-3b	0.82	0.00448	0.131	0.0132	0.0354	0.0351	0.0133	0.283	0.00161	0.000832
143-4a	0.914	0.00569	0.072	0.0189	0.00602	0.0482	0.00756	0.225	0.00159	0.00125
143-4b	0.428	0.00606	0.508	0.00606	0.0554	0.0227	0.00882	0.084	0.00182	0.00125
143-5	0.491	0.00664	0.397	0.00664	0.0962	0.0264	0.0156	0.336	0.00202	0.00139
143-6	0.518	0.00551	0.409	0.00551	0.0614	0.0266	0.0116	0.314	0.00153	0.00111
143-7	0.414	0.00543	0.562	0.00543	0.0185	0.0449	0.00545	0.314	0.00186	0.00139
217-5a	0.905	0.00669	0.0797	0.0216	0.00585	0.0658	0.00986	0.342	0.00157	0.00111
217-5b	0.925	0.00576	0.061	0.018	0.00513	0.0656	0.0094	0.287	0.00187	0.00125
217-6a	0.844	0.00645	0.0675	0.0197	0.0737	0.0316	0.0147	0.297	0.00154	0.00125
217-6b	0.284	0.00623	0.666	0.00623	0.0384	0.024	0.0117	0.15	0.00146	0.00111
217-7a	0.343	0.00548	0.574	0.00548	0.0717	0.023	0.0107	0.32	0.00152	0.00139
217-7b	0.846	0.00507	0.127	0.0144	0.0131	0.0479	0.0133	0.311	0.00151	0.00139
217-8a	0.496	0.00722	0.439	0.00722	0.0521	0.0325	0.0128	0.382	0.00179	0.00111
217-8b	0.512	0.00703	0.41	0.00703	0.0639	0.0272	0.0139	0.232	0.00173	0.00125
217-1	0.0136	0.00346	0.956	0.00346	0.0271	0.0233	0.00359	1.98	0.00159	0.00111
217-2	0.978	0.00352	0.014	0.0261	0.00614	0.042	0.00194	0.686	0.0016	0.00125
217-3	0.932	0.00355	0.0336	0.00355	0.0292	0.0324	0.00491	0.279	0.00174	0.00125
217-4	0.658	0.00135	0.32	0.00555	0.0174	0.0268	0.00424	0.473	0.00171	0.00111
353-3a	0.554	0.00704	0.36	0.00704	0.0699	0.0305	0.0163	0.344	0.0017	0.00125
353-3b	0.219	0.00268	0.671	0.00695	0.0977	0.0238	0.0119	0.289	0.00157	0.00111
353-4a	0.768	0.00473	0.198	0.00993	0.0283	0.0505	0.00628	0.536	0.00181	0.00125
353-4b	0.684	0.00454	0.224	0.0108	0.0774	0.08	0.0149	0.267	0.00166	0.00111
353-5a	0.767	0.00596	0.159	0.0124	0.0628	0.0303	0.0109	0.357	0.00156	0.00111
353-5b	0.832	0.00619	0.126	0.0111	0.0324	0.035	0.0096	0.397	0.00166	0.00111
353-6a	0.0487	0.00176	0.855	0.006	0.0856	0.0216	0.0105	0.222	0.00199	0.00125
353-6b	0.829	0.00561	0.127	0.00561	0.0373	0.0252	0.00696	0.36	0.00228	0.00111
353-1	0.41	0.000743	0.502	0.00422	0.0811	0.0177	0.0063	0.329	0.00132	0.00097
353-2	0.747	0.00309	0.225	0.00726	0.0252	0.0447	0.00267	0.513	0.00154	0.00097
353-7	0.448	0.0009	0.537	0.0041	0.0122	0.0273	0.00346	0.433	0.00178	0.00125
353-8	0.718	0.00223	0.261	0.00608	0.0165	0.038	0.00408	0.268	0.00177	0.00111
545-1	0.991	0.00293	0.00743	0.026	0.00139	2.6	0	0	0.00216	0.00111
545-2	0.985	0.00277	0.0128	0.024	0.00246	2.8	0	0	0.00187	0.00097
545-4	0.972	0.003	0.0277	0.025	0.000777	2.5	0	0	0.00222	0.00111
857-1	0.974	0.00338	0.0229	0.025	0.00349	2.2	0	0	0.00176	0.00111
857-2	0.84	0.00148	0.158	0.00656	0.00249	3.2	0	0	0.0022	0.00125
857-3	0.36	4.22e-05	0.627	0.0024	0.0111	0.017	0.002	1.9	0.00152	0.00126
857-4	0.278	0.0004	0.719	0.00392	0.00162	0.09	0.00152	0.8	0.00149	0.000558

System (Ken)

List of systematics

Like all experiments, Planck/HFI had a number of "issues" which it needed to track and verify were not compromising the data. While these are discussed in appropriate sections, here we gather them together to give brief summaries of the issues and refer the reader to the appropriate section for more details.

• Cosmic Rays - Unprotected by the atmosphere and more sensitive than previous bolometric experiment, HFI was subjected to many more cosmic ray hits than previous experiments. These were detected, the worst parts of the data flagged as unusable, and "tails" were modeled and removed. This is described in XXXXX
• Elephants - Cosmic rays also hit the 100 mK stage and cause the temperature to vary, inducing small temperature and thus noise variations in the detectors. This is described in XXXXX
• 1.6 K Stage Fluctuations
• 4 K Stage Fluctuations
• Popcorn Noise - Some channels were occasionally affected by what seems to be a "split-level" noise, which has been variously called popcorn noise or random telegraphic signal. These data are usually flagged. This is described in XXXXX
• Jumps - Similar to but distinct from popcorn noise, small jumps were occasionally found in the data streams. These data are usually corrected. This is described in XXXXX.
• 4 K Cooler-Induced EM Noise - The 4 K cooler induced noise in the detectors with very specific frequency signatures, which is filtered. This is described in XXXXX.
• 4 K Cooler-Induced Microphonics - The mechanical cooler was shown in XXXXX to cause very little microphonic parasites in the detector data.
• Pointing-Change Microphonics - The changes in pointing after each pointing period were shown in XXXXX to cause very little microphonic parasitic signal in the detector data.
• Compression - Onboard compression is used to overcome our telemetry bandwidth limitations. This is explained in XXXXX.
• Noise Correlations - Correlations in noise between detectors seems to be negligble but for two polarization sensitive detectors in the same horn. This is discussed in XXXXX.
• Electrical Cross-Talk - Cross-talk is discussed in XXXXX.

• Pointing - The final pointing reconstruction for Planck is near the arcsecond level. This is discussed in XXXXX.
• Focal Plane Geometry - The relative positions of different horns in the focal plane is reconstructed using planets. This is discussed in XXXXX.
• Main Beam - The main beams for HFI are discussed in XXXXX.
• Ruze Envelope - Random imperfections or dust on the mirrors can increase the size of the beam a bit. This is discussed in XXXXX.
• Dimpling - The mirror support structure causes a pattern of small imperfections in the beams, which cause small sidelobe responses outside the main beam. This is discussed in XXXXX.
• Far Sidelobes - Small amounts of light can sometimes hit the detectors from just above the primary or secondary mirrors, or even from reflecting off the baffles. While small, when the Galactic center is in the right position, this can be detected in the highest frequency channels, so this is removed from the data. This is discussed in XXXXX.
• Planet Fluxes - Comparing the known fluxes of planets with the calibration on the CMB dipole is a useful check of calibration. This is done in XXXXX.
• Point Source Fluxes - As with planet fluxes, we also compare fluxes of known, bright point sources with the CMB dipole calibration. This is done in XXXXX.

• Time Constants - The HFI bolometers do not react instantaneously to light; there are small time constants, discussed XXXXX.
• ADC Correction - The HFI Analog-to-Digital Converters are not perfect, and are not used perfectly. Their effects on the calibration are discussed in XXXXX.
• Gain changes with Temperature Changes
• Optical Cross-Talk - This is discussed in XXXXX.
• Bandpass - The transmission curves, or "bandpass" has shown up in a number of places. This is discussed in XXXXX and YYYYY.
• Saturation - While this is mostly an issue only for Jupiter observations, it should be remembered that the HFI detectors cannot observe arbitrarily bright objects. This is discussed in XXXXX.

Summary

(Lamarre) here remind worse sytematics and point to DPC Summary of sucess and limitations. JML. Link to early HFI in flight perf.