Difference between revisions of "CMB spectrum & Likelihood Code"
| Line 9: | Line 9: | ||
<span style="color:red"> UPDATE COMMANDER: Over the multipole range <math> \ell </math> = 2–29, the power spectrum is derived from a component-separation algorithm, ''Commander'': applied to maps in the frequency range 30–353 GHz over 91% of the sky {{PlanckPapers|planck2013-p06}} . The asymmetric error bars associated to this spectrum are the 68% confidence limits and include the uncertainties due to foreground subtraction. </span> | <span style="color:red"> UPDATE COMMANDER: Over the multipole range <math> \ell </math> = 2–29, the power spectrum is derived from a component-separation algorithm, ''Commander'': applied to maps in the frequency range 30–353 GHz over 91% of the sky {{PlanckPapers|planck2013-p06}} . The asymmetric error bars associated to this spectrum are the 68% confidence limits and include the uncertainties due to foreground subtraction. </span> | ||
| − | For multipoles equal or greater than <math>\ell=30</math>, instead, the spectrum is derived from the ''Plik'' likelihood {{PlanckPapers|planck2014-a13}} by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds using the best-fit foreground solution from Planck TT+lowP run | + | For multipoles equal or greater than <math>\ell=30</math>, instead, the spectrum is derived from the ''Plik'' likelihood {{PlanckPapers|planck2014-a13}} by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds using the best-fit foreground solution from Planck TT+lowP LCDM run. Associated 1-sigma errors include beam uncertainties. Both ''Commander'' and ''Plik'' are described in more details in the sections below. |
[[File: Planck2014 TT Dl NORES bin30 w180mm.jpeg|thumb|center|700px|'''CMB TT spectrum. Logarithmic x-scale up to <math>\ell=30</math>, linear at higher <math>\ell</math>; all points with error bars. The red line is the Planck best-fit primordial power spectrum (cf Planck TT+lowP in Table 3 of {{PlanckPapers|planck2014-a15}}). The blue shaded area shows the uncertainties due to cosmic variance alone.''']] | [[File: Planck2014 TT Dl NORES bin30 w180mm.jpeg|thumb|center|700px|'''CMB TT spectrum. Logarithmic x-scale up to <math>\ell=30</math>, linear at higher <math>\ell</math>; all points with error bars. The red line is the Planck best-fit primordial power spectrum (cf Planck TT+lowP in Table 3 of {{PlanckPapers|planck2014-a15}}). The blue shaded area shows the uncertainties due to cosmic variance alone.''']] | ||
| Line 15: | Line 15: | ||
====TE and EE==== | ====TE and EE==== | ||
The Planck best-fit CMB polarization and temperature-polarization cross-correlation power spectra, shown in the figure below, cover the multipole range <math> \ell </math> = 30-1996. The data points relative to the multipole range <math> \ell </math> = 2-29 will be released in a second moment. | The Planck best-fit CMB polarization and temperature-polarization cross-correlation power spectra, shown in the figure below, cover the multipole range <math> \ell </math> = 30-1996. The data points relative to the multipole range <math> \ell </math> = 2-29 will be released in a second moment. | ||
| − | Analogously to the TT case, the <math> \ell\ge 30 </math> spectrum is derived from the ''Plik'' likelihood {{PlanckPapers|planck2014-a13}} by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds using the best-fit foreground solution from Planck TT,TE,EE+lowP run. | + | Analogously to the TT case, the <math> \ell\ge 30 </math> spectrum is derived from the ''Plik'' likelihood {{PlanckPapers|planck2014-a13}} by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds using the best-fit foreground solution from a Planck TT,TE,EE+lowP LCDM run. |
{|style="margin: 0 auto;" | {|style="margin: 0 auto;" | ||
| Line 27: | Line 27: | ||
The <math>\ell \ge 30</math> part of the TT, TE and EE power spectra have been derived by the Plik likelihood, a code that implements a pseudo-Cl based technique, extensively described in Sec. 2 and the Appendix of {{PlanckPapers|planck2013-p08}} and {{PlanckPapers|planck2014-a13}}. Frequency spectra are computed as cross-spectra between half-mission maps. Mask and multipole range choices for each frequency spectrum are summarized in Section 3.3 of {{PlanckPapers|planck2014-a15}} and in {{PlanckPapers|planck2014-a13}}. The final power spectrum is an optimal combination of the 100, 143, 143x217 and 217 GHz spectra, corrected for the best-fit unresolved foregrounds and inter-frequency calibration factors, as derived from the full likelihood analysis (for TT we use the best-fit solutions for the nuisance parameters from the Planck+TT+lowP data combination, while for TE and EE we use the best fit from Planck+TT+lowP, cf Table 3 of {{PlanckPapers|planck2014-a15}}). A thorough description of the models of unresolved foregrounds is given in {{PlanckPapers|planck2014-a13}}. The spectrum covariance matrix accounts for cosmic variance and noise contributions, together with beam uncertainties. The <math>\ell \ge 30</math> CMB TT spectrum and associated covariance matrix are available in two formats: | The <math>\ell \ge 30</math> part of the TT, TE and EE power spectra have been derived by the Plik likelihood, a code that implements a pseudo-Cl based technique, extensively described in Sec. 2 and the Appendix of {{PlanckPapers|planck2013-p08}} and {{PlanckPapers|planck2014-a13}}. Frequency spectra are computed as cross-spectra between half-mission maps. Mask and multipole range choices for each frequency spectrum are summarized in Section 3.3 of {{PlanckPapers|planck2014-a15}} and in {{PlanckPapers|planck2014-a13}}. The final power spectrum is an optimal combination of the 100, 143, 143x217 and 217 GHz spectra, corrected for the best-fit unresolved foregrounds and inter-frequency calibration factors, as derived from the full likelihood analysis (for TT we use the best-fit solutions for the nuisance parameters from the Planck+TT+lowP data combination, while for TE and EE we use the best fit from Planck+TT+lowP, cf Table 3 of {{PlanckPapers|planck2014-a15}}). A thorough description of the models of unresolved foregrounds is given in {{PlanckPapers|planck2014-a13}}. The spectrum covariance matrix accounts for cosmic variance and noise contributions, together with beam uncertainties. The <math>\ell \ge 30</math> CMB TT spectrum and associated covariance matrix are available in two formats: | ||
| − | #Unbinned. TT: 2479 bandpowers (<math>\ell=30-2508</math>); TE or EE:1697 bandpowers (<math>\ell=30-1996</math>). | + | #Unbinned. TT: 2479 bandpowers (<math>\ell=30-2508</math>); TE or EE: 1697 bandpowers (<math>\ell=30-1996</math>). |
#Binned, in bins of <math> \Delta\ell=30 </math>. TT: 83 bandpowers. TE or EE: 66 bandpowers. We bin the <math> C_\ell </math> power spectrum with a weight proportional to <math> \ell (\ell+1) </math>, so that the <math> C_{\ell_b} </math> binned bandpower centered in <math> \ell_b </math> is: <math> \\ C_{\ell_b}=\Sigma_{\ell \in b} w_{\ell_b\ell} C_\ell \quad \text{with} \quad w_{\ell_b\ell}=\frac{\ell (\ell+1)}{\Sigma_{\ell \in b} \ell (\ell+1)}. \\</math> Equivalently, using the matrix formalism, we can construct the binning matrix B as: <math>\\ B_{\ell_b \ell}=w_{\ell_b\ell} \\ </math> where B is a <math> n_b\times n_\ell</math> matrix, with <math>n_b=83</math> the number of bins and <math>n_\ell=2479</math> the number of unbinned multipoles. Thus: <math> \\ \vec{C}_\mathrm{binned}=B \, \vec{C} \\ \mathrm{cov_\mathrm{binned}}= B\, \mathrm{cov}\, B^T \\ \ell_b=B\, \ell \\ </math> Here, <math> \vec{C}_{binned}\, (\vec{C}) </math> is the vector containing all the binned (unbinned) <math>C_\ell</math> bandpowers, <math>\mathrm{cov} </math> is the covariance matrix and <math>\ell_b</math> is the weighted average multipole in each bin. The binned <math>D_{\ell_B}</math> power spectrum is then calculated as: <math> \\ D_{\ell_b}=\frac{\ell_b (\ell_b+1)}{2\pi} C_{\ell_b} </math>. | #Binned, in bins of <math> \Delta\ell=30 </math>. TT: 83 bandpowers. TE or EE: 66 bandpowers. We bin the <math> C_\ell </math> power spectrum with a weight proportional to <math> \ell (\ell+1) </math>, so that the <math> C_{\ell_b} </math> binned bandpower centered in <math> \ell_b </math> is: <math> \\ C_{\ell_b}=\Sigma_{\ell \in b} w_{\ell_b\ell} C_\ell \quad \text{with} \quad w_{\ell_b\ell}=\frac{\ell (\ell+1)}{\Sigma_{\ell \in b} \ell (\ell+1)}. \\</math> Equivalently, using the matrix formalism, we can construct the binning matrix B as: <math>\\ B_{\ell_b \ell}=w_{\ell_b\ell} \\ </math> where B is a <math> n_b\times n_\ell</math> matrix, with <math>n_b=83</math> the number of bins and <math>n_\ell=2479</math> the number of unbinned multipoles. Thus: <math> \\ \vec{C}_\mathrm{binned}=B \, \vec{C} \\ \mathrm{cov_\mathrm{binned}}= B\, \mathrm{cov}\, B^T \\ \ell_b=B\, \ell \\ </math> Here, <math> \vec{C}_{binned}\, (\vec{C}) </math> is the vector containing all the binned (unbinned) <math>C_\ell</math> bandpowers, <math>\mathrm{cov} </math> is the covariance matrix and <math>\ell_b</math> is the weighted average multipole in each bin. The binned <math>D_{\ell_B}</math> power spectrum is then calculated as: <math> \\ D_{\ell_b}=\frac{\ell_b (\ell_b+1)}{2\pi} C_{\ell_b} </math>. | ||
| Line 38: | Line 38: | ||
* compact sources catalog | * compact sources catalog | ||
| − | ; High-l spectrum (<math>30 \ge | + | ; High-l spectrum (<math>30 \ge \ell \lesssim 2500</math>): |
* 100, 143, 143x217 and 217 GHz spectra and their covariance matrix (Sec. 3.3 {{PlanckPapers|planck2014-a15}}) | * 100, 143, 143x217 and 217 GHz spectra and their covariance matrix (Sec. 3.3 {{PlanckPapers|planck2014-a15}}) | ||
| Line 55: | Line 55: | ||
: with the low ell part of the spectrum, not binned, and for l=2-49. The table columns are | : with the low ell part of the spectrum, not binned, and for l=2-49. The table columns are | ||
# ''ELL'' (integer): multipole number | # ''ELL'' (integer): multipole number | ||
| − | # ''D_ELL'' (float): <math>D_l</math> as described | + | # ''D_ELL'' (float): <math>D_l</math> as described above |
# ''ERRUP'' (float): the upward uncertainty | # ''ERRUP'' (float): the upward uncertainty | ||
# ''ERRDOWN'' (float): the downward uncertainty | # ''ERRDOWN'' (float): the downward uncertainty | ||
| Line 64: | Line 64: | ||
# ''L_MIN'' (integer): lowest multipole of bin | # ''L_MIN'' (integer): lowest multipole of bin | ||
# ''L_MAX'' (integer): highest multipole of bin | # ''L_MAX'' (integer): highest multipole of bin | ||
| − | # ''D_ELL'' (float): <math> | + | # ''D_ELL'' (float): <math>D_\ell<\math> as described above |
# ''ERR'' (float): the uncertainty | # ''ERR'' (float): the uncertainty | ||
| − | |||
| − | |||
| − | |||
; UNBINNED HIGH-ELL (BINTABLE) | ; UNBINNED HIGH-ELL (BINTABLE) | ||
: with the high-ell part of the spectrum, unbinned, in 2979 bins covering <math>\langle l \rangle = 30-2508\ </math>. The table columns are as follows: | : with the high-ell part of the spectrum, unbinned, in 2979 bins covering <math>\langle l \rangle = 30-2508\ </math>. The table columns are as follows: | ||
# ''ELL'' (integer): multipole | # ''ELL'' (integer): multipole | ||
| − | # ''D_ELL'' (float): $D_l$ as described | + | # ''D_ELL'' (float): $D_l$ as described above |
# ''ERR'' (float): the uncertainty | # ''ERR'' (float): the uncertainty | ||
| − | |||
| − | |||
| − | The spectra give | + | The spectra give <math>D_\ell = \ell(\ell+1)C_\ell / 2\pi </math> in units of <math>\mu\, K^2</math>. |
| + | <!-- | ||
The CMB spectrum is also given in a simple text comma-separated file: | The CMB spectrum is also given in a simple text comma-separated file: | ||
* ''{{PLASingleFile | fileType=cosmo | name=COM_PowerSpect_CMB_R1.10.txt |link=COM_PowerSpect_CMB_R1.10.txt}}'' | * ''{{PLASingleFile | fileType=cosmo | name=COM_PowerSpect_CMB_R1.10.txt |link=COM_PowerSpect_CMB_R1.10.txt}}'' | ||
| + | --> | ||
==Likelihood== | ==Likelihood== | ||
The likelihood will soon be released with an accompanying paper and an Explanatory Supplement update. | The likelihood will soon be released with an accompanying paper and an Explanatory Supplement update. | ||
Revision as of 17:07, 4 February 2015
Contents
CMB spectra[edit]
General description[edit]
TT[edit]
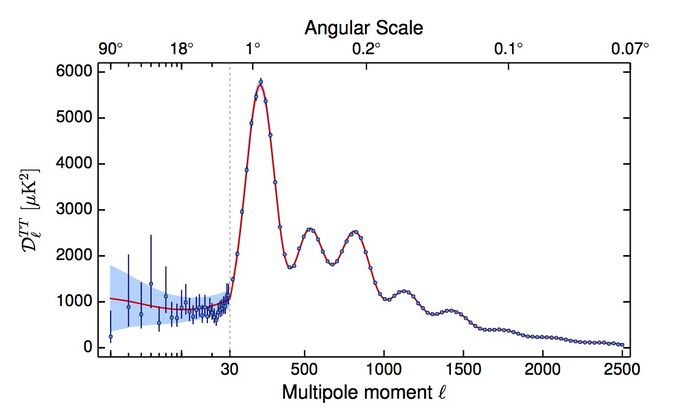
The Planck best-fit CMB temperature power spectrum, shown in figure below, covers the wide range of multipoles = 2-2508. UPDATE COMMANDER: Over the multipole range = 2–29, the power spectrum is derived from a component-separation algorithm, Commander: applied to maps in the frequency range 30–353 GHz over 91% of the sky Planck-2013-XII[1] . The asymmetric error bars associated to this spectrum are the 68% confidence limits and include the uncertainties due to foreground subtraction.
For multipoles equal or greater than , instead, the spectrum is derived from the Plik likelihood Planck-2015-A11[2] by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds using the best-fit foreground solution from Planck TT+lowP LCDM run. Associated 1-sigma errors include beam uncertainties. Both Commander and Plik are described in more details in the sections below.
TE and EE[edit]
The Planck best-fit CMB polarization and temperature-polarization cross-correlation power spectra, shown in the figure below, cover the multipole range = 30-1996. The data points relative to the multipole range = 2-29 will be released in a second moment. Analogously to the TT case, the spectrum is derived from the Plik likelihood Planck-2015-A11[2] by optimally combining the spectra in the frequency range 100-217 GHz, and correcting them for unresolved foregrounds using the best-fit foreground solution from a Planck TT,TE,EE+lowP LCDM run.
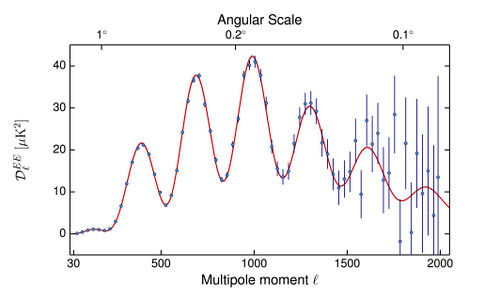 CMB EE spectrum. The red line is the Planck best-fit primordial power spectrum (cf Planck TT+lowP in Table 3 of Planck-2015-A13[3]). The blue shaded area shows the uncertainties due to cosmic variance alone. |
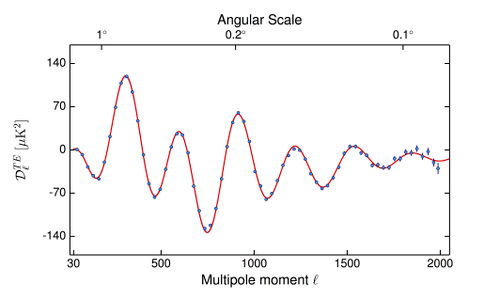 CMB TE spectrum. The red line is the Planck best-fit primordial power spectrum (cf Planck TT+lowP in Table 3 of Planck-2015-A13[3]). The blue shaded area shows the uncertainties due to cosmic variance alone. |
Production process[edit]
UPDATE COMMANDER The < 50 part of the Planck TT power spectrum is derived from the Commander approach, which implements Bayesian component separation in pixel space, fitting a parametric model to the data by sampling the posterior distribution for the model parameters Planck-2013-XII[1]. The power spectrum at any multipole is given as the maximum probability point for the posterior distribution, marginalized over the other multipoles, and the error bars are 68% confidence level Planck-2013-XV[4].
The part of the TT, TE and EE power spectra have been derived by the Plik likelihood, a code that implements a pseudo-Cl based technique, extensively described in Sec. 2 and the Appendix of Planck-2013-XV[4] and Planck-2015-A11[2]. Frequency spectra are computed as cross-spectra between half-mission maps. Mask and multipole range choices for each frequency spectrum are summarized in Section 3.3 of Planck-2015-A13[3] and in Planck-2015-A11[2]. The final power spectrum is an optimal combination of the 100, 143, 143x217 and 217 GHz spectra, corrected for the best-fit unresolved foregrounds and inter-frequency calibration factors, as derived from the full likelihood analysis (for TT we use the best-fit solutions for the nuisance parameters from the Planck+TT+lowP data combination, while for TE and EE we use the best fit from Planck+TT+lowP, cf Table 3 of Planck-2015-A13[3]). A thorough description of the models of unresolved foregrounds is given in Planck-2015-A11[2]. The spectrum covariance matrix accounts for cosmic variance and noise contributions, together with beam uncertainties. The CMB TT spectrum and associated covariance matrix are available in two formats:
- Unbinned. TT: 2479 bandpowers (); TE or EE: 1697 bandpowers ().
- Binned, in bins of . TT: 83 bandpowers. TE or EE: 66 bandpowers. We bin the power spectrum with a weight proportional to , so that the binned bandpower centered in is: Equivalently, using the matrix formalism, we can construct the binning matrix B as: where B is a matrix, with the number of bins and the number of unbinned multipoles. Thus: Here, is the vector containing all the binned (unbinned) bandpowers, is the covariance matrix and is the weighted average multipole in each bin. The binned power spectrum is then calculated as: .
Inputs[edit]
UPDATE COMMANDER
- Low-l spectrum ()
- frequency maps from 30–353 GHz
- common mask Planck-2013-XII[1]
- compact sources catalog
- High-l spectrum ()
- 100, 143, 143x217 and 217 GHz spectra and their covariance matrix (Sec. 3.3 Planck-2015-A13[3])
- best-fit foreground templates and inter-frequency calibration factors (Table 3 of Planck-2015-A13[3])
- Beam transfer function uncertainties Planck-2015-A07[5]
File names and Meta data[edit]
CHECK EXTENSION NAMES
The CMB spectrum and its covariance matrix are distributed in a single FITS file named
- COM_PowerSpect_CMB_R2.nn.fits
which contains 5 extensions
- LOW-ELL (BINTABLE)
- with the low ell part of the spectrum, not binned, and for l=2-49. The table columns are
- ELL (integer): multipole number
- D_ELL (float): as described above
- ERRUP (float): the upward uncertainty
- ERRDOWN (float): the downward uncertainty
- BINNED HIGH-ELL (BINTABLE)
- with the high-ell part of the spectrum, binned into 83 bins covering in bins of width (with the exception of the last bin that is smaller). The table columns are as follows:
- ELL (integer): mean multipole number of bin
- L_MIN (integer): lowest multipole of bin
- L_MAX (integer): highest multipole of bin
- D_ELL (float): . The table columns are as follows:
- ELL (integer): multipole
- D_ELL (float): $D_l$ as described above
- ERR (float): the uncertainty
The spectra give in units of .
Likelihood[edit]
The likelihood will soon be released with an accompanying paper and an Explanatory Supplement update.
References[edit]
- ↑ 1.01.11.2 Planck 2013 results. XI. Component separation, Planck Collaboration, 2014, A&A, 571, A11
- ↑ 2.02.12.22.32.4 Planck 2015 results. XI. CMB power spectra, likelihoods, and robustness of cosmological parameters, Planck Collaboration, 2016, A&A, 594, A11.
- ↑ 3.03.13.23.33.43.53.6 Planck 2015 results. XIII. Cosmological parameters, Planck Collaboration, 2016, A&A, 594, A13.
- ↑ 4.04.1 Planck 2013 results. XV. CMB power spectra and likelihood, Planck Collaboration, 2014, A&A, 571, A15
- ↑ Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
Cosmic Microwave background
Flexible Image Transfer Specification