Difference between revisions of "LFI design, qualification, and performance"
(→Photometric Calibration) |
(→Radiometer Chain Assembly (RCA)) |
||
| Line 70: | Line 70: | ||
</math> | </math> | ||
| − | where <math><V_{\rm sky}> \;</math> and <math><V_{\rm ref}> \;</math> are the average sky and reference voltages calculated in a defined time range. | + | where <math>< V_{\rm sky}> \;</math> and <math>< V_{\rm ref}> \;</math> are the average sky and reference voltages calculated in a defined time range. |
The white noise spectral density at the output of each diode is essentially independent from the reference-load absolute temperature and is given by: | The white noise spectral density at the output of each diode is essentially independent from the reference-load absolute temperature and is given by: | ||
Revision as of 09:30, 15 December 2014
Contents
- 1 Instrument description
- 2 Ground Tests
- 3 In-flight Calibration
- 4 Performance Summary
- 5 Systematic Effects
- 6 The Sorption Cooler
- 7 References
Instrument description[edit]
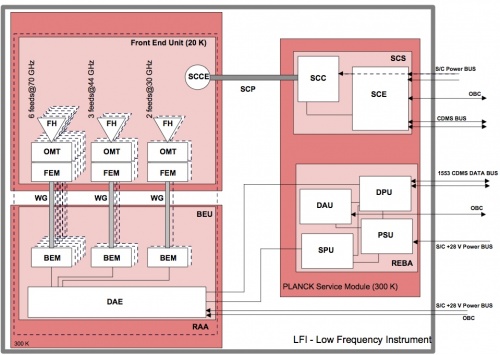
The LFI instrument (see Fig. 1 in the LFI overview) consists of a 20 K focal plane unit hosting the corrugated feed horns, the orthomode transducers (OMTs) and the receiver front-end modules (FEMs). Forty four composite waveguides [1] are interfaced with three conical thermal shields and connect the front-end modules to the warm (~300 K) back-end unit (BEU) containing a further radio frequency amplification stage, detector diodes and all the electronics for data acquisition and bias supply.
Best LFI noise performance is obtained with receivers based on InP High Electron Mobility Transistor (HEMT) low noise amplifiers (LNAs) for minimal power dissipation and best performance. To further minimise power consumption in the focal plane, the radiometers are split into two sub-assemblies connected by waveguides, one located at the telescope focal area, the other on the 300 K portion of the Planck satellite. These design features allow the entire front-end LNAs dissipation to be <0.55 W, which enables the active cooling of the focal assembly. This is achieved with a vibration-less hydrogen sorption cooler, which also provides 18 K pre-cooling to the HFI helium J-T cooler. Two sorption cooler units are included in the flight hardware.
As shown schematically in Fig. 1 below, the LFI consists of the following subsystems:
- Radiometer Array Assembly (RAA)
- Sorption Cooler Subsystem (SCS)
- Radiometer Electronics Box Assembly (REBA)
The RAA includes the Front End Unit (FEU) and the Back End Unit (BEU), connected via waveguides. The FEU is located at the focus of the telescope, as one component of the joint LFI/HFI focal assembly (see sections below). The BEU is mounted on the top of the Planck service module (SVM). The REBA (Radiometer Electronics Box Assembly) and the warm parts of the Sorption Cooler System (SCS) are located on one of the lateral panels of the SVM. The FEU and the Sorption Cooler Compressor (SCC) are connected by concentric stainless steel tubes. The smaller tube carries hydrogen at ∼60 atmospheres from the cooler compressors to the FEU, while the larger tube returns the hydrogen at ∼0.3 atmospheres. These units are described in following sections and in the Annexes, the SCS is described in details in the Sorption Cooler section. All LFI units are linked together by the LFI harness, which also connects to the spacecraft interface.
Radiometer Array Assembly (RAA)[edit]
The Radiometer Array Assembly (RAA) consists of two main units (the front end unit, FPU and the Back End Unit, BEU), connected by a set of waveguides. The Focal Plane Unit (FPU) is the heart of the LFI instrument and it contains the feed array and associated orthomode transducers (OMTs) and FEMs, all cooled to 20 K by the sorption cooler. The FPU comprises a set of 11 modules, which are mounted on a mechanical support which meets the thermo-mechanical requirements of the instrument and adds thermal inertia. The BEU comprises the radiometer Back End Modules (BEM) and the Data Acquisition Electronics (DAE), which are connected by an internal harness. The HFI Unit is located inside the LFI FPU and supported by the LFI structure. The LFI structure gives the mechanical and thermal interface to the HFI unit with the proper stiffness and thermal de-coupling. The LFI structure also guarantees the proper alignment of the HFI detector with the telescope focal plane.
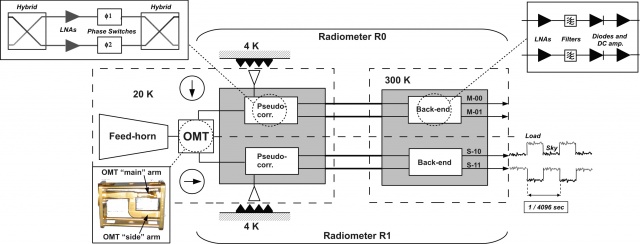
The time scale of the stability of the receiver is driven by the 1 rpm rotation speed of the spacecraft, which requires a very low 1/f-noise or gain variation of the low noise amplifiers and other components. The LFI uses a pseudo-correlation receiver concept (Fig. 2 below). This radiometer concept is chosen to maximise the stability of the instrument by reducing the effect of non-white noise generated in the radiometer itself. In this scheme, the difference between the inputs to each of the chains (the signal from the telescope and that from a reference black body respectively) is continuously being observed. To remove the effect of instability in the back-end amplifiers and detector diodes, it is necessary to switch the signal detected at the diodes at high rate. The signals from the sky and from a reference load are combined by a hybrid coupler, amplified in two independent amplifier chains, and separated out by another hybrid. The sky and the reference load power can then be measured and differenced. Since the reference signal has been subject to the same gain variations in the two amplifier chains as the sky signal, the true sky power can be recovered. The differencing receiver greatly improves the stability if the two input signals are almost equal, at a cost of a factor of in sensitivity compared to a perfectly stable total-power radiometer with the same noise temperature and bandwidth. This radiometer concept is capable of greatly reducing the knee frequency. We define as Radiometer Chain Assembly (RCA, see Fig. 2) each functional unit from the feed horn to the BEM. The RAA therefore includes a set of 11 RCAs and the Data Acquisition Electronics (see also Fig. 1 above), all mounted on a suitable mechanical structure. Although there are differences in the details of the radiometer chains at different frequencies, their overall configuration is similar, and a general description of its design is provided in this section. Planck LFI has 11 Radiometer Chain Assembly (RCA). Each RCA is constituted by feed horn and FEM in the FEU (at 20 K), BEM (at 300 K) in the BEU and four waveguides that connect each FEM-BEM couple. The frequency distribution of the RCA is the following:
- 2 RCAs at 30 GHz;
- 3 RCAs at 44 GHz;
- 6 RCAs at 70 GHz.
Radiometer Chain Assembly (RCA)[edit]
Every RCA consists of two radiometers, each feeding two diode detectors (see Fig. 2 above), for a total of 44 detectors. The 11 RCAs are labelled by a numbers from 18 to 28 as outlined in Fig. 1 in LFI overview, right panel.
Fig. 2 provides a more detailed description of each radiometric receiver. In each RCA, the two perpendicular linear polarisation components split by the OMT propagate through two independent pseudo-correlation differential radiometers, labelled as M or S depending on the arm of the OMT they are connected to (Main or Side, see lower-left inset of Fig. 2).
In each radiometer the sky signal coming from the OMT output is continuously compared with a stable 4 K blackbody reference load mounted on the external shield of the HFI 4 K box [2]. After being summed by a first hybrid coupler, the two signals are amplified by ~30 dB, see upper-left inset of Fig. 2. The amplifiers were selected for best operation at low drain voltages and for gain and phase match between paired radiometer legs, which is crucial for good balance. Each amplifier is labelled with codes 1, 2 so that the four outputs of the LNAs can be named with the sequence: M1, M2 (radiometer M) and S1, S2 (radiometer S). Tight mass and power constraints called for a simple design of the Data Acquisition Electronics (DAE) box so that power bias lines were divided into five common-grounded power groups with no bias voltage readouts; only the total drain current flowing through the front-end amplifiers is measured and is available to the house-keeping telemetry (this design has important implications for front-end bias tuning, which depends critically on the satellite electrical and thermal configuration and was repeated at all integration stages, during on-ground and in-flight satellite tests). A phase shift (or phase switch) alternating between and at the frequency of 4096 Hz is applied in one of the two amplification chains and then a second hybrid coupler separates back the sky and reference load components that are further amplified and detected in the warm BEU, with a voltage output ranging from -2.5 V to +2.5 V.
Each radiometer has two output diodes which are labelled with binary codes 00, 01 (radiometer M) and 10, 11 (radiometer S), so that the four outputs of each radiometric chain can be named with the sequence: M-00, M-01, S-10, S-11.
After detection, an analog circuit in the DAE box removes a programmable offset in order to obtain a nearly null DC output voltage and a programmable gain is applied to increase the signal dynamics and optimally exploit the ADC input range. After the ADC, data are digitally down-sampled, re-quantised and compressed in the REBA according to a scheme described in [3][4], before preparing telemetry packets. On ground, telemetry packets are converted to sky and reference load time ordered data after calibrating the ADU samples into volt considering the applied offset and gain factors.
To first order, the mean differential power output for each of the four receiver diodes can be written as follows [5][6]Planck-PreLaunch-II[7]:
where is the total gain, is the Boltzmann constant, the receiver bandwidth and is the diode constant. and are the average sky and reference load antenna temperatures at the inputs of the first hybrid and is the receiver noise temperature.
The gain modulation factor [6]Planck-Early-V[8], , is defined by:
and is used to balance (in software) the temperature offset between the sky and reference load signals and minimise the residual 1/ noise in the differential datastream. This parameter is calculated from the average uncalibrated total power data using the relationship:
where and are the average sky and reference voltages calculated in a defined time range. The white noise spectral density at the output of each diode is essentially independent from the reference-load absolute temperature and is given by:
If the front-end components are not perfectly balanced, then the separation of the sky and reference load signals after the second hybrid is not perfect and the outputs are mixed. First-order deviations in white noise sensitivity from the ideal behaviour are caused mainly by noise temperature and phase-switch amplitude mismatches. Following the notation used in [5], we define , the imbalance in front end noise temperature, and and , the imbalance in signal attenuation in the two states of the phase switch. Equation above for the two diodes of a slightly imbalanced radiometer then becomes
which is identical for the two diodes apart from the sign of the term , representing the phase switch amplitude imbalance. This indicates that the isolation loss caused by this imbalance generates an anti-correlation between the white noise levels of the single-diode data streams. For this reason, the LFI scientific data streams are obtained by averaging the voltage outputs from the two diodes in each radiometer:
where and are inverse-variance weights calculated from the data as discussed in Planck-Early-V[8]. This way, the diode-diode anti-correlation is cancelled, and the radiometer white noise becomes
In Equations above, , while is a term given by:
See Diode Combination section for the details of the diode combination procedure.
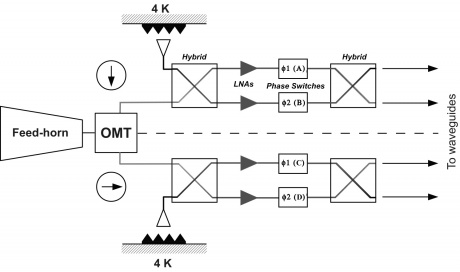
In Fig. 3 below we show a close-up of the two front end modules of an RCA with the four phase switches which are labelled with the four letters A and B (main arm), C and D (side arm). Each phase switch is characterised by two states: state 0 (no phase shift applied to the incoming wave) and state 1 ( phase shift applied) and can either stay fixed in a state or switch at 4 kHz between the two states.
Phase switches are clocked and biased by the DAE and their configuration can be programmed via telecommand. In order to simplify the instrument electronics, phase switches are configured and operated in pairs: A/C and B/D. This means that if phase switches A and C are switching at 4 kHz then B and D are fixed both in the same state (either 0 or 1). This simplification, required during the design phase to comply with mass and power budgets, comes at the price of loosing some setup redundancy.
Feed Horns (FH)[edit]
Dual profiled corrugated horns have been selected at all LFI frequencies as the best design in terms of shape of the main lobe, level of the side lobes, control of the phase centre, and compactness. Details of the design, flight model and tests of Planck-LFI feed horns can be found in [9] and in the corresponding Annex section.
OrthoMode Transducers (OMT)[edit]
The Ortho–Mode Transducer (OMTs) separates the radiation collected by the feed horn in two orthogonal polarisation components. It consists of a circular to square waveguide transition (directly connected to the FH), a square waveguide section and two separate rectangular waveguide (the through and side arms, which separate and pick up the orthogonal polarisation, connected with the FEU). On the side arms is always present a 90 degrees bend, while a twist is also necessary on the main (30 and 44 GHz) and side (70 GHz) arm, in order to math the FEU polarisation.
The details of the flight models and measurements of the Planck LFI ortho-mode transducers can be found in [10] and in the corresponding Annex section.
Front End Modules (FEM)[edit]
Front End Modules are located in the FPU, just in cascade of the Feed Horn and the Ortho Mode Transducers. 70 GHz FEMs are mounted onto the inner wall of the mainframe (the wall facing HFI instrument) from the HFI side. 44 and 30 GHz FEMs are inserted into the mainframe from the WG side and fixed to the bottom plate. Screws to bottom plate are inserted from WG side. The LFI FEMs are the first active stage of amplification of the radiometer chain. Each FEM contains four amplification paths. Each path is composed by several cascaded LNAs followed by a phase switch. Two passive hybrids, at the input and output of the FEM, are used to mix couples of signals of the same radiometer (see Fig. 3). This makes the instabilities of each chain to be applied to both the sky and load signals.
The passive hybrid coupler (magic-tee) combines the signals from the sky and cold load with a fixed phase offset of either 90 deg or 180 deg between them. It has a 20% bandwidth, low loss, and amplitude balance needed at the output to ensure adequate signal isolation.
The details of the design, development and verification of the 70 GHz front-end modules for the Planck Low Frequency Instrument can be found in [11] and in the corresponding Annex section.
Waveguides[edit]
The LFI Front End Unit (FEU) is connected to the Back End Unit (BEU) by 44 rectangular waveguides approximately 1.5-2.0 meter long. Each waveguide exhibits low voltage standing wave ratio, low thermal conductivity, low insertion loss, and low mass. In addition, the waveguide path shall permit the LFI/HFI integration and the electrical bonding between FPU and BEU. Because of the Focal Plane Unit arrangement, the waveguides are in general twisted and bended in different planes and with different angles, depending on the particular waveguide. From the thermal point of view the waveguides have to connect 2 systems (BEM and FEM) that are at very different temperatures. At BEM level the waveguides are at a temperature of 300K while at FEM level the temperature is 20K. The waveguides have to reduce the thermal flow from 300K to 20K. In Fig. 1 in LFI overview (left panel) a conceptual sketch of the LFI configuration is shown.
Details of the Planck-LFI flight model of the composite waveguides can be found in [1] and in the corresponding Annex section.
Back End Modules (BEM)[edit]
The BEMs are composed by four identical channels each made of Low Noise Amplifiers (LNA), RF Band Pass Filter, RF to DC diode detector and DC amplifiers. The FEM output signals are connected by waveguide from the Focal Plane Unit (FPU) assembly to the Back End Modules (BEM’s) housed adjacent to the Data Acquisition Electronics (DAE) assembly. To maintain compatibility with the FEM’s, each BEM accommodates four receiver channels from the four waveguide outputs of each FEM. The BEM internal signal routes are not cross coupled and can be regarded as four identical parallel circuits. Each BEM is constructed as two mirror halves. The two amplifier/detector assemblies each contain two amplifier/detector circuits. Each is supplied from one of a pair of printed circuit boards which also house two DC output amplifiers.
The details of the design, development and verification of the 30 and 44 GHz back-end modules for the Planck Low Frequency Instrument can be found in [12]. The details of the design, development and verification of the 70 GHz back-end modules for the Planck Low Frequency Instrument can be found in [11]. Details are reported also in the corresponding Annex section.
4K Load[edit]
The purpose of the 4 K reference load is to provide the radiometer with a stable reference signal. Reducing the input offset (the radiometric temperature difference between the sky and the reference load) reduces the minimum achievable radiometer 1/f noise knee frequency for a given amplifier fluctuation spectrum. A reference load temperature that matches the sky temperature (approximately 2.7 K) would be ideal.
Details of the design, characteristics and performance of the LFI 4K reference load units are given in [2] and in the corresponding section of the Annexes.
Naming Convention[edit]
The naming of all the LFI elements is described in the previous sections but here is summarized again for clarity.
The 11 RCAs are labelled by a numbers from 18 to 28 as outlined in Fig. 1 in LFI overview, right panel. In each RCA, the two perpendicular linear polarisation components are labelled as M or S according to the arm of the OMT they are connected to (Main or Side, see lower-left inset of Fig. 2).
Each front-end amplifier (see upper-left inset of Fig. 2) is labelled with codes 1, 2 so that the four outputs of the FEM LNAs can be named with the sequence: M1, M2 (radiometer M) and S1, S2 (radiometer S).
Each radiometer has two output diodes (see upper-right inset of Fig. 2) which are labelled with binary codes 00, 01 (radiometer M) and 10, 11 (radiometer S), so that the four outputs of each radiometric chain can be named with the sequence: M-00, M-01, S-10, S-11.
REBA[edit]
The Radiometer Electronics Box Assembly (REBA) is the electronic box in charge of processing the digitized scientific data and to manage the overall instrument. It is also in charge of the communication with the spacecraft. There are two REBA boxes, one nominal and one redundant. The redundancy concept is cold, which means that both boxes are never ON at the same time; the operation of each unit shall be managed by the spacecraft switching-on the corresponding unit. The REBA ASW (Application SoftWare) is the same in each REBA box.
A detailed description of the Planck LFI REBA can be found in [3] and in the corresponding section of the Annexes.
Instrument On-board Software[edit]
The REBA software is the on board software of LFI. It is installed in the two computing subunits of REBA: the DPU (Digital Processing Unit), responsible of the control and monitoring of the instrument and the interface with the spacecraft and; the SPU (Signal Processing Unit), responsible of the data reduction and compression.
Details can be found in the corresponding section of the Annexes.
Reduction and Compression of Science Data[edit]
To asses stability against 1/f noise, the Low Frequency Instrument (LFI) on-board the Planck mission will acquire data at a rate much higher than the data rate allowed by the science telemetry bandwidth of 35.5 kbps. The data are processed by an on-board pipeline, followed on-ground by a decoding and reconstruction step, to reduce the volume of data to a level compatible with the bandwidth while minimizing the loss of information. The on-board processing of the scientific data used by Planck/LFI to fit the allowed data-rate is an intrinsically lossy process which distorts the signal in a manner which depends on a set of five free parameters () for each of the 44 LFI detectors. A brief description of the characteristics of this algorithm and the level of distortion introduced by the on-board processing as a function of these parameters can be found in the corresponding section of the Annexes, a full description of the Planck LFI on-board data handling system and the tuning and optimization method of the on-board processing chain in [4].
The strategy adopted to fit into the bandwidth relies on three on-board processing steps: downsampling, pre-processing the data to ensure loss-less compression, and loss-less compression itself. To demonstrate these steps, a model of the input signal shall be used. It has to be noted that while the compression is loss-less, the pre-processing is not, due to the need to rescale the data and convert them in integers, (a process named data re-quantization). However, the whole strategy is designed to asses a strict control of the way in which lossy operations are done, of the amount of information loss in order to asses optimal compression rate with minimal information loss.
Instrument Operations[edit]
Operational Modes[edit]
The operations of the LFI are designed to be automatic and require little if any intervention from the ground. A small amount of commands is required for operating the instrument and eventually for diagnostic and reconfiguration purposes. Each sky survey is conducted by the LFI with the instrument in the Normal Operations Mode mode. No deployable elements, or mechanically moving parts are included in the instrument. The scanning of the sky is achieved by progressive repointing of the satellite spin axis, with the Sun direction always within a cone 10 degrees from the spin axis. Within the Normal Science Mode the instrument can be configured in order to fit with different science or diagnostic needs without changing the power consumption and thus the temperature in the FPU. Changes in power consumption in the FPU are minimised and should occur only in the case that failures in the radiometers that could create interference problems require an RCA to be switched off. Power adjustments on the first stage of the HEMT amplifiers which are contemplated, require extremely small power level variations.
A brief summary of the LFI Operational Modes and the transitions between them is given in the corresponding section of the Annexes.
Ground Tests[edit]
During its development, the LFI flight model was calibrated and tested at various integration levels from sub-systems [13] to individual integrated receivers Planck-PreLaunch-XIII[14] and the whole receiver array Planck-PreLaunch-VII[15]. In every campaign we performed tests according to the following classification:
- Functionality tests, performed to verify the instrument functionality.
- Tuning tests, to tune radiometer parameters (biases, DC electronics gain and offset, digital quantisation and compression) for optimal performance in flight-like thermal conditions.
- Basic calibration and noise performance tests, to characterise instrument performance (photometric calibration, isolation, linearity, noise and stability) in tuned conditions.
- Susceptibility tests, to characterise instrument susceptibility to thermal and electrical variations.
Where possible, the same tests were repeated in several test campaigns, in order to ensure enough redundancy and confidence in the instrument behaviour repeatability. A matrix showing the instrument parameters measured in the various test campaigns is provided in Table 1 of Planck-PreLaunch-VII[15].
The ground test campaign was developed in three main phases: cryogenic tests on the individual RCAs, cryogenic tests on the integrated receiver array (the so-called radiometer array assembly, RAA) and system-level tests after the integration of the LFI and HFI instruments onto the satellite. The first two phases were carried out at the Thales Alenia Space - Italia laboratories located in Vimodrone (Milano, Italy) (note that receiver tests on 70 GHz RCAs were carried out in Finlad, at Yilinen laboratories), system level tests (SLT) were conducted in a dedicated cryofacility at the Centre Spatiale de Liege (CSL) located in Liege (Belgium).
In Table 1 below we list the temperature of the main cold thermal stages during ground tests compared to in-flight nominal values. These values show that system-level tests were conducted in conditions that were as much as possible flight-representative, while results obtained during RCA and RAA tests needed to be extrapolated to flight conditions to allow comparison. Details about the RCA test campaign are discussed in Planck-PreLaunch-XIII[14] while the RAA tests and the extrapolation methods are presented in Planck-PreLaunch-VII[15].
| Temperature | Nominal | RCA tests | RAA tests | System-level |
|---|---|---|---|---|
| Sky | ~ 3 K | ≳ 8 K | ≳ 18.5 K | ~ 4 K |
| Ref. load | ~ 4.5 K | ≳ 8 K | ≳ 18.5 K | ~ 4.5 K |
| Front-end unit | ~ 20 K | ~ 20 K | ~ 26 K | ~ 20 K |
During the various test campaigns the instrument was switched off and moved several times in a time period of about three years. A series of functional tests were always repeated at each location and also in flight, in order to verify the instrument functionality and the response repeatability. No failures or major problems have been identified due to transport and integration procedures.
The expected Planck LFI scientific performance, resulting mainly from cryogenic system level tests, are described in Planck-PreLaunch-VII[15] .
In-flight Calibration[edit]
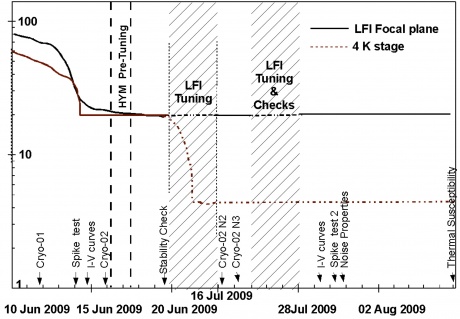
The LFI Commissioning and Calibration and Performance Verification (CPV) phases started on June, 2009 and lasted until August, when Planck started scanning the sky in nominal mode. At the onset of CPV, the active cooling started when the radiating surfaces on the payload module reached their working temperatures (~50 K on the V-groove, and ~40 K on the reflectors) by passive cooling. This was achieved during the transfer phase. Nominal temperatures were achieved on July, 2009, when the dilution cooler temperature reached 0.1 K Planck-Early-II[16][17]. The cooldown of the HFI 4K stage (see Fig. 4 below), was key during CPV for the LFI as it provided a variable input signal that was exploited during bias tuning.
The LFI Commissioning and CPV was carried out in four phases:
- LFI switch on and basic functionality verification (Commissioning),
- Tuning of front-end biases and back-end electronics (CPV),
- Preliminary calibration tests (CPV),
- Thermal tests (CPV).
Details of the LFI Commissioning and CPV test campaign are given in [18].
Performance Summary[edit]
Instrument Scientific Performance[edit]
Optical Parameters[edit]
The most accurate measurements of the LFI main beams have been made with Jupiter, the most powerful unresolved (to Planck) celestial source in the LFI frequency range. Since the LFI feed horns point to different positions on the sky, they detect the signal at different times. To map the beam, each sample in the selected timelines was projected in the -plane perpendicular to the nominal line-of-sight (LOS) of the telescope (and at 85◦ to the satellite spin axis). The and coordinates are defined in terms of the usual spherical coordinates :
To increase the signal-to-noise ratio, data were binned in an angular region of 2′ for the 70 GHz channels and 4′ for the 30 and 44 GHz channels. We recovered all beams down to −20 dB from the peak. An elliptical Gaussian was fit to each beam for both M and S radiometers. Differences between the M and S beams caused by optics and receiver non-idealities are inevitable at some level, but they appear to be well within the statistical uncertainties, and for the purposes of point-source extraction, the beams may be considered identical. For the details of the typical FWHM and ellipticity averaged over each frequency channel, refer to Planck-Early-III[19]. Exhaustive details on all LFI beam parameters are presented in the LFI data processing section - Beams.
Photometric Calibration[edit]
Photometric calibration, i.e., conversion from voltage to antenna temperature, is performed for each radiometer after total power data have been cleaned of 1 Hz frequency spikes (see the LFI data processing section - Spikes Removal section and Planck-Early-V[8], and differenced. Here we report a brief overview of the photometric calibration, for the details see the LFI data processing section - Photometric Calibration.
Our calibrator is the well-known dipole signal induced by Earth and spacecraft motions with respect to the CMB rest frame. The largest calibration uncertainty comes from the presence of the Galaxy and of the CMB anisotropies in the measured signal. We therefore use an iterative calibration procedure in which the dipole is fitted and subtracted, producing a sky map that is then removed from the original data to enhance the dipole signal for the next iteration. Typically, convergence is obtained after a few tens of iterations.
In our current calibration model we use as calibration signal the sum of the solar dipole and the orbital dipole , which is the contribution from Planck’s orbital velocity around the Sun,
where is the angle between the spacecraft axis and the overall dipole axis (solar + orbital). In this equation, the absolute calibration uncertainty is dominated by the uncertainty in = 3.355 mK ± 0.008 mK [20], which is known to about 0.2%. The modulation of the orbital dipole by the Earth motion around the Sun is known with an uncertainty almost three orders of magnitude smaller; however, at least one complete Planck orbit is needed for its measurement. The accuracy of our current calibration can be estimated by taking into account two components: 1) the statistical uncertainty in the regions of weak dipole; and 2) the systematic uncertainty caused by neglecting gain fluctuations that occur on periods shorter than the smoothing window. In our calibration procedure the gain is estimated for every pointing period: if we call the gain estimate from the pointing period we have that the associated uncertainty is
where is the overall number of pointing and is the average of the gains. We then approximate the effect of the smoothing filter as an average over consecutive pointings, so that the overall uncertainty can be estimated as:
Noise Properties[edit]
The noise characteristics of the LFI datastreams are closely reproduced by a simple (white + ) noise model,
where is the power spectrum and . In this model, noise properties are characterised by three parameters, the white noise limit , the knee frequency , and the exponent of the component , also referred to as slope. Here we give noise performance estimates based on one year of operations, details of the analysis are given in LFI data processing section - Noise estimation and in Planck-Early-V[8]Planck-Early-III[19].
Noise properties have been calculated following two different and complementary approaches: 1) fitting equation above to time-ordered data for each radiometer; and 2) building normalised noise maps by differencing data from the first half of the pointing period with data from the second half of the pointing period to remove the sky signal (“jackknife” data sets).
Typical uncertainties are ∼0.5% for the white noise, between 5 and 10% for the slope, and between 10 and 20% for the knee frequency.
White Noise Sensitivity[edit]
Details of the white noise sensitivity can be found in Planck-Early-III[19].
Table 2 summarizes the sensitivity numbers calculated during the first year of operations using methods and procedures described in detail in Planck-Early-V[8], compared with scientific requirements. The measured sensitivity is in very good agreement with pre-launch expectations. While the white noise moderately exceeds the design specification, this performance is fully in line with the LFI science objectives.
| Channel | Measurement [K s] | Requirement [K s] |
|---|---|---|
| 70 GHz | 152.5 | 119 |
| 44 GHz | 173.1 | 119 |
| 30 GHz | 146.8 | 119 |
Instrument Technical Performance[edit]
Spectral Response[edit]
The in-band receiver response has been thoroughly modelled and measured for all the LFI detectors during ground tests. The complete set of bandpass curves has been published in [21] where all the details of the LFI radiometer's spectral response are given. From each curve we have derived the effective centre frequency according to:
where is the receiver bandwidth and is the bandpass response. Details about colour corrections, , needed to derive the brightness temperature of a source with a power-law spectral index , are provided in Planck-Early-V[8].
Some details are also given in the corresponding section of the Annexes.
Bandpass Estimation[edit]
As detailed in [21], our most accurate method to measure the LFI bandpasses is based on measurements of individual components integrated into the LFI Advanced RF Model (LARFM) to yield a synthesised radiometer bandpass. The LARFM is a software tool based on the open-source Quasi Universal Circuit Simulator (QUCS). The measured frequency responses of the various subsystems (feed-OMT, FEM, BEM) are considered as lumped S-parameter components. Measurements of single components are obtained with standard methods and provide highly reliable results, with precision of order 0.1-0.2 dB over the entire band. Waveguides are simulated with an analytical model, in order to reproduce the effect of their temperature gradient and the effect of standing waves caused by impedance mismatch at the interfaces between the FEM and BEM. This is because the 1.8-meter long waveguides were not measured at unit level in cryogenic conditions. The model provides accurate agreement with the measured waveguide response in the conditions of the test measurements (300 K). The composite bandpasses are estimated to have a precision of about 1.5 to 2 dB.
Some details are also given in the corresponding section of the Annexes.
Stability[edit]
Thanks to its differential scheme, the LFI is insensitive to many effects caused by 1/f noise, thermal fluctuations, or electrical instabilities. As detailed in Planck-Early-III[19], one effect detected during the first survey was the daily temperature fluctuation in the back-end unit induced by the downlink transponder, which was powered on each day for downlinks during the first 258 days of the mission. As expected, the effect is highly correlated between the sky and reference load signals. In the difference, the variation is reduced by a factor , where is the gain modulation factor defined above (see eq. \ref{eq:erre1}).
A particular class of signal fluctuations occasionally observed during operations is due to electrical instabilities that appear as abrupt increases in the measured drain current of the front-end amplifiers, with a relaxation time variable from few seconds to some hundreds of seconds. Typically, these events cause a simultaneous change in the sky and reference load signals. Because they are essentially common-mode, their residual on the differenced data is negligible, and the data are suitable for science production. In a few cases the residual fluctuation in the differential output was large enough (a few millikelvin in calibrated antenna temperature units) to be flagged, and the data were not used. The total amount of discarded data for all LFI channels until Operational Day 389 was about 2000 s per detector, or 0.008%.
A further peculiar effect appeared in the 44 GHz detectors, where single isolated samples, either on the sky or the reference voltage output, were far from the rest. Over a reference period of four months, 15 occurrences of single-sample spikes (out of 24 total anomaly events) were discarded, an insignificant loss of data.
Thermal Susceptibility[edit]
As mentioned in section LFI In-flight Calibration above and detailed in [18], during the CPV campaign, susceptibility tests were performed in order to characterise the LFI instrument susceptibility to thermal and electrical variations.
The effect of temperature fluctuations on the LFI radiometers is originated in the Planck cold end interface of the hydrogen sorption cooler to the instrument focal plane. The temperature is actively controlled through a dedicated stage, the Thermal Stabilization Assembly (TSA), providing a first reduction of the effect. The thermal mass of the focal plane strongly contribute to reduce residual fluctuations. The physical temperature fluctuations propagated at the front end modules cause a correlated fluctuation in the radiometer signal degrading the quality of scientific data. The accurate characterization of this effect is crucial for possibly removing it from raw data by exploiting the housekeeping information of thermal sensors.
The propagation of the temperature oscillations through the focal plane and the instrument response to thermal changes were characterized through two main tests:
- the thermal dynamic response aimed at measuring the dynamic thermal behaviour of the LFI Focal Plane;
- the radiometers thermal susceptibility.
Some details are also given in the corresponding section of the Annexes.
Instrument Budgets[edit]
LFI power, mass and telemetry budget are given in the corresponding section of the Annexes.
Systematic Effects [edit]
The LFI design was driven by the need to suppress systematic effects well below instrument white noise. The differential receiver scheme, with reference loads cooled to 4 K, greatly minimises the effect of 1/f noise and common-mode fluctuations, such as thermal perturbations in the 20K LFI focal plane. The use of a gain modulation factor (see Eq. \ref{eq:erre1} in RCA section above) largely compensates for spurious contributions from input offsets. Furthermore, diode averaging (Eq. \ref{eq:v1} in RCA section above) allows us to cancel second-order correlations such as those originating from phase switch imbalances.
We have developed an error budget for systematic effects Planck-PreLaunch-II[7]Planck-Early-III[19]Planck-2013-III[22] as a reference for both instrument design and data analysis. Our goal is to ensure that each systematic effect is rejected to the specified level, either by design or by robust removal in software. At this stage, the following effects are relevant:
- – 1/f noise;
- – 1 Hz frequency spikes;
- – receivers non-linearities;
- – thermal fluctuations in the back-end modules driven by temperature oscillations from the transponder during the first survey;
- – thermal fluctuations in the 20 K focal plane;
- – thermal fluctuations of the 4 K reference loads.
For each of these effects we used flight data and information from ground tests to build timelines, maps, and angular power spectra that represent our best knowledge of their impact on the scientific analysis. The details of the systematic effect analysis is given in section LFI data processing section - Systematic Effects uncertainties.
The Sorption Cooler[edit]
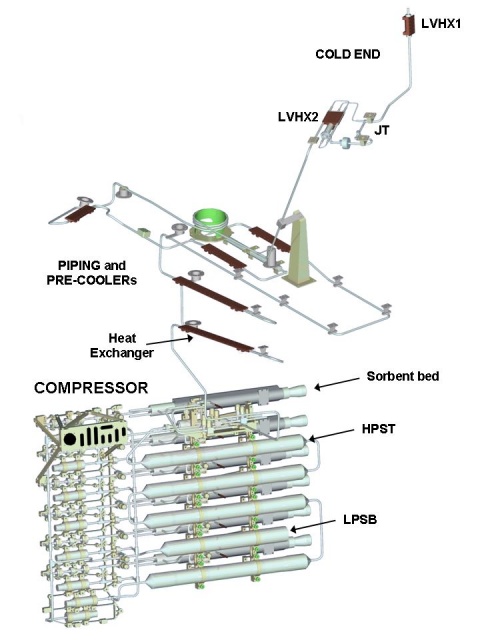
The Planck H2 Sorption Cooler is the first stage of the active cryogenic chain: its task is to maintain the LFI down to the operating temperature while providing a pre-cooling stage for the HFI refrigerators. The system performs a simple thermodynamic cycle based on hydrogen compression, gas pre-cooling by three passive radiators, further cooling due to the heat recovery by the cold low pressure gas stream, expansion through a J-T valve and evaporation at the cold stage Planck-Early-II[16]. A drawing of the Planck Sorption Cooler System (SCS) is shown in Fig. 5. The engine of the cryocooler is the compressor. It serves two main functions: to produce the high-pressure hydrogen gas flow and to maintain a stable gas recovery rate, which keeps the return pressure, hence the liquid temperature, constant. The high pressure gas flowing to the cold end is pre-cooled by exchanging heat with the three passive stages at the V-Grooves and with the evaporated cold gas returning back to the compressor. The gas then expands at the cold end through a J-T valve producing approximately 1 Watt of cooling power at a temperature of <20K: most of this heat lift is used at the LVHX2 (Liquid Vapour Heat eXchanger 2, see Fig. 5) interface to absorb the LFI heat load at a temperature around 20K. The remaining heat lift is used at the LVHX1 as a pre-cooling stage, at a temperature lower than 19 K, for the two HFI refrigerators. The cooler and its performance are described in detail in [23].
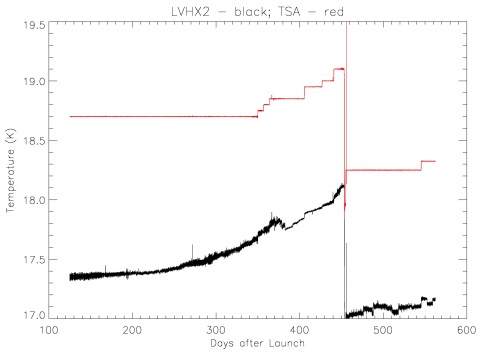
Both LVHX’s provide a temperature around 18 K, with fluctuations driven by the cooler instabilities (compressor element variations, cycling, two phase flow dynamics etc.). Stabilization of the HFI interface (LVHX1) temperature is not necessary, as thermal control of the subsequent colder stages is more efficient and very effective. To reduce cold end fluctuations directly transmitted to the LFI radiometers, a copper block designated as the Temperature Stabilization Assembly (TSA), is inserted, as an intermediate stage, between LVHX2 and the LFI FocaL Plane Unit (FPU). The TSA comprises a temperature sensor and a heater controlled by a PID-type feedback loop working in combination with the passive thermal inertia. The set-point temperature of the TSA is an adjustable parameter of the sorption cooler system, chosen to provide dynamic range for control during mission: as the compressor elements age, the return gas pressure and thus the temperature of LVHX2 rise slowly. To keep the LFI T reference stable during operations the set point must be periodically adjusted to maintain the level of oscillations within the required range (Fig. 6).
Two sorption cooler units have been integrated on board the Planck spacecraft. Both units have been used to cover the mission lifetime: one cooler has been operated for the first two sky surveys. At the end of its lifetime a switchover operation, performed on August 11th 2010 (455 days after launch), has activated the second unit that has been running since then. The LVHX2 temperature change due to the new cooler start, and the subsequent re-adjustment of the LFI temperature stabilization stage, is clear in Fig. 6.
References[edit]
- ↑ 1.01.1 The Planck-LFI flight model composite waveguides, O. D'Arcangelo, L. Figini, A. Simonetto, F. Villa, M. Pecora, P. Battaglia, M. Bersanelli, R. C. Butler, F. Cuttaia, S. Garavaglia, P. Guzzi, N. Mandolesi, A. Mennella, G. Morgante, L. Pagan, L. Valenziano, Journal of Instrumentation, 4, 2007-+, (2009).
- ↑ 2.02.1 Planck-LFI: design and performance of the 4 Kelvin Reference Load Unit, L. Valenziano, F. Cuttaia, A. De Rosa, L. Terenzi, A. Brighenti, G. P. Cazzola, A. Garbesi, S. Mariotti, G. Orsi, L. Pagan, F. Cavaliere, M. Biggi, R. Lapini, E. Panagin, P. Battaglia, R. C. Butler, M. Bersanelli, O. D'Arcangelo, S. Levin, N. Mandolesi, A. Mennella, G. Morgante, G. Morigi, M. Sandri, A. Simonetto, M. Tomasi, F. Villa, M. Frailis, S. Galeotta, A. Gregorio, R. Leonardi, S. R. Lowe, M. Maris, P. Meinhold, L. Mendes, L. Stringhetti, A. Zonca, A. Zacchei, Journal of Instrumentation, 4, 2006-+, (2009).
- ↑ 3.03.1 The Planck-LFI Radiometer Electronics Box Assembly, J. M. Herreros, M. F. Gómez, R. Rebolo, H. Chulani, J. A. Rubiño-Martin, S. R. Hildebrandt, M. Bersanelli, R. C. Butler, M. Miccolis, A. Peña, M. Pereira, F. Torrero, C. Franceschet, M. López, C. Alcalá, Journal of Instrumentation, 4, 2008-+, (2009).
- ↑ 4.04.1 Optimization of Planck-LFI on-board data handling, M. Maris, M. Tomasi, S. Galeotta, M. Miccolis, S. Hildebrandt, M. Frailis, R. Rohlfs, N. Morisset, A. Zacchei, M. Bersanelli, P. Binko, C. Burigana, R. C. Butler, F. Cuttaia, H. Chulani, O. D'Arcangelo, S. Fogliani, E. Franceschi, F. Gasparo, F. Gomez, A. Gregorio, J. M. Herreros, R. Leonardi, P. Leutenegger, G. Maggio, D. Maino, M. Malaspina, N. Mandolesi, P. Manzato, M. Meharga, P. Meinhold, A. Mennella, F. Pasian, F. Perrotta, R. Rebolo, M. Türler, A. Zonca, Journal of Instrumentation, 4, 2018-+, (2009).
- ↑ 5.05.1 1/f noise and other systematic effects in the Planck-LFI radiometers, M. Seiffert, A. Mennella, C. Burigana, N. Mandolesi, M. Bersanelli, P. Meinhold, P. Lubin, A&A, 391, 1185-1197, (2002).
- ↑ 6.06.1 Offset balancing in pseudo-correlation radiometers for CMB measurements, A. Mennella, M. Bersanelli, M. Seiffert, D. Kettle, N. Roddis, A. Wilkinson, P. Meinhold, A&A, 410, 1089-1100, (2003).
- ↑ 7.07.1 Planck pre-launch status: Design and description of the Low Frequency Instrument, M. Bersanelli, N. Mandolesi, R. C. Butler, A. Mennella, F. Villa, B. Aja, E. Artal, E. Artina, C. Baccigalupi, M. Balasini, G. Baldan, A. Banday, P. Bastia, P. Battaglia, T. Bernardino, E. Blackhurst, L. Boschini, C. Burigana, G. Cafagna, B. Cappellini, F. Cavaliere, F. Colombo, G. Crone, F. Cuttaia, O. D'Arcangelo, L. Danese, R. D. Davies, R. J. Davis, L. de Angelis, G. C. de Gasperis, L. de La Fuente, A. de Rosa, G. de Zotti, M. C. Falvella, F. Ferrari, R. Ferretti, L. Figini, S. Fogliani, C. Franceschet, E. Franceschi, T. Gaier, S. Garavaglia, F. Gomez, K. Gorski, A. Gregorio, P. Guzzi, J. M. Herreros, S. R. Hildebrandt, R. Hoyland, N. Hughes, M. Janssen, P. Jukkala, D. Kettle, V. H. Kilpiä, M. Laaninen, P. M. Lapolla, C. R. Lawrence, D. Lawson, J. P. Leahy, R. Leonardi, P. Leutenegger, S. Levin, P. B. Lilje, S. R. Lowe, P. M. Lubin, D. Maino, M. Malaspina, M. Maris, J. Marti-Canales, E. Martinez-Gonzalez, A. Mediavilla, P. Meinhold, M. Miccolis, G. Morgante, P. Natoli, R. Nesti, L. Pagan, C. Paine, B. Partridge, J. P. Pascual, F. Pasian, D. Pearson, M. Pecora, F. Perrotta, P. Platania, M. Pospieszalski, T. Poutanen, M. Prina, R. Rebolo, N. Roddis, J. A. Rubiño-Martin, M. J. Salmon, M. Sandri, M. Seiffert, R. Silvestri, A. Simonetto, P. Sjoman, G. F. Smoot, C. Sozzi, L. Stringhetti, E. Taddei, J. Tauber, L. Terenzi, M. Tomasi, J. Tuovinen, L. Valenziano, J. Varis, N. Vittorio, L. A. Wade, A. Wilkinson, F. Winder, A. Zacchei, A. Zonca, A&A, 520, A4+, (2010).
- ↑ 8.08.18.28.38.48.5 Planck early results. V. The Low Frequency Instrument data processing, A. Zacchei, D. Maino, C. Baccigalupi, M. Bersanelli, A. Bonaldi, L. Bonavera, C. Burigana, R. C. Butler, F. Cuttaia, G. de Zotti, J. Dick, M. Frailis, S. Galeotta, J. González-Nuevo, K. M. Górski, A. Gregorio, E. Keihänen, R. Keskitalo, J. Knoche, H. Kurki-Suonio, C. R. Lawrence, S. Leach, J. P. Leahy, M. López-Caniego, N. Mandolesi, M. Maris, F. Matthai, P. R. Meinhold, A. Mennella, G. Morgante, N. Morisset, P. Natoli, F. Pasian, F. Perrotta, G. Polenta, T. Poutanen, M. Reinecke, S. Ricciardi, R. Rohlfs, M. Sandri, A.-S. Suur-Uski, J. A. Tauber, D. Tavagnacco, L. Terenzi, M. Tomasi, J. Valiviita, F. Villa, A. Zonca, A. J. Banday, R. B. Barreiro, J. G. Bartlett, N. Bartolo, L. Bedini, K. Bennett, P. Binko, J. Borrill, F. R. Bouchet, M. Bremer, P. Cabella, B. Cappellini, X. Chen, L. Colombo, M. Cruz, A. Curto, L. Danese, R. D. Davies, R. J. Davis, G. de Gasperis, A. de Rosa, G. de Troia, C. Dickinson, J. M. Diego, S. Donzelli, U. Dörl, G. Efstathiou, T. A. Enßlin, H. K. Eriksen, M. C. Falvella, F. Finelli, E. Franceschi, T. C. Gaier, F. Gasparo, R. T. Génova-Santos, G. Giardino, F. Gómez, A. Gruppuso, F. K. Hansen, R. Hell, D. Herranz, W. Hovest, M. Huynh, J. Jewell, M. Juvela, T. S. Kisner, L. Knox, A. Lähteenmäki, J.-M. Lamarre, R. Leonardi, J. León-Tavares, P. B. Lilje, P. M. Lubin, G. Maggio, D. Marinucci, E. Martínez-González, M. Massardi, S. Matarrese, M. T. Meharga, A. Melchiorri, M. Migliaccio, S. Mitra, A. Moss, H. U. Nørgaard-Nielsen, L. Pagano, R. Paladini, D. Paoletti, B. Partridge, D. Pearson, V. Pettorino, D. Pietrobon, G. Prézeau, P. Procopio, J.-L. Puget, C. Quercellini, J. P. Rachen, R. Rebolo, G. Robbers, G. Rocha, J. A. Rubiño-Martín, E. Salerno, M. Savelainen, D. Scott, M. D. Seiffert, J. I. Silk, G. F. Smoot, J. Sternberg, F. Stivoli, R. Stompor, G. Tofani, L. Toffolatti, J. Tuovinen, M. Türler, G. Umana, P. Vielva, N. Vittorio, C. Vuerli, L. A. Wade, R. Watson, S. D. M. White, A. Wilkinson, A&A, 536, A5, (2011).
- ↑ Planck-LFI flight model feed horns, F. Villa, O. D'Arcangelo, M. Pecora, L. Figini, R. Nesti, A. Simonetto, C. Sozzi, M. Sandri, P. Battaglia, P. Guzzi, M. Bersanelli, R. C. Butler, N. Mandolesi, Journal of Instrumentation, 4, 2004-+, (2009).
- ↑ The Planck-LFI flight model ortho-mode transducers, O. D'Arcangelo, A. Simonetto, L. Figini, E. Pagana, F. Villa, M. Pecora, P. Battaglia, M. Bersanelli, R. C. Butler, S. Garavaglia, P. Guzzi, N. Mandolesi, C. Sozzi, Journal of Instrumentation, 4, 2005-+, (2009).
- ↑ 11.011.1 Design, development, and verification of the Planck Low Frequency Instrument 70 GHz Front-End and Back-End Modules, J. Varis, N. J. Hughes, M. Laaninen, V.-H. Kilpiä, P. Jukkala, J. Tuovinen, S. Ovaska, P. Sjöman, P. Kangaslahti, T. Gaier, R. Hoyland, P. Meinhold, A. Mennella, M. Bersanelli, R. C. Butler, F. Cuttaia, E. Franceschi, R. Leonardi, P. Leutenegger, M. Malaspina, N. Mandolesi, M. Miccolis, T. Poutanen, H. Kurki-Suonio, M. Sandri, L. Stringhetti, L. Terenzi, M. Tomasi, L. Valenziano, Journal of Instrumentation, 4, 2001-+, (2009).
- ↑ LFI 30 and 44 GHz receivers Back-End Modules, E. Artal, B. Aja, M. L. de la Fuente, J. P. Pascual, A. Mediavilla, E. Martinez-Gonzalez, L. Pradell, P. de Paco, M. Bara, E. Blanco, E. García, R. Davis, D. Kettle, N. Roddis, A. Wilkinson, M. Bersanelli, A. Mennella, M. Tomasi, R. C. Butler, F. Cuttaia, N. Mandolesi, L. Stringhetti, Journal of Instrumentation, 4, 2003-+, (2009).
- ↑ Design, development and verification of the 30 and 44 GHz front-end modules for the Planck Low Frequency Instrument, R. J. Davis, A. Wilkinson, R. D. Davies, W. F. Winder, N. Roddis, E. J. Blackhurst, D. Lawson, S. R. Lowe, C. Baines, M. Butlin, A. Galtress, D. Shepherd, B. Aja, E. Artal, M. Bersanelli, R. C. Butler, C. Castelli, F. Cuttaia, O. D'Arcangelo, T. Gaier, R. Hoyland, D. Kettle, R. Leonardi, N. Mandolesi, A. Mennella, P. Meinhold, M. Pospieszalski, L. Stringhetti, M. Tomasi, L. Valenziano, A. Zonca, Journal of Instrumentation, 4, 2002-+, (2009).
- ↑ 14.014.1 Planck pre-launch status: Calibration of the Low Frequency Instrument flight model radiometers, F. Villa, L. Terenzi, M. Sandri, P. Meinhold, T. Poutanen, P. Battaglia, C. Franceschet, N. Hughes, M. Laaninen, P. Lapolla, M. Bersanelli, R. C. Butler, F. Cuttaia, O. D'Arcangelo, M. Frailis, E. Franceschi, S. Galeotta, A. Gregorio, R. Leonardi, S. R. Lowe, N. Mandolesi, M. Maris, L. Mendes, A. Mennella, G. Morgante, L. Stringhetti, M. Tomasi, L. Valenziano, A. Zacchei, A. Zonca, B. Aja, E. Artal, M. Balasini, T. Bernardino, E. Blackhurst, L. Boschini, B. Cappellini, F. Cavaliere, A. Colin, F. Colombo, R. J. Davis, L. de La Fuente, J. Edgeley, T. Gaier, A. Galtress, R. Hoyland, P. Jukkala, D. Kettle, V.-H. Kilpia, C. R. Lawrence, D. Lawson, J. P. Leahy, P. Leutenegger, S. Levin, D. Maino, M. Malaspina, A. Mediavilla, M. Miccolis, L. Pagan, J. P. Pascual, F. Pasian, M. Pecora, M. Pospieszalski, N. Roddis, M. J. Salmon, M. Seiffert, R. Silvestri, A. Simonetto, P. Sjoman, C. Sozzi, J. Tuovinen, J. Varis, A. Wilkinson, F. Winder, A&A, 520, A6+, (2010).
- ↑ 15.015.115.215.3 Planck pre-launch status: Low Frequency Instrument calibration and expected scientific performance, A. Mennella, M. Bersanelli, R. C. Butler, F. Cuttaia, O. D'Arcangelo, R. J. Davis, M. Frailis, S. Galeotta, A. Gregorio, C. R. Lawrence, R. Leonardi, S. R. Lowe, N. Mandolesi, M. Maris, P. Meinhold, L. Mendes, G. Morgante, M. Sandri, L. Stringhetti, L. Terenzi, M. Tomasi, L. Valenziano, F. Villa, A. Zacchei, A. Zonca, M. Balasini, C. Franceschet, P. Battaglia, P. M. Lapolla, P. Leutenegger, M. Miccolis, L. Pagan, R. Silvestri, B. Aja, E. Artal, G. Baldan, P. Bastia, T. Bernardino, L. Boschini, G. Cafagna, B. Cappellini, F. Cavaliere, F. Colombo, L. de La Fuente, J. Edgeley, M. C. Falvella, F. Ferrari, S. Fogliani, E. Franceschi, T. Gaier, F. Gomez, J. M. Herreros, S. Hildebrandt, R. Hoyland, N. Hughes, P. Jukkala, D. Kettle, M. Laaninen, D. Lawson, P. Leahy, S. Levin, P. B. Lilje, D. Maino, M. Malaspina, P. Manzato, J. Marti-Canales, E. Martinez-Gonzalez, A. Mediavilla, F. Pasian, J. P. Pascual, M. Pecora, L. Peres-Cuevas, P. Platania, M. Pospieszalsky, T. Poutanen, R. Rebolo, N. Roddis, M. Salmon, M. Seiffert, A. Simonetto, C. Sozzi, J. Tauber, J. Tuovinen, J. Varis, A. Wilkinson, F. Winder, A&A, 520, A5+, (2010).
- ↑ 16.016.1 Planck early results. II. The thermal performance of Planck, Planck Collaboration II, A&A, 536, A2, (2011).
- ↑ Noise properties of the Planck-LFI receivers, P. Meinhold, R. Leonardi, B. Aja, E. Artal, P. Battaglia, M. Bersanelli, E. Blackhurst, C. R. Butler, L. P. Cuevas, F. Cuttaia, O. D'Arcangelo, R. Davis, M. L. de la Fuente, M. Frailis, C. Franceschet, E. Franceschi, T. Gaier, S. Galeotta, A. Gregorio, R. Hoyland, N. Hughes, P. Jukkala, D. Kettle, M. Laaninen, P. Leutenegger, S. R. Lowe, M. Malaspina, R. Mandolesi, M. Maris, E. Martínez-González, L. Mendes, A. Mennella, M. Miccolis, G. Morgante, N. Roddis, M. Sandri, M. Seiffert, M. Salmón, L. Stringhetti, T. Poutanen, L. Terenzi, M. Tomasi, J. Tuovinen, J. Varis, L. Valenziano, F. Villa, A. Wilkinson, F. Winder, A. Zacchei, A. Zonca, Journal of Instrumentation, 4, 2009-+, (2009).
- ↑ 18.018.1 In-flight calibration and verification of the Planck-LFI instrument, A. Gregorio, F. Cuttaia, A. Mennella, M. Bersanelli, S. Maris, P. Meinhold, Submitted to Journal of Instrumentation, (2013).
- ↑ 19.019.119.219.319.4 Planck early results. III. First assessment of the Low Frequency Instrument in-flight performance, A. Mennella, R. C. Butler, A. Curto, F. Cuttaia, R. J. Davis, J. Dick, M. Frailis, S. Galeotta, A. Gregorio, H. Kurki-Suonio, C. R. Lawrence, S. Leach, J. P. Leahy, S. Lowe, D. Maino, N. Mandolesi, M. Maris, E. Martínez-González, P. R. Meinhold, G. Morgante, D. Pearson, F. Perrotta, G. Polenta, T. Poutanen, M. Sandri, M. D. Seiffert, A.-S. Suur-Uski, D. Tavagnacco, L. Terenzi, M. Tomasi, J. Valiviita, F. Villa, R. Watson, A. Wilkinson, A. Zacchei, A. Zonca, B. Aja, E. Artal, C. Baccigalupi, A. J. Banday, R. B. Barreiro, J. G. Bartlett, N. Bartolo, P. Battaglia, K. Bennett, A. Bonaldi, L. Bonavera, J. Borrill, F. R. Bouchet, C. Burigana, P. Cabella, B. Cappellini, X. Chen, L. Colombo, M. Cruz, L. Danese, O. D'Arcangelo, R. D. Davies, G. de Gasperis, A. de Rosa, G. de Zotti, C. Dickinson, J. M. Diego, S. Donzelli, G. Efstathiou, T. A. Enßlin, H. K. Eriksen, M. C. Falvella, F. Finelli, S. Foley, C. Franceschet, E. Franceschi, T. C. Gaier, R. T. Génova-Santos, D. George, F. Gómez, J. González-Nuevo, K. M. Górski, A. Gruppuso, F. K. Hansen, D. Herranz, J. M. Herreros, R. J. Hoyland, N. Hughes, J. Jewell, P. Jukkala, M. Juvela, P. Kangaslahti, E. Keihänen, R. Keskitalo, V.-H. Kilpia, T. S. Kisner, J. Knoche, L. Knox, M. Laaninen, A. Lähteenmäki, J.-M. Lamarre, R. Leonardi, J. León-Tavares, P. Leutenegger, P. B. Lilje, M. López-Caniego, P. M. Lubin, M. Malaspina, D. Marinucci, M. Massardi, S. Matarrese, F. Matthai, A. Melchiorri, L. Mendes, M. Miccolis, M. Migliaccio, S. Mitra, A. Moss, P. Natoli, R. Nesti, H. U. Nørgaard-Nielsen, L. Pagano, R. Paladini, D. Paoletti, B. Partridge, F. Pasian, V. Pettorino, D. Pietrobon, M. Pospieszalski, G. Prézeau, M. Prina, P. Procopio, J.-L. Puget, C. Quercellini, J. P. Rachen, R. Rebolo, M. Reinecke, S. Ricciardi, G. Robbers, G. Rocha, N. Roddis, J. A. Rubiño-Martín, M. Savelainen, D. Scott, R. Silvestri, A. Simonetto, P. Sjoman, G. F. Smoot, C. Sozzi, L. Stringhetti, J. A. Tauber, G. Tofani, L. Toffolatti, J. Tuovinen, M. Türler, G. Umana, L. Valenziano, J. Varis, P. Vielva, N. Vittorio, L. A. Wade, C. Watson, S. D. M. White, F. Winder, A&A, 536, A3, (2011).
- ↑ Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results, G. Hinshaw, J. L. Weiland, R. S. Hill, N. Odegard, D. Larson, C. L. Bennett, J. Dunkley, B. Gold, M. R. Greason, N. Jarosik, E. Komatsu, M. R. Nolta, L. Page, D. N. Spergel, E. Wollack, M. Halpern, A. Kogut, M. Limon, S. S. Meyer, G. S. Tucker, E. L. Wright, ApJS, 180, 225-245, (2009).
- ↑ 21.021.1 Planck-LFI radiometers' spectral response, A. Zonca, C. Franceschet, P. Battaglia, F. Villa, A. Mennella, O. D'Arcangelo, R. Silvestri, M. Bersanelli, E. Artal, R. C. Butler, F. Cuttaia, R. J. Davis, S. Galeotta, N. Hughes, P. Jukkala, V.-H. Kilpiä, M. Laaninen, N. Mandolesi, M. Maris, L. Mendes, M. Sandri, L. Terenzi, J. Tuovinen, J. Varis, A. Wilkinson, Journal of Instrumentation, 4, 2010-+, (2009).
- ↑ Planck 2013 results. III. Low Frequency Instrument systematic uncertainties, Planck Collaboration, 2014, A&A, 571, A3
- ↑ Cryogenic characterization of the Planck sorption cooler system flight model, G. Morgante, D. Pearson, F. Melot, P. Stassi, L. Terenzi, P. Wilson, B. Hernandez, L. Wade, A. Gregorio, M. Bersanelli, C. Butler, N. Mandolesi, Journal of Instrumentation, 4, 2016-+, (2009).
(Planck) Low Frequency Instrument
LFI warm electronics Back End Unit
High Electron Mobility Transistor
(Planck) High Frequency Instrument
LFI Radiometer Array Assembly
Sorption Cooler Subsystem (Planck)
LFI Radiometer Electronics Box Assembly
LFI cryogenic amplifying stage Front End Unit
Service Module
Sorption Cooler Compressor assembly
Focal Plane Unit
LFI warm electronics Back End Module
LFI Data Acquisition Electronics
revolutions per minute
LFI Radiometer Chain Assembly
LFI cryogenic amplifying stage Front End Module
LFI Ortho Module Transducer
analog to digital converter
Feed Horn
LFI Waveguide
Data Processing Unit
Signal Processing Unit
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
System Level Test
Centre Spatial de Liège
Calibration and Performance Verification
Line Of Sight
Full-Width-at-Half-Maximum
Cosmic Microwave background
hermal Stabilization Assembly
House Keeping