Difference between revisions of "HFI design, qualification, and performance"
| Line 327: | Line 327: | ||
| − | + | <gallery caption="Reference bolometer spectra and S/N." widths="300px" heights="300px" perrow="3"> | |
| − | + | File:BREF_LowF_Apod5_avgSpec_SN_sm.png|100 - 217 GHz | |
| − | + | File:BREF_HighF_Apod5_avgSpec_SN_sm.png|353 - 857 GHz | |
| − | + | File:Bref_LowF_HighF_SN_sm.png|all bands | |
| − | + | </gallery> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<gallery caption="Reference bolometer spectra (top) and S/N (bottom) for each of the HFI bands (vertical bars represent band edges)." widths="300px" heights="300px" perrow="3"> | <gallery caption="Reference bolometer spectra (top) and S/N (bottom) for each of the HFI bands (vertical bars represent band edges)." widths="300px" heights="300px" perrow="3"> | ||
| Line 348: | Line 343: | ||
| − | [[Image:SNall_sm.png| | + | [[Image:SNall_sm.png|x300px|alt=image]] |
==== Out-of-Band Spectral Transmission Content ==== | ==== Out-of-Band Spectral Transmission Content ==== | ||
| Line 357: | Line 352: | ||
The normalized ratioed spectrum and filter are both scaled by the optical efficiency (see §[sec:EFF]). For the 100 - 353 bands, the filter spectrum is also scaled by <math>\lambda^2</math> to account for single-moded throughput normalization. This frequency scaling results in a more accurate in- and near-band match between the two sets of spectra, at the cost of less accuracy at much higher frequencies where any transmission will not be single-moded. As ransmission at higher frequencies is significantly reduced, this trade-off is acceptable. The 545 and 857 GHz bands have their filter spectra without the additional frequency scaling as this is not correct for multi-moded propagation. Both lower and upper frequency thresholds, <math>\nu_{l}</math>, and <math>\nu_{u}</math>, are defined for each band, below and above which the IAS-FTS spectra and/or the Cardiff composite filter spectra must be used, respectively. This is done to avoid introducing any detector nonlinearity residuals into the final spectral transmission data products. The region between these two points is defined as the transition region; within this region the amplitudes and slopes of the IAS and filter spectra are used to determine the spectral cross-oveer/transition point. Additional checks are performed to ensure that non-physical data processing artefacts are not introduced into the spectral transition region. Additionally, a similar technique is used, with decreasing frequency instead of increasing, for the 545 and 857 GHz bands with a filter-induced frequency cut-on. Figure [fig:OOBex] illustrates an example of both the FTS and filter spectra used in extending the transmission profiles beyond the HFI optical bands. Similar plots for every detector are shown in §[sec:stitch]. | The normalized ratioed spectrum and filter are both scaled by the optical efficiency (see §[sec:EFF]). For the 100 - 353 bands, the filter spectrum is also scaled by <math>\lambda^2</math> to account for single-moded throughput normalization. This frequency scaling results in a more accurate in- and near-band match between the two sets of spectra, at the cost of less accuracy at much higher frequencies where any transmission will not be single-moded. As ransmission at higher frequencies is significantly reduced, this trade-off is acceptable. The 545 and 857 GHz bands have their filter spectra without the additional frequency scaling as this is not correct for multi-moded propagation. Both lower and upper frequency thresholds, <math>\nu_{l}</math>, and <math>\nu_{u}</math>, are defined for each band, below and above which the IAS-FTS spectra and/or the Cardiff composite filter spectra must be used, respectively. This is done to avoid introducing any detector nonlinearity residuals into the final spectral transmission data products. The region between these two points is defined as the transition region; within this region the amplitudes and slopes of the IAS and filter spectra are used to determine the spectral cross-oveer/transition point. Additional checks are performed to ensure that non-physical data processing artefacts are not introduced into the spectral transition region. Additionally, a similar technique is used, with decreasing frequency instead of increasing, for the 545 and 857 GHz bands with a filter-induced frequency cut-on. Figure [fig:OOBex] illustrates an example of both the FTS and filter spectra used in extending the transmission profiles beyond the HFI optical bands. Similar plots for every detector are shown in §[sec:stitch]. | ||
| − | [[Image:OOBstitch_bc00_Prad_Apod5_v302_sm.png| | + | [[Image:OOBstitch_bc00_Prad_Apod5_v302_sm.png|x300px|alt=image]] |
==== Waveguide Model ==== | ==== Waveguide Model ==== | ||
| Line 571: | Line 566: | ||
|} | |} | ||
| − | [[Image:COflags_sm.png| | + | [[Image:COflags_sm.png|x300px|alt=image]] |
| − | [[Image: | + | [[Image:COJ10_HFI100_SpecTrans_v300_Apod5_sm.png|x300px|alt=image]] |
Revision as of 01:29, 16 January 2013
THIS SECTION IS CURRENTLY IN A VERY PRELIMINARY FORM. It is intended to provide an overview of the instrument and of its different sub-systems. Two papers that include and detail this information are available: LAMARRE, Jean-Michel, PUGET, Jean-Loup et 93 co-auteurs, " Planck pre-launch status: The HFI instrument, from specification to actual performance", Astronomy and Astrophysics, Volume 520, id.A9 (20 pages, A&A Homepage), 09/2010. and Planck-HFI Core Team and 165 co-authors. " Planck early results. IV. First assessment of the High Frequency Instrument in-flight performance", Astronomy & Astrophysics, Volume 536, id.A4 (A&A Homepage) 12/2011." Additional detailed information potentially useful for the use of the HFI data will be included into this section or annexed to it.
Contents
- 1 HFI high level description and Architecture
- 2 Cryogenics
- 3 Cold optics
- 3.1 Horns,lenses
- 3.2 Spectral Characterization of the HFI Detector Focal Plane
- 3.2.1 Additional Experiments
- 3.2.2 Filter Measurements
- 3.2.3 Data Processing and Fourier Transformation
- 3.2.4 Reference Bolometer Spectra
- 3.2.5 Out-of-Band Spectral Transmission Content
- 3.2.6 Waveguide Model
- 3.2.7 Optical Efficiency
- 3.2.8 CO interpolation
- 3.2.9 Spectral Response Conclusions and Conformity With Requirements
- 4 Detection chain
- 5 Operations
- 6 System (Ken)
- 7 Summary
- 8 Annexes
HFI high level description and Architecture[edit]
(Lamarre/Pajot)
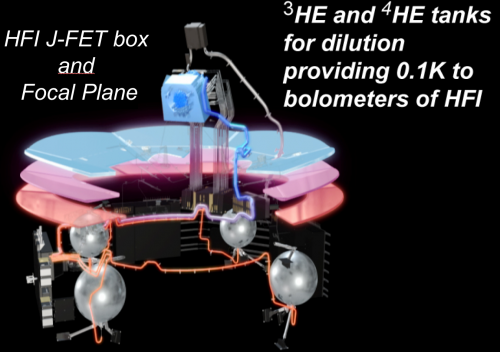
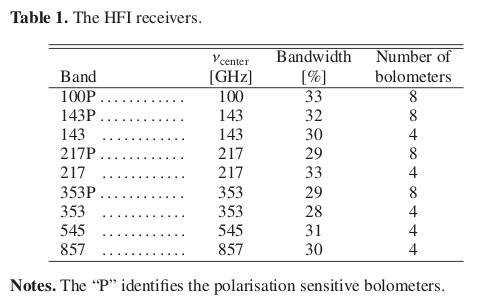
The HFI instrument is designed around 52 bolometers. Twenty of the bolometers (spider-web bolometers or SWBs) are sensitive to total power, and the remaining 32 units are arranged in pairs of orthogonally-oriented polarisation-sensitive bolometers (PSBs). All bolometers are operated at a temperature of ~0.1 K by mean of a space qualified dilution cooler coupled with a high precision temperature control system. A 4He-JT provides an active cooling for 4 K stages using vibration controlled mechanical compressors to prevent excessive warming of the 100 mK stage and minimize microphonic effects in the bolometers. Bolometers and sensitive thermometers are read using AC-bias scheme through JFET amplifiers operated at ~130 K that provide high sensitivity and low frequency stability. The HFI covers six bands centred at 100, 143, 217, 353, 545 and 857 GHz, thanks to a thermo-optical design consisting of three corrugated horns and a set of compact reflective filters and lenses at cryogenic temperatures.
The whole satellite is organized to provide thermal transitions between its warm part exposed to the sun and earth radiation, and the focal plane instruments that include the cold receivers (Sections XXX1 and XXX2). The various parts of the HFI are distributed among three different stages of the satellite in order to provide each sub-system an optimal operating temperature. The "warm" parts, including nearly all the electronics and the sources of fluids of the 4K and 0.1K coolers, are attached and thermally linked to the service module of the satellite. The first stage of the preamplifiers is attached to the back of the passively cooled telescope structure. The focal plane unit is attached to the 20K stage cooled by the sorption cooler. This is detailed in (XXX2).
The telescope and horns selects the geometrical origin of photons. They provide a high transmission efficiency to photons inside the main beam, while photons coming from the intermediate and far-side lobes have very low probability of being detected. This essential characteristics is known by a complex process mixing ground measurements of components (horns, reflectors), modelling the shape of the far side lobes, and measuring in-flight bright sources, especially planets.
The filters and bolometers define the spectral responses and absolute optical efficiency, that will be known mostly from ground based measurements performed at component, sub-system and system levels reported in this document. The relations between spectral response and geometrical response will also be addressed.
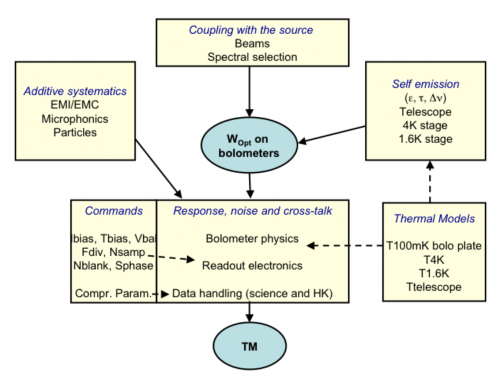
Photons absorbed by a bolometer include the thermal radiation emitted by the various optical devices: telescope, horns and filters. They are transformed in heat that propagates to the bolometer thermometer and influence its temperature which is itself measured by the readout electronics. Temperatures of all these items must stable enough not to contaminate the scientific signal delivered by the bolometers. How this stability is reached is described in section 2.4.1_cryogeny.
The bolometer temperature depends also on the temperature of the bolometer plate, on the intensity of the biasing current and on any spurious inputs, such as cosmic rays and mechanical vibrations. Such systematics are included in the list of section 2.4.1._systematics.
Since the bolometer thermometer is part of an active circuitry that also heats it, the response of this system is complex and has to be considered as a whole. In addition, due to the modulation of the bias current and to the sampling of the data, a complex time response is expected, which modifies the beam shape resulting from the scanning of point sources. Section 2.4.1._time response is dedicated to the description of the time response.
Figure 2.4.1.1_HFI signal formation: Logic of the formation of the signal in HFI. This is an idealized description of the physics that takes place in the instrument. The optical power that is absorbed by the bolometers comes from the observed sky and from the instrument itself. The bolometers and readout electronics, acting as a single and complex chain, transform this optical power in data that is compressed and transmitted for science data reduction.
Cryogenics[edit]
(F .Pajot)
Dilution[edit]
The HFI 3He-4He dilution cooler produces temperatures of 0.1 K for the bolometers through the dilution of 3He into 4He and 1.4 K through JT expansion of the 3He and 4He mixture. The dilution cooler is described in detail in section 2.3.3 of Planck early paper II .
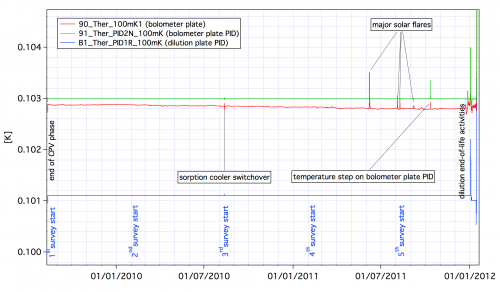
The dilution was operated with flows set to the minimum available values, and provided a total lifetime of 30.5 months, exceeding the nominal lifetime of 16 months by 14.5 months. The dilution stage was stabilized by a PID control with a regulating power between 20 and 30 nW providing a temperature close to 101 mK. The bolometer plate was stabilized at 102.8 mK with about 5 nW dissipated by PID regulation. The cooling power values were in very good agreement with those obtained during the ground tests and calibration. However, the cosmic particles interactions with the 100 mK stages induced temperature fluctuations and glitches on the thermometers measurements. The baseline correction of the bolometers signals from the 100 mK bolometer stage temperatures fluctuations is described in the TOI processing section.
At very low frequency, below 1 mHz, the temperature fluctuations are very well correlated with the high energy particles hit rate, as measured by the on-board monitor. At frequencies in the 10 mHz to 1 Hz range, single events inducing a global or partial temperature change of the bolometer plate are observed.
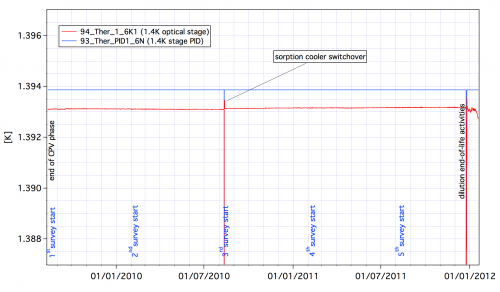
The 1.4K stage is very stable and given the very low coupling coefficients between the 1.4K optical components and the detectors no effect can be measured on the signal.
Detailed thermal analysis of the in-flight stability of the dilution cooler can be found in section 5.4 of Planck early paper II .
4K J-T cooler[edit]
The HFI 4K J-T cooler produces a temperature of 4K for the HFI 4K stage and optics and the precooling of the dilution gases. Full description of the 4K cooler can be found in in section 2.3.2 of Planck early paper II .
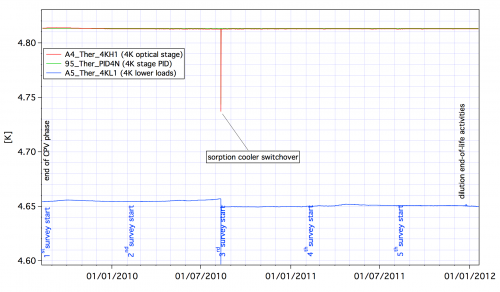
The 4K cooler was operated without interruption during all the survey phase of the mission. It is still in operation as it also provides the cooling of the optical reference loads of the LFI. The 4K PID stabilizing the temperature of the HFI optics is regulated at 4.81 K using a power around 1.8 mW.
The 4K J-T cooler compressors amplitude was set to 3450 micrometers during the CPV, and was maintained to this value during all the mission. Its cooling power is very stable and gives enough margin to cancel out the fluctuations induced by the sorption cooler fluctuations and adjustments. Following the unexpected shutdown of the compressors during CPV, their operation was nominal during all the rest of the mission.
Details on the in-flight performance of the 4K J-T cooler can be found in in section 5.3 of Planck early paper II .
Cold optics[edit]
(Lamarre)
Horns,lenses[edit]
links to Peter's paper
Feed horns beams (sub-system level)[edit]
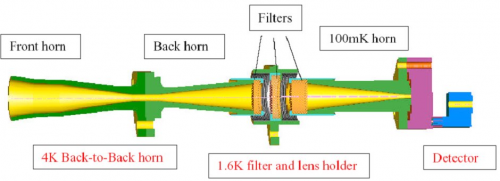
In order to meet with straylight, beam shapes and filtering requirements, a design using feedhorn coupled detectors has been chosen, with a triple horn configuration (see Figure 3.1.1). A detailed description of the HFI optical design and beam performances is given in Maffei et al.(2009) and Ade et al.(2009).
Single-moded horns patterns[edit]
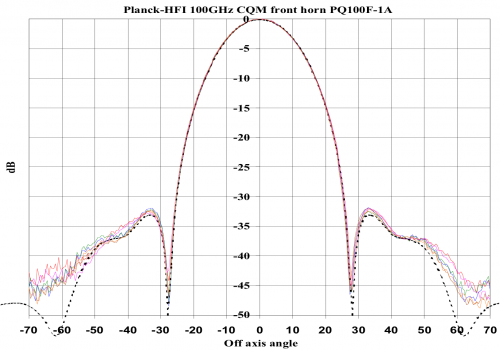
The spectral and geometrical properties of the horns have been characterized individually. The measured beam pattern of a typical front horn is compared with the prediction from the design (figure 3.1.2). The fit is excellent down to very low levels, which validates the logics that prevailed for characterizing the horns: modelling and optimizing the horns before implementation. Validating the model with a complete measurement of the beam intensity patterns.
For the single-moded horns, a method has been developed to use the measured intensities, together with the phase information from modeling to derive “worst-case” horn beam patterns that can be used in GRASP simulations of the telescope beams (phase information is mandatory). Worst-case beam patterns have been computed for all single-moded HFI horn types. A .pdf file (IAS-FN-WCB-001-03022009) detailing the algorithm can be found on the optics ftp site at ctwg1.planck.fr, in the following directory: /File_Exchange_Box_GOPT/Files_from_FN/Worst_case_beams”
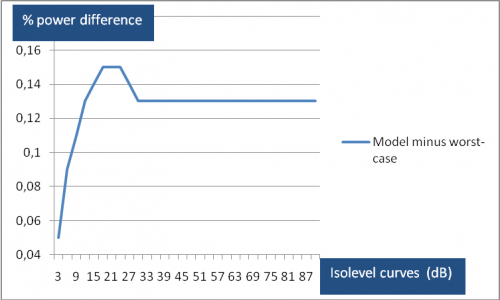
As an example, in Figure 3.1.3, we show the difference in encircled powers at constant isolevel intervals for the HFI 143_1a channel main beam using both the model and worst-case horns.
Ideal Multi-moded horns simulations[edit]
In the high frequency 545GHz and 857GHz Planck pixels both the back-to-back (BTB) horn and the detector horn have overmoded waveguide filters. The waveguide-horn structures are modelled using the scattering matrix approach used for the single-moded-CMB-channel horns, with the inclusion of modes of azimuthal orders, n = 0, 1, 2, 3 and 4. We assume reciprocity, and that the cavity plus cavity horn and filter behaves like a black-body: since the waveguide filter in the detector horn is wider than that of the BTB, it is reasonable to assume that any mode that can propagate through the BTB filter also propagates through the detector horn filter from the cavity. Thus, as far as the beam patterns are concerned the BTB is effectively coupled to a black body cavity also and all modes are excited at the back end of the BTB horn. Thus, all waveguide modes are equally excited in power but are also independent of each other so there is no phase relationship between them. Many of these modes may contribute independently (i.e. incoherently) to the beam on the sky. All coherent aperture fields have to be independently propagated through the PLANCK telescope.
From the S21 transmission scattering matrix for the whole BTB we recover the group of true independent hybrid fields that are transmitted by the waveguide filter and horn at the aperture of the BTB. These hybrid fields propagate independently through the telescope and onto the sky at a single frequency. The beam pattern for the band is obtained by adding the filter transmission weighted coherent fields in quadrature across the band (Microwave Horns and Feeds A. David Olver, Institution of Electrical Engineers) (“Shaped Corrugated horns for Cosmic Microwave Background Anisotropy Measurements” B. Maffei, P.A.R. Ade, C.E. Tucker, E. Wakui, R.J. Wylde, J.A. Murphy, R.M. Colgan, Int Jour Infrared & Millimeter waves, 21, (12) 2023-2033, December 2000).
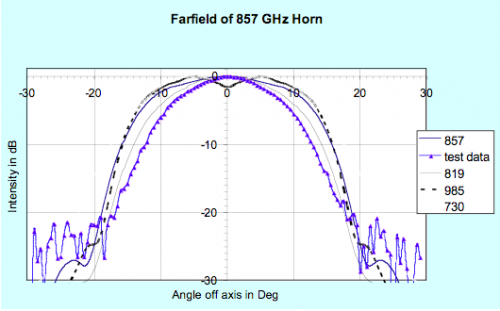
Far field patterns of horns and comparison with test data:
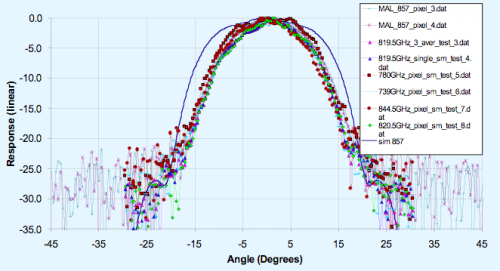
The far-field patterns of the horns (which illuminate the Planck mirrors) have been simulated and are shown in figure 3.1.4a for a few spot frequencies across the 857 GHz band. Note that the edge taper is approx -30dB at 25 degrees as required at the centre of the band. Superimposed is the broadband measurement made at Cardiff (see below) which clearly looks narrower than the majority of the spot frequency measurements and requires explanation. The measured far field beam patterns across the band are narrower than the predicted far field beams right across the band. The simulated beams are too wide suggesting missing higher order modes, either due to attenuation between the cavity and the BTB, or to the experimental setup. Away from the band centre the theoretical beams also appear to be too wide, indicating missing modes (see figure 3.1.4b).
Grouping contributions according to azimuthal order and overlaying the measurement data to investigate missing field distributions, modes of order 2 and higher appear to be absent. The beam containing modes of azimuthal orders n = 0 and 1 appears to fit the measured beams reasonably. Adding modes with azimuthal order n = 2 gives a simulated beam that is too wide, suggesting that these modes are absent from the measured BTB front aperture field.
Spectral Characterization of the HFI Detector Focal Plane[edit]
(Spencer) This section is comprised of excerpts from the HFI - Spectral Calibration report of the IAS measurements, v3.02, an internal report describing detailed pre-flight ground based measurements of the HFI focal plane. The experimental setup, data collection, and related data processing are described. The official version of the HFI detector spectral transmission profiles is available within the HFI instrument model and the RIMO files in the Planck Legacy archive [ref.] . This data is comprised of broadband Fourier transform spectrometer (FTS) measurements conducted with the HFI focal plane assembly in a ground-based test cryostat, and includes a waveguide model for the low frequency spectral region, and component-level filter spectra for the remaining out of band spectral regions. Specific attention is given to in-band and near-band spectral regions surrounding CO rotational transitions in order to support the CO extraction component separation effort [ref.] . The spectral transmission profiles are evaluated with parameters such as cut-on, cut-off, centre frequency, effective frequency (including spectral index), and band-width, all provided in this analysis. Further evaluation yields band-average spectra ( [ref.] ) and unit conversion / colour correction coefficients ( [ref.] ) and software routines to generate additional unit conversion and colour correction coefficients ( [ref.] ).
The main goal of the spectral transmission tests of the HFI instrument is to measure the spectral response of all HFI detectors to a known source of EM radiation individually. This was determined by measuring the interferometric output of all detection channels for radiation propagated through a continuously scanned polarising Fourier transform spectrometer (FTS). The required accuracy to which the spectral transmission is to be recovered is 1. It is important to note that the absolute spectral calibration cannot be achieved solely from the analysis of the FTS data because of uncertainties in the coupling efficiency of the FTS source through the FTS, input optics, and integrating sphere. The relative FTS measurements must be combined with the optical efficiency tests which used internal black-body sources (EFF Test – see §EFF). A reference bolometer located in an intermediate integrating sphere (accepting sr of incident radiation) within the FTS test setup was used to ratio the HFI detector spectra against to determine the throughput-normalized relative transmission spectra for each HFI detector. Data were collected over a series of pre-flight test campaigns, and processed/analyzed using standard Fourier data processing techniques.
Additional Experiments[edit]
There were two significant additional tests that are used in the derivation of the HFI detector spectral transmission profiles beyond the scope of the IAS HFI FTS measurements. Additional filter measurements were recorded in the Astronomical Instrumentation Group (AIG) test facility at Cardiff during filter stack production. These measurements are used to extend the IAS FTS spectral measurements beyond the HFI spectral passband. The EFF tests are used to obtain optical efficiency parameters for each detector. These parameters, when combined with the respective normalized spectral transmission profiles, provide an estimate of the absolute spectral transmission. The EFF tests are discussed in greater detail by A. Catalano ( [ref.] ). The filter measurements are described in §filter below.
Filter Measurements[edit]
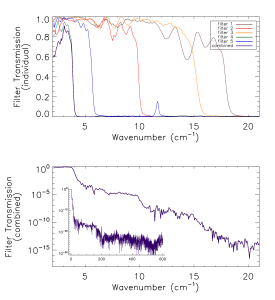
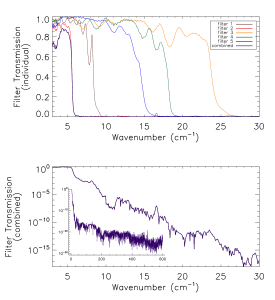
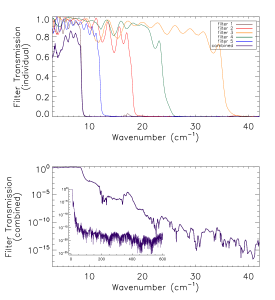
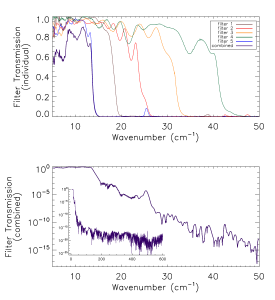
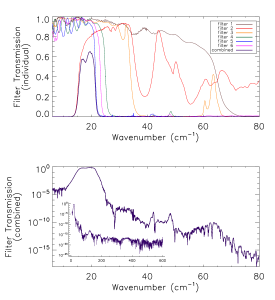
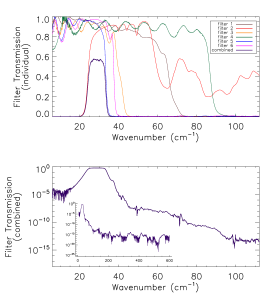
Prior to the IAS measurements with the integrated HFI detectors and filter stacks, FTS measurements of the individual filters comprising the filter stacks for each band were conducted at Cardiff. As will be discussed in §[sec:OOB], the independent measure of the filter stack transmission is used for a portion of the HFI detector spectral transmission for regions of the spectrum where it is deemed to be of better quality than the IAS FTS measurements (i.e. for frequencies outside of the band edge filter cut-off(s)). The filter stacks for each of the frequency bands are comprised of 5 filters. There is an additional low frequency cut-on filter for the 545 and 857 GHz bands as the waveguide cut-on is too low for these multi-moded channels. Figures [fig:Filt100] – [fig:Filt857] show the individual filter transmission measurements as well as the combined filter stack product.
- Combined (bottom) and individual (top) filter transmission measurements for the 5 filters within the HFI band filter stacks (6 for 545 and 857 GHz).
The uncertainty on the combined filter transmission measurement is determined as follows. Let represent the individual filter transmission. The standard deviation of all values of below a threshold of is used as an approximate uncertainty for each individual filter measurement, i.e. . The individual uncertainty estimates are combined to provide an estimate of the combined filter transmission spectral uncertainty through standard error propagation. For the combined filter transmission represented as , the associated uncertainty estimate is given as
Data Processing and Fourier Transformation[edit]
<1-- [sec:DP] -->
Having identified the data sections that are of interest, here follows the data processing sequence used to obtain the resulting spectra. The processing steps taken are as follows:
- Selection and extraction of time sampled data sets
- Conversion of time sampled data to arrays of OPD sampled interferogram data sets
- Fourier transformation and averaging of interferogram data sets
- Discrimination of poor quality spectra by standard deviation comparison (see §[sec:FTavg])
- Division of detector spectra by reference bolometer spectra to obtain normalized spectral transmission profiles
- Combination of relative transmission spectra with filter measurements and waveguide models
- Determination of optical efficiency through evaluation of normalized spectral transmission in the context of the EFF experiments
- Addition of over-sampled data into spectrum for the CO transition regions (see §[sec:CO])
- Identification of common frequency sampling per channel and interpolation of spectra onto the common sampling
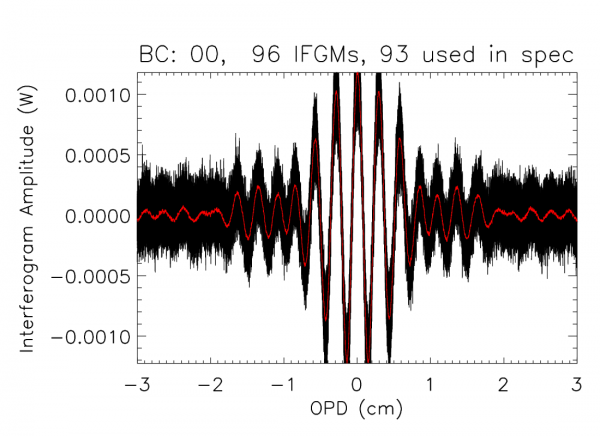
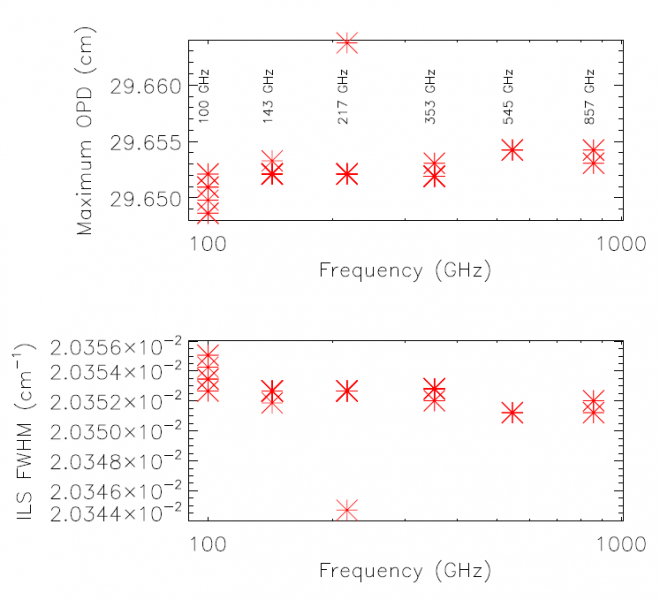
The bolometer signal is stored within the initial database in several formats: raw ADU, signal voltage, resistance, current, temperature, total power, electrical power, and radiant power, all of which may be exported as a function of sample time. A bolometer model was applied to the raw data to produce interferograms in units of absorbed optical power. This both reduced the in-band effects of detector nonlinearities, and allowed another comparison of optical efficiency to complement the EFF tests. The location of Zero Optical Path Difference (ZPD) is estimated for each interferogram, and the interferogram boundaries are determined as the mid-points between subsequent interferograms, less a small number of buffer points (10) to ensure that the extracted interferograms include regions associated with the FTS stage travel having constant velocity while excluding the acceleration regions. Visual verification of the extracted interferograms is performed prior to subsequent processing and averaging to ensure that each ZPD was identified correctly, and to remove any low-quality interferograms. The overlap of the extracted interferograms is also verified visually. Once interferograms have been extracted from each data set, the overall spectral resolution is evaluated and an evenly sampled Optical Path Difference (OPD) grid onto which each interferogram in the combined data is then interpolated is generated. This ensures that each individual interferogram is sampled at ZPD and that each spectrum has identical frequency sampling and can thus be averaged together. An example of a combined interferogram data set is illustrated in Figure [fig:CombinedIFGMex] where the central portions of the recorded interferograms are shown. A similar plot for each HFI detector is included in the Appendices (see §[sec:allIFGMs]). The MPD value for each detector, and corresponding spectral resolution, is shown in Fig. [fig:MPD].
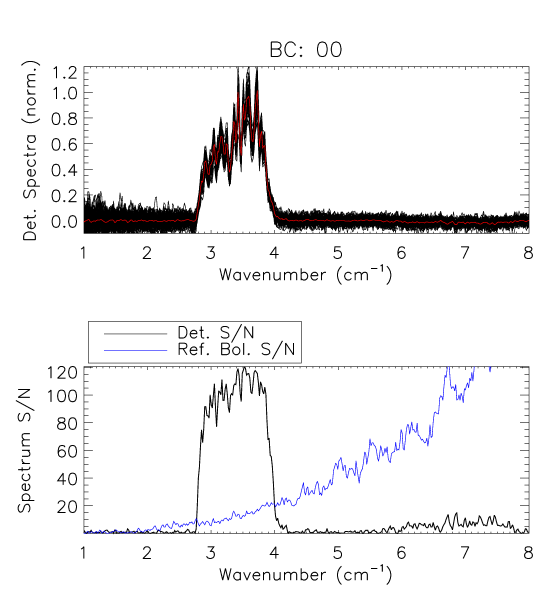
In preparation for Fourier transformation, a low-order polynomial baseline removal is performed on the individual interferograms. Consequently, no information can be recovered from the spectrum below , but this is of no concern as this region of the spectrum is replaced by a waveguide fit in the final data product (see §[sec:WG]). An average interferogram is determined and used to identify glitches for removal from the interferogram data. Following glitch removal, individual interferograms undergo standard Fourier data processing. The modified Norton-Beer 1.5 apodization function ( [ref.] ) has been selected to be used for the final spectral transmission profile data set as it represents a good compromise between the desired ILS sidelobe reduction and improved S/N with marginal reduction in spectral resolution. Data averaging is then performed in the spectral domain. The uncertainty for every spectral data point is determined statistically through the standard deviation at a given frequency. A check for poor quality spectra is performed by comparing the overall standard deviation including and excluding any given spectrum. An example of the individual spectra and uncertainty for bc00 is shown in Fig. [fig:CombinedSpecEx], along with the corresponding S/N of the reference bolometer spectrum; similar plots for all of the detectors are shown in §[sec:allSpecs]. An estimate of the spectral S/N for each detector is obtained using the average spectrum and its statistical uncertainty, averaged across the in-band region of the spectrum. The averaged spectra are then normalized and divided by a (normalized) reference bolometer spectrum (see §[sec:setup] & §[sec:Bref]) to obtain the HFI detector relative spectral response.
| Band (GHz) | bc | # Ifgm. | # Spec. | MPD (cm) | ILS (cm) | avg. S/N |
| 100 | 00 | 96 | 93 | 29.648639 | 0.020355066 | 104.70555 |
| 100 | 01 | 96 | 95 | 29.648639 | 0.020355066 | 203.34226 |
| 100 | 20 | 96 | 96 | 29.649801 | 0.020354268 | 271.38262 |
| 100 | 21 | 95 | 94 | 29.650962 | 0.020353471 | 264.65385 |
| 100 | 40 | 96 | 94 | 29.652124 | 0.020352674 | 432.40921 |
| 100 | 41 | 96 | 96 | 29.652124 | 0.020352674 | 962.98064 |
| 100 | 80 | 95 | 95 | 29.650962 | 0.020353471 | 262.71036 |
| 100 | 81 | 96 | 96 | 29.650962 | 0.020353471 | 227.35782 |
| 143 | 02 | 96 | 95 | 29.652124 | 0.020352674 | 434.93136 |
| 143 | 03 | 96 | 96 | 29.652124 | 0.020352674 | 458.86741 |
| 143 | 10 | 95 | 95 | 29.652124 | 0.020352674 | 565.21311 |
| 143 | 30 | 92 | 92 | 29.653286 | 0.020351876 | 424.53824 |
| 143 | 31 | 92 | 92 | 29.652124 | 0.020352674 | 447.50343 |
| 143 | 42 | 92 | 92 | 29.652124 | 0.020352674 | 536.23423 |
| 143 | 50 | 96 | 96 | 29.652124 | 0.020352674 | 441.68983 |
| 143 | 51 | 96 | 96 | 29.652124 | 0.020352674 | 476.22684 |
| 143 | 60 | 96 | 96 | 29.652124 | 0.020352674 | 517.43269 |
| 143 | 70 | 95 | 94 | 29.652124 | 0.020352674 | 326.06542 |
| 143 | 82 | 96 | 96 | 29.652124 | 0.020352674 | 454.23293 |
| 143 | 83 | 96 | 96 | 29.652124 | 0.020352674 | 439.50612 |
| 217 | 04 | 96 | 96 | 29.652124 | 0.020352674 | 625.92713 |
| 217 | 11 | 96 | 96 | 29.652124 | 0.020352674 | 580.32904 |
| 217 | 12 | 67 | 67 | 29.663741 | 0.020344703 | 549.24264 |
| 217 | 22 | 96 | 96 | 29.652124 | 0.020352674 | 550.65242 |
| 217 | 43 | 95 | 95 | 29.652124 | 0.020352674 | 616.57750 |
| 217 | 44 | 96 | 96 | 29.652124 | 0.020352674 | 543.78288 |
| 217 | 52 | 95 | 94 | 29.652124 | 0.020352674 | 684.91039 |
| 217 | 61 | 92 | 92 | 29.652124 | 0.020352674 | 594.70296 |
| 217 | 62 | 95 | 95 | 29.652124 | 0.020352674 | 579.69385 |
| 217 | 71 | 96 | 96 | 29.652124 | 0.020352674 | 631.30065 |
| 217 | 72 | 96 | 96 | 29.652124 | 0.020352674 | 687.10844 |
| 217 | 84 | 92 | 92 | 29.652124 | 0.020352674 | 636.36790 |
| 353 | 05 | 55 | 55 | 29.651916 | 0.020352816 | 354.15815 |
| 353 | 13 | 57 | 57 | 29.651916 | 0.020352816 | 319.09858 |
| 353 | 23 | 55 | 55 | 29.651916 | 0.020352816 | 218.05772 |
| 353 | 24 | 64 | 64 | 29.651916 | 0.020352816 | 236.44464 |
| 353 | 32 | 56 | 56 | 29.651916 | 0.020352816 | 238.40018 |
| 353 | 33 | 55 | 55 | 29.651916 | 0.020352816 | 219.60443 |
| 353 | 45 | 64 | 64 | 29.653078 | 0.020352019 | 246.97889 |
| 353 | 53 | 57 | 57 | 29.651916 | 0.020352816 | 225.27621 |
| 353 | 54 | 57 | 57 | 29.651916 | 0.020352816 | 228.47058 |
| 353 | 63 | 57 | 56 | 29.651916 | 0.020352816 | 140.16991 |
| 353 | 64 | 55 | 55 | 29.651916 | 0.020352816 | 158.85037 |
| 353 | 85 | 57 | 57 | 29.653078 | 0.020352019 | 246.18460 |
| 545 | 14 | 63 | 63 | 29.654240 | 0.020351221 | 448.67624 |
| 545 | 34 | 64 | 64 | 29.654240 | 0.020351221 | 481.87111 |
| 545 | 55 | 57 | 57 | 29.654240 | 0.020351221 | 328.07835 |
| 545 | 73 | 57 | 57 | 29.654240 | 0.020351221 | 447.49901 |
| 857 | 25 | 64 | 64 | 29.653078 | 0.020352019 | 501.25106 |
| 857 | 35 | 64 | 64 | 29.654240 | 0.020351221 | 567.55125 |
| 857 | 65 | 42 | 42 | 29.653078 | 0.020352019 | 482.41906 |
| 857 | 74 | 64 | 64 | 29.654240 | 0.020351221 | 491.89133 |
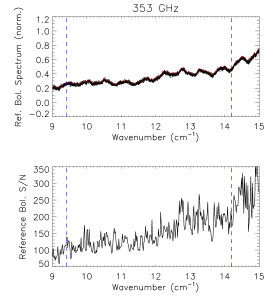
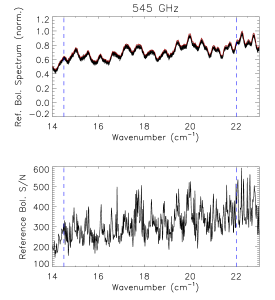
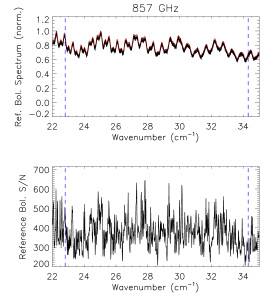
Reference Bolometer Spectra[edit]
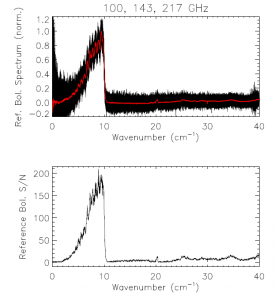
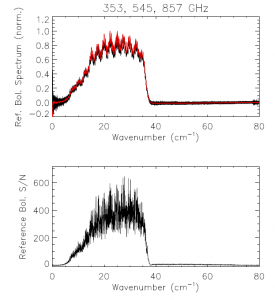
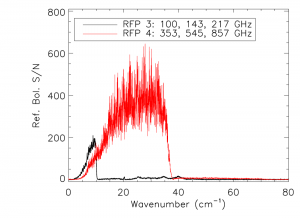
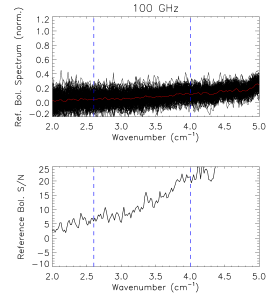
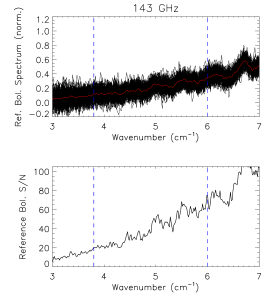
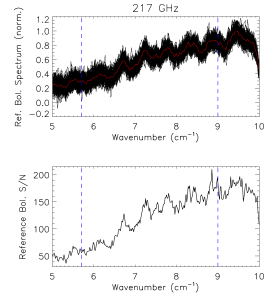
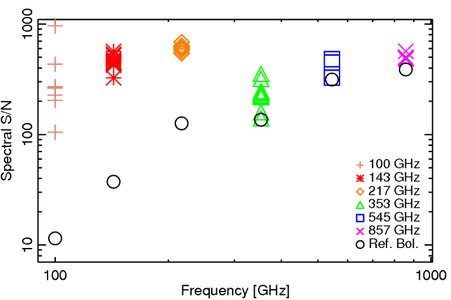
The reference bolometer spectra are obtained in a fashion similar to that used for the HFI detectors. Wherever possible, the same data processing is applied to the reference bolometer data as was applied to the HFI detector data, including optical filtering, scan speed, scan length, source intensity, apodization, phase correction, etc. Table [tab:Brefstats] contains the reference bolometer data set properties corresponding those listed for the HFI detectors in Table [tab:Igstats]. Figures [fig:BrefL] - [fig:Bref857] illustrate the resultant spectra and S/N from the reference bolometer data sets. Figure [fig:SNall] compares the approximate S/N of the average spectrum for each detector against the reference bolometer average spectrum S/N over the same spectral region.
| Band (GHz) | # Ifgm. | # Spec. | MPD (cm) | ILS (cm) | avg. S/N |
| 100 | 164 | 164 | 29.644698 | 0.020357772 | 11.478057 |
| 143 | 164 | 164 | 29.644698 | 0.020357772 | 37.361317 |
| 217 | 164 | 164 | 29.644698 | 0.020357772 | 126.14280 |
| 353 | 24 | 24 | 29.652306 | 0.020352549 | 136.06159 |
| 545 | 24 | 24 | 29.652306 | 0.020352549 | 314.58093 |
| 857 | 24 | 24 | 29.652306 | 0.020352549 | 388.23050 |
- Reference bolometer spectra and S/N.
- Reference bolometer spectra (top) and S/N (bottom) for each of the HFI bands (vertical bars represent band edges).
Out-of-Band Spectral Transmission Content[edit]
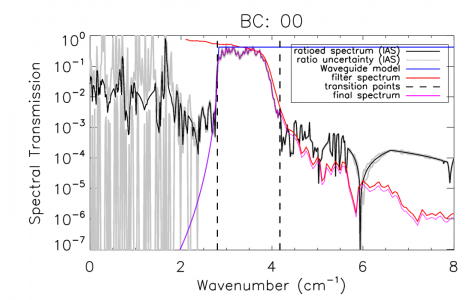
The HFI detector spectral transmission profiles have been extended beyond the optical pass-band of the detectors. This is done by using a combination of a waveguide model and external filter measurements for the out-of-band regions of the detector spectral response. An uncertainty estimate for these additional spectral regions is also provided, however, it should be noted that the spectral uncertainty for the waveguide and filter spectra are determined indirectly (as described above/below). There is a transition from IAS FTS data to filter data for every band edge which is defined by an optical filter. For the 100, 143, 217, and 353 GHz bands this is the high frequency cut-off band edge. For the 545 and 857 GHz bands a separate filter is used to define each of the high and low frequency band edges. For the spectral regions outside of the HFI detector optical bands, first the IAS FTS data is used to qualitatively verify that there are no spectral leaks or features, and then the external filter measurements are grafted into the ratioed spectra where they better represent the relative spectral transmission.
The normalized ratioed spectrum and filter are both scaled by the optical efficiency (see §[sec:EFF]). For the 100 - 353 bands, the filter spectrum is also scaled by to account for single-moded throughput normalization. This frequency scaling results in a more accurate in- and near-band match between the two sets of spectra, at the cost of less accuracy at much higher frequencies where any transmission will not be single-moded. As ransmission at higher frequencies is significantly reduced, this trade-off is acceptable. The 545 and 857 GHz bands have their filter spectra without the additional frequency scaling as this is not correct for multi-moded propagation. Both lower and upper frequency thresholds, , and , are defined for each band, below and above which the IAS-FTS spectra and/or the Cardiff composite filter spectra must be used, respectively. This is done to avoid introducing any detector nonlinearity residuals into the final spectral transmission data products. The region between these two points is defined as the transition region; within this region the amplitudes and slopes of the IAS and filter spectra are used to determine the spectral cross-oveer/transition point. Additional checks are performed to ensure that non-physical data processing artefacts are not introduced into the spectral transition region. Additionally, a similar technique is used, with decreasing frequency instead of increasing, for the 545 and 857 GHz bands with a filter-induced frequency cut-on. Figure [fig:OOBex] illustrates an example of both the FTS and filter spectra used in extending the transmission profiles beyond the HFI optical bands. Similar plots for every detector are shown in §[sec:stitch].
Waveguide Model[edit]
A waveguide model is used to provide the data for the lowest frequency portion of the HFI detector spectral transmission. For the 100, 143, 217, and 353 GHz bands the waveguide model is transitioned (with increasing frequency) to the FTS ratioed spectra directly. There is an intermediate transition to the filter data, and then the ratioed spectra for the 545 and 857 GHz bands. For each detector, the waveguide transmission, , is given by the following relation
where is the frequency in cm, is the waveguide radius in cm, is the waveguide length in cm, and is a waveguide specific constant; 1.841 for the TE/TM (HE) hybrid mode in this case . Table [tab:WG] lists the waveguide radii and lengths resultant from the waveguide model fit to the ratioed spectra. As all of the feedhorns for a given band are meant to be identical (i.e. within mechanical manufacturing tolerances) the uncertainty of the waveguide transmission is estimated statistically using all of the waveguide models for each band. I.e. for bands, the uncertainty at each spectral data point is determined by the standard deviation of transmission values at that frequency. As a result of each detector in a given band having a unique cut-on frequency, this method begins to over-estimate the uncertainty for frequencies approaching the cut-on; for regions very near the waveguide cut-on, the uncertainty is extrapolated from the ratioed spectrum as a more accurate representation.
| Band (GHz) | bc | Det. | r (mm) | r (mm) |
| 100 | 00 | 1a | 1.039705 | 1000 |
| 100 | 01 | 1b | 1.038040 | 12.5813 |
| 100 | 20 | 2a | 1.038375 | 14.3000 |
| 100 | 21 | 2b | 1.041035 | 12.3750 |
| 100 | 40 | 3a | 1.042370 | 12.9250 |
| 100 | 41 | 3b | 1.042370 | 12.5125 |
| 100 | 80 | 4a | 1.033050 | 13.2000 |
| 100 | 81 | 4b | 1.033050 | 12.6500 |
| 143 | 02 | 1a | 0.740345 | 9.4500 |
| 143 | 03 | 1b | 0.737550 | 9.5625 |
| 143 | 10 | 5 | 0.736155 | 9.4500 |
| 143 | 30 | 2a | 0.740345 | 9.4500 |
| 143 | 31 | 2b | 0.739880 | 9.2250 |
| 143 | 42 | 6 | 0.741275 | 9.4500 |
| 143 | 50 | 3a | 0.741275 | 9.4500 |
| 143 | 51 | 3b | 0.741275 | 9.4500 |
| 143 | 60 | 7 | 0.729635 | 9.7875 |
| 143 | 70 | 8 | 0.739415 | 9.4500 |
| 143 | 82 | 4a | 0.739415 | 9.4500 |
| 143 | 83 | 4b | 0.738480 | 9.4500 |
| 217 | 04 | 1 | 0.4740750 | 7.8000 |
| 217 | 11 | 5a | 0.4814250 | 7.8000 |
| 217 | 12 | 5b | 0.4817310 | 8.0000 |
| 217 | 22 | 2 | 0.4749935 | 7.8000 |
| 217 | 43 | 6a | 0.4832625 | 8.0000 |
| 217 | 44 | 6b | 0.4832625 | 8.0000 |
| 217 | 52 | 3 | 0.4753000 | 8.0000 |
| 217 | 61 | 7a | 0.4820375 | 8.0000 |
| 217 | 62 | 7b | 0.4820375 | 8.0000 |
| 217 | 71 | 8a | 0.4838750 | 8.0000 |
| 217 | 72 | 8b | 0.4838750 | 1000 |
| 217 | 84 | 4 | 0.4740750 | 7.6000 |
| 353 | 05 | 1 | 0.2921850 | 6.47500 |
| 353 | 13 | 2 | 14300 | 7.00000 |
| 353 | 23 | 3a | 0.2891650 | 7.70000 |
| 353 | 24 | 3b | 3535 | 7.52500 |
| 353 | 32 | 4a | 0.2869000 | 7.35000 |
| 353 | 33 | 4b | 0.2870890 | 7.39375 |
| 353 | 45 | 7 | 0.2876550 | 6.12500 |
| 353 | 53 | 5a | 0.2936950 | 7.35000 |
| 353 | 54 | 5b | 0.2936950 | 7.61250 |
| 353 | 63 | 6a | 0.2929400 | 6.73750 |
| 353 | 64 | 6b | 0.2925625 | 6.62500 |
| 353 | 85 | 8 | 0.2889765 | 6.73750 |
| 545 | 14 | 1 | 1000 | 3.600 |
| 545 | 34 | 2 | 0.3865875 | 3.525 |
| 545 | 55 | 3 | 0.3800065 | 3.525 |
| 545 | 73 | 4 | 0.3787875 | 3.525 |
| 857 | 25 | 1 | 0.2985 | 2.4 |
| 857 | 35 | 2 | 0.2985 | 2.4 |
| 857 | 65 | 3 | 0.2985 | 2.4 |
| 857 | 74 | 4 | 0.2985 | 2.4 |
Optical Efficiency[edit]
The EFF tests involved exposing the HFI detectors to a known blackbody source and observing the response. Sufficient details for the HFI detector spectral transmission profiles are provided here while full details of the EFF experiments and results are provided in a separate technical report . A blackbody source internal to the Saturne cryostat was set to a variety of temperatures (1 – 6 K) and the bolometer detector response was recorded. A bolometer model was applied to the recorded response in order to obtain the radiative optical power absorbed by the detector, in units of W, i.e. where represents the blackbody source temperature. Using the measured source temperature, the theoretical radiative optical power incident on the detector is also calculated using the Planck function. The ratio of the received power and the theoretical power provides the optical efficiency term. To remove any offsets in the measurement, a ratio of differences between unique temperature settings is used. The measured absorbed optical power difference is given by
where and represent two unique source temperature settings. The theoretical incident power is determined using the HFI detector spectral transmission profiles. Let represent the normalized detector transmission spectrum (i.e. it has been ratioed and had the waveguide model and filter data appropriately grafted). The spectral transmission is scaled for throughput and then re-normalized as follows
where is the division of by its maximum value, and is the speed of light. The normalized spectral transmission is then used with the Planck function at the temperature setting to determine the theoretical power, , as follows
where is the Planck constant, is the Boltzmann constant, the integration limits are given by and , and is the expected mode content of the frequency band. Table [tab:modes] lists the values used for each band . In this case the integration is performed over the range . The difference between the theoretical power loading is given by
which allows the optical efficiency term to be determined as follows
Thus, if were used in Equation [eq:EFFPth] in place of , the resultant optical efficiency would be unity, indicating that the transmission losses have already been taken into account.
The uncertainty estimate of the optical efficiency is statistically based on the results from the multiple temperature settings used in the EFF test sequences.
| Band (GHz) | 100 | 143 | 217 | 353 | 545 | 857 |
| 1 | 1 | 1 | 1 | 3.4 | 8.3 |
CO interpolation[edit]
The IAS FTS/Saturne data taken with the HFI detectors is limited to a spectral resolution of by the mechanical travel of the FTS translation stage. This corresponds to an unapodized FTS ILS FWHM of . The previous iteration of the spectral transmission (IMO ver. 2_28), in addition to a triangular apodization kernel, has a factor of 3 sub-sampled spectral resolution to improve the signal-to-noise ratio (S/N) of the output spectra. In light of the CO contribution to the 100 GHz spectra, the spectral transmission has been reprocessed at the original full spectral resolution with a different apodization function which provides better noise reduction and less spectral resolution degradation, as discussed above.
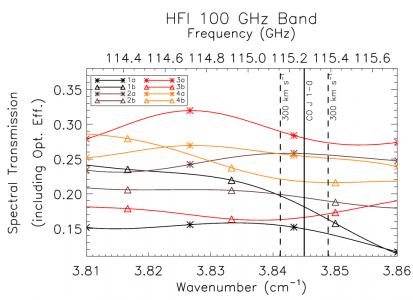
In order to provide an improved estimate of the spectral transmission near the CO features, an interpolation of the spectra by a factor of 10 has been performed. This over-sampling was accomplished by zero-padding the FTS interferograms prior to Fourier transformation , and subsequently incorporated into the Nyquist-sampled spectral data near the CO transitions (see Table [tab:CO]). Although the data are presented at higher resolution, the resolution of independent data points is not improved, i.e. the ILS line-width remains the same. A flag column has been added to the spectral transmission profile data files to indicate whether a given data point originates from the actual data, or is a result of the ILS-based interpolation. The region of the over-sampled, interpolated, data has been extended to also include other CO isotopes; the COJ1-0 – J9-8 transitions should be oversampled for CO, CO, CO, and CO. The original data points within the over-sampled region have been preserved (i.e. every tenth data point – the data point that is not an interpolated one – is flagged with a zero rather than a one), as is indicated by the data flag, so a flag filter on the data will restore the independent data points easily. Figure [fig:COflag] illustrates the regions where the over-sampling has been incorporated into the spectral transmission profiles. An example of the over-sampled spectra is shown in Figure [fig:COzoom100] for the 100 GHz detectors. Examples for the other detector bands are shown in §[sec:COappend]
| Band (GHz) | CO transition ( - ) | (GHz) | over-sampled region (GHz) |
| 100 | 1 – 0 | 115.2712018 | 109.67 – 115.39 |
| 143 | 1 – 0 | 115.2712018 | 109.67 – 115.39 |
| 143 | 2 – 1 | 230.5380000 | 219.34 – 230.77 |
| 217 | 2 – 1 | 230.5380000 | 219.34 – 230.77 |
| 353 | 3 – 2 | 345.7959899 | 329.00 – 346.15 |
| 545 | 4 – 3 | 461.0407682 | 438.64 – 461.51 |
| 545 | 5 – 4 | 576.2679305 | 548.28 – 576.85 |
| 857 | 6 – 5 | 691.4730763 | 657.89 – 692.17 |
| 857 | 7 – 6 | 806.6518060 | 767.48 – 807.46 |
| 857 | 8 – 7 | 921.7997000 | 877.04 – 922.73 |
| 857 | 9 – 8 | 1036.9123930 | 986.57 – 1037.95 |
| BC | Det. | CO transition () | Transmission | |
| 100 | 00 | 1a | 1 – 0 | 0.1495 0.0054 |
| 100 | 01 | 1b | 1 – 0 | 0.1812 0.0052 |
| 100 | 20 | 2a | 1 – 0 | 0.2577 0.0119 |
| 100 | 21 | 2b | 1 – 0 | 0.1944 0.0086 |
| 100 | 40 | 3a | 1 – 0 | 0.2798 0.0133 |
| 100 | 41 | 3b | 1 – 0 | 0.1660 0.0093 |
| 100 | 80 | 4a | 1 – 0 | 0.2538 0.0114 |
| 100 | 81 | 4b | 1 – 0 | 2173 0.0105 |
| 217 | 04 | 1 | 2 – 1 | 0.3781 0.0026 |
| 217 | 11 | 5a | 2 – 1 | 0.4530 0.0029 |
| 217 | 12 | 5b | 2 – 1 | 0.4174 0.0030 |
| 217 | 22 | 2 | 2 – 1 | 0.3773 0.0026 |
| 217 | 43 | 6a | 2 – 1 | 0.3149 0.0023 |
| 217 | 44 | 6b | 2 – 1 | 0.3609 0.0030 |
| 217 | 52 | 3 | 2 – 1 | 0.3924 0.0025 |
| 217 | 61 | 7a | 2 – 1 | 0.3428 0.0022 |
| 217 | 62 | 7b | 2 – 1 | 0.2770 0.0017 |
| 217 | 71 | 8a | 2 – 1 | 0.4623 0.0031 |
| 217 | 72 | 8b | 2 – 1 | 0.4340 0.0031 |
| 217 | 84 | 4 | 2 – 1 | 0.3506 0.0025 |
| 353 | 13 | 2 | 3 – 2 | 0.5461 0.0044 |
| 353 | 23 | 3a | 3 – 2 | 0.3443 0.0030 |
| 353 | 24 | 3b | 3 – 2 | 0.4706 0.0037 |
| 353 | 32 | 4a | 3 – 2 | 0.3099 0.0024 |
| 353 | 33 | 4b | 3 – 2 | 0.2801 0.0027 |
| 353 | 45 | 7 | 3 – 2 | 0.2923 0.0022 |
| 353 | 53 | 5a | 3 – 2 | 0.3150 0.0024 |
| 353 | 54 | 5b | 3 – 2 | 0.3181 0.0023 |
| 353 | 63 | 6a | 3 – 2 | 0.2059 0.0014 |
| 353 | 64 | 6b | 3 – 2 | 0.2113 0.0017 |
| 353 | 85 | 8 | 3 – 2 | 0.3509 0.0028 |
| 545 | 14 | 1 | 4 – 3 | 0.0747 0.0003 |
| 545 | 34 | 2 | 4 – 3 | 0.0731 0.0003 |
| 545 | 55 | 3 | 4 – 3 | 0.0521 0.0002 |
| 545 | 73 | 4 | 4 – 3 | 0.0473 0.0002 |
| 545 | 14 | 1 | 5 – 4 | 0.3306 0.0012 |
| 545 | 34 | 2 | 5 – 4 | 0.3183 0.0011 |
| 545 | 55 | 3 | 5 – 4 | 0.2428 0.0009 |
| 545 | 73 | 4 | 5 – 4 | 0.2597 0.0009 |
| 857 | 25 | 1 | 6 – 5 | 0.0280 0.0001 |
| 857 | 35 | 2 | 6 – 5 | 0.0241 0.0001 |
| 857 | 65 | 3 | 6 – 5 | 0.0292 0.0001 |
| 857 | 74 | 4 | 6 – 5 | 0.0159 0.0001 |
| 857 | 25 | 1 | 7 – 6 | 0.1636 0.0005 |
| 857 | 35 | 2 | 7 – 6 | 0.1427 0.0004 |
| 857 | 65 | 3 | 7 – 6 | 2176 0.0007 |
| 857 | 74 | 4 | 7 – 6 | 0.1168 0.0003 |
| 857 | 25 | 1 | 8 – 7 | 0.2554 0.0009 |
| 857 | 35 | 2 | 8 – 7 | 0.2218 0.0007 |
| 857 | 65 | 3 | 8 – 7 | 0.2744 0.0009 |
| 857 | 74 | 4 | 8 – 7 | 0.1119 0.0004 |
| 857 | 25 | 1 | 9 – 8 | 0.0053 0.0000 |
| 857 | 35 | 2 | 9 – 8 | 0.0060 0.0000 |
| 857 | 65 | 3 | 9 – 8 | 0.0085 0.0000 |
| 857 | 74 | 4 | 9 – 8 | 0.0001 0.0000 |
Spectral Response Conclusions and Conformity With Requirements[edit]
The two defining requirements indicated in the HFI calibration plan are the acquisition of the spectral transmission of the single pixels with a prescribed accuracy and spectral resolution. The desired accuracy is 3% for the low frequency channels (CMB – 100, 143, and 217 GHz) and 1% for the high frequency channels (353, 545, 857 GHz). The spectral resolution requirement is for a resolution superior to 0.1 cm.
The spectral resolution requirement has been exceeded by more than a factor of five. It is also possible to degrade the spectral resolution to the 0.1 cm requirement to gain an improvement in the S/N.
No quantitative number is present on the document regarding the blocking of high frequency (near IR, visible, UV) radiation outside the range of the instrument. Checks in order to quantify the rejection have been performed at subsystem level and estimates of the out-of-band transmission profiles have been incorporated into the data products. The high level of out-of-band signal attenuation is verified by in-flight observations as demonstrated in the Spectral Response paper ([ref.]).
Considering statistical fluctuations in the determination of the spectra, these goals have been achieved. There are, however, caveats regarding the nature of error bars when dealing with frequency space. The nature of uncertainties in spectra determination is less obvious than when dealing with timestream data. Systematic effects produced from instrumental setup, but also by data reduction can in some cases exceed the actual statistical oscillation in the determination of the final spectra. This is the case for the high-frequency data for instance where the statistical fluctuation of the different determinations of the spectra in some case are better than 1 part in .
A second caveat regards the method of data analysis of the calibration test data, for which the ratio with the reference bolometer data (of which the relative error is a function of frequency) introduces an error that increase with wavelength. With the spectral resolution of the data provided being much higher than the stated 0.1 cm, the transmission accuracy requirement is not met for the 100 GHz detectors. It is possible to degrade the spectral resolution to the 0.1cm level to allow the accuracy to achieve the required level, but the higher spectral resolution data has been provided to better assist with the CO contamination removal from the 100 GHz signal.
Figures containing the full spectral response of each HFI detector, and band-average spectra, are provided in the Appendix [ref.]. Details of the generation of band-average spectra, unit conversion coefficients, and colour correction coefficients are provided in the Data Processing sections of the Explanatory Supplement. IDL scripts have been provided alongside the PLA to allow users to generate unit conversion and colour correction coefficients; these are described in the PLA section [ref.].
Detection chain[edit]
(Francesco Piacentini)
Bolometers[edit]
The heart of the HFI - the detectors - are bolometers, solid-state devices in which the incoming radiation dissipates its energy as heat that increases the temperature of a thermometer. The instrument Flight Model total number of bolometers is 52, split into 6 channels at central frequencies of 100, 143, 217, 353, 545, and 857GHz. Two extra bolometers not optically coupled to the telescope are added to the focal plane to monitor thermal noise (Dark Bolometers).
Thirty two of these bolometers are polarization sensitive allowing a map of the CMB polarisation to be built.
Bolometers consist of (i) an absorber that transforms the in-coming radiation into heat; (ii) a thermometer that is thermally linked to the absorber and measures the temperature changes; and (iii) a weak thermal link to a thermal sink, to which the bolometer is attached.
The detectors are semi-conducting NTD thermistor bolometers. There are two kinds of detector modules:
- SWB, spider web bolometers, are mounted on an absorbing spider-web of metallised silicon nitride
- PSB, polarization sensitive bolometers, are mounted or on a parallel absorbing grid of metallised silicon nitride.
In the spider-web bolometers, or SWBs (Bock et al. 1995; Mauskopf et al. 1997), the absorbers consist of metallic grids
deposited on a Si3 N4 substrate in the shape of a spider web.
The mesh design and the impedance of the metallic layer are
adjusted to match vacuum impedance and maximize the absorption of millimeter waves, while minimizing the cross section to
particles. The absorber is designed to offer equal impedance to
any linearly polarised radiation. Nevertheless, the thermometer
and its electrical leads define a privileged orientation (Fig. SWB) that
makes the SWBs slightly sensitive to polarisation, as detailed in
(Rosset et al. 2010). The thermometers are
made of neutron transmuted doped (NTD) germanium (Haller
et al. 1996), chosen to have an impedance of about 10 MΩ at
their operating temperature.
The absorber of PSBs is a rectangular grid (Fig. PSB) with metallization in one direction (Jones et al.
2003). Electrical fields parallel to this direction develop currents and then deposit some power in the grid, while perpendicular electrical fields propagate through the grid without significant interaction. A second PSB perpendicular to the first one absorbs the other polarisation. Such a PSB pair measures two polarisations of radiation collected by the same horns and filtered by the same devices, which minimises the systematic effects: differences between polarised
beams collected by a given horn are typically less than −30 dB of
the peak. The differences in the spectral responses of a PSB pair
also proved to be a few percent in the worst case. Each pair
of PSBs sharing the same horn is able to measure the intensity
Stokes parameter and the Q parameter associated with its local
frame. An associated pair of PSBs rotated by 45◦ scans exactly
the same line (if the geometrical alignment is perfect), providing
the U Stokes parameter.
The detectors operate at a temperature close to 100 mK, while the filters are distributed on the 100mK, 1.6 K,
and 4 K stages in such a way that the heat load on the coldest stages is minimized to
limit the heat load on the detectors and to decrease
the heat lift requirement and thus enhance the mission lifetime. The self-emission of the 4K stage is minimised to limit the photon noise contribution on the detectors from the instrument.
The HFI Focal Plane Unit accommodates sub-millimiter absorbing
material in order to decrease the scattering inside it.
Focal plane layout[edit]
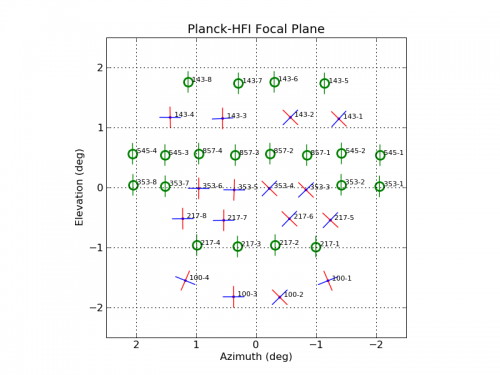
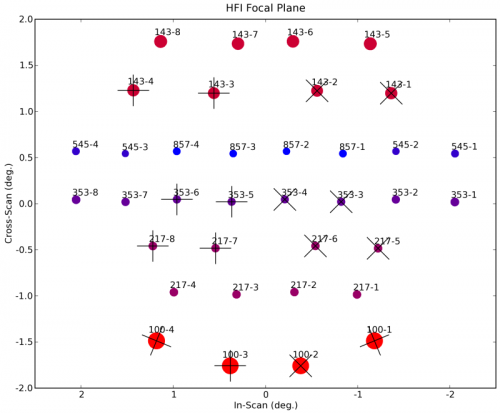
The layout of the detectors in the focal plane is defined to cope with the scanning strategy. The HFI horns are positioned at the centre of the focal plane, where the optical quality is good enough for the high frequencies. The curvature of rows compensates for the distortion of images by the telescope. A pair of identical SWB will scan the same circle on the sky to provide additional redundancy. Similar horns feeding PSBs are also aligned so that two pairs of PSBs rotated by 45◦ with respect to each other scan the same line. This will provide the Q and U Stokes parameters with minimal correction for the pointing (Rosset et al. 2010). Residual systematics will come from the differences between the beam shapes of the two horns. In all cases except for the 100 GHz horns, a measurement is also done by a pair of similar channels shifted by 1.25 arcminutes in the cross-scan direction, to ensure adequate sampling. In the figures focal plane layout is reported.
Readout[edit]
The AC bias readout electronics of the HFI instrument (Gaertner et al. 1997) includes a number of original features proposed by several laboratories (CRTBT in Grenoble, CESR in Toulouse and IAS in Orsay), which were validated on the Diabolo experiment and on the balloon-borne Archeops experiment. It was developed for space by the CESR in Toulouse.
The particular features of the HFI AC bias readout are mainly
- i)that the cold load resistors were replaced by capacitors because they have no Johnson noise;
- ii)that the detectors are biased by applying a triangular voltage to the load capacitors
which produces a square current [Ibias ] in the capacitors, and a square voltage [T bias ] that compensates for the stray capacitance of the wiring (producing a nearly square bias current into the bolometer;
- iii)that a square offset com-pensation signal is subtracted to the bolometric signal to minimise the amplitude of the signal that has to be amplified and digitized;
- iv)that the electronic scheme is symmetrical and uses a differential amplification scheme to optimize the immunity to electromagnetic interferences;
- v)and finally that every parameter of the REU can be set by commands, which
is made possible by using digital-to-analog and analog-to-digital converters extensively.
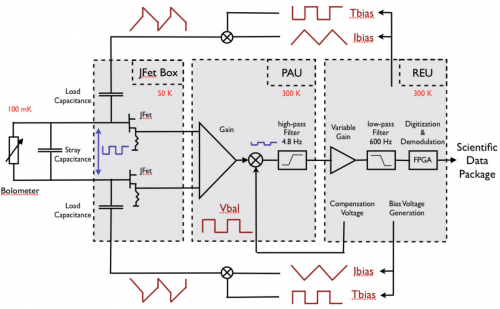
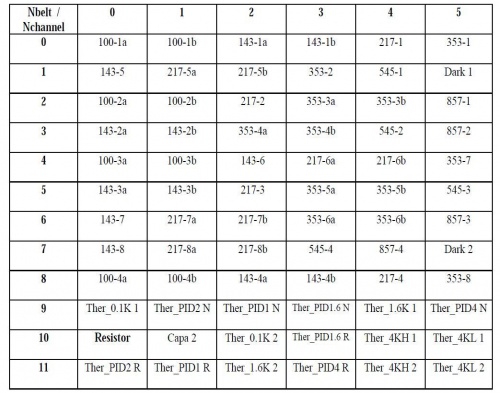
The readout electronics consist of 72 channels designed to perform low noise measurements of the impedance of 52 bolometers, two blind bolometers, 16 accurate low temperature thermometers, all in the 10 MΩ range, one resistor of 10 MΩ and one capacitor of 100 pF. The semiconductor bolometers and thermometers of Planck-HFI operate at cryogenic temperature around 100 mK on the focal plane, with impedance of about 10 MΩ when biased at the optimal current. The readout electronics on the contrary have to operate at “room” temperature (300 K). The distance between the two extremities of the readout chain is about 10 m and could represent a point of extreme susceptibility to electromagnetic interference. The readout electronic chain was split into three boxes. These are the JFET box, located on the 50 K stage of the satellite at 2.2 m from the focal plane, the pre-amplifier unit (PAU), located 1.8m further at 300 K, and the REU, located on the opposite side of the satellite, 5 m away. Each of the three boxes (JFET, PAU and
REU) consists of 12 belts of six channels. The first nine belts are dedicated to the bolometers, and the three last ones to the accurate thermometers, the resistor and the capacitor (see figure Organization of the HFI readout).
Principles of the readout electronics.[edit]
See figure [Principles of readout electronics]. The bolometer is biased by a square wave AC current obtained by the differentiation of a triangular voltage through a load capacitance, in a completely differential architecture. The presence of the stray capacitance due to losses of charge in the wiring requires a correction of the shape of the square bias current by a transient voltage. Thus the bias voltage generation is controlled by the two parameters I-bias and T-bias that express the amplitude of the triangular and transient voltage. The compensation voltage added to the bolometric signal to optimize the dynamic of the chain is controlled by the V-bal parameter.
Parameters of the Readout Unit can be set to optimize the detectors performance.
The modulation frequency of the AC bias system, fmod of the square bias current can be tuned from 70 Hz to 112 Hz by the telecommand parameters: Nsample, which defines the number of samples per half period of modulated signal, fdiv which determines the sampling frequency of the ADC.
The optimal frequencies are around 90 Hz.
Each channel has its own settings for the following parameters:
I-bias, amplitude of the triangular bias voltage;
T-bias, amplitude of the transient bias voltage;
V-bal, amplitude of the square compensation voltage;
G-amp, value of the programmable gain of the REU [1/3, 1, 3, 7.6];
N-blank, number of blanked samples at the beginning of halfperiod not taken into account during integration of the signal;
S-phase, phase shift when computing the integrated signal.
All these parameters influence the effective response of the detection chains, and were optimized during the calibration campaigns and confirmed during the calibration and performance verification (CPV) phase following the launch of Planck. The scientific signal is provided by the integral of the signal on each half-period, between limits fixed by the S-phase and N-blank parameters.
The interaction of modulated readout electronics with semiconductor
bolometers is rather different from that of a classical
DC bias readout (Jones 1953). The differences were seen during
the calibration of the HFI, although the readout electronics
was designed to mimic the operation
of a DC biased bolometric system as far as possible. With the
AC readout the maximum of responsivity is lower and is obtained
for higher bias current in the bolometer with respect to the DC model.
This is caused by the stray capacitance in the
wiring which has negligible effects for a DC bias and a major
effect for an AC bias. In our case, a stray capacitance of 150 pF
induces increases of NEP ranging from 4% (857 GHz bolometers)
to 10% (100 GHz bolometers) and also affects the HFI time
response. Details of the effect of the HFI AC bias system into
the time response of the detectors are discussed in the
Time Response Section.
JFETs[edit]
Given the high impedance of the bolometers and the length of the connecting cables, it it is essential that the impedance of the signal is lowered as close as possible to the detectors. In our system this is accomplished by means of JFET source followers, located in boxes connected to the 50 K stage. The JFET box has been designed, developed and tested in the Observational Cosmology group in the Physics Department of the University of Rome "La Sapienza" (Brienza D. et al 2006). There are two JFETs per channel, since the readout is fully differential, and they provide a current amplification of the signal while keeping the voltage amplification very close to unity.
Inside the box, the JFETs are mounted on a thermally insulated plate with an active temperature control to keep them at the optimal temperature of 110 K. With a dissipated power lower than 240 mW, mainly produced by the JFETs and the source resistors, we obtained a noise power spectral density of less than 3 nV Hz1/2 for the frequency range of interest. This increases the total noise ofall bolometer channels by less than 5%.
Data compression[edit]
The output of the readout electronics unit (REU) consists of one value for each of the 72 science channels for each half-period of modulation. This number, , is the sum of the 40 16-bit ADC signal values obtained within the given half-period. The data processor unit (DPU) performs a lossy quantization of .
We define a compression slice of 254 values, corresponding to about 1.4 s of observation for each detector and to a strip of sky about 8 degrees long. The mean of the data within each compression slice is computed, and data are demodulated using this mean:
where is the running index within the compression slice.
The mean of the demodulated data is computed and subtracted, and the resulting data slice is quantized according to a step size Q that is fixed per detector:
This is the lossy part of the algorithm: the required compression factor, obtained through the tuning of the quantization step Q, adds a measure of noise to the data. Assuming Gaussian white noise with standard deviation , a quantization setting of /Q = 2 adds 1% to the noise (Pajot et al. 2010; Pratt 1978). The value of was determined at the end of the CPV phase after subtraction of the signal from the timeline.
The two means and are computed as 32-bit words and sent through the telemetry, together with the values. Variable-length encoding of the values is performed on board, and the inverse decoding is applied on ground.
Optimal use of the bandpass available for the downlink (75 kb/s
average for HFI science) was obtained initially by using a value
of Q = /2.5 for all bolometer signals.
After 12 December 2009, only for the 857 GHz detectors, the
value was reset to Q = /2.0 to avoid data loss
due to exceeding the limit of downlink rate.
Time_response[edit]
The HFI bolometers and readout electronics have a finite response time to changes in incident optical power. The bolometers are thermal detectors of radiation whose response time is determined by the thermal circuit defined by the heat capacity of the detector and thermal conductivity.
Due to Planck's nearly constant scan rate, the time response is degenerate with the optical beam. However, because of the long time scale effects present in the time response, the time response is deconvolved from the data in the processing of the HFI data (see TOI processing).
The time response of the HFI bolometers and readout electronics is modeled as a Fourier domain transfer function (called the LFER4 model) consisting of the product of an bolometer thermal response and an electronics response .
LFER4 model[edit]
If we write the input signal (power) on a bolometer as the bolometer physical impedance can be written as: where is the angular frequency of the signal and is the complex intrinsic bolometer transfer function. For HFI the bolometer transfer function is modelled as the sum of 4 single pole low pass filters: The modulation of the signal is done with a square wave, written here as a composition of sine waves of decreasing amplitude: where we have used the Euler relation and is the angular frequency of the square wave. The modulation frequency is and was set to Hz in flight. This signal is then filtered by the complex electronic transfer function . Setting: we have: This signal is then sampled at high frequency (). is one of the parameters of the HFI electronics and corresponds to the number of high frequency samples in each modulation semi-period. In order to obtain an output signal sampled every seconds, we must integrate on a semiperiod, as done in the HFI readout. To also include a time shift , the integral is calculated between and (with period of the modulation). The time shift is encoded in the HFI electronics by the parameter , with the relation .
After integration, the -sample of a bolometer can be written as where
The output signal in equation eqn:output can be demodulated (thus removing the ) and compared to the input signal in equation bol_in. The overall transfer function is composed of the bolometer transfer function and the effective electronics transfer function, :
The shape of is obtained combining low and high-pass filters with Sallen Key topologies (with their respective time constants) and accounting also for the stray capacitance low pass filter given by the bolometer impedance combined with the stray capacitance of the cables. The sequence of filters that define the electronic band-pass function are listed in table table:readout_electronics_filters.
Parameters of LFER4 model[edit]
The LFER4 model has are a total of 10 parameters(,,,,,,,,,) 9 of which are independent, for each bolometer. The free parameters of the LFER4 model are determined using in-flight data in the following ways:
- is fixed at the value of the REU setting.
- is measured during the QEC test during CPV.
- , , , are fit forcing the compactness of the scanning beam.
- , , are fit by forcing agreement of survey 2 and survey 1 maps.
- The overall normalization of the LFER4 model is forced to be 1.0 at the signal frequency of the dipole.
The details of determining the model parameters are given in (reference P03c paper) and the best-fit parameters listed here in table table:LFER4pars.
HFI electronics filter sequence[edit]
| Filter | Parameters | Function |
|---|---|---|
| 0. Stray capacitance low pass filter | ||
| 1. Low pass filter | k nF |
|
| 2. Sallen Key high pass filter | k |
3 |
| 3. Sign reverse with gain | ||
| 4. Single pole low pass filter with gain | k nF |
|
| 5. Single pole high pass filter coupled to a Sallen Key low pass filter | k k nF k F |
| Bolometer | (s) | (s) | (s) | (s) | (s) | (s) | ||||
| 100-1a | 0.392 | 0.01 | 0.534 | 0.0209 | 0.0656 | 0.0513 | 0.00833 | 0.572 | 0.00159 | 0.00139 |
| 100-1b | 0.484 | 0.0103 | 0.463 | 0.0192 | 0.0451 | 0.0714 | 0.00808 | 0.594 | 0.00149 | 0.00139 |
| 100-2a | 0.474 | 0.00684 | 0.421 | 0.0136 | 0.0942 | 0.0376 | 0.0106 | 0.346 | 0.00132 | 0.00125 |
| 100-2b | 0.126 | 0.00584 | 0.717 | 0.0151 | 0.142 | 0.0351 | 0.0145 | 0.293 | 0.00138 | 0.00125 |
| 100-3a | 0.744 | 0.00539 | 0.223 | 0.0147 | 0.0262 | 0.0586 | 0.00636 | 0.907 | 0.00142 | 0.00125 |
| 100-3b | 0.608 | 0.00548 | 0.352 | 0.0155 | 0.0321 | 0.0636 | 0.00821 | 0.504 | 0.00166 | 0.00125 |
| 100-4a | 0.411 | 0.0082 | 0.514 | 0.0178 | 0.0581 | 0.0579 | 0.0168 | 0.37 | 0.00125 | 0.00125 |
| 100-4b | 0.687 | 0.0113 | 0.282 | 0.0243 | 0.0218 | 0.062 | 0.00875 | 0.431 | 0.00138 | 0.00139 |
| 143-1a | 0.817 | 0.00447 | 0.144 | 0.0121 | 0.0293 | 0.0387 | 0.0101 | 0.472 | 0.00142 | 0.00125 |
| 143-1b | 0.49 | 0.00472 | 0.333 | 0.0156 | 0.134 | 0.0481 | 0.0435 | 0.27 | 0.00149 | 0.00125 |
| 143-2a | 0.909 | 0.0047 | 0.0763 | 0.017 | 0.00634 | 0.1 | 0.00871 | 0.363 | 0.00148 | 0.00125 |
| 143-2b | 0.912 | 0.00524 | 0.0509 | 0.0167 | 0.0244 | 0.0265 | 0.0123 | 0.295 | 0.00146 | 0.00125 |
| 143-3a | 0.681 | 0.00419 | 0.273 | 0.00956 | 0.0345 | 0.0348 | 0.0115 | 0.317 | 0.00145 | 0.00125 |
| 143-3b | 0.82 | 0.00448 | 0.131 | 0.0132 | 0.0354 | 0.0351 | 0.0133 | 0.283 | 0.00161 | 0.000832 |
| 143-4a | 0.914 | 0.00569 | 0.072 | 0.0189 | 0.00602 | 0.0482 | 0.00756 | 0.225 | 0.00159 | 0.00125 |
| 143-4b | 0.428 | 0.00606 | 0.508 | 0.00606 | 0.0554 | 0.0227 | 0.00882 | 0.084 | 0.00182 | 0.00125 |
| 143-5 | 0.491 | 0.00664 | 0.397 | 0.00664 | 0.0962 | 0.0264 | 0.0156 | 0.336 | 0.00202 | 0.00139 |
| 143-6 | 0.518 | 0.00551 | 0.409 | 0.00551 | 0.0614 | 0.0266 | 0.0116 | 0.314 | 0.00153 | 0.00111 |
| 143-7 | 0.414 | 0.00543 | 0.562 | 0.00543 | 0.0185 | 0.0449 | 0.00545 | 0.314 | 0.00186 | 0.00139 |
| 217-5a | 0.905 | 0.00669 | 0.0797 | 0.0216 | 0.00585 | 0.0658 | 0.00986 | 0.342 | 0.00157 | 0.00111 |
| 217-5b | 0.925 | 0.00576 | 0.061 | 0.018 | 0.00513 | 0.0656 | 0.0094 | 0.287 | 0.00187 | 0.00125 |
| 217-6a | 0.844 | 0.00645 | 0.0675 | 0.0197 | 0.0737 | 0.0316 | 0.0147 | 0.297 | 0.00154 | 0.00125 |
| 217-6b | 0.284 | 0.00623 | 0.666 | 0.00623 | 0.0384 | 0.024 | 0.0117 | 0.15 | 0.00146 | 0.00111 |
| 217-7a | 0.343 | 0.00548 | 0.574 | 0.00548 | 0.0717 | 0.023 | 0.0107 | 0.32 | 0.00152 | 0.00139 |
| 217-7b | 0.846 | 0.00507 | 0.127 | 0.0144 | 0.0131 | 0.0479 | 0.0133 | 0.311 | 0.00151 | 0.00139 |
| 217-8a | 0.496 | 0.00722 | 0.439 | 0.00722 | 0.0521 | 0.0325 | 0.0128 | 0.382 | 0.00179 | 0.00111 |
| 217-8b | 0.512 | 0.00703 | 0.41 | 0.00703 | 0.0639 | 0.0272 | 0.0139 | 0.232 | 0.00173 | 0.00125 |
| 217-1 | 0.0136 | 0.00346 | 0.956 | 0.00346 | 0.0271 | 0.0233 | 0.00359 | 1.98 | 0.00159 | 0.00111 |
| 217-2 | 0.978 | 0.00352 | 0.014 | 0.0261 | 0.00614 | 0.042 | 0.00194 | 0.686 | 0.0016 | 0.00125 |
| 217-3 | 0.932 | 0.00355 | 0.0336 | 0.00355 | 0.0292 | 0.0324 | 0.00491 | 0.279 | 0.00174 | 0.00125 |
| 217-4 | 0.658 | 0.00135 | 0.32 | 0.00555 | 0.0174 | 0.0268 | 0.00424 | 0.473 | 0.00171 | 0.00111 |
| 353-3a | 0.554 | 0.00704 | 0.36 | 0.00704 | 0.0699 | 0.0305 | 0.0163 | 0.344 | 0.0017 | 0.00125 |
| 353-3b | 0.219 | 0.00268 | 0.671 | 0.00695 | 0.0977 | 0.0238 | 0.0119 | 0.289 | 0.00157 | 0.00111 |
| 353-4a | 0.768 | 0.00473 | 0.198 | 0.00993 | 0.0283 | 0.0505 | 0.00628 | 0.536 | 0.00181 | 0.00125 |
| 353-4b | 0.684 | 0.00454 | 0.224 | 0.0108 | 0.0774 | 0.08 | 0.0149 | 0.267 | 0.00166 | 0.00111 |
| 353-5a | 0.767 | 0.00596 | 0.159 | 0.0124 | 0.0628 | 0.0303 | 0.0109 | 0.357 | 0.00156 | 0.00111 |
| 353-5b | 0.832 | 0.00619 | 0.126 | 0.0111 | 0.0324 | 0.035 | 0.0096 | 0.397 | 0.00166 | 0.00111 |
| 353-6a | 0.0487 | 0.00176 | 0.855 | 0.006 | 0.0856 | 0.0216 | 0.0105 | 0.222 | 0.00199 | 0.00125 |
| 353-6b | 0.829 | 0.00561 | 0.127 | 0.00561 | 0.0373 | 0.0252 | 0.00696 | 0.36 | 0.00228 | 0.00111 |
| 353-1 | 0.41 | 0.000743 | 0.502 | 0.00422 | 0.0811 | 0.0177 | 0.0063 | 0.329 | 0.00132 | 0.00097 |
| 353-2 | 0.747 | 0.00309 | 0.225 | 0.00726 | 0.0252 | 0.0447 | 0.00267 | 0.513 | 0.00154 | 0.00097 |
| 353-7 | 0.448 | 0.0009 | 0.537 | 0.0041 | 0.0122 | 0.0273 | 0.00346 | 0.433 | 0.00178 | 0.00125 |
| 353-8 | 0.718 | 0.00223 | 0.261 | 0.00608 | 0.0165 | 0.038 | 0.00408 | 0.268 | 0.00177 | 0.00111 |
| 545-1 | 0.991 | 0.00293 | 0.00743 | 0.026 | 0.00139 | 2.6 | 0 | 0 | 0.00216 | 0.00111 |
| 545-2 | 0.985 | 0.00277 | 0.0128 | 0.024 | 0.00246 | 2.8 | 0 | 0 | 0.00187 | 0.00097 |
| 545-4 | 0.972 | 0.003 | 0.0277 | 0.025 | 0.000777 | 2.5 | 0 | 0 | 0.00222 | 0.00111 |
| 857-1 | 0.974 | 0.00338 | 0.0229 | 0.025 | 0.00349 | 2.2 | 0 | 0 | 0.00176 | 0.00111 |
| 857-2 | 0.84 | 0.00148 | 0.158 | 0.00656 | 0.00249 | 3.2 | 0 | 0 | 0.0022 | 0.00125 |
| 857-3 | 0.36 | 4.22e-05 | 0.627 | 0.0024 | 0.0111 | 0.017 | 0.002 | 1.9 | 0.00152 | 0.00126 |
| 857-4 | 0.278 | 0.0004 | 0.719 | 0.00392 | 0.00162 | 0.09 | 0.00152 | 0.8 | 0.00149 | 0.000558 |
Operations[edit]
(Vibert)
This page lists the events which have or might have affected the data stability.
System (Ken)[edit]
List of systematics[edit]
Like all experiments, Planck/HFI had a number of "issues" which it needed to track and verify were not compromising the data. While these are discussed in appropriate sections, here we gather them together to give brief summaries of the issues and refer the reader to the appropriate section for more details.
- Cosmic Rays - Unprotected by the atmosphere and more sensitive than previous bolometric experiment, HFI was subjected to many more cosmic ray hits than previous experiments. These were detected, the worst parts of the data flagged as unusable, and "tails" were modeled and removed. This is described in XXXXX
- Elephants - Cosmic rays also hit the 100 mK stage and cause the temperature to vary, inducing small temperature and thus noise variations in the detectors. This is described in XXXXX
- 1.6 K Stage Fluctuations
- 4 K Stage Fluctuations
- Popcorn Noise - Some channels were occasionally affected by what seems to be a "split-level" noise, which has been variously called popcorn noise or random telegraphic signal. These data are usually flagged. This is described in XXXXX
- Jumps - Similar to but distinct from popcorn noise, small jumps were occasionally found in the data streams. These data are usually corrected. This is described in XXXXX.
- 4 K Cooler-Induced EM Noise - The 4 K cooler induced noise in the detectors with very specific frequency signatures, which is filtered. This is described in XXXXX.
- 4 K Cooler-Induced Microphonics - The mechanical cooler was shown in XXXXX to cause very little microphonic parasites in the detector data.
- Pointing-Change Microphonics - The changes in pointing after each pointing period were shown in XXXXX to cause very little microphonic parasitic signal in the detector data.
- Compression - Onboard compression is used to overcome our telemetry bandwidth limitations. This is explained in XXXXX.
- Noise Correlations - Correlations in noise between detectors seems to be negligble but for two polarization sensitive detectors in the same horn. This is discussed in XXXXX.
- Electrical Cross-Talk - Cross-talk is discussed in XXXXX.
- Pointing - The final pointing reconstruction for Planck is near the arcsecond level. This is discussed in XXXXX.
- Focal Plane Geometry - The relative positions of different horns in the focal plane is reconstructed using planets. This is discussed in XXXXX.
- Main Beam - The main beams for HFI are discussed in XXXXX.
- Ruze Envelope - Random imperfections or dust on the mirrors can increase the size of the beam a bit. This is discussed in XXXXX.
- Dimpling - The mirror support structure causes a pattern of small imperfections in the beams, which cause small sidelobe responses outside the main beam. This is discussed in XXXXX.
- Far Sidelobes - Small amounts of light can sometimes hit the detectors from just above the primary or secondary mirrors, or even from reflecting off the baffles. While small, when the Galactic center is in the right position, this can be detected in the highest frequency channels, so this is removed from the data. This is discussed in XXXXX.
- Planet Fluxes - Comparing the known fluxes of planets with the calibration on the CMB dipole is a useful check of calibration. This is done in XXXXX.
- Point Source Fluxes - As with planet fluxes, we also compare fluxes of known, bright point sources with the CMB dipole calibration. This is done in XXXXX.
- Time Constants - The HFI bolometers do not react instantaneously to light; there are small time constants, discussed XXXXX.
- ADC Correction - The HFI Analog-to-Digital Converters are not perfect, and are not used perfectly. Their effects on the calibration are discussed in XXXXX.
- Gain changes with Temperature Changes
- Optical Cross-Talk - This is discussed in XXXXX.
- Bandpass - The transmission curves, or "bandpass" has shown up in a number of places. This is discussed in XXXXX and YYYYY.
- Saturation - While this is mostly an issue only for Jupiter observations, it should be remembered that the HFI detectors cannot observe arbitrarily bright objects. This is discussed in XXXXX.
Summary[edit]
(Lamarre) here remind worse sytematics and point to DPC Summary of sucess and limitations. JML. Link to early HFI in flight perf.
Annexes[edit]
(Vibert)
This page lists all annexes related to the HFI design, qualification and performance.
(Planck) High Frequency Instrument
Junction Field Elect Transistor
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
(Planck) Low Frequency Instrument
Calibration and Performance Verification
Back To Back HFI horns
Cosmic Microwave background
LFI Waveguide
Instrument Line Shape
Full-Width-at-Half-Maximum
Planck Legacy Archive
Readout Electronic Unit
Pre_Amplification Unit
analog to digital converter
Noise Equivalent Power
Data Processing Unit
Data Processing Center