Difference between revisions of "Beams LFI"
m |
(→Main Beams and Focal Plane calibration) |
||
| Line 47: | Line 47: | ||
* Electromagnetic simulation (using GRASP Physical Optics code) by appropriately tuning the Radio Frequency Flight Model (RFFM) <cite>#tauber2010b</cite>. The Radio Frequency Tuned Model, called RFTM, was implemented to fit the beam data with electromagnetic model. It is derived as follow: | * Electromagnetic simulation (using GRASP Physical Optics code) by appropriately tuning the Radio Frequency Flight Model (RFFM) <cite>#tauber2010b</cite>. The Radio Frequency Tuned Model, called RFTM, was implemented to fit the beam data with electromagnetic model. It is derived as follow: | ||
| − | ** | + | **the Focal plane unit electromagnetic model has shifted by 3.5mm toward the secondary mirror; |
| − | **each feed horn phase centre has been moved alogn horn axis to optimize the match between simulations and data | + | **for the 30GHz channel, the center frequency of the simulated monochromatic beams have been chosen according to the centre frequency of the RIMO; for the 44 and 70 GHz channels the center frequency is the nominal one. |
| − | ** center frequency of the | + | **each feed horn phase centre has been moved alogn horn axis to optimize the match between simulations and data. The optimization was obtained by minimizing the variance according to the following definition: If $B_s[u,v]$ is the peak-normalized scanning beam matrix (for semplicity we use here $(u,v)$ coordinates also as indexes of the beam matrix) and $B_o[u,v]$ is the smeared peak-normalized simulated GRASP beam, the variance, $\sigma$, can be evaluated for each beam: |
| + | \begin{eqnarray} | ||
| + | \label{eqsigma} | ||
| + | \sigma &=& {\sum_{u,v}{(f[u,v] - \overline{f})^2}}\cdot {1\over N} \\ | ||
| + | f[u,v]&=&w[u,v] \cdot (B^{dB}_s(u,v)- B^{dB}_o(u,v)) \\ | ||
| + | w[u,v]&=&\sqrt{T_a[u,v]} | ||
| + | \end{eqnarray} | ||
| + | |||
| + | % v=1./count*total((f-mean(f))^2) | ||
| + | % f=w*(10*alog10(mb/max(mb))-10*alog10(sb/max(sb))) | ||
| + | where also $T_a[u,v]$ is the antenna temperature or the scanning beam not normalized to peak, and $N$ is the number of points considered in the comparison so that the number of point in the (u,v) plane. The parameter $\sigma$ is the variance of the difference between two beams weighted by the measured beam itself. For each beam the variance has computed computed down to $-15$dB from beam peak to avoid bias due to noise. The calculations were applied to four telescope models listed hereafter: | ||
| + | |||
| + | \begin{itemize} | ||
| + | \item[(a)] Radio Frequency Flight Model (RFFM). The model is described in \citep{tauber2010b} and it is based on the pre-launch knowledge, i.e. shape of reflectors, alignment, and horns as estimated form hardware development, alignment campaign, and thermo-elastic model of the payload. | ||
| + | \item[(b)] Design Model (RFDM). The model that is based on design mirrors (perfect surfaces and aligment) and design Focal Plane Unit (nominal position and orientation of the feedhorns). | ||
| + | \item[(c)] Radio Frequency Hybrid Model (RFHM). This model is based on the RFFM mirror's arrangement coupled with the design Focal Plane Unit. | ||
| + | \item[(d)] Radio Frequency Shimmed Model (RFSM). This model is based is based on the RFFM model but with the Focal Plane Unit shimmed at $3.5$ mm towards the secondary reflector. | ||
| + | \end{itemize} | ||
| + | |||
| + | From Fig.\ref{fig:compmodels} which shows the comparison between the \texttt{LFI18M} measured beam and the four telescope models, it is evident that the RFDM fit better the measurements than the RFFM and that the best agreement has found with the RFSM. In Sandri et al. 2012 %(\cite{Sandri 2012}) % citare la Nota tecnica di sandri sull'rffm ecc. | ||
| + | it has been demonstrated that this behavior is the same far all the 22 beams allowing us to assume the RFSM as the reference model for further optimizations. | ||
| + | Then an additional tuning was performed minimizing the variance by varying the phase center of each feed in the RFSM, obtaining the model listed here: | ||
| + | |||
| + | \begin{itemize} | ||
| + | \item[(e)] Radio Frequency Tuned Model (RFTM). This model is based on the RFSM but with each Horn phase center definition optimized to minimize the variance in Eq. \ref{eqsigma}. | ||
| + | \end{itemize} | ||
| + | |||
| + | All the comparison and beams where monochromatic, i.e calculated at a single frequency called Optical Center Frequency (OCF). For the model (a), (b), (c) and (d) the OCF is the nominal center frequency ($30.0$, $44.0$ and $70.0$ GHz). For the model (a) is $28.0$, $44.0$, $70.0$. In fact the optical and radiometer bandshapes as reported in \cite{zonca2009} demonstrates that for the 30 GHz channel, the radiometer responses are better described by a central frequency closer to 28 GHz with respect to the nominal one, whereas for the other two frequency channels the OCF is close to the nominal one. Fig.~\ref{fig:comp} shows the measurement superimposed to the smeared optical beams of the RFTM for some of the LFI beams. In Fig.~\ref{fig:comp70} the maps obtained from the difference between measurements and simulations for the 70 GHz beams (main arm) are also shown; the same comparison has been plotted for the \texttt{LFI26} at 44 GHz in Fig. \ref{fig:comp26} shows | ||
| + | |||
| + | \begin{figure}[!h] | ||
| + | \centering | ||
| + | \begin{tabular}{cc} | ||
| + | \includegraphics[width=4cm]{images/c0.jpg} & | ||
| + | \includegraphics[width=4cm]{images/c1.jpg} \\ | ||
| + | \includegraphics[width=4cm]{images/c2.jpg} & | ||
| + | \includegraphics[width=4cm]{images/c3.jpg} \\ | ||
| + | \end{tabular} | ||
| + | \caption{\texttt{LFI18M} beam derived from the four models described in Section \ref{optical_beams} compared with the measured scanning beam (white contours). the RFFM (a) is in blue, the RFDM (b) is in red, the | ||
| + | RFHB (c) is in cyan, and the RFSM (d) is in green. Contours are $-3$, $-10$, $-15$, $-20$ dB. } | ||
| + | \label{fig:compmodels} | ||
| + | \end{figure} | ||
| + | |||
| + | \begin{figure}[!h] | ||
| + | \centering | ||
| + | \includegraphics[width=8.4cm]{images/comp_rffm_tsv.png} | ||
| + | \caption{Comparison between the beams derived from the RFTM (coloured contours) and the flight measurements (black contours). Contours are at $-20$, $-15$, $-10$, $-6$, $-3$ at 70 GHz; $-15$, $-10$, $-6$, $-3$ at 44 and 30 GHz). } | ||
| + | \label{fig:comp} | ||
| + | \end{figure} | ||
| + | |||
| + | \subsection{Beam validation through deconvolution} | ||
| + | |||
| + | To test the goodness of the beam representation, the maps for each individual horn at 30 GHz and 44 GHz were | ||
| + | deconvolved using the ArtDeco beam deconvolution algorithm described in \citet{keihanen2012}. %Keih\"anen \& Reinecke (2012). | ||
| + | The code takes as input the time-ordered data stream, along with pointing information and the harmonic representation | ||
| + | of the beam, and constructs the harmonic $a_{slm}$ coefficients that represent the sky signal. | ||
| + | We use the scanning beams, which have been smeared to take into account the motion of the satellite. | ||
| + | From the harmonic coefficients we further construct a sky map, which is now be free from effects of beam asymmetry, | ||
| + | given that our beam representation is correct. | ||
| + | |||
| + | Before deconvolution we run the time-ordered data through the Madam map-making code (Keih\"anen et al, 2010), | ||
| + | to remove low-frequency noise. | ||
| + | We saved the baselines that represent the correlated noise component, | ||
| + | and subtracted them from the original data stream. The cleaned data consists of signal and a residual noise component, | ||
| + | which is dominated by white noise. This was provided as input to the deconvolution code. | ||
| + | |||
| + | We run deconvolution on data from each single survey, and looked at residual differences between single-survey maps. | ||
| + | Results for horn LFI26 (44 GHz) are shown in Fig. \ref{fig:deconvolution}. | ||
| + | Shown is the difference between first and second survey maps. | ||
| + | The left-hand column shows a zoom into the galactic region in location (0,0). One image covers a square of width 13.3 deg. | ||
| + | The right-hand column shows a zoom into a point source near location (-90,0). The width of this image is 16.7 deg. | ||
| + | In absence of beam asymmetry and other systematics the difference should contain noise only. | ||
| + | |||
| + | The top row shows for comparison the difference between binned maps. In this case the maps were binned directly | ||
| + | from the time-ordered data, without attempt to correct for beam effects. | ||
| + | A given region on the sky is scanned in different orientations of the beam during different surveys. | ||
| + | This gives rise to the residual galactic signal that is evident in the top row images. | ||
| + | |||
| + | The maps were smoothed to 1 degree (FWHM) resolution, in order to suppress noise. | ||
| + | In the case of binned maps this was achieved by applying smoothing by | ||
| + | a symmetric Gaussian beam with FWHM of 50 arcmin. Combined with the width of the radiometer beam, | ||
| + | this gives a total smoothing of approximately one degree. | ||
| + | |||
| + | The bottom row shows the corresponding difference of deconvolved maps. | ||
| + | We show the same regions as in the top row, with same scaling. | ||
| + | We smoothed the deconvolved harmonic coefficients with 1 deg (FWHM) Gaussian beam, and constructed a sky map through harmonic expansion. | ||
| + | Deconvolution removes the galactic residual, as well as the ``butterfly'' pattern of the point source almost completely. | ||
| + | This indicates that the simulated monochromatic beams based on RFTM - model (e) - represent well the true beam. | ||
== Effective beams == | == Effective beams == | ||
Revision as of 15:20, 12 March 2013
Contents
Overview[edit]
LFI is observing the sky with 11 pairs of beams associated with the 22 pseudo-correlation radiometers. Each beam of the radiometer pair (Radiometer Chain Assembly - RCA) is named as LFIXXM or LFIXXS. XX is the RCA number ranging from 18 to 28; M and S are the two polarization namely main-arm and side-arm of the Orthomode transducers #darcangelo2009b (see also LFI naming convention).
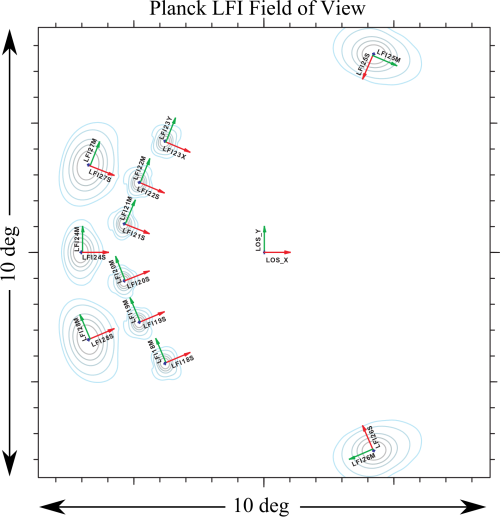
Main Beams and Focal Plane calibration[edit]
As the focal plane calibration we refer to the determination of the beam pointing parameters in the nominal Line of Sight (LOS) frame through main beam measurments using Jupiter transits. the parametes that characterise the beam pointing are the following:
- THETA_UV ($\theta_{uv}$)
- PHI_UV ($\phi_{uv}$)
They are calculated starting from u,v coordinates derived form the beam reconstruction algorithm as
$\theta_{uv} = \arcsin(u^2+v^2)$
$\phi_{uv} = \arctan(v/u)$
Two additional angles are used to characterize the beams in the RIMO:
- PSI_UV ($\psi_{uv}$)
- PSI_POL ($\psi_{pol}$)
$\psi_{uv}$ and $\psi_{pol}$ are not derived from measurements but they are extimated form optical simulations. They are the quantities that represent the polarization direction of each beam, in the following approximation: the M- and S- beams of the same RCA point at the same direction on the sky.
The main beams are characterised by 2 method:
- elliptical (or bivariate) gaussian fit as in #[planck2011-1-6] with modification explained in #[planck2013-p02d]. This method is used to determine
- the beam centre
- the average full width half maximum defined as $\sqrt{FWHM_{max}\cdot FWHM_{min}}$
- the beam ellipticity defined as $FWHM_{max}\over{FWHM_{min}}$
- the beam tilting, $\psi_{ell}$, with respect the u-axis.
- Electromagnetic simulation (using GRASP Physical Optics code) by appropriately tuning the Radio Frequency Flight Model (RFFM) #tauber2010b. The Radio Frequency Tuned Model, called RFTM, was implemented to fit the beam data with electromagnetic model. It is derived as follow:
- the Focal plane unit electromagnetic model has shifted by 3.5mm toward the secondary mirror;
- for the 30GHz channel, the center frequency of the simulated monochromatic beams have been chosen according to the centre frequency of the RIMO; for the 44 and 70 GHz channels the center frequency is the nominal one.
- each feed horn phase centre has been moved alogn horn axis to optimize the match between simulations and data. The optimization was obtained by minimizing the variance according to the following definition: If $B_s[u,v]$ is the peak-normalized scanning beam matrix (for semplicity we use here $(u,v)$ coordinates also as indexes of the beam matrix) and $B_o[u,v]$ is the smeared peak-normalized simulated GRASP beam, the variance, $\sigma$, can be evaluated for each beam:
\begin{eqnarray} \label{eqsigma} \sigma &=& {\sum_{u,v}{(f[u,v] - \overline{f})^2}}\cdot {1\over N} \\ f[u,v]&=&w[u,v] \cdot (B^{dB}_s(u,v)- B^{dB}_o(u,v)) \\ w[u,v]&=&\sqrt{T_a[u,v]} \end{eqnarray}
% v=1./count*total((f-mean(f))^2) % f=w*(10*alog10(mb/max(mb))-10*alog10(sb/max(sb))) where also $T_a[u,v]$ is the antenna temperature or the scanning beam not normalized to peak, and $N$ is the number of points considered in the comparison so that the number of point in the (u,v) plane. The parameter $\sigma$ is the variance of the difference between two beams weighted by the measured beam itself. For each beam the variance has computed computed down to $-15$dB from beam peak to avoid bias due to noise. The calculations were applied to four telescope models listed hereafter:
\begin{itemize} \item[(a)] Radio Frequency Flight Model (RFFM). The model is described in \citep{tauber2010b} and it is based on the pre-launch knowledge, i.e. shape of reflectors, alignment, and horns as estimated form hardware development, alignment campaign, and thermo-elastic model of the payload. \item[(b)] Design Model (RFDM). The model that is based on design mirrors (perfect surfaces and aligment) and design Focal Plane Unit (nominal position and orientation of the feedhorns). \item[(c)] Radio Frequency Hybrid Model (RFHM). This model is based on the RFFM mirror's arrangement coupled with the design Focal Plane Unit. \item[(d)] Radio Frequency Shimmed Model (RFSM). This model is based is based on the RFFM model but with the Focal Plane Unit shimmed at $3.5$ mm towards the secondary reflector. \end{itemize}
From Fig.\ref{fig:compmodels} which shows the comparison between the \texttt{LFI18M} measured beam and the four telescope models, it is evident that the RFDM fit better the measurements than the RFFM and that the best agreement has found with the RFSM. In Sandri et al. 2012 %(\cite{Sandri 2012}) % citare la Nota tecnica di sandri sull'rffm ecc. it has been demonstrated that this behavior is the same far all the 22 beams allowing us to assume the RFSM as the reference model for further optimizations. Then an additional tuning was performed minimizing the variance by varying the phase center of each feed in the RFSM, obtaining the model listed here:
\begin{itemize} \item[(e)] Radio Frequency Tuned Model (RFTM). This model is based on the RFSM but with each Horn phase center definition optimized to minimize the variance in Eq. \ref{eqsigma}. \end{itemize}
All the comparison and beams where monochromatic, i.e calculated at a single frequency called Optical Center Frequency (OCF). For the model (a), (b), (c) and (d) the OCF is the nominal center frequency ($30.0$, $44.0$ and $70.0$ GHz). For the model (a) is $28.0$, $44.0$, $70.0$. In fact the optical and radiometer bandshapes as reported in \cite{zonca2009} demonstrates that for the 30 GHz channel, the radiometer responses are better described by a central frequency closer to 28 GHz with respect to the nominal one, whereas for the other two frequency channels the OCF is close to the nominal one. Fig.~\ref{fig:comp} shows the measurement superimposed to the smeared optical beams of the RFTM for some of the LFI beams. In Fig.~\ref{fig:comp70} the maps obtained from the difference between measurements and simulations for the 70 GHz beams (main arm) are also shown; the same comparison has been plotted for the \texttt{LFI26} at 44 GHz in Fig. \ref{fig:comp26} shows
\begin{figure}[!h] \centering \begin{tabular}{cc} \includegraphics[width=4cm]{images/c0.jpg} & \includegraphics[width=4cm]{images/c1.jpg} \\ \includegraphics[width=4cm]{images/c2.jpg} & \includegraphics[width=4cm]{images/c3.jpg} \\ \end{tabular} \caption{\texttt{LFI18M} beam derived from the four models described in Section \ref{optical_beams} compared with the measured scanning beam (white contours). the RFFM (a) is in blue, the RFDM (b) is in red, the RFHB (c) is in cyan, and the RFSM (d) is in green. Contours are $-3$, $-10$, $-15$, $-20$ dB. } \label{fig:compmodels} \end{figure}
\begin{figure}[!h] \centering \includegraphics[width=8.4cm]{images/comp_rffm_tsv.png} \caption{Comparison between the beams derived from the RFTM (coloured contours) and the flight measurements (black contours). Contours are at $-20$, $-15$, $-10$, $-6$, $-3$ at 70 GHz; $-15$, $-10$, $-6$, $-3$ at 44 and 30 GHz). } \label{fig:comp} \end{figure}
\subsection{Beam validation through deconvolution}
To test the goodness of the beam representation, the maps for each individual horn at 30 GHz and 44 GHz were deconvolved using the ArtDeco beam deconvolution algorithm described in \citet{keihanen2012}. %Keih\"anen \& Reinecke (2012). The code takes as input the time-ordered data stream, along with pointing information and the harmonic representation of the beam, and constructs the harmonic $a_{slm}$ coefficients that represent the sky signal. We use the scanning beams, which have been smeared to take into account the motion of the satellite. From the harmonic coefficients we further construct a sky map, which is now be free from effects of beam asymmetry, given that our beam representation is correct.
Before deconvolution we run the time-ordered data through the Madam map-making code (Keih\"anen et al, 2010), to remove low-frequency noise. We saved the baselines that represent the correlated noise component, and subtracted them from the original data stream. The cleaned data consists of signal and a residual noise component, which is dominated by white noise. This was provided as input to the deconvolution code.
We run deconvolution on data from each single survey, and looked at residual differences between single-survey maps. Results for horn LFI26 (44 GHz) are shown in Fig. \ref{fig:deconvolution}. Shown is the difference between first and second survey maps. The left-hand column shows a zoom into the galactic region in location (0,0). One image covers a square of width 13.3 deg. The right-hand column shows a zoom into a point source near location (-90,0). The width of this image is 16.7 deg. In absence of beam asymmetry and other systematics the difference should contain noise only.
The top row shows for comparison the difference between binned maps. In this case the maps were binned directly from the time-ordered data, without attempt to correct for beam effects. A given region on the sky is scanned in different orientations of the beam during different surveys. This gives rise to the residual galactic signal that is evident in the top row images.
The maps were smoothed to 1 degree (FWHM) resolution, in order to suppress noise. In the case of binned maps this was achieved by applying smoothing by a symmetric Gaussian beam with FWHM of 50 arcmin. Combined with the width of the radiometer beam, this gives a total smoothing of approximately one degree.
The bottom row shows the corresponding difference of deconvolved maps. We show the same regions as in the top row, with same scaling. We smoothed the deconvolved harmonic coefficients with 1 deg (FWHM) Gaussian beam, and constructed a sky map through harmonic expansion. Deconvolution removes the galactic residual, as well as the ``butterfly pattern of the point source almost completely. This indicates that the simulated monochromatic beams based on RFTM - model (e) - represent well the true beam.
Effective beams[edit]
TBW
Window Functions[edit]
TBW
Sidelobes[edit]
There is no direct measurements of sidelobes for LFI. The sidelobe pattern is estimated by simulations taking into account the geometry of the telescope and the satellite structure. In figure
References[edit]
<biblio force=false>
</biblio>
(Planck) Low Frequency Instrument
LFI Radiometer Chain Assembly
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
Line Of Sight
reduced IMO
Full-Width-at-Half-Maximum