Difference between revisions of "LFI systematic effect uncertainties"
(→ADC non linearity) |
|||
| (29 intermediate revisions by 4 users not shown) | |||
| Line 4: | Line 4: | ||
Known systematic effects in the Planck-LFI data can be divided into two broad categories: effects independent of the sky signal, which can be considered as additive or multiplicative spurious contributions to the measured timelines, and effects which are dependent on the sky and that cannot be considered independently from the observation strategy. | Known systematic effects in the Planck-LFI data can be divided into two broad categories: effects independent of the sky signal, which can be considered as additive or multiplicative spurious contributions to the measured timelines, and effects which are dependent on the sky and that cannot be considered independently from the observation strategy. | ||
| − | Here we report a brief summary of these effects, all the details can be found in {{PlanckPapers|planck2013-p02a}}. | + | Here we report a brief summary of these effects, all the details can be found in {{PlanckPapers|planck2013-p02a}} and {{PlanckPapers|planck2014-a04||Planck-2015-A04}}. |
==Summary of uncertainties due to systematic effects== | ==Summary of uncertainties due to systematic effects== | ||
In this section we provide a top-level overview of the uncertainties due to systematic effects in the Planck-LFI CMB temperature maps and power spectra. Table 1 provides a list of these effects with short indications of their cause, strategies for removal and references to sections and/or papers where more information is found. | In this section we provide a top-level overview of the uncertainties due to systematic effects in the Planck-LFI CMB temperature maps and power spectra. Table 1 provides a list of these effects with short indications of their cause, strategies for removal and references to sections and/or papers where more information is found. | ||
| + | |||
| + | {| border="1" cellspacing="0" cellpadding="2" align="center" | ||
| + | |+ <small>'''Table 1. List of known instrumental systematic effects in Planck LFI.'''</small> | ||
| + | |- | ||
| + | !scope="col"| Effect | ||
| + | !scope="col"| Source | ||
| + | !scope="col"| Control/Removal | ||
| + | !scope="col"| Reference | ||
| + | |- | ||
| + | !width="280" | Effects independent of sky signal (T and P) | ||
| + | |width="220" | | ||
| + | |width="220" | | ||
| + | |width="140" | | ||
| + | |- | ||
| + | |width="280" | White noise correlation | ||
| + | |width="220" | Phase-switch imbalance | ||
| + | |width="220" | Diode weighting | ||
| + | |width="140" | {{PlanckPapers|planck2013-p02a}} {{PlanckPapers|planck2014-a04||Planck-2015-A04}} | ||
| + | |- | ||
| + | |width="280" | 1/<i>f</i> noise | ||
| + | |width="220" | RF amplifiers | ||
| + | |width="220" | Pseudo-correlation and destriping | ||
| + | |width="140" | {{PlanckPapers|planck2013-p02a}} {{PlanckPapers|planck2014-a04||Planck-2015-A04}} | ||
| + | |- | ||
| + | |width="280" | Bias fluctuations | ||
| + | |width="220" | RF amplifiers, back-end electronics& | ||
| + | |width="220" | Pseudo-correlation and destriping | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Thermal fluctuations | ||
| + | |width="220" | 4-K, 20-K and 300-K thermal stages | ||
| + | |width="220" | Calibration, destriping | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | 1-Hz spikes | ||
| + | |width="220" | Back-end electronics | ||
| + | |width="220" | Template fitting and removal | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | !width="280" | Effects dependent on sky signal (T and P) | ||
| + | |width="220" | | ||
| + | |width="220" | | ||
| + | |width="140" | | ||
| + | |- | ||
| + | |width="280" | Main beam ellipticity | ||
| + | |width="220" | Main beams | ||
| + | |width="220" | Accounted for in window function | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Near sidelobes pickup | ||
| + | |width="220" | Optical response at angles 5° from the main beam | ||
| + | |width="220" | Masking of Galaxy and point sources | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Far sidelobes pickup | ||
| + | |width="220" | Main and sub-reflector spillovers | ||
| + | |width="220" | Model sidelobes removed from timelines | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Analogue-to-digital converter nonlinearity | ||
| + | |width="220" | Back-end analogue-to-digital converter | ||
| + | |width="220" | Template fitting and removal | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Imperfect photometric calibration | ||
| + | |width="220" | Sidelobe pickup, radiometer noise temperature changes and other non-idealities | ||
| + | |width="220" | Calibration using the 4-K reference load voltage output | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Pointing | ||
| + | |width="220" | Uncertainties in pointing reconstruction, thermal changes affecting focal plane geometry | ||
| + | |width="220" | Negligible impact anisotropy measurements | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | !width="280" | Effects specifically impacting polarization | ||
| + | |width="220" | | ||
| + | |width="220" | | ||
| + | |width="140" | | ||
| + | |- | ||
| + | |width="280" | Bandpass asymmetries | ||
| + | |width="220" | Differential orthomode transducer and receiver bandpass response | ||
| + | |width="220" | Spurious polarization removal | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Polarization angle uncertainty | ||
| + | |width="220" | Uncertainty in the polarization angle in-flight measurement | ||
| + | |width="220" | Negligible impact | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |width="280" | Orthomode transducer cross-polarization | ||
| + | |width="220" | Imperfect polarization separation | ||
| + | |width="220" | Negligible impact | ||
| + | |width="140" | {{PlanckPapers|planck2014-a03||Planck-2015-A03}} | ||
| + | |- | ||
| + | |} | ||
| + | |||
| + | The impact of 1/<i>f</i> noise has been assessed using half-ring noise maps normalized to the white noise estimate at each pixel (obtained from the white noise covariance matrix), so that a perfectly white noise map would be Gaussian and isotropic with unit variance. Deviations from unity trace the contribution of residual 1/<i>f</i> noise in the final maps, which ranges from 0.06% at 70 GHz to 2% at 30 GHz. | ||
| + | Pixel uncertainties due to other systematic effects have been calculated on simulated maps degraded to <i>N</i><sub>side</sub> = 128 at 30 and 44 GHz and <i>N</i><sub>side</sub> = 256 at 70 GHz, in order to approximate the optical beam size. This downgrading has been applied in all cases that a systematic effect has been evaluated at map level. | ||
| + | |||
| + | In Table 2 we list the rms and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as the "peak-to-peak" (p-p) difference, although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map. | ||
<center> | <center> | ||
| − | '''Table | + | <small>'''Table 2. Summary of systematic effects uncertainties on maps in μK<sub>CMB</sub> units.'''</small> |
| − | |||
</center> | </center> | ||
| − | + | {| border="0" cellspacing="0" cellpadding="2" align="center" | |
| − | + | |width="450"| <center>'''30 GHz'''</center> | |
| + | |- | ||
| + | |width="450"| [[File:Selection_263.png|450px]] | ||
| + | |- | ||
| + | |width="450"| <center>'''44 GHz'''</center> | ||
| + | |- | ||
| + | |width="450"| [[File:Selection_261.png|450px]] | ||
| + | |- | ||
| + | |width="450"| <center>'''70 GHz'''</center> | ||
| + | |- | ||
| + | |width="450"| [[File:Selection_262.png|450px]] | ||
| + | |} | ||
| − | + | Angular power spectra have been obtained from full resolution (<i>N</i><sub>side</sub> = 1024) systematic effect maps at each frequency using the HEALPix Anafast routine {{BibCite|gorski2005}}. In Fig. 1 we show the power spectrum of the various effects compared with the Planck best-fit spectra and with the noise level coming from the half-ring difference maps. | |
| − | |||
| − | |||
| + | Our assessment shows that the global impact of systematic effect uncertainties in the LFI do not limit either temperature or <i>E</i>-mode spectrum measurements. | ||
<center> | <center> | ||
| − | ''' | + | [[File:Selection_264.png|900px]] |
| − | + | ||
| + | [[File:Selection_265.png|900px]] | ||
| + | |||
| + | [[File:Selection_266.png|900px]] | ||
| + | |||
| + | <small>'''Figure 1. Angular power spectra of the various systematic effects compared to the Planck beam-filtered temperature and polarization spectra. The thick dark-grey curve represents the total contribution. The dark-green dotted curve represent the contribution from far sidelobes that has been removed from the data and, therefore not considered in the total. The CMB <i>TT</i> and <i>EE</i> curves correspond to the Planck best-fit power spectra. The theoretical <i>B</i>-mode CMB spectrum assumes a tensor-to-scalar ratio <i>r</i> = 0.1, a tensor spectral index <i>n</i><sub>T</sub>=0 and has not been beam-filtered. ''Rows'': 30, 44 and 70 GHz spectra. ''Columns'': temperature, <i>E</i>-mode and <i>B</i>-mode spectra. .'''</small> | ||
</center> | </center> | ||
| − | + | ==Detailed description of the various effects== | |
| − | + | A detailed description of the impact of the various effects is conained in the paper {{PlanckPapers|planck2014-a04||Planck-2015-A04}} and details will also be updated in this supplement. | |
| + | |||
| + | |||
| + | <!-- | ||
| + | |||
| + | A detailed description of the impact of the various effects is conained in the paper being prepared for the submission of a dedicated paper to A&A and will also appear in this supplement. We expect it to be available by the end of February. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Effects independent of sky signal== | ==Effects independent of sky signal== | ||
| − | ===Noise correlations and 1/f noise=== | + | ===Noise correlations and 1/<i>f</i> noise=== |
| − | + | TBW | |
| − | + | ||
| − | + | As described in Ref. {{BibCite|seiffert2002}} and {{PlanckPapers|planck2011-1-4}}, imperfect matching of components generates isolation between the complementary diodes of a receiver between −10 and −15 dB. This imperfect isolation leads to a small anti-correlated component in the white noise that is cancelled by a weighted average of the time-ordered data from the two diodes of each receiver as the first step of athe processing. This avoids the complication of tracking the anti-correlated white noise throughout the analysis. | |
| + | We treat the combined diode data as the raw data, and calibration, noise estimation, mapmaking etc. are performed on these combined data. The weights are determined from some initial estimates of the calibrated noise for each detector, and are kept fixed for the entire mission. | ||
| − | Over the course of the nominal mission, the noise is well fit by the model, with the exception of the early parts of | + | We estimate the signal-subtracted noise power spectrum of each receiver on 5-day time periods. Except for specific, mostly well understood events, shorter |
| + | timescale noise estimation does not produce any evident trends. For nearly all the radiometers our noise model is a very good approximation of the power spectrum. | ||
| + | |||
| + | Over the course of the nominal mission, the noise is well fit by the model, with the exception of the early parts of Survey 3. During this time, thermal instabilities brought on by the switchover from the nominal to the redundant sorption cooler cause poor fits and some changes in the parameters. | ||
===Thermal effects=== | ===Thermal effects=== | ||
| − | The LFI is susceptible to temperature fluctuations in the 300 K back-end modules, in the 4 K reference loads and in the 20 K focal plane. | + | TBW |
| + | |||
| + | The LFI is susceptible to temperature fluctuations in the 300-K back-end modules, in the 4-K reference loads and in the 20-K focal plane. | ||
| + | |||
| + | The temperature of 70-GHz reference loads was actively controlled by a proportional-integral-derivative (PID) system and is very stable (δ<i>T</i><sub>rms</sub> ∼ 0.13 mK). Reference loads of 30 and 44 GHz channels, instead, do not benefit from active thermal control. Their temperature is consequently more unstable and susceptible to major system-level events such as, for example, the switchover to the redundant sorption cooler. | ||
| − | + | The 20-K LFI focal plane temperature was measured by a sensor placed on the feedhorn flange of the LFI-28 receiver. The temperature during the first sky survey was very stable. Towards the end of the first year of operations the sorption cooler performance started to degrade and its stability was maintained with a series of controlled temperature changes. The switchover to the redundant cooler left a clear signature on all the main LFI temperatures. After this operation the level of temperature fluctuations on the focal plane increased unexpectedly, and this was later understood to be the effect of liquid hydrogen that was still present in the cold-end of the nominal cooler, because of the degraded compressor system not being able to absorb all the hydrogen that was present in the cooler line. Although this effect was later mitigated by a series of dedicated operations, most of the third sky survey suffered from a higher-than-nominal level of temperature variations. | |
| − | The | + | The temperature of the 300-K electronics box was measured by one of its temperature sensors. During the first sky survey the back-end temperature suffered from a 24-hour fluctuation caused by the satellite transponder that was switched on daily during contact with the ground station. After day 258 the system was left continuously on and the 24-hour modulation disappeared. This operation caused an increase of the absolute temperature level. The second temperature change that occurred corresponded to the sorption cooler switch-over operation. A yearly temperature modulation due to the satellite rotation around the Sun and a specific temperature spike need also to be considered. This was caused by an operational anomaly that caused the satellite to fail to repoint for an entire day, with a corresponding temperature increase of the warm units. |
| + | |||
| + | Details regarding the thermal stability performance of Planck can be found in {{PlanckPapers|planck2011-1-3}}, while the susceptibility of the LFI to temperature variations is discussed in Ref. {{BibCite|terenzi2009b}}. | ||
| − | |||
| − | |||
===Bias fluctuations=== | ===Bias fluctuations=== | ||
| − | The signal detected by the radiometers can vary because of fluctuations in the front-end and back-end | + | |
| − | * slow electric drifts, due to thermal changes in the power supply, in the RF amplifiers and in the detector diodes; | + | TBW |
| + | |||
| + | |||
| + | The signal detected by the radiometers can vary because of fluctuations in the front-end and back-end amplifier bias voltages. In the LFI these fluctuations occurred on two timescales: | ||
| + | * slow electric drifts, due to thermal changes in the power supply, in the RF amplifiers, and in the detector diodes; | ||
* fast and sudden electric instabilities, arising in the warm electronics or from electromagnetic interference effects, and affecting both the cold amplifiers and the warm detector diodes. | * fast and sudden electric instabilities, arising in the warm electronics or from electromagnetic interference effects, and affecting both the cold amplifiers and the warm detector diodes. | ||
| − | The effect of slow drifts is suppressed by the pseudo-correlation architecture of the differential radiometers. Fast electric changes produce quasi-random fluctuations and abrupt steep drops or jumps in the signal. If jumps are caused by instabilities in the front-end bias voltage then the effect involves the output voltage of both diodes in the radiometer. When the jumps occur in the back-end detector diodes (so-called “pop-corn noise”) they impact only the output voltage of the corresponding diode | + | The effect of slow drifts is suppressed by the pseudo-correlation architecture of the differential radiometers. Fast electric changes produce quasi-random fluctuations and abrupt steep drops or jumps in the signal. If jumps are caused by instabilities in the front-end bias voltage then the effect involves the output voltage of both diodes in the radiometer. When the jumps occur in the back-end detector diodes (so-called “pop-corn noise”) they impact only the output voltage of the corresponding diode, affecting sky and reference load samples. In both cases the differenced signal is largely immune from these effects. |
| + | |||
===1-Hz spikes=== | ===1-Hz spikes=== | ||
| − | + | ||
| + | TBW | ||
| + | |||
| + | An effect at 1 Hz is caused by pickup from the housekeeping electronics clock that occurs in the chain after the detector diodes and before the ADC converters {{PlanckPapers|planck2011-1-4}}{{BibCite|meinhold2009}}{{PlanckPapers|mennella2010}}. This spurious signal is detected in the radiometer time-domain outputs as a 1-s square wave with a rising edge near 0.5 s and a falling edge near 0.75 s in on-board time. In the frequency domain it appears at multiples of 1 Hz. | ||
Frequency spikes are present at some level in the output from all detectors, but affect the 44 GHz data most strongly because of the low voltage output and high post-detection gain values in that channel. For this reason spikes are removed from the 44 GHz time-ordered data via template fitting, as described in {{PlanckPapers|planck2013-p02}}. | Frequency spikes are present at some level in the output from all detectors, but affect the 44 GHz data most strongly because of the low voltage output and high post-detection gain values in that channel. For this reason spikes are removed from the 44 GHz time-ordered data via template fitting, as described in {{PlanckPapers|planck2013-p02}}. | ||
| + | |||
| + | |||
| + | ===Main beam ellipticity=== | ||
| + | TBW | ||
| + | |||
| + | ===Near sidelobe pickup=== | ||
| + | TBW | ||
==Effects dependent on sky signal== | ==Effects dependent on sky signal== | ||
===Sidelobe pick-up=== | ===Sidelobe pick-up=== | ||
| − | |||
| − | Straylight impacts the measured signal essentially in two ways: (i) through direct contamination and coupling with the main beam sky signal and (ii) in the photometric calibration of the radiometer detected signal. The impact on calibration and the adopted mitigation strategies are described in {{PlanckPapers|planck2013-p02b}}. | + | TBW |
| − | Because of the beam orientation, the straylight fingerprint is different in odd surveys compared to even surveys. The Galaxy, for example, is detected by the sub spillover in the odd surveys and by the main spillover in the even surveys. Because the sub spillover points approximately in the main beam direction, the Galaxy straylight pattern is close to the | + | |
| + | |||
| + | Straylight contamination arises from the spurious signal pickup from the telescope far sidelobes. The main sources of straylight contamination are the Galaxy, especially at 30 GHz, and the cosmological dipole, mainly detected in the directions of the main reflector and sub-reflector spillover. In principle we should also include the straylight contribution from the orbital dipole, but its effect is about a factor ten lower than the cosmic dipole so that it can safely be neglected in this framework (although it has been considered in the calibration pipeline). Further details about the Planck optical system are reported in {{PlanckPapers|tauber2010b}} and the LFI beam properties are provided in {{PlanckPapers|sandri2010}}. | ||
| + | |||
| + | Straylight impacts the measured signal essentially in two ways: (i) through direct contamination and coupling with the main beam sky signal; and (ii) in the photometric calibration of the radiometer detected signal. The impact on calibration and the adopted mitigation strategies are described in {{PlanckPapers|planck2013-p02b}}. | ||
| + | Because of the beam orientation, the straylight fingerprint is different in odd surveys compared to even surveys. The Galaxy, for example, is detected by the sub-reflector spillover in the odd surveys and by the main reflector spillover in the even surveys. Because the sub-reflector spillover points approximately in the main beam direction, the Galaxy straylight pattern is close to the Galactic plane. The main spillover, instead, points at about 85° from the main beam so that the Galaxy is re-imaged onto a ring. | ||
| + | |||
| + | |||
| + | ===ADC nonlinearity=== | ||
| + | |||
| + | TBW | ||
| − | |||
The linearity of analogue-to-digital converters (ADC) requires that the voltage step sizes between successive binary outputs are | The linearity of analogue-to-digital converters (ADC) requires that the voltage step sizes between successive binary outputs are | ||
| − | constant over the entire input dynamic range. If these steps are not constant we have a | + | constant over the entire input dynamic range. If these steps are not constant we have a nonlinearity in the ADC response that leads to calibration errors. |
| + | |||
| + | The typical fingerprint of ADC non linearity is a variation of the detector voltage output white noise that is not matched by a detectable variation in the voltage level. This effect was observed in the LFI radiometer data for the first time in flight, where drops of a few percent were observed in the voltage white noise, but not in the output level over, periods of few weeks. | ||
| + | The typical amplitude of the region where the nonlinearity occurs is of the order of 1 mV, corresponding to about three bits in the ADC. The ADC effect is strongest (3% to 6%) in the 44 GHz channels, because of their lower detector voltages. The ADC nonlinearity effect has been characterized from flight data and removed from the TOIs according to the procedure described in the main LFI data processing paper {{PlanckPapers|planck2013-p02}}. | ||
| + | |||
| − | |||
| − | |||
===Imperfect photometric calibration=== | ===Imperfect photometric calibration=== | ||
| − | |||
| − | * Incorrect assumptions regarding the calibration signal.In the case of LFI, the signal used for the calibration is the dipolar field caused by the motion of the Solar System with respect to the CMB rest frame and by the motion of the spacecraft around the Sun. We model the former using the values quoted by {{BibCite | + | |
| − | * Incorrect treatment of the calibration signal. To actually use any previous knowledge of the CMB dipole, we need to convolve the signal with the beam response of LFI radiometer. Any error in this step would produce a systematic effect in the map not only because of the | + | An important set of systematic effects are those related to the photometric calibration of the radiometers. Such effects are discussed at length in {{PlanckPapers|planck2013-p05}}. There are three different kinds of systematic effects that can affect the calibration. |
| − | * Incorrect reconstruction of gain fluctuations. Some of the algorithms | + | |
| + | * Incorrect assumptions regarding the calibration signal. In the case of LFI, the signal used for the calibration is the dipolar field caused by the motion of the Solar System with respect to the CMB rest frame and by the motion of the spacecraft around the Sun. We model the former using the values quoted by Ref. {{BibCite}} and the latter using the spacecraft’s attitude information. Any error in the numbers would directly lead to an error in the calibration of Planck-LFI data. | ||
| + | * Incorrect treatment of the calibration signal. To actually use any previous knowledge of the CMB dipole, we need to convolve the signal with the beam response of each LFI radiometer. Any error in this step would produce a systematic effect in the map, not only because of the incorrect shape expected for the calibration signal, but also because of the removal of the (wrong) dipole from the calibrated maps performed by the Planck-LFI pipeline {{PlanckPapers|planck2013-p02}}. Possible types of errors include: systematic errors in Planck’s dipole estimate; wrong convolution of the expected dipole with the radiometer beams; and incorrect masking of the Galaxy when fitting the observed signal with the dipole. | ||
| + | * Incorrect reconstruction of gain fluctuations. Some of the algorithms adopted in calibrating LFI data for this release use the radiometer equation and the recorded variations of the radiometer total-power output to track gain changes. In principle, any deviation in the behaviour of the radiometer from the ideal case (e.g., ADC nonlinearities) can therefore induce systematic effects in the gain curves. | ||
| + | |||
| + | |||
===Pointing effects=== | ===Pointing effects=== | ||
| − | |||
| − | |||
| − | |||
| + | TBW | ||
| + | |||
| + | |||
| + | Pointing uncertainties are translated into uncertainties in pixel temperature measurements. If pointing uncertainties are not constant in time then the statistics of the sky anisotropy measurements are not preserved, with a consequent impact on the power spectrum and cosmological parameters. In Planck-LFI pointing uncertainties arise from two distinct sources. | ||
| + | * Satellite pointing determination. The Planck Attitude Control Movement System guarantees a pointing accuracy of approximately 2′′ {{PlanckPapers|planck2013-p01}}, which is well within scientific requirements. However, small non-idealities in the system and errors in the attitude reconstruction caused, for example, by thermoelastic effects, can still affect the data. | ||
| + | * Uncertainties in the focal plane geometry reconstruction. The measurement of the LFI focal plane geometry is based on the determination of the beam pointing with respect to the nominal line of sight, exploiting observations of Jupiter. The peak of each beam was determined by fitting data with a bivariate Gaussian function, which may be not be precisely equivalent to the real beam centre. | ||
| + | |||
| + | |||
| + | |||
| + | ===Polarization angle uncertainty=== | ||
| + | TBW | ||
| + | |||
| + | ===Ortho-mode transducer cross-polarization=== | ||
| + | TBW | ||
| + | --> | ||
== References == | == References == | ||
Latest revision as of 13:28, 19 September 2016
Contents
Overview[edit]
Known systematic effects in the Planck-LFI data can be divided into two broad categories: effects independent of the sky signal, which can be considered as additive or multiplicative spurious contributions to the measured timelines, and effects which are dependent on the sky and that cannot be considered independently from the observation strategy.
Here we report a brief summary of these effects, all the details can be found in Planck-2013-III[1] and Planck-2015-A04[2].
Summary of uncertainties due to systematic effects[edit]
In this section we provide a top-level overview of the uncertainties due to systematic effects in the Planck-LFI CMB temperature maps and power spectra. Table 1 provides a list of these effects with short indications of their cause, strategies for removal and references to sections and/or papers where more information is found.
| Effect | Source | Control/Removal | Reference |
|---|---|---|---|
| Effects independent of sky signal (T and P) | |||
| White noise correlation | Phase-switch imbalance | Diode weighting | Planck-2013-III[1]Planck-2015-A04[2] |
| 1/f noise | RF amplifiers | Pseudo-correlation and destriping | Planck-2013-III[1]Planck-2015-A04[2] |
| Bias fluctuations | RF amplifiers, back-end electronics& | Pseudo-correlation and destriping | Planck-2015-A03[3] |
| Thermal fluctuations | 4-K, 20-K and 300-K thermal stages | Calibration, destriping | Planck-2015-A03[3] |
| 1-Hz spikes | Back-end electronics | Template fitting and removal | Planck-2015-A03[3] |
| Effects dependent on sky signal (T and P) | |||
| Main beam ellipticity | Main beams | Accounted for in window function | Planck-2015-A03[3] |
| Near sidelobes pickup | Optical response at angles 5° from the main beam | Masking of Galaxy and point sources | Planck-2015-A03[3] |
| Far sidelobes pickup | Main and sub-reflector spillovers | Model sidelobes removed from timelines | Planck-2015-A03[3] |
| Analogue-to-digital converter nonlinearity | Back-end analogue-to-digital converter | Template fitting and removal | Planck-2015-A03[3] |
| Imperfect photometric calibration | Sidelobe pickup, radiometer noise temperature changes and other non-idealities | Calibration using the 4-K reference load voltage output | Planck-2015-A03[3] |
| Pointing | Uncertainties in pointing reconstruction, thermal changes affecting focal plane geometry | Negligible impact anisotropy measurements | Planck-2015-A03[3] |
| Effects specifically impacting polarization | |||
| Bandpass asymmetries | Differential orthomode transducer and receiver bandpass response | Spurious polarization removal | Planck-2015-A03[3] |
| Polarization angle uncertainty | Uncertainty in the polarization angle in-flight measurement | Negligible impact | Planck-2015-A03[3] |
| Orthomode transducer cross-polarization | Imperfect polarization separation | Negligible impact | Planck-2015-A03[3] |
The impact of 1/f noise has been assessed using half-ring noise maps normalized to the white noise estimate at each pixel (obtained from the white noise covariance matrix), so that a perfectly white noise map would be Gaussian and isotropic with unit variance. Deviations from unity trace the contribution of residual 1/f noise in the final maps, which ranges from 0.06% at 70 GHz to 2% at 30 GHz. Pixel uncertainties due to other systematic effects have been calculated on simulated maps degraded to Nside = 128 at 30 and 44 GHz and Nside = 256 at 70 GHz, in order to approximate the optical beam size. This downgrading has been applied in all cases that a systematic effect has been evaluated at map level.
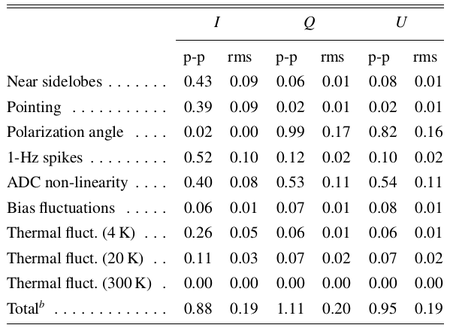
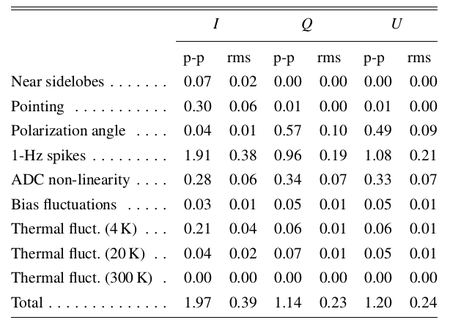
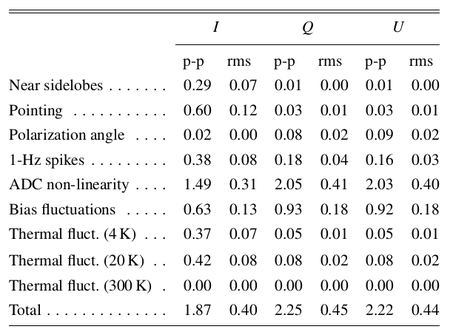
In Table 2 we list the rms and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as the "peak-to-peak" (p-p) difference, although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map.
Table 2. Summary of systematic effects uncertainties on maps in μKCMB units.
|
|
|
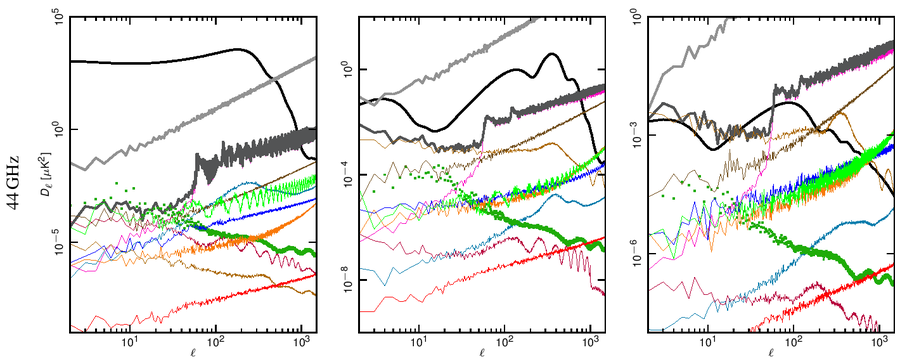
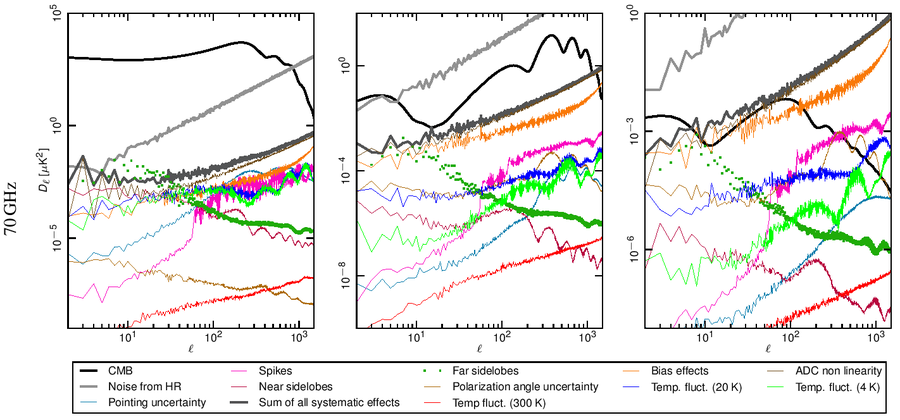
Angular power spectra have been obtained from full resolution (Nside = 1024) systematic effect maps at each frequency using the HEALPix Anafast routine [4]. In Fig. 1 we show the power spectrum of the various effects compared with the Planck best-fit spectra and with the noise level coming from the half-ring difference maps.
Our assessment shows that the global impact of systematic effect uncertainties in the LFI do not limit either temperature or E-mode spectrum measurements.
Figure 1. Angular power spectra of the various systematic effects compared to the Planck beam-filtered temperature and polarization spectra. The thick dark-grey curve represents the total contribution. The dark-green dotted curve represent the contribution from far sidelobes that has been removed from the data and, therefore not considered in the total. The CMB TT and EE curves correspond to the Planck best-fit power spectra. The theoretical B-mode CMB spectrum assumes a tensor-to-scalar ratio r = 0.1, a tensor spectral index nT=0 and has not been beam-filtered. Rows: 30, 44 and 70 GHz spectra. Columns: temperature, E-mode and B-mode spectra. .
Detailed description of the various effects[edit]
A detailed description of the impact of the various effects is conained in the paper Planck-2015-A04[2] and details will also be updated in this supplement.
References[edit]
- ↑ 1.01.11.2 Planck 2013 results. III. Low Frequency Instrument systematic uncertainties, Planck Collaboration, 2014, A&A, 571, A3
- ↑ 2.02.12.22.3 Planck 2015 results. III. LFI systematics, Planck Collaboration, 2016, A&A, 594, A3.
- ↑ 3.003.013.023.033.043.053.063.073.083.093.103.11 Planck 2015 results. II. LFI processing, Planck Collaboration, 2016, A&A, 594, A2.
- ↑ HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
(Planck) Low Frequency Instrument
Cosmic Microwave background
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).