Difference between revisions of "LFI systematic effect uncertainties"
| Line 108: | Line 108: | ||
In Table 2 we list the r.m.s. and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as peak-to-peak (p-p) difference although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map. | In Table 2 we list the r.m.s. and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as peak-to-peak (p-p) difference although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map. | ||
| − | |||
| − | |||
| − | + | <center> | |
| + | '''Table 2. Summary of systematic effects uncertainties on maps in μK<sub>CMB</sub>.''' | ||
| + | </center> | ||
| + | {| border="0" cellspacing="0" cellpadding="2" align="center" | ||
| + | |width="450"| <center>'''30 GHz'''</center> | ||
| + | |width="450"| <center>'''44 GHz'''</center> | ||
| + | |width="450"| <center>'''70 GHz'''</center> | ||
| + | |- | ||
| + | |width="450"| [[File:Selection_263.png|450px]] | ||
| + | |width="450"| [[File:Selection_261.png|450px]] | ||
| + | |width="450"| [[File:Selection_262.png|450px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
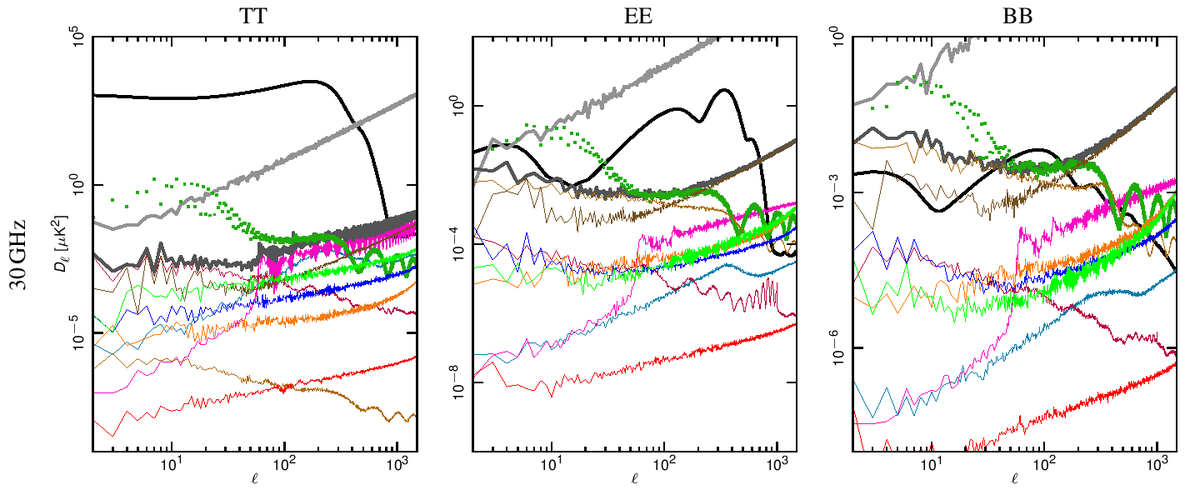
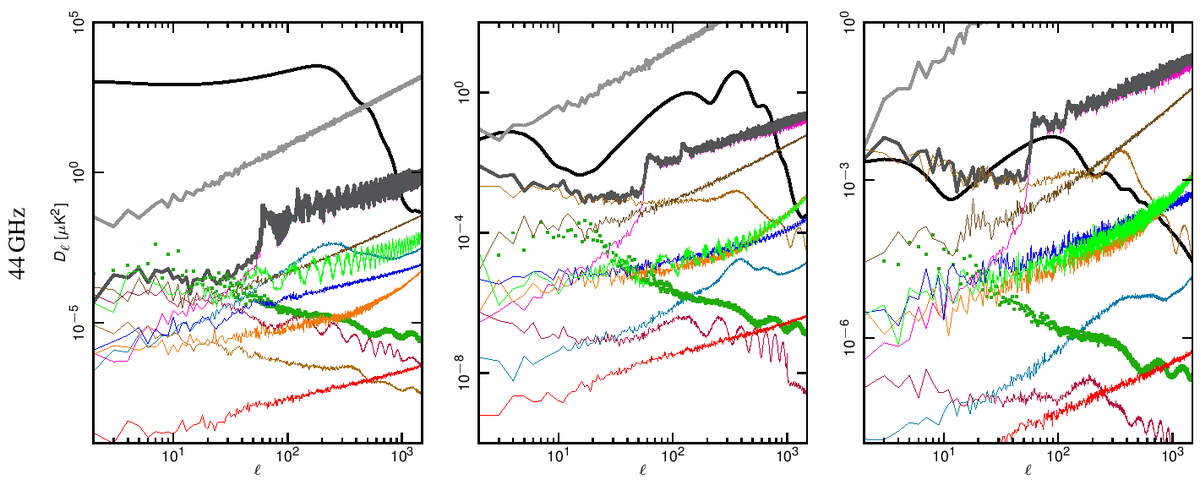
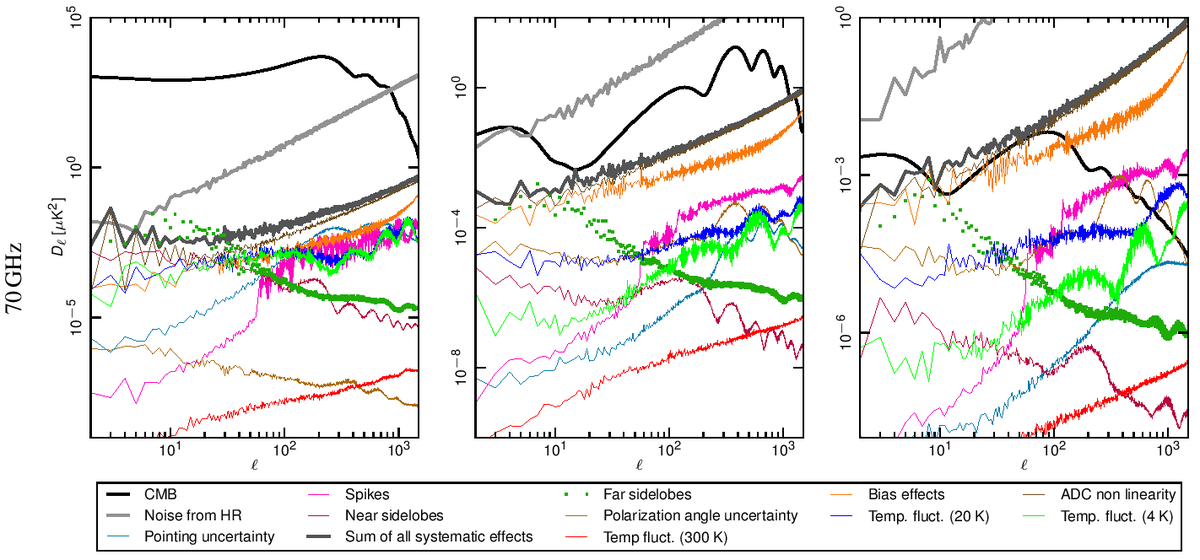
| − | Angular power spectra have been obtained from full resolution (N<sub>side</sub> = 1024) systematic effect maps at each frequency using HEALPix Anafast {{BibCite|gorski2005}} | + | Angular power spectra have been obtained from full resolution (N<sub>side</sub> = 1024) systematic effect maps at each frequency using HEALPix Anafast {{BibCite|gorski2005}}. In Fig. 1 we show how the power spectrum of the various effects compared with the Planck best-fit spectra and with the noise level coming from the half-ring difference maps. |
| + | |||
| + | Our assessment shows that the global impact of systematic effects uncertainties in the LFI do not limit either temperature or E-mode spectra measurements. | ||
| + | <center> | ||
| + | [[File:Selection_264.png|1200px]] | ||
| + | |||
| + | [[File:Selection_265.png|1200px]] | ||
| − | + | [[File:Selection_266.png|1200px]] | |
| − | + | '''Figure 1. Angular power spectra of the various systematic effects compared to the Planck beam-filtered temperature and polarization spectra. The dark-gray thick curve represents the total contribution. The dark-green dotted curve represent the contribution from far sidelobes that has been removed from the data and, therefore not considered in the total. The CMB TT and EE curves correspond to the Planck best-fit power spectra. The theoretical $B$-mode CMB spectrum assumes a tensor-to-scalar ratio r = 0.1, a tensor spectral index nT=0 and has not been beam-filtered. ''Rows'': 30, 44 and 70 GHz spectra. ''Columns'': temperature, E-mode and B-mode spectra. .''' | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | '''Figure 1. | ||
</center> | </center> | ||
| + | |||
| + | |||
==Effects independent of sky signal== | ==Effects independent of sky signal== | ||
===Noise correlations and 1/f noise=== | ===Noise correlations and 1/f noise=== | ||
| + | TBW | ||
| + | |||
| + | <!-- | ||
As described in {{BibCite|seiffert2002}}{{PlanckPapers|planck2011-1-4}} imperfect matching of components generates isolation between the complementary diodes of a receiver between −10 and −15 dB. This imperfect isolation leads to a small anti correlated component in the white noise that is cancelled by a weighted average of the time ordered data from the two diodes of each receiver as the first step of analysis. This avoids the complication of tracking the anti correlated white noise throughout the analysis. | As described in {{BibCite|seiffert2002}}{{PlanckPapers|planck2011-1-4}} imperfect matching of components generates isolation between the complementary diodes of a receiver between −10 and −15 dB. This imperfect isolation leads to a small anti correlated component in the white noise that is cancelled by a weighted average of the time ordered data from the two diodes of each receiver as the first step of analysis. This avoids the complication of tracking the anti correlated white noise throughout the analysis. | ||
We treat the combined diode data as the raw data, and calibration, noise estimation, map making etc. are performed on these combined data. The weights were determined from some initial estimates of the calibrated noise for each detector, and are kept fixed for the entire mission. | We treat the combined diode data as the raw data, and calibration, noise estimation, map making etc. are performed on these combined data. The weights were determined from some initial estimates of the calibrated noise for each detector, and are kept fixed for the entire mission. | ||
| Line 153: | Line 150: | ||
Over the course of the nominal mission, the noise is well fit by the model, with the exception of the early parts of sky survey 3. During this time, thermal instabilities brought on by the switchover from the nominal to the redundant sorption cooler cause poor fits and some changes in the parameters. | Over the course of the nominal mission, the noise is well fit by the model, with the exception of the early parts of sky survey 3. During this time, thermal instabilities brought on by the switchover from the nominal to the redundant sorption cooler cause poor fits and some changes in the parameters. | ||
| + | --> | ||
| + | ===Thermal effects=== | ||
| + | |||
| + | TBW | ||
| − | + | <!-- | |
The LFI is susceptible to temperature fluctuations in the 300 K back-end modules, in the 4 K reference loads and in the 20 K focal plane. | The LFI is susceptible to temperature fluctuations in the 300 K back-end modules, in the 4 K reference loads and in the 20 K focal plane. | ||
| Line 165: | Line 166: | ||
Details about the thermal stability performance of Planck can be found in {{PlanckPapers|planck2011-1-3}}, while the susceptibility of the LFI to temperature variations is discussed in {{BibCite|terenzi2009b}}. | Details about the thermal stability performance of Planck can be found in {{PlanckPapers|planck2011-1-3}}, while the susceptibility of the LFI to temperature variations is discussed in {{BibCite|terenzi2009b}}. | ||
| + | |||
| + | --> | ||
===Bias fluctuations=== | ===Bias fluctuations=== | ||
| + | |||
| + | TBW | ||
| + | |||
| + | <!-- | ||
| + | |||
The signal detected by the radiometers can vary because of fluctuations in the front-end and back-end amplifiers bias voltages. In the LFI these fluctuations occurred according to two time scales: | The signal detected by the radiometers can vary because of fluctuations in the front-end and back-end amplifiers bias voltages. In the LFI these fluctuations occurred according to two time scales: | ||
* slow electric drifts, due to thermal changes in the power supply, in the RF amplifiers and in the detector diodes; | * slow electric drifts, due to thermal changes in the power supply, in the RF amplifiers and in the detector diodes; | ||
| Line 172: | Line 180: | ||
The effect of slow drifts is suppressed by the pseudo-correlation architecture of the differential radiometers. Fast electric changes produce quasi-random fluctuations and abrupt steep drops or jumps in the signal. If jumps are caused by instabilities in the front-end bias voltage then the effect involves the output voltage of both diodes in the radiometer. When the jumps occur in the back-end detector diodes (so-called “pop-corn noise”) they impact only the output voltage of the corresponding diode and affect sky and reference load samples. In both cases the differenced signal is largely immune from these effects. | The effect of slow drifts is suppressed by the pseudo-correlation architecture of the differential radiometers. Fast electric changes produce quasi-random fluctuations and abrupt steep drops or jumps in the signal. If jumps are caused by instabilities in the front-end bias voltage then the effect involves the output voltage of both diodes in the radiometer. When the jumps occur in the back-end detector diodes (so-called “pop-corn noise”) they impact only the output voltage of the corresponding diode and affect sky and reference load samples. In both cases the differenced signal is largely immune from these effects. | ||
| + | |||
| + | --> | ||
===1-Hz spikes=== | ===1-Hz spikes=== | ||
| + | |||
| + | TBW | ||
| + | |||
| + | <!-- | ||
| + | |||
This effect is caused by pickup from the housekeeping electronics clock that occurs after the detector diodes and before the ADC converters {{PlanckPapers|planck2011-1-4}}{{BibCite|meinhold2009}}{{PlanckPapers|mennella2010}}. This spurious signal is detected in the radiometer time-domain outputs as a one second square wave with a rising edge near 0.5 s and a falling edge near 0.75 s in on-board time. In the frequency domain it appears at multiples of 1 Hz. | This effect is caused by pickup from the housekeeping electronics clock that occurs after the detector diodes and before the ADC converters {{PlanckPapers|planck2011-1-4}}{{BibCite|meinhold2009}}{{PlanckPapers|mennella2010}}. This spurious signal is detected in the radiometer time-domain outputs as a one second square wave with a rising edge near 0.5 s and a falling edge near 0.75 s in on-board time. In the frequency domain it appears at multiples of 1 Hz. | ||
Frequency spikes are present at some level in the output from all detectors, but affect the 44 GHz data most strongly because of the low voltage output and high post-detection gain values in that channel. For this reason spikes are removed from the 44 GHz time-ordered data via template fitting, as described in {{PlanckPapers|planck2013-p02}}. | Frequency spikes are present at some level in the output from all detectors, but affect the 44 GHz data most strongly because of the low voltage output and high post-detection gain values in that channel. For this reason spikes are removed from the 44 GHz time-ordered data via template fitting, as described in {{PlanckPapers|planck2013-p02}}. | ||
| + | |||
| + | --> | ||
===Main Beam Ellipticity=== | ===Main Beam Ellipticity=== | ||
TBW | TBW | ||
| − | === | + | ===Near Sidelobes pickup=== |
TBW | TBW | ||
==Effects dependent on sky signal== | ==Effects dependent on sky signal== | ||
===Sidelobe pick-up=== | ===Sidelobe pick-up=== | ||
| + | |||
| + | TBW | ||
| + | |||
| + | <!-- | ||
| + | |||
Straylight contamination arise from the spurious signal pickup from the telescope far sidelobes. Main sources of straylight contamination are the Galaxy, especially at 30 GHz, and the cosmological dipole, mainly detected in the directions of the main and sub reflectors spillover. In principle we should also include the straylight contribution from the orbital dipole, but its effect is of a factor ten lower than the cosmic dipole so that it can safely be neglected in this framework (but it has been considered in the calibration pipeline). Further details about the Planck optical system are reported in {{PlanckPapers|tauber2010b}} and the LFI beam properties are provided in {{PlanckPapers|sandri2010}}. | Straylight contamination arise from the spurious signal pickup from the telescope far sidelobes. Main sources of straylight contamination are the Galaxy, especially at 30 GHz, and the cosmological dipole, mainly detected in the directions of the main and sub reflectors spillover. In principle we should also include the straylight contribution from the orbital dipole, but its effect is of a factor ten lower than the cosmic dipole so that it can safely be neglected in this framework (but it has been considered in the calibration pipeline). Further details about the Planck optical system are reported in {{PlanckPapers|tauber2010b}} and the LFI beam properties are provided in {{PlanckPapers|sandri2010}}. | ||
Straylight impacts the measured signal essentially in two ways: (i) through direct contamination and coupling with the main beam sky signal and (ii) in the photometric calibration of the radiometer detected signal. The impact on calibration and the adopted mitigation strategies are described in {{PlanckPapers|planck2013-p02b}}. | Straylight impacts the measured signal essentially in two ways: (i) through direct contamination and coupling with the main beam sky signal and (ii) in the photometric calibration of the radiometer detected signal. The impact on calibration and the adopted mitigation strategies are described in {{PlanckPapers|planck2013-p02b}}. | ||
Because of the beam orientation, the straylight fingerprint is different in odd surveys compared to even surveys. The Galaxy, for example, is detected by the sub spillover in the odd surveys and by the main spillover in the even surveys. Because the sub spillover points approximately in the main beam direction, the Galaxy straylight pattern is close to the galactic plane. The main spillover, instead, points at about 85 degrees from the main beam so that the Galaxy is re-imaged onto a ring. | Because of the beam orientation, the straylight fingerprint is different in odd surveys compared to even surveys. The Galaxy, for example, is detected by the sub spillover in the odd surveys and by the main spillover in the even surveys. Because the sub spillover points approximately in the main beam direction, the Galaxy straylight pattern is close to the galactic plane. The main spillover, instead, points at about 85 degrees from the main beam so that the Galaxy is re-imaged onto a ring. | ||
| + | |||
| + | --> | ||
===ADC non linearity=== | ===ADC non linearity=== | ||
| + | |||
| + | TBW | ||
| + | |||
| + | <!-- | ||
| + | |||
The linearity of analogue-to-digital converters (ADC) requires that the voltage step sizes between successive binary outputs are | The linearity of analogue-to-digital converters (ADC) requires that the voltage step sizes between successive binary outputs are | ||
constant over the entire input dynamic range. If these steps are not constant we have a non linearity in the ADC response that leads to calibration errors. | constant over the entire input dynamic range. If these steps are not constant we have a non linearity in the ADC response that leads to calibration errors. | ||
| Line 196: | Line 225: | ||
The typical fingerprint of ADC non linearity is a variation of the detector voltage output white noise not paired by a detectable variation in the voltage level. This effect was observed in the LFI radiometer data for the first time in flight, where drops of few percent were observed in the voltage white noise but not in the output level over periods of few weeks. | The typical fingerprint of ADC non linearity is a variation of the detector voltage output white noise not paired by a detectable variation in the voltage level. This effect was observed in the LFI radiometer data for the first time in flight, where drops of few percent were observed in the voltage white noise but not in the output level over periods of few weeks. | ||
The typical amplitude of the region where the non linearity occurs is of the order of 1 mV, corresponding to about three bits in the ADC. The ADC effect is strongest (3 to 6%) in the 44 GHz channels, because of their lower detector voltages. The ADC non linearity effect has been characterised from flight data and removed from the TOIs according to the procedure described in the main LFI data processing paper {{PlanckPapers|planck2013-p02}}. | The typical amplitude of the region where the non linearity occurs is of the order of 1 mV, corresponding to about three bits in the ADC. The ADC effect is strongest (3 to 6%) in the 44 GHz channels, because of their lower detector voltages. The ADC non linearity effect has been characterised from flight data and removed from the TOIs according to the procedure described in the main LFI data processing paper {{PlanckPapers|planck2013-p02}}. | ||
| + | |||
| + | --> | ||
===Imperfect photometric calibration=== | ===Imperfect photometric calibration=== | ||
| + | |||
| + | <!-- | ||
| + | |||
An important set of systematic effects are those related with the photometric calibration of the radiometers. Such effects are discussed at length by {{PlanckPapers|planck2013-p05}}. There are three different kinds of systematic effects that can affect the calibration. | An important set of systematic effects are those related with the photometric calibration of the radiometers. Such effects are discussed at length by {{PlanckPapers|planck2013-p05}}. There are three different kinds of systematic effects that can affect the calibration. | ||
| Line 203: | Line 237: | ||
* Incorrect treatment of the calibration signal. To actually use any previous knowledge of the CMB dipole, we need to convolve the signal with the beam response of LFI radiometer. Any error in this step would produce a systematic effect in the map not only because of the wrong shape expected for the calibration signal, but also because of the removal of the (wrong) dipole from the calibrated maps done by the Planck-LFI pipeline {{PlanckPapers|planck2013-p02}}. Possible types of errors include: systematic errors in Planck’s dipole estimate, wrong convolution of the expected dipole with the radiometer beams, uncorrect masking of the Galaxy when fitting the observed signal with the dipole, etc. | * Incorrect treatment of the calibration signal. To actually use any previous knowledge of the CMB dipole, we need to convolve the signal with the beam response of LFI radiometer. Any error in this step would produce a systematic effect in the map not only because of the wrong shape expected for the calibration signal, but also because of the removal of the (wrong) dipole from the calibrated maps done by the Planck-LFI pipeline {{PlanckPapers|planck2013-p02}}. Possible types of errors include: systematic errors in Planck’s dipole estimate, wrong convolution of the expected dipole with the radiometer beams, uncorrect masking of the Galaxy when fitting the observed signal with the dipole, etc. | ||
* Incorrect reconstruction of gain fluctuations. Some of the algorithms we used in calibrating LFI data for this release use the radiometer equation and the recorded variations of the radiometers total-power output to track gain changes. In principle, any deviation in the behaviour of the radiometer from the ideal case (e.g., ADC non linearities) can therefore induce systematic effects in the gain curves. | * Incorrect reconstruction of gain fluctuations. Some of the algorithms we used in calibrating LFI data for this release use the radiometer equation and the recorded variations of the radiometers total-power output to track gain changes. In principle, any deviation in the behaviour of the radiometer from the ideal case (e.g., ADC non linearities) can therefore induce systematic effects in the gain curves. | ||
| + | |||
| + | --> | ||
===Pointing effects=== | ===Pointing effects=== | ||
| + | |||
| + | TBW | ||
| + | |||
| + | <!-- | ||
| + | |||
Pointing uncertainties are translated into uncertainties in pixel temperature measurements. If pointing uncertainties are not constant in time then the statistics of the sky anisotropy measurements is not preserved with a consequent impact on power spectrum and cosmological parameters. In Planck-LFI pointing uncertainties arise from: | Pointing uncertainties are translated into uncertainties in pixel temperature measurements. If pointing uncertainties are not constant in time then the statistics of the sky anisotropy measurements is not preserved with a consequent impact on power spectrum and cosmological parameters. In Planck-LFI pointing uncertainties arise from: | ||
* Satellite pointing determination. The Planck Attitude Control Movement System guarantees a pointing accuracy of ∼ 2′′ {{PlanckPapers|planck2013-p01}}, which is well within scientific requirements. However, small non idealities in the system and errors in the attitude reconstruction caused, for example, by thermoelastic effects, can affect the data. | * Satellite pointing determination. The Planck Attitude Control Movement System guarantees a pointing accuracy of ∼ 2′′ {{PlanckPapers|planck2013-p01}}, which is well within scientific requirements. However, small non idealities in the system and errors in the attitude reconstruction caused, for example, by thermoelastic effects, can affect the data. | ||
* Uncertainties in the focal plane geometry reconstruction. The measurement of Planck-LFI focal plane geometry is based on the determination of the beam pointing with respect to the nominal line of sight exploiting Jupiter observation. The peak of each beam has been determined by fitting data with a bivariate gaussian function which may be not representative of the real beam centre. | * Uncertainties in the focal plane geometry reconstruction. The measurement of Planck-LFI focal plane geometry is based on the determination of the beam pointing with respect to the nominal line of sight exploiting Jupiter observation. The peak of each beam has been determined by fitting data with a bivariate gaussian function which may be not representative of the real beam centre. | ||
| + | |||
| + | --> | ||
===Polarization Angle Uncertainty=== | ===Polarization Angle Uncertainty=== | ||
Revision as of 09:29, 30 January 2015
Contents
Overview[edit]
Known systematic effects in the Planck-LFI data can be divided into two broad categories: effects independent of the sky signal, which can be considered as additive or multiplicative spurious contributions to the measured timelines, and effects which are dependent on the sky and that cannot be considered independently from the observation strategy.
Here we report a brief summary of these effects, all the details can be found in Planck-2013-III[1].
Summary of uncertainties due to systematic effects[edit]
In this section we provide a top-level overview of the uncertainties due to systematic effects in the Planck-LFI CMB temperature maps and power spectra. Table 1 provides a list of these effects with short indications of their cause, strategies for removal and references to sections and/or papers where more information is found.
| Effect | Source | Control/Removal | Reference |
|---|---|---|---|
| Effects independent of sky signal (T and P) | |||
| White noise correlation | Phase switch imbalance | Diode weighting | Planck-2013-III[1] |
| 1/ noise | RF amplifiers | Pseudo-correlation and destriping | Planck-2013-III[1] |
| Bias fluctuations | RF amplifiers, back-end electronics& | Pseudo-correlation and destriping | DPC paper |
| Thermal fluctuations | 4 K, 20 K and 300 K thermal stages | Calibration, destriping | DPC paper |
| 1 Hz spikes | Back-end electronics | Template fitting and removal | DPC paper |
| Effects dependent on sky signal (T and P) | |||
| Main beam ellipticity | Main beams | Accounted for in window function | DPC paper |
| Near sidelobes pickup | Optical response at angles from the main beam | Masking of Galaxy and point sources | DPC paper |
| Far sidelobes pickup | Main and sub-reflector spillovers | Model sidelobes removed from timelines | DPC paper |
| Analogue-to-digital converter non linearity | Back-end analogue-to-digital converter | Template fitting and removal | DPC paper |
| Imperfect photometric calibration | Sidelobe pickup, radiometer noise temperature changes and other non-idealities | Calibration using the 4 K reference load voltage output | DPC paper |
| Pointing | Uncertainties in pointing reconstruction, thermal changes affecting focal plane geometry | Negligible impact anisotropy measurements | DPC paper |
| Effects specifically impacting polarization | |||
| Bandpass asymmetries | Differential orthomode transducer and receiver bandpass response | Spurious polarisation removal | DPC paper |
| Polarization angle uncertainty | Uncertainty in the polarization angle in-flight measurement | Negligible impact | DPC paper |
| Orthomode transducer cross-polarization | Imperfect polarization separation | Negligible impact | DPC paper |
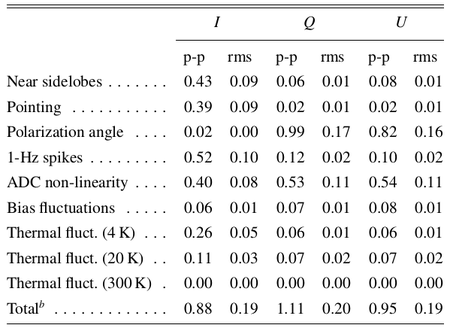
The impact of 1/ noise has been assessed using half-ring noise maps normalised to the white noise estimate at each pixel obtained from the white noise covariance matrix, so that a perfectly white noise map would be Gaussian and isotropic with unit variance. Deviations from unity trace the contribution of residual 1/f noise in the final maps, which ranges from 0.06% at 70 GHz to 2% at 30 GHz. Pixel uncertainties due to other systematic effects have been calculated on simulated maps degraded at Nside = 128 at 30 and 44 GHz and Nside = 256 at 70 GHz in order to approximate the optical beam size. This downgrading has been applied in all cases a systematic effect has been evaluated at map level.
In Table 2 we list the r.m.s. and the difference between the 99% and the 1% quantities in the pixel value distributions. For simplicity we refer to this difference as peak-to-peak (p-p) difference although it neglects outliers but effectively approximates the peak-to-peak variation of the effect on the map.
Table 2. Summary of systematic effects uncertainties on maps in μKCMB.
|
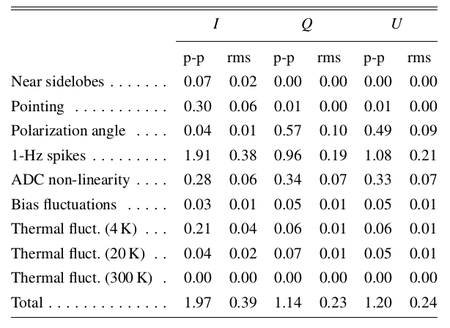
|
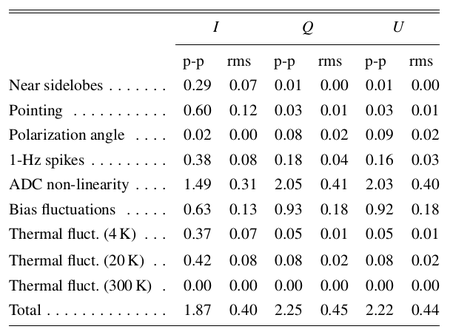
|
Angular power spectra have been obtained from full resolution (Nside = 1024) systematic effect maps at each frequency using HEALPix Anafast [2]. In Fig. 1 we show how the power spectrum of the various effects compared with the Planck best-fit spectra and with the noise level coming from the half-ring difference maps.
Our assessment shows that the global impact of systematic effects uncertainties in the LFI do not limit either temperature or E-mode spectra measurements.
Figure 1. Angular power spectra of the various systematic effects compared to the Planck beam-filtered temperature and polarization spectra. The dark-gray thick curve represents the total contribution. The dark-green dotted curve represent the contribution from far sidelobes that has been removed from the data and, therefore not considered in the total. The CMB TT and EE curves correspond to the Planck best-fit power spectra. The theoretical $B$-mode CMB spectrum assumes a tensor-to-scalar ratio r = 0.1, a tensor spectral index nT=0 and has not been beam-filtered. Rows: 30, 44 and 70 GHz spectra. Columns: temperature, E-mode and B-mode spectra. .
Effects independent of sky signal[edit]
Noise correlations and 1/f noise[edit]
TBW
Thermal effects[edit]
TBW
Bias fluctuations[edit]
TBW
1-Hz spikes[edit]
TBW
Main Beam Ellipticity[edit]
TBW
Near Sidelobes pickup[edit]
TBW
Effects dependent on sky signal[edit]
Sidelobe pick-up[edit]
TBW
ADC non linearity[edit]
TBW
Imperfect photometric calibration[edit]
Pointing effects[edit]
TBW
Polarization Angle Uncertainty[edit]
TBW
Ortho-Mode Transducer Cross-Polarization[edit]
TBW
References[edit]
- ↑ 1.01.11.2 Planck 2013 results. III. Low Frequency Instrument systematic uncertainties, Planck Collaboration, 2014, A&A, 571, A3
- ↑ HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
(Planck) Low Frequency Instrument
Cosmic Microwave background
Data Processing Center
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
analog to digital converter