Detector pointing
Contents
Introduction and Summary[edit]
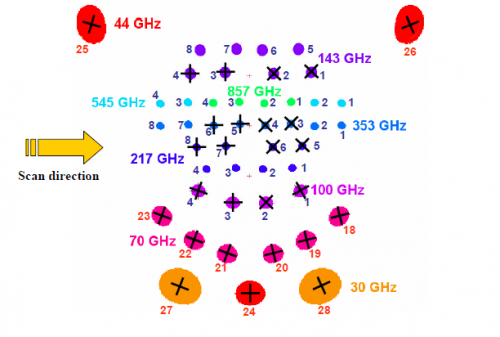
The overall geometry of the Planck focal plane is shown here:
In order to take full advantage of the Planck beams, we must know the individual detector positions to a precision of better than several arcseconds, over the course of the entire mission.
Spacecraft pointing comes from the on-board star tracker at 8 Hz between repointings (Attitude History File, AHF). This is translated via a series of three-dimensional rotations to a pointing for the centre of the focal plane and resampled to the HFI or LFI TOI data rate for convenience after correcting for the wobble angle (see below). We must then further rotate this focal-plane boresight pointing to the individual detector locations. Because neither the rotations from the star tracker to the boresight nor those from the boresight to the individual detectors are known exactly a priori, we must calibrate using flight data.
Specifically, measurements of HFI and LFI Detector pointing are based largely on observations of the brighter planets, with information from the much more frequent observation of lower-flux galactic and extragalactic high-frequency sources used to monitor and build a model of overall pointing drift. This long-term drift of the spacecraft attitude is due to changes in the moment of inertia of the spacecraft, and includes specific events which may induce sudden changes, essentially random as far as our ability to predict the effects thereof. In this delivery HFI used a model (described below) to follow the pointing drift continuously, while LFI uses two different focal plane description for the two time periods separated by operations perfomed on the instrument that modify the termal behaviour. The two approach are consistent to better than a few arcsec.
Note that for HFI the resulting pointing model cannot easily be directly compared to a physical/optical model: in particular, it includes a phase shift in the scan direction from the convolution and deconvolution of the detector transfer function, which is complex in the Fourier domain (see Planck-2013-VII[1]). This phase shift was not measured during normal operations, but a short campaign during which the spacecraft was spun at a higher rate will be used to determine these offsets in future date releases. Comparison with the initial optical model indicates that the in-scan change due to this phase shift is of the order of 1 arcminute. Note also that aberration is corrected in all observations.
The final pointing model is measured to be better than 2 arcsecond rms in the co-scan and cross-scan directions averaged over ten-day periods, as shown below. Note that there are larger hourly drifts of up to 10 arcseconds due to interference from the radiometer electronics box assembly (REBA) as discussed more fully in Planck-2013-VI[2].
Wobble Angle[edit]
The wobble angle is the angle between the Principal Axis Reference Frame and the Body Reference Frame of Planck, both of which have their origin in the Planck Baricenter (ACMS, AHF-ICD). It is normally decomposed into its three components .
Pointings are determined by a set of rotations converting coordinates in the STR (Star Tracker) reference frame to ECL (Ecliptic) reference frame, i.e. defining the rotation matrix . The matrix can be decomposend in a sequence of matrix mutiplications:
here we used to denote transformation from Rerference Frame RFA to Reference Frame RFB, and .
The converts from STR coordinates to Body Reference Frame coordinates, it is a constant matrix.
where is the STR boresight angle assumed to be constant and aligned with the telescope LOS, but this is not the case. The STR is located on the SVM, at about 1.5 m from the origin of the Body reference frame, a change in its position of 0.15 mm will result in a change of its orientation of about radiants about 20 arcsec.
There is no way to measure directly those changes. So the effect is that to have an apparent change in the , (tilt angles as defined in the AHF) and (azimuth angle as defined in the AHF) angles: the reason is apparent immediately when looking at the way a perturbation in STR reference frame orientation propagates.
AHF provides wobble angle measures at 1 minute (, ) and one OD () rate. Indeed is provided at each pointing period but measures within each given OD are constant.
Assuming to have quaternions represented by rotation matrix at a time , and assuming to have representative values of true wobble angles , , and a way to estimate the apparent , , it is possible to remove the apparent effect.
With the available information it can be done for and .
The correction algorithm initializes two rotation matrices as references using and from the first pointing period of the nominal mission:
Then, for each pointing period, builds two correction matrices using and as provided by the AHF in the Observation section:
From these matrices the correction matrix is build:
Each quaternion of the AHF is finally corrected using .
Stellar Aberration[edit]
The corrected quaternions are interpolated using Spherical Linear Interpolation algorithm and transformed in cartesian vector, which we call . For each sample the stellar aberration correction is applied:
where is the satellite velocity and is the speed of light. After this operation the vector is normalized.
Finally the cartesian vetor is converted in Ecliptic Coordinates, the detector pointing.
Beam Rotation[edit]
The rotation of the beam with respect to North is the angle and is computed rotating the corrected quaternions using:
The resulting rotation matrix represents the rotation of the beam, the angle is then:
Initial measurements: Mars 1 and other planets[edit]
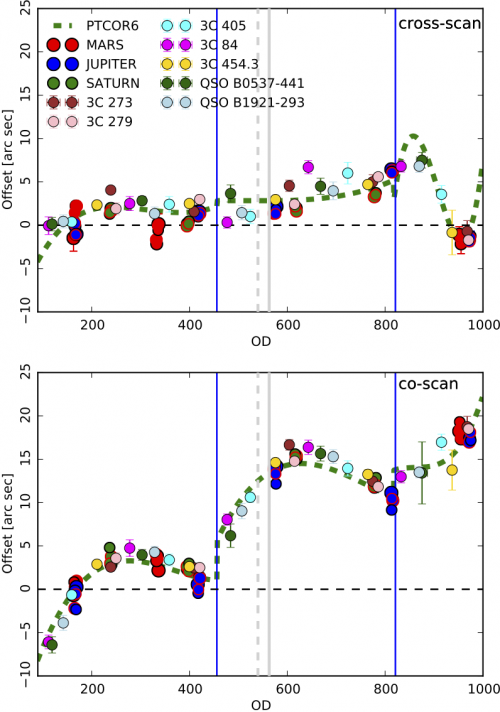
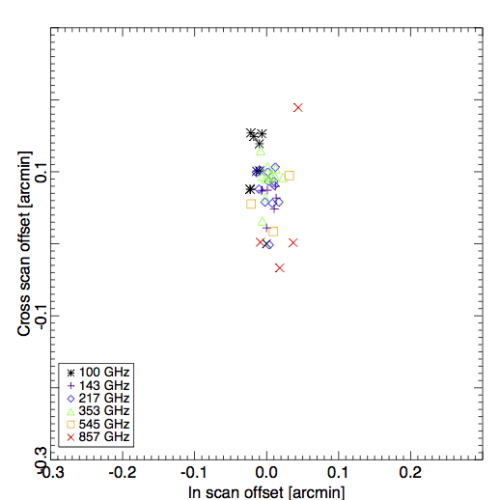
The first observation of Mars, which occured around 180 days from launch, is the baseline against which other objects are compared. Here, we show the relative pointing of Mars 1 to the pre-launch RFFM.
Focal plane drift: map-based measurement of detector positions[edit]
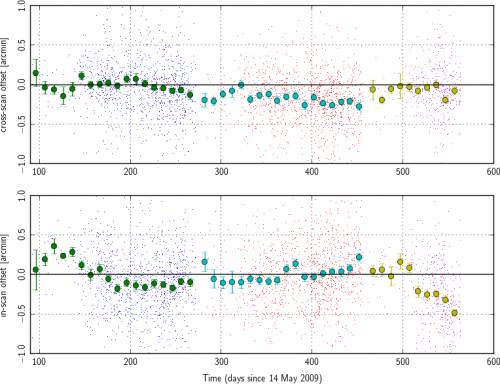
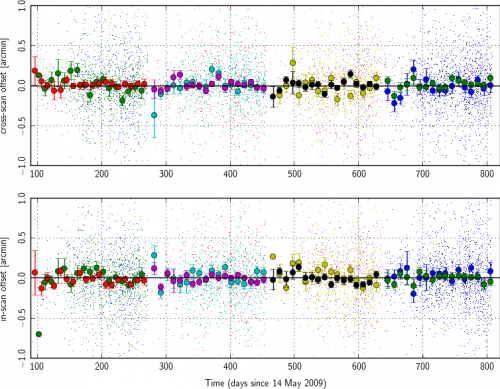
Prior to modeling of systematic changes in the Planck pointing, we find secular drifts of order one arcminute over the course of the nominal mission. We monitor this by making point-source catalogs based on single Planck surveys, only counting those objects which are observed over the course of less than seven days (this limits us to observations away from the ecliptic poles where Planck's observing strategy is highly cross-linked). We cross-match these catalog positions to the known IRAS point-source catalog[3] and average the deviations in ten-day blocks (the individual measurements are shown as lighter points; error bars assume equal weighting for all points, but the results are not sensitive to any imposed S/N cutoff):
An analysis performed directly in the timestream gives similar results, below (evaluated until the end of HFI operations in January 2012).
A model for Planck HFI Pointing[edit]
These analyses allow us to build a model for the pointing drift. The following describes the procedures used for the HFI detectors.
The correction is based on the measurement of pointing offset directly from the timeline, on a small sample of known and bright radio sources and planets. First the beam shape of each detector is measured by stacking individual timeline observation of bright planets. This process is of course contaminated by pointing error, but this is reduced by allowing each pass on the planet to be slightly displaced in order to correct for the observed location of the planet. This process yields a very clean estimate of the beam of each detector.
Those beams are then used to determine the offset of the observed location of the planets (Mars, Saturn, and Jupiter) and of a few (~10) bright radio sources. These offsets are estimated using detectors at all frequencies for the planets, and only at 100GHz, 143GHz and 217GHz for the radio sources.
From the planet observations, one can recover the alignment of each detector in the focal plane, as well as a first pointing correction measured at the times of individual planet crossings. This pointing correction is obtained by fitting splines on the planet observation from each detector. We further allow this correction to have a sharp jump between the second and third survey (the time of the SCS switchover on OD 455).
This first pointing correction is further refined (at the lower HFI frequencies only) using the point sources observations in order to fill the period between planet observations. The radio source offsets require further treatment than the planet based offsets. First, the brightness of the sources being much smaller than planets, the offset on individual detector observation are very noisy, and we filter out the noise by building median offsets for each point source observation. Second, since the sources can be slightly extended we still observe systematic offset above and below the planet based pointing correction in a regular alternating pattern. This is due to the fact that we are observing those extended objects scanning in alternating directions, and our fit of those extended sources to our beam translate into this systematic alternating pattern. We thus allow for a small, arcsec correction of those offsets: i.e., each object is allowed a single offset displacement of order arc seconds in order to minimize the offset between different observations of the same object at different time.
The resulting list of point source offsets is then merged with the planet offsets. Again a spline based correction is built fitting all of this data, and allowing rupture of continuity at the time of the SCS switchover and other major onboard event (typically between each surveys).
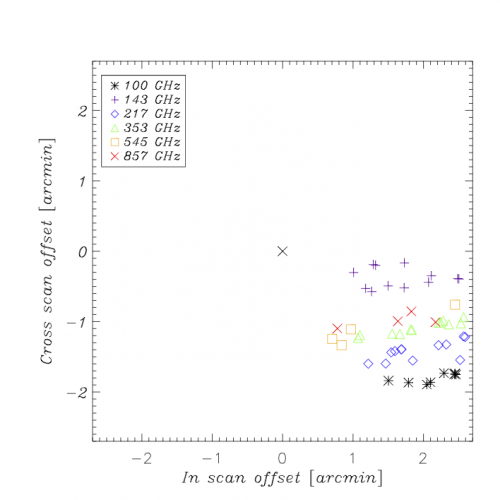
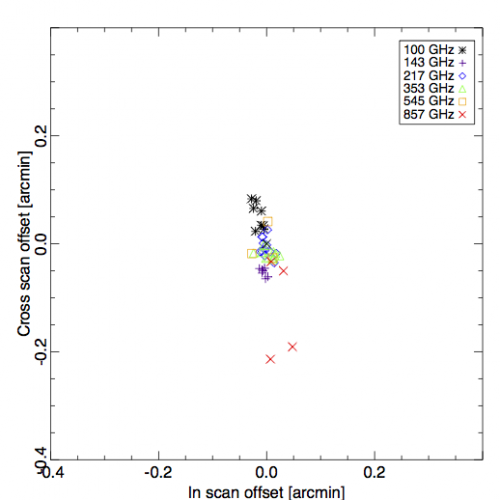
Once we assume the full Planck pointing model and re-measure the position of Mars for this observation, we see sub-arcsecond deviations (as expected); this gives an indication of the purely numerical limitations of the method. Further planet observations show the small remaining uncorrected drift present in the pointing model (note that cross-scan positions are measured with considerably less data than in-scan positions due to the scan strategy):
Redoing the single-survey map- and catalog-based computation with the corrected pointing shows that Planck has achieved the arcsecond-scale rms uncertainty of pointing:
A model for Planck LFI Pointing[edit]
The profiles and locations of the beams are determined from the four observations of Jupiter listed in Table 1. Details are given in Planck-2013-IV[4].
| Jupiter transit | Date | OD |
| Scan 1(J1) | 21/10/09 - 05/11/09 | 161-176 |
| Scan 2(J2) | 27/06/10 - 12/07/10 | 410-425 |
| Scan 3(J3) | 03/12/10 - 18/12/10 | 569-584 |
| Scan 4(J4) | 30/07/11 - 08/08/11 | 808-817 |
The origin of the focal plane is the optical line of sight defined in Planck-PreLaunch-XII[5]. In the LFI RIMO, the beam centres are given by four numbers, $\theta_{\mathrm uv}$, $\phi_{\mathrm uv}$, $\psi_{\mathrm uv}$, and $\psi_{\mathrm pol}$. Only $\theta_{\mathrm uv}$ and $\phi_{\mathrm uv}$, which are the beam pointing in spherical coordinates referred to the line of sight, can be determined with Jupiter observations. The polarization orientation of the beams, defined by $\psi_{\mathrm uv} + \psi_{\mathrm pol}$, is not estimated from flight data but is derived from main beam simulations based on ground measurements.
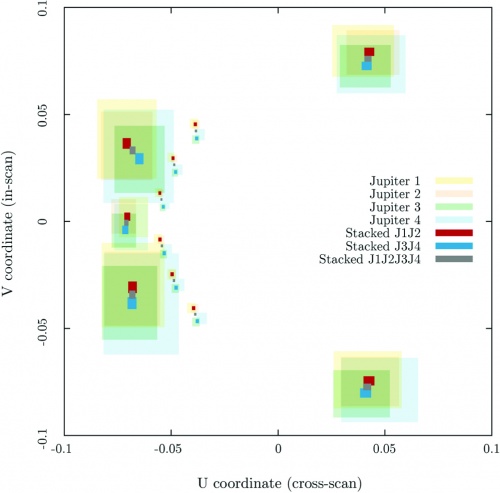
For each beam, the pointing is determined by the location of the maximum of an elliptical Gaussian fit to that beam. This was done for each beam in each single scan. Results are reported, with errors, in Planck-2013-IV[4]. In addition, the beams are stacked in pairs (J1J2 and J3J4) and all together (J1J2J3J4) in order to improve the signal-to-noise ratio of the measurements. Before the stacking, each beam is artificially repointed along the direction given by the arithmetic average of the centre of each beam to be stacked. Then a fit is performed again on the stacked beams and the resulting parameters recorded. For single scans it has been found that there is an agreement within 2 arcsec in the pointing direction between J1 and J2. The same agreement occurs between J3 and J4. In contrast, a 15 arcsec systematic deviation of the beam centre was detected when comparing J1J2 to J3J4. Figure below shows the reconstructed beam positions and errors in the line-of-sight frame magnified by a factor of 100. The shift is evident for the 70 GHz beams, as well as in all the J1J2 and J3J4 stacked beam centres. The change in the location has been found mainly in the scan direction (i.e., $v$-coordinate). To account for this pointing shift, we apply two pointing solutions for LFI. The first focal plane calibration is valid from OD91 to OD540 and is based on the J1J2 beam pointing determination. The second calibration is valid from OD541 to OD563 and is based on the J3J4 beam pointing calibration.
References[edit]
- ↑ Planck 2013 results: HFI time response and beams, Planck Collaboration 2013 VII, A&A, in press, (2014).
- ↑ Planck 2013 results: High Frequency Instrument Data Processing, Planck Collaboration 2013 VI, A&A, in press, (2014).
- ↑ The Imperial IRAS-FSC Redshift Catalogue, L. Wang, M. Rowan-Robinson, MNRAS, 398, 109--118, (2009).
- ↑ 4.04.1 Planck 2013 results: LFI Beams, Planck Collaboration 2013 IV, A&A, in press, (2014).
- ↑ Planck pre-launch status: The optical system, J. A. Tauber, H. U. Nørgaard-Nielsen, P. A. R. Ade, J. Amiri Parian, T. Banos, M. Bersanelli, C. Burigana, A. Chamballu, D. de Chambure, P. R. Christensen, O. Corre, A. Cozzani, B. Crill, G. Crone, O. D'Arcangelo, R. Daddato, D. Doyle, D. Dubruel, G. Forma, R. Hills, K. Huffenberger, A. H. Jaffe, N. Jessen, P. Kletzkine, J. M. Lamarre, J. P. Leahy, Y. Longval, P. de Maagt, B. Maffei, N. Mandolesi, J. Martí-Canales, A. Martín-Polegre, P. Martin, L. Mendes, J. A. Murphy, P. Nielsen, F. Noviello, M. Paquay, T. Peacocke, N. Ponthieu, K. Pontoppidan, I. Ristorcelli, J.-B. Riti, L. Rolo, C. Rosset, M. Sandri, G. Savini, R. Sudiwala, M. Tristram, L. Valenziano, M. van der Vorst, K. van't Klooster, F. Villa, V. Yurchenko, A&A, 520, A2+, (2010).
Attitude History File
(Planck) High Frequency Instrument
(Planck) Low Frequency Instrument
LFI Radiometer Electronics Box Assembly
Attitude Control & Measurement Subsystem (AOCS)
Interface Control Document
Star TRacker
Line Of Sight
Service Module
Operation Day definition is geometric visibility driven as it runs from the start of a DTCP (satellite Acquisition Of Signal) to the start of the next DTCP. Given the different ground stations and spacecraft will takes which station for how long, the OD duration varies but it is basically once a day.
sudden change of the baseline level inside a ring
Sorption Cooler Subsystem (Planck)
reduced IMO
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.