Difference between revisions of "HFI Detector Spectral Response"
| Line 68: | Line 68: | ||
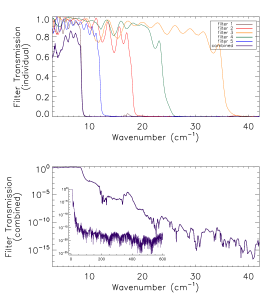
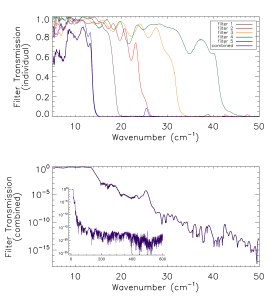
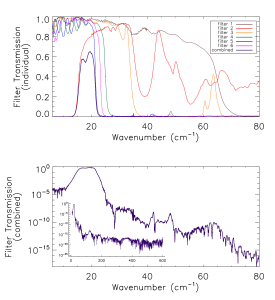
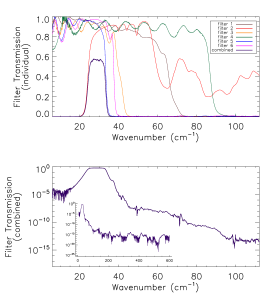
Prior to the IAS measurements with the integrated HFI detectors and filter stacks, FTS measurements of the individual filters comprising the filter stacks for each band were conducted at Cardiff. As will be discussed in §[sec:OOB], the independent measure of the filter stack transmission is used for a portion of the HFI detector spectral transmission for regions of the spectrum where it is deemed to be of better quality then the IAS FTS measurements (i.e. for frequencies outside of the band edge filter cut-off(s)). The filter stacks for each of the frequency bands are comprised of 5 filters. There is an additional low frequency cut-on filter for the 545 and 857 GHz bands as the waveguide cut-on is too low. Figures [fig:Filt100] – [fig:Filt857] show the individual filter transmission measurements as well as the combined filter stack product. | Prior to the IAS measurements with the integrated HFI detectors and filter stacks, FTS measurements of the individual filters comprising the filter stacks for each band were conducted at Cardiff. As will be discussed in §[sec:OOB], the independent measure of the filter stack transmission is used for a portion of the HFI detector spectral transmission for regions of the spectrum where it is deemed to be of better quality then the IAS FTS measurements (i.e. for frequencies outside of the band edge filter cut-off(s)). The filter stacks for each of the frequency bands are comprised of 5 filters. There is an additional low frequency cut-on filter for the 545 and 857 GHz bands as the waveguide cut-on is too low. Figures [fig:Filt100] – [fig:Filt857] show the individual filter transmission measurements as well as the combined filter stack product. | ||
| − | <gallery caption="Combined (bottom) and individual (top) filter transmission measurements for the 5 filters within the HFI band filter stacks (6 for 545 and 857 GHz)." widths=" | + | <gallery caption="Combined (bottom) and individual (top) filter transmission measurements for the 5 filters within the HFI band filter stacks (6 for 545 and 857 GHz)." widths="300px" heights="300px" perrow="3"> |
File:HFI_FilterPlots_100GHz.png|100GHz | File:HFI_FilterPlots_100GHz.png|100GHz | ||
File:HFI_FilterPlots_143GHz.png|143GHz | File:HFI_FilterPlots_143GHz.png|143GHz | ||
Revision as of 11:03, 4 October 2012
Contents
HFI Detector Spectral Response[edit]
Abstract[edit]
This section is comprised of excerpts from the HFI - Spectral Calibration report of the IAS measurements, v3.00, an internal report describing detailed pre-flight ground based measurements of the HFI focal plane. The experimental setup, data collection, and related data processing are described. The official version of the HFI detector spectral transmission profiles is available within the HFI instrument model and the RIMO files in the Planck Legacy archive [ref.] . This data is comprised of broadband Fourier transform spectrometer (FTS) measurements conducted with the HFI focal plane assembly as described above, and includes a waveguide model for the low frequency spectral region, and component-level filter spectra for the remaining out of band spectral regions. Specific attention is given to in-band and near-band spectral regions surrounding CO rotational transitions in order to support the CO extraction component separation effort [ref.] . The spectral transmission profiles are evaluated with parameters such as cut-on, cut-off, centre frequency, effective frequency (including spectral index), and band-width are provided in the analysis. Further evaluation yields band-average spectra ( [ref.] ) and unit conversion / colour correction coefficients ( [ref.] ) and software routines ( [ref.] ).
Objectives[edit]
The main goal of the spectral transmission tests of the HFI instrument is to measure the spectral response of all HFI detectors to a known source of EM radiation individually. This was determined by measuring the interferometric output of all detection channels for radiation propagated through a continuously scanned polarising fourier transform spectrometer (FTS). The required accuracy to which the spectral transmission is to be recovered is 1 (see §Req.).
It is important to note that the absolute spectral calibration cannot be achieved solely from the analysis of the FTS data because of uncertainties in the coupling efficiency of the FTS source through the FTS, input optics, and integrating sphere. The relative FTS measurements must be combined with the optical efficiency tests which used internal black-body sources (EFF Test – see §EFF).
Description of setup[edit]
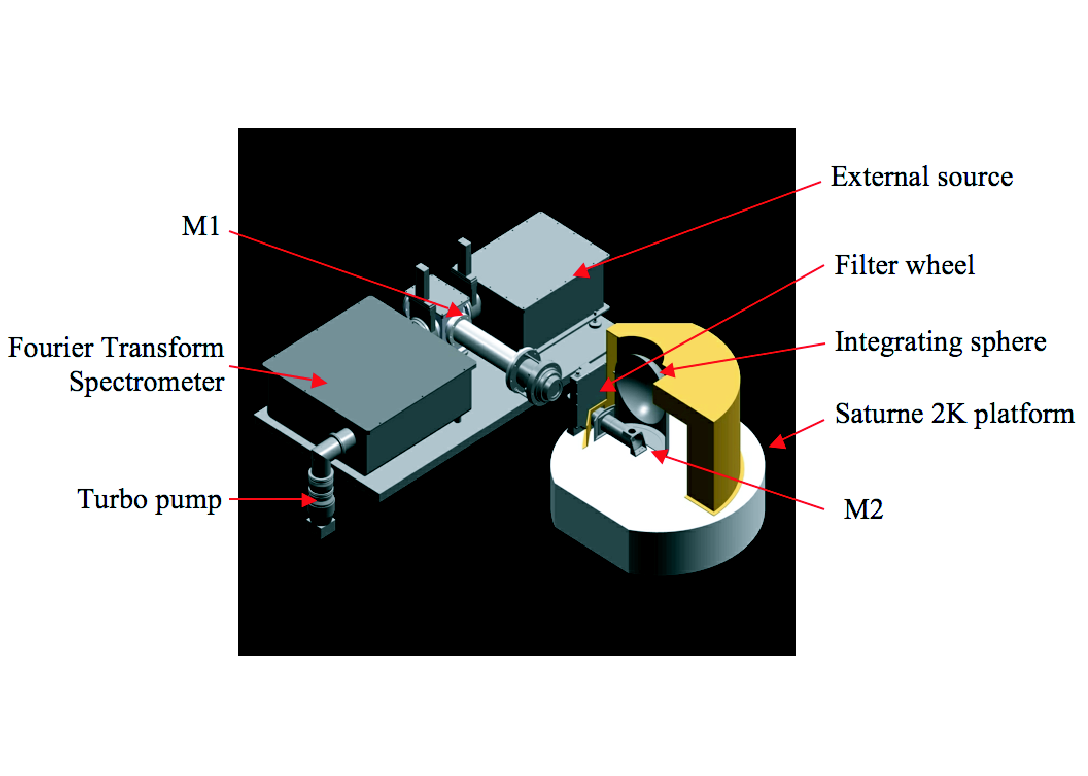
A brief description of the optical setup used for the spectral characterisation of the HFI instrument performed at the FPU level in the Saturne calibration facility at IAS is provided here. Further details are available from the pre-launch calibration papers . The spectrometer configuration is based on a polarizing Fourier transform interferometer, feeding an integrating sphere inside the Saturne tank (Figs. [fig:Optical-layout-of] & and [fig:Top-view-of]). The output of the integrating sphere is conjugated by a mirror with the focal plane of the HFI. Therefore data are acquired simultaneously on all pixels while the moveable mirror in the external FTS is scanned.
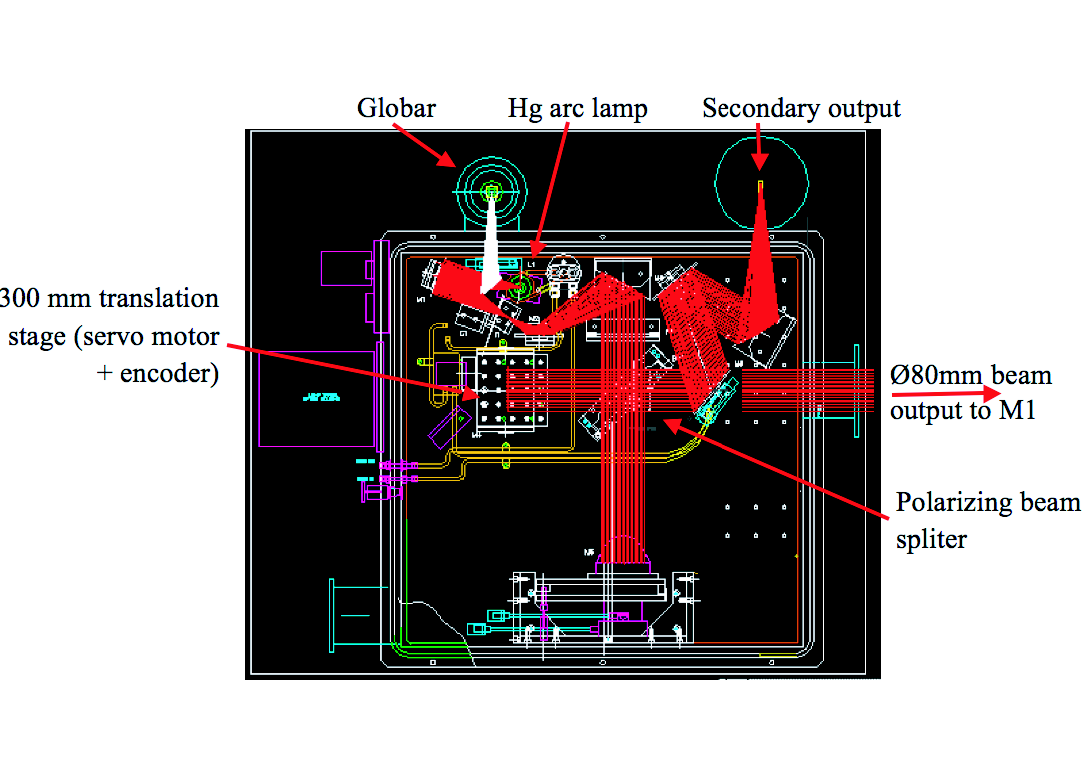
An external light source system (ELS, see Fig.[fig:FTS/ELS-assembly-with]) is provided in addition to the FTS for time constant measurements. Selection between the FTS and the ELS is done by the M1 flip mirror.
The polarising FTS was provided by Sciencetech Inc. (Canada) under contract with IAS and ESA (Fig.[fig:Internal-optical-layout]). The source can be selected from either a Hg vapour arc lamp or a globar. The 300 mm translation stage allows symmetric interferograms with a maximum theoretical (unapodized) Instrument Line Shape (ILS) Full-Width-at-Half-Maximum (FWHM) resolution of . Filtering of short wavelength is done on the optical path entering the Saturne cryostat as follows:
- Saturne vacuum window is polyethylene (6mm thick)
- thermal fiter at 300K
- thermal filter at 77K
- filter at 77K
- thermal filter at 20K
- filter wheel at 2K (Fig. [fig:2K-filter-wheel]) with selection of: open, closed, or filter
The optical flux from the FTS enters the integrating sphere through an 8mm diameter hole at its bottom (Fig. [fig:FTS-input-aperture]), which is the conjugate of the M1 mirror by M2.
During scanning, encoder pulses from the translation stage are time stamped with a clock synchronized with the HFI signal acquisition clock (itself provided by the spacecraft simulator used during the calibration). In a similar way, a mechanical ZPD (Zero Path Difference) signal is stamped and stored in the database. After verification, the scanning speed was found to be sufficiently stable to be assumed as constant along the section of the interferogram needed for spectral processing. Therefore the data processing described below does not use the reference signal but relies instead on the data acquisition time line to derive the optical path difference.
To provide a reference monitor for the interferometric flux, a dedicated bolometer is used within the integrating sphere. The flux recorded by this detector is directly related to the flux received by the HFI detectors on the focal plane which is coupled directly to the sphere output hole via mirror M1. The reference bolometer was provided by the team of N. Coron at IAS and has a predetermined absolute calibration between the flux measured and its output signal. It is fed by a modified Winston horn from Infrared Lab. Inc. (USA) and operated at 300 mK using a fridge (Torre-Chanin). The reference spectra acquired during the calibration run with this bolometer are used to identify standing wave features in the FTS source and path (lamp, windows,...) and to check the shape of the source spectrum. The diffraction losses at low frequencies due to the horn exit aperture diameter (2.6 mm ) is a limitation taken into account in the data processing of the low frequency channels of HFI.
Data Collection[edit]
To allow for data sets that have the same instrumental effects the bulk of the sequences have been performed with the same parameters. Also, separate single tests have been performed in different configurations to understand instrument systematics. The following is a list of the sequences adopted for the final spectral calibration data.
- Max OPD: The Maximum Optical Path Difference adopted during FTS testing is 30 cm. This relates to a nominal maximum resolution for the spectra of . This maximum resolution may then be deteriorated by the actual sample of data selected and by the apodization of the data (see §[sec:apod]).
- Speed: The Speed of the scanning FTS is set to for all of the data. The sampling of the data given by the acquisition frequency allows knowledge of the spectrum up to . This is well above the optical filter cut-off frequency, so aliasing is not a concern. The independent filter measurements used in the spectral transmission outside of the optical pass-band (see §[sec:filter]) have a Nyquist frequency of cm.
- Source: two sources were used in separate measurements. The mercury arc lamp as the main source for the final data and also a GLOBAR source to study any systematic effect present in the different measurements. (Although ratio with reference bolometer should remove such artifacts.) The spectra used to generate the Spectral Transmission data products in the IMO all originated from the mercury arc lamp as the optical source.
- Spectral range: The spectral range of the radiation entering the Saturne cryostat is given by a fixed LPE filter and a rotating filter wheel with the following positions (1- Open (no added filtering), 2- Dark (no radiation allowed), 3- LPE , 4- LPE ). The last two positions have been adopted for the final data of the three lower spectral channels (100, 143, 217 GHz) and the higher three spectral channels (353, 545, 857 GHz), respectively.
Additional Experiments[edit]
There were two significant additional tests that are used in the derivation of the HFI detector spectral transmission profiles beyond the scope of the IAS HFI FTS measurements. Additional filter measurements were recorded in the AIG test facility at Cardiff during filter stack production. These measurements are used to extend the IAS FTS spectral meaurements beyond the HFI spectral passband. The EFF tests are used to obtain optical efficiency parameters for each detector. These parameters, when combined with the respective normalized spectral transmission profiles, provide an estimate of the absolute spectral transmission. The EFF tests are discussed briefly in §EFF, with greater detail provided by A. Catalano . The filter measurements are described in §filter below.
Filter Measurements[edit]
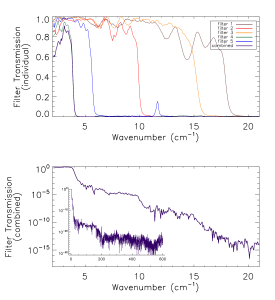
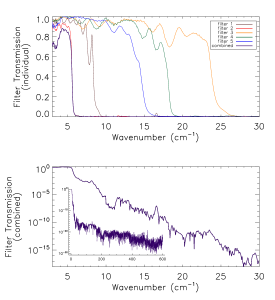
Prior to the IAS measurements with the integrated HFI detectors and filter stacks, FTS measurements of the individual filters comprising the filter stacks for each band were conducted at Cardiff. As will be discussed in §[sec:OOB], the independent measure of the filter stack transmission is used for a portion of the HFI detector spectral transmission for regions of the spectrum where it is deemed to be of better quality then the IAS FTS measurements (i.e. for frequencies outside of the band edge filter cut-off(s)). The filter stacks for each of the frequency bands are comprised of 5 filters. There is an additional low frequency cut-on filter for the 545 and 857 GHz bands as the waveguide cut-on is too low. Figures [fig:Filt100] – [fig:Filt857] show the individual filter transmission measurements as well as the combined filter stack product.
- Combined (bottom) and individual (top) filter transmission measurements for the 5 filters within the HFI band filter stacks (6 for 545 and 857 GHz).
The uncertainty on the combined filter transmission measurement is determined as follows. Let represent the individual filter transmission. The standard deviation of all values of below a threshold of is used as an approximate uncertainty for each individual filter measurement, i.e. . The individual uncertainty estimates are combined to provide an estimate of the combined filter transmission spectral uncertainty through standard error propagation. For the combined filter transmission represented as , the associated uncertainty estimate is given as
Raw Data[edit]
Table [tab:RawData] contains the details for the sets of data adopted for data analysis in the generation of the HFI detector spectral transmission profiles. The first two columns report the date and time of the starting point of the data set. The third column indicates the approximate scan length (in minutes). The fourth column is the maximum number of valid interferograms that are present in the data file. The column labeled RFP (Rotating Filter Wheel Position) indicates the filtering condition under which the data was taken: 1-Totally open (no filtering other than the ever present LPE; 2-Closed (no radiation is allowed to pass into the cryostat from the FTS); 3- LPE filter (for the low frequency channels); 4- LPE filter (for the high frequency channels). The column immediately following indicates, within a milliKelvin, the average reading of the bolometer plate thermometers during the scan time. The data sets with the RFP set to were used for the lower frequency channels, i.e. the 100, 143, and 217 GHz bands. The data corresponding to an RFP of were used for the higher frequency channels, i.e. the 353, 545, and 857 GHz bands. Table [tab:BrefData] indicates the data sets used to obtain the reference bolometer spectra. In most instances the data were acquired synchronously, however, there were cases when the HFI data was of good quality and the reference bolometer data was not, and vice-versa. The recorded data corresponding to the entries in Tables [tab:RawData] & [tab:BrefData] were used in the determination of the HFI spectral transmission profiles. There is also additional data that was recorded as part of the test campaign but not used in this specific work that is not listed here.
[bht]
|l|l|l|l|l|l|l|
Date (DD/MM/YY) & Time & size (min) & #Ifgm. & RFP & Source & <T(mK)> 25/06/06 & 07:52 & 25 & 4 & 4 & Hg & 140 25/06/06 & 08:33 & 25 & 4 & 4 & Hg & 140 25/06/06 & 09:02 & 65 & 12 & 4 & Hg & 140 25/06/06 & 10:05 & 65 & 12 & 4 & Hg & 140 25/06/06 & 11:15 & 65 & 12 & 4 & Hg & 140 26/06/06 & 09:44 & 25 & 4 & 4 & Hg & 140 27/06/06 & 17:48 & 148 & 28 & 3 & Hg & <130 27/06/06 & 20:20 & 335 & 50 & 3 & Hg & <120 28/06/06 & 21:39 & 163 & 28 & 3 & Hg & 95 05/07/06 & 06:23 & 82 & 16 & 4 & Hg & 100
[thb]
|l|l|l|l|l|l|
Date (DD/MM/YY) & Time & size (min) & #Ifgm. & RFP & Source 22/06/06 & 17:50 & 50 & 9 & 3 & Hg 22/06/06 & 18:40 & 50 & 9 & 3 & Hg 22/06/06 & 19:30 & 50 & 9 & 3 & Hg 22/06/06 & 20:20 & 50 & 9 & 3 & Hg 22/06/06 & 21:10 & 50 & 9 & 3 & Hg 22/06/06 & 22:50 & 50 & 9 & 3 & Hg 22/06/06 & 23:40 & 50 & 9 & 3 & Hg 25/06/06 & 07:52 & 25 & 4 & 4 & Hg 25/06/06 & 10:05 & 65 & 12 & 4 & Hg 25/06/06 & 11:15 & 65 & 12 & 4 & Hg 26/06/06 & 09:44 & 25 & 4 & 4 & Hg 26/06/06 & 17:04 & 38 & 7 & 3 & Hg 26/06/06 & 22:23 & 41 & 8 & 3 & Hg 27/06/06 & 00:04 & 86 & 16 & 3 & Hg 27/06/06 & 17:48 & 148 & 28 & 3 & Hg 27/06/06 & 20:20 & 335 & 50 & 3 & Hg 28/06/06 & 21:39 & 163 & 28 & 3 & Hg 05/07/06 & 06:23 & 82 & 16 & 4 & Hg
Data Processing[edit]
<1-- [sec:DP] -->
Having identified the data sections that are of interest, here follows the data processing sequence used to obtain the resulting spectra. The processing steps taken are as follows:
- Selection and extraction of time sampled data sets
- Conversion of time sampled data to arrays of OPD sampled interferogram data sets
- Fourier transformation and averaging of interferogram data sets
- Discrimination of poor quality spectra by standard deviation comparison (see §[sec:FTavg])
- Division of detector spectra by reference bolometer spectra to obtain normalized spectral transmission profiles
- Combination of relative transmission spectra with filter measurements and waveguide models
- Determination of optical efficiency through evaluation of normalized spectral transmission in the context of the EFF experiments
- Addition of over-sampled data into spectrum for the CO transition regions (see §[sec:CO])
- Identification of common frequency sampling per channel and interpolation of spectra onto the common sampling
Selection and extraction of data sets[edit]
The selected arrays of data are imported into a KST client from the QLA server
plck-op-3.ias.u-psud.fr
and subsequently exported as text files. Separate files are generated for the various bolometer signals and sample times for each detector. The exported text files were transferred from the remote IAS machines to the dedicated Planck computer at Cardiff,
planck01.astro.cf.ac.uk,
for further processing and analysis. A sample bolometer signal timeline is shown in Fig. [fig:BolSig].
The bolometer signal is stored within the initial database in several formats: raw ADU, signal voltage, resistance, current, temperature, total power, electrical power, and radiant power, all of which may be exported to a KST session as a function of sample time. Although all of the above formats originated from the recorded detector ADU signal and instrument model parameters, it was not possible to trace these refined database vectors to the specific bolometer parameters used in their conversion. Also exported from a KST session were the set balance voltages and bias currents for each detector so that a bolometer model using the current IMO parameters (IMO ver. 2_50) could be applied to the raw data as well. The motivation for the application of a bolometer model to the data was to reduce the in-band effects of detector nonlinearities as evidence of detector operation in a non-linear regime was identified within the raw data.
For the interferograms within each of the data sets in the above tables (Tab. [tab:RawData] & [tab:BrefData]), a course estimate of the temporal location of each position of Zero Optical-Path Difference (ZPD) was determined using the characteristic local maxima associated with a broad-band fringe for detectors with good S/N. This course ZPD location was then used as a starting point to identify a unique ZPD location within each interferogram through the fitting of a low order polynomial to the ZPD fringe.
The interferogram boundaries are determined as the mid-points between subsequent interferograms, less a small number of buffer points (10) to ensure that the extracted interferograms include regions associated with the FTS stage travel having constant velocity while excluding the acceleration regions.
Visual verification of the extracted interferograms is performed to ensure that each ZPD was identified correctly and to remove any low-quality interferograms. The overlap of the extracted interferograms is also verified visually, with any anomolies either corrected (through a revised ZPD location) or removed. These interferograms are then saved to separate files, to be combined as a large dataset further on in the processing.
Once interferograms have been extracted from each data set, they are combined into a single array for each detector. The Maximum Optical Path Difference (MPD) is determined for each interferogram, and the minimum for each detector within a combined data set is used to generate an evenly sampled Optical Path Difference (OPD) grid onto which each interferogram in the combined data is then interpolated. This ensures that each individual interferogram is sampled at ZPD and that each spectrum has identical frequency sampling and can thus be averaged together. An example of a combined interferogram data set is illustrated in Figure [fig:CombinedIFGMex] where the central portions of the recorded interferograms are shown. A similar plot for each HFI detector is included in the Appendices (see §[sec:allIFGMs]). The MPD value for each detector, and corresponding spectral resolution, is shown in Fig. [fig:MPD].
/figures/LSfigs/
Fourier Transformation and Averaging of Interferogram Data Sets[edit]
In preparation for Fourier transformation, a low-order polynomial baseline removal is performed on the individual interferograms. Consequently, no information can be recovered from the spectrum below , but this is of no concern as this region of the spectrum is replaced by a waveguide fit in the final data product (see §[sec:WG]). An average interferogram is determined and used to identify glitches for removal from the interferogram data. If possible, the exponentially decaying tail of a glitch is identified, fit, removed, and replaced by the average of the remainder of the data set (which does not contain a glitch). If this is not possible then the entire interferogram is removed from the data set.
Although an average interferogram is determined, it is not directly used in obtaining the average spectrum. Once the data set has been deglitched, individual interferograms may be apodized (see §[sec:apod]), and then undergo Fourier transformation and phase correction . To allow phase correction to take place at the individual interferogram level, data averaging is then performed in the spectral domain. The uncertainty for every spectral data point is determined statistically through the standard deviation at a given frequency. A check for poor quality spectra is performed by comparing the overall standard deviation including and excluding any given spectrum. An example of the individual spectra and uncertainty for bc00 is shown in Fig. [fig:CombinedSpecEx]; similar plots for all of the detectors are shown in §[sec:allSpecs].
Table [tab:Igstats] contains information on the individual detector data sets for each of the HFI detectors. Columns three and four contain the number of interferograms and spectra, respectively, used in the generation of subsequent data. These numbers may disagree due to the discrimination of poor quality data discussed above. There will never be more spectra than interferograms for a given data set. The fifth column indicates the minimum MPD for the detector data set. The FTS Instrument Line Shape (ILS) Full-Width-at-Half-Maximum (FWHM) for the data set is provided in the sixth column. An estimate of the S/N is obtained using the average spectrum and its statistical uncertainty, averaged across the in-band region of the spectrum.
The averaged spectra are then normalized and divided by a (normalized) reference bolometer spectrum (see §[sec:setup] & §[sec:Bref]). This is done to remove spectral features from the data beyond those due to the HFI optics and detectors. The terminology ‘pre-ratio’ is used to refer to the spectra before division by the reference bolometer spectra.
|c|c|c|c|c|c|c|
| Band |
| (GHz) |
& bc & # Ifgm. & # Spec. & MPD (cm) & ILS (cm) & avg. S/N
| Band |
| (GHz) |
& bc & # Ifgm. & # Spec. & MPD (cm) & ILS (cm) & avg. S/N
100 & 00 & 96 & 93 & 29.648639 & 0.020355066 & 104.70555
100 & 01 & 96 & 95 & 29.648639 & 0.020355066 & 203.34226
100 & 20 & 96 & 96 & 29.649801 & 0.020354268 & 271.38262
100 & 21 & 95 & 94 & 29.650962 & 0.020353471 & 264.65385
100 & 40 & 96 & 94 & 29.652124 & 0.020352674 & 432.40921
100 & 41 & 96 & 96 & 29.652124 & 0.020352674 & 962.98064
100 & 80 & 95 & 95 & 29.650962 & 0.020353471 & 262.71036
100 & 81 & 96 & 96 & 29.650962 & 0.020353471 & 227.35782
143 & 02 & 96 & 95 & 29.652124 & 0.020352674 & 434.93136
143 & 03 & 96 & 96 & 29.652124 & 0.020352674 & 458.86741
143 & 10 & 95 & 95 & 29.652124 & 0.020352674 & 565.21311
143 & 30 & 92 & 92 & 29.653286 & 0.020351876 & 424.53824
143 & 31 & 92 & 92 & 29.652124 & 0.020352674 & 447.50343
143 & 42 & 92 & 92 & 29.652124 & 0.020352674 & 536.23423
143 & 50 & 96 & 96 & 29.652124 & 0.020352674 & 441.68983
143 & 51 & 96 & 96 & 29.652124 & 0.020352674 & 476.22684
143 & 60 & 96 & 96 & 29.652124 & 0.020352674 & 517.43269
143 & 70 & 95 & 94 & 29.652124 & 0.020352674 & 326.06542
143 & 82 & 96 & 96 & 29.652124 & 0.020352674 & 454.23293
143 & 83 & 96 & 96 & 29.652124 & 0.020352674 & 439.50612
217 & 04 & 96 & 96 & 29.652124 & 0.020352674 & 625.92713
217 & 11 & 96 & 96 & 29.652124 & 0.020352674 & 580.32904
217 & 12 & 67 & 67 & 29.663741 & 0.020344703 & 549.24264
217 & 22 & 96 & 96 & 29.652124 & 0.020352674 & 550.65242
217 & 43 & 95 & 95 & 29.652124 & 0.020352674 & 616.57750
217 & 44 & 96 & 96 & 29.652124 & 0.020352674 & 543.78288
217 & 52 & 95 & 94 & 29.652124 & 0.020352674 & 684.91039
217 & 61 & 92 & 92 & 29.652124 & 0.020352674 & 594.70296
217 & 62 & 95 & 95 & 29.652124 & 0.020352674 & 579.69385
217 & 71 & 96 & 96 & 29.652124 & 0.020352674 & 631.30065
217 & 72 & 96 & 96 & 29.652124 & 0.020352674 & 687.10844
217 & 84 & 92 & 92 & 29.652124 & 0.020352674 & 636.36790
353 & 05 & 55 & 55 & 29.651916 & 0.020352816 & 354.15815
353 & 13 & 57 & 57 & 29.651916 & 0.020352816 & 319.09858
353 & 23 & 55 & 55 & 29.651916 & 0.020352816 & 218.05772
353 & 24 & 64 & 64 & 29.651916 & 0.020352816 & 236.44464
353 & 32 & 56 & 56 & 29.651916 & 0.020352816 & 238.40018
353 & 33 & 55 & 55 & 29.651916 & 0.020352816 & 219.60443
353 & 45 & 64 & 64 & 29.653078 & 0.020352019 & 246.97889
353 & 53 & 57 & 57 & 29.651916 & 0.020352816 & 225.27621
353 & 54 & 57 & 57 & 29.651916 & 0.020352816 & 228.47058
353 & 63 & 57 & 56 & 29.651916 & 0.020352816 & 140.16991
353 & 64 & 55 & 55 & 29.651916 & 0.020352816 & 158.85037
353 & 85 & 57 & 57 & 29.653078 & 0.020352019 & 246.18460
545 & 14 & 63 & 63 & 29.654240 & 0.020351221 & 448.67624
545 & 34 & 64 & 64 & 29.654240 & 0.020351221 & 481.87111
545 & 55 & 57 & 57 & 29.654240 & 0.020351221 & 328.07835
545 & 73 & 57 & 57 & 29.654240 & 0.020351221 & 447.49901
857 & 25 & 64 & 64 & 29.653078 & 0.020352019 & 501.25106
857 & 35 & 64 & 64 & 29.654240 & 0.020351221 & 567.55125
857 & 65 & 42 & 42 & 29.653078 & 0.020352019 & 482.41906
857 & 74 & 64 & 64 & 29.654240 & 0.020351221 & 491.89133
Apodization[edit]
Apodization of FTS interferograms results in reduced sidelobes of the FTS spectral ILS, at the cost of broadening the central feature of the ILS itself. Another perspective is that the interferogram is prefferentially weighted at certain OPD regions (i.e. ZPD) over others prior to Fourier transformation. This also, ideally, results in an improvement in the spectral S/N for a broad-spectrum source, again at the cost of reduced spectral resolution. Figure [fig:apodKernel] illustrates a variety of interferogram apodization kernels that have been used in this work . The modified Norton-Beer 1.5 apodization function has been selected to be used for the final spectral transmission profile data set as it represents a good compromise between the desired ILS sidelobe reduction and improved S/N with marginal reduction in spectral resolution. Figure [fig:ApodCompare] illustrates the difference between apodizations on the same sample data.
Reference Bolometer Spectra[edit]
The reference bolometer spectra are obtained in a fashion similar to that used for the HFI detectors. Wherever possible, the same data processing is applied to the reference bolometer data as was applied to the HFI detector data, including RFP setting, scan speed, scan length, source intensity, apodization, phase correction, etc. Table [tab:Brefstats] contains the reference bolometer data set properties corresponding those listed for the HFI detectors in Table [tab:Igstats]. Figures [fig:BrefL] - [fig:Bref857] illustrate the resultant spectra and S/N from the reference bolometer data sets. Figure [fig:SNall] compares the approximate S/N of the average spectrum for each detector against the reference bolometer average spectrum S/N over the same spectral region.
|c|c|c|c|c|c|c|
<tbody> </tbody>| Band |
| (GHz) |
& RFP & # Ifgm. & # Spec. & MPD (cm) & ILS (cm) & avg. S/N
100 & 3 & 164 & 164 & 29.644698 & 0.020357772 & 11.478057
143 & 3 & 164 & 164 & 29.644698 & 0.020357772 & 37.361317
217 & 3 & 164 & 164 & 29.644698 & 0.020357772 & 126.14280
353 & 4 & 24 & 24 & 29.652306 & 0.020352549 & 136.06159
545 & 4 & 24 & 24 & 29.652306 & 0.020352549 & 314.58093
857 & 4 & 24 & 24 & 29.652306 & 0.020352549 & 388.23050
Out-of-Band Spectral Transmission Content[edit]
The HFI detector spectral transmission profiles have been extended beyond the optical pass-band of the detectors. This is done by using a combination of a waveguide model and external filter measurements for the out-of-band regions of the detector spectral response. An uncertainty estimate for these additional spectral regions is also provided, however, it should be noted that the spectral uncertainty for the waveguide and filter spectra are determined indirectly (as described above/below).
There is a transition from IAS FTS data to filter data for every band edge which is defined by an optical filter. For the 100, 143, 217, and 353 GHz bands this is the high frequency cut-off band edge. For the 545 and 857 GHz bands a separate filter is used to define each of the high and low frequency band edges. For the spectral regions outside of the HFI detector optical bands, first the IAS FTS data is used to qualitatively verify that there are no spectral leaks or features, and then the external filter measurements are grafted into the ratioed spectra where they better represent the relative spectral transmission. The spectral transmission profiles switch from the ratioed IAS FTS data to the filtered data as follows:
- The normalized ratioed spectrum is scaled by the optical efficiency (see §[sec:EFF]) whereas the filter spectrum remains normalized. This results in a conservative over-estimation of the out-of-band transmission.
- A lower threshold frequency, , is defined for each band, below which the FTS data must be used.
- An upper threshold frequency, , is defined for each band, above which the filter data must be used. The is defined to be twice the band cut-on frequency. This is done to avoid introducing any detector nonlinearity residuals into the final spectral transmission data products.
- The region between the lower and upper threshold frequencies is defined as the transition region.
- The transition point is defined as the first data point in the transition region where the ratioed FTS spectrum is greater in amplitude than the filter spectrum.
- If no such transition point exists, the filter spectrum is temporarily scaled to be smaller until a transition point is identified, after which the filter spectrum is restored to its original amplitude. If the temporary filter data scaling becomes less than 0.01 then the upper threshold frequency is defined as the transition point.
- The filter spectrum is used for the transmission profile for all frequencies greater than and equal to the transition frequency.
- The above method resulted in a mild distortion to the spectrum within the transition region for the 143 and 857 GHz spectra. This was a result of nonlinearity features in the FTS spectra just before the transition region cut-off. In these cases, a comparison between the FTS data derivative and filter data derivative was used to determine the transition point, instead of using the spectral amplitudes.
Additionally, a similar technique is used, with decreasing frequency instead of increasing, for the 545 and 857 GHz bands with a filter-induced frequency cut-on. Figure [fig:OOBex] illustrates an example of both the FTS and filter spectra used in extending the transmission profiles beyond the HFI optical bands. Similar plots for every detector are shown in §[sec:stitch].
Waveguide Model[edit]
A waveguide model is used to provide the data for the lowest frequency portion of the HFI detector spectral transmission. For the 100, 143, 217, and 353 GHz bands the waveguide model is transitioned (with increasing frequency) to the FTS ratioed spectra directly. There is an intermediate transition to the filter data, and then the ratioed spectra for the 545 and 857 GHz bands. For each detector, the waveguide transmission, , is given by the following relation
where is the frequency in cm, is the waveguide radius in cm, is the waveguide length in cm, and is a waveguide specific constant; 1.841 for the TE/TM (HE) hybrid mode in this case . Table [tab:WG] lists the waveguide radii and lengths resultant from the waveguide model fit to the ratioed spectra. As all of the feedhorns for a given band are meant to be identical (i.e. within mechanical manufacturing tolerances) the uncertainty of the waveguide transmission is estimated statistically using all of the waveguide models for each band. I.e. for bands, the uncertainty at each spectral data point is determined by the standard deviation of transmission values at that frequency. As a result of each detector in a given band having a unique cut-on frequency, this method begins to over-estimate the uncertainty for frequencies approaching the cut-on; for regions very near the waveguide cut-on, the uncertainty is extrapolated from the ratioed spectrum as a more accurate representation.
|c|c|c|c|c|
Band (GHz) & bc & Det. & (mm) & (mm)
Band (GHz) & bc & Det. & (mm) & (mm)
100 & 00 & 1a & 1.039705 & 12.1000
100 & 01 & 1b & 1.038040 & 12.5813
100 & 20 & 2a & 1.038375 & 14.3000
100 & 21 & 2b & 1.041035 & 12.3750
100 & 40 & 3a & 1.042370 & 12.9250
100 & 41 & 3b & 1.042370 & 12.5125
100 & 80 & 4a & 1.033050 & 13.2000
100 & 81 & 4b & 1.033050 & 12.6500
143 & 02 & 1a & 0.740345 & 9.4500
143 & 03 & 1b & 0.737550 & 9.5625
143 & 10 & 5 & 0.736155 & 9.4500
143 & 30 & 2a & 0.740345 & 9.4500
143 & 31 & 2b & 0.739880 & 9.2250
143 & 42 & 6 & 0.741275 & 9.4500
143 & 50 & 3a & 0.741275 & 9.4500
143 & 51 & 3b & 0.741275 & 9.4500
143 & 60 & 7 & 0.729635 & 9.7875
143 & 70 & 8 & 0.739415 & 9.4500
143 & 82 & 4a & 0.739415 & 9.4500
143 & 83 & 4b & 0.738480 & 9.4500
217 & 04 & 1 & 0.4740750 & 7.8000
217 & 11 & 5a & 0.4814250 & 7.8000
217 & 12 & 5b & 0.4817310 & 8.0000
217 & 22 & 2 & 0.4749935 & 7.8000
217 & 43 & 6a & 0.4832625 & 8.0000
217 & 44 & 6b & 0.4832625 & 8.0000
217 & 52 & 3 & 0.4753000 & 8.0000
217 & 61 & 7a & 0.4820375 & 8.0000
217 & 62 & 7b & 0.4820375 & 8.0000
217 & 71 & 8a & 0.4838750 & 8.0000
217 & 72 & 8b & 0.4838750 & 8.1000
217 & 84 & 4 & 0.4740750 & 7.6000
353 & 05 & 1 & 0.2921850 & 6.47500
353 & 13 & 2 & 0.2914300 & 7.00000
353 & 23 & 3a & 0.2891650 & 7.70000
353 & 24 & 3b & 0.2893535 & 7.52500
353 & 32 & 4a & 0.2869000 & 7.35000
353 & 33 & 4b & 0.2870890 & 7.39375
353 & 45 & 7 & 0.2876550 & 6.12500
353 & 53 & 5a & 0.2936950 & 7.35000
353 & 54 & 5b & 0.2936950 & 7.61250
353 & 63 & 6a & 0.2929400 & 6.73750
353 & 64 & 6b & 0.2925625 & 6.62500
353 & 85 & 8 & 0.2889765 & 6.73750
545 & 14 & 1 & 0.3861000 & 3.600
545 & 34 & 2 & 0.3865875 & 3.525
545 & 55 & 3 & 0.3800065 & 3.525
545 & 73 & 4 & 0.3787875 & 3.525
857 & 25 & 1 & 0.2985 & 2.4
857 & 35 & 2 & 0.2985 & 2.4
857 & 65 & 3 & 0.2985 & 2.4
857 & 74 & 4 & 0.2985 & 2.4
Optical Efficiency[edit]
The EFF tests involved exposing the HFI detectors to a known blackbody source and observing the response. Sufficient details for the HFI detector spectral transmission profiles are provided here while full details of the EFF experiments and results are provided in a separate technical report . A blackbody source internal to the Saturne cryostat was set to a variety of temperatures (1 – 6 K) and the bolometer detector response was recorded. A bolometer model was applied to the recorded response in order to obtain the radiative optical power absorbed by the detector, in units of W, i.e. where represents the blackbody source temperature. Using the measured source temperature, the theoretical radiative optical power incident on the detector is also calculated using the Planck function. The ratio of the received power and the theoretical power provides the optical efficiency term. To remove any offsets in the measurement, a ratio of differences between unique temperature settings is used. The measured absorbed optical power difference is given by
where and represent two unique source temperature settings. The theoretical incident power is determined using the HFI detector spectral transmission profiles. Let represent the normalized detector transmission spectrum (i.e. it has been ratioed and had the waveguide model and filter data appropriately grafted). The spectral transmission is scaled for throughput and then re-normalized as follows
where is the division of by its maximum value, and is the speed of light. The normalized spectral transmission is then used with the Planck function at the temperature setting to determine the theoretical power, , as follows
where is the Planck constant, is the Boltzmann constant, the integration limits are given by and , and is the expected mode content of the frequency band. Table [tab:modes] lists the values used for each band . In this case the integration is performed over the range . The difference between the theoretical power loading is given by
which allows the optical efficiency term to be determined as follows
Thus, if were used in Equation [eq:EFFPth] in place of , the resultant optical efficiency would be unity, indicating that the transmission losses have already been taken into account.
The uncertainty estimate of the optical efficiency is statistically based on the results from the multiple temperature settings used in the EFF test sequences.
| Band (GHz) | 100 | 143 | 217 | 353 | 545 | 857 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 3.4 | 8.3 |
CO interpolation[edit]
The IAS FTS/Saturne data taken with the HFI detectors is limited to a spectral resolution of by the mechanical travel of the FTS translation stage. This corresponds to an unapodized FTS ILS FWHM of . The previous iteration of the spectral transmission (IMO ver. 2_28), in addition to a triangular apodization kernel, has a factor of 3 sub-sampled spectral resolution to improve the signal-to-noise ratio (S/N) of the output spectra. In light of the CO contribution to the 100 GHz spectra, the spectral transmission has been reprocessed at the original full spectral resolution with a different apodization function which provides better noise reduction and less spectral resolution degradation, as discussed above.
In order to provide an improved estimate of the spectral transmission near the CO features, an interpolation of the spectra by a factor of 10 has been performed. This over-sampling was accomplished by zero-padding the FTS interferograms prior to Fourier transformation , and subsequently incorporated into the Nyquist-sampled spectral data near the CO transitions (see Table [tab:CO]). Although the data are presented at higher resolution, the resolution of independent data points is not improved, i.e. the ILS line-width remains the same. A flag column has been added to the spectral transmission profile data files to indicate whether a given data point originates from the actual data, or is a result of the ILS-based interpolation. The region of the over-sampled, interpolated, data has been extended to also include other CO isotopes; the COJ1-0 – J9-8 transitions should be oversampled for CO, CO, CO, and CO. The original data points within the over-sampled region have been preserved (i.e. every tenth data point – the data point that is not an interpolated one – is flagged with a zero rather than a one), as is indicated by the data flag, so a flag filter on the data will restore the independent data points easily. Figure [fig:COflag] illustrates the regions where the over-sampling has been incorporated into the spectral transmission profiles. An example of the over-sampled spectra is shown in Figure [fig:COzoom100] for the 100 GHz detectors. Examples for the other detector bands are shown in §[sec:COappend]
|c|c|c|c|
<tbody> </tbody>| Band |
| (GHz) |
& CO transition () & (GHz) & over-sampled region (GHz)
100 & 1 – 0 & 115.2712018 & 109.67 – 115.39
217 & 2 – 1 & 230.5380000 & 219.34 – 230.77
353 & 3 – 2 & 345.7959899 & 329.00 – 346.15
545 & 4 – 3 & 461.0407682 & 438.64 – 461.51
545 & 5 – 4 & 576.2679305 & 548.28 – 576.85
857 & 6 – 5 & 691.4730763 & 657.89 – 692.17
857 & 7 – 6 & 806.6518060 & 767.48 – 807.46
857 & 8 – 7 & 921.7997000 & 877.04 – 922.73
857 & 9 – 8 &1036.9123930 & 986.57 – 1037.95
|c|c|c|c|c|
| Band |
| (GHz) |
& BC & Det. & CO transition () & Transmission
| Band |
| (GHz) |
& BC & Det. & CO transition () & Transmission
100 & 00 & 1a & 1 – 0 & 0.1495 0.0054
100 & 01 & 1b & 1 – 0 & 0.1812 0.0052
100 & 20 & 2a & 1 – 0 & 0.2577 0.0119
100 & 21 & 2b & 1 – 0 & 0.1944 0.0086
100 & 40 & 3a & 1 – 0 & 0.2798 0.0133
100 & 41 & 3b & 1 – 0 & 0.1660 0.0093
100 & 80 & 4a & 1 – 0 & 0.2538 0.0114
100 & 81 & 4b & 1 – 0 & 0.2173 0.0105
217 & 04 & 1 & 2 – 1 & 0.3781 0.0026
217 & 11 & 5a & 2 – 1 & 0.4530 0.0029
217 & 12 & 5b & 2 – 1 & 0.4174 0.0030
217 & 22 & 2 & 2 – 1 & 0.3773 0.0026
217 & 43 & 6a & 2 – 1 & 0.3149 0.0023
217 & 44 & 6b & 2 – 1 & 0.3609 0.0030
217 & 52 & 3 & 2 – 1 & 0.3924 0.0025
217 & 61 & 7a & 2 – 1 & 0.3428 0.0022
217 & 62 & 7b & 2 – 1 & 0.2770 0.0017
217 & 71 & 8a & 2 – 1 & 0.4623 0.0031
217 & 72 & 8b & 2 – 1 & 0.4340 0.0031
217 & 84 & 4 & 2 – 1 & 0.3506 0.0025
353 & 05 & 1 & 3 – 2 & 0.4487 0.0036
353 & 13 & 2 & 3 – 2 & 0.5461 0.0044
353 & 23 & 3a & 3 – 2 & 0.3443 0.0030
353 & 24 & 3b & 3 – 2 & 0.4706 0.0037
353 & 32 & 4a & 3 – 2 & 0.3099 0.0024
353 & 33 & 4b & 3 – 2 & 0.2801 0.0027
353 & 45 & 7 & 3 – 2 & 0.2923 0.0022
353 & 53 & 5a & 3 – 2 & 0.3150 0.0024
353 & 54 & 5b & 3 – 2 & 0.3181 0.0023
353 & 63 & 6a & 3 – 2 & 0.2059 0.0014
353 & 64 & 6b & 3 – 2 & 0.2113 0.0017
353 & 85 & 8 & 3 – 2 & 0.3509 0.0028
545 & 14 & 1 & 4 – 3 & 0.0747 0.0003
545 & 34 & 2 & 4 – 3 & 0.0731 0.0003
545 & 55 & 3 & 4 – 3 & 0.0521 0.0002
545 & 73 & 4 & 4 – 3 & 0.0473 0.0002
545 & 14 & 1 & 5 – 4 & 0.3306 0.0012
545 & 34 & 2 & 5 – 4 & 0.3183 0.0011
545 & 55 & 3 & 5 – 4 & 0.2428 0.0009
545 & 73 & 4 & 5 – 4 & 0.2597 0.0009
857 & 25 & 1 & 6 – 5 & 0.0280 0.0001
857 & 35 & 2 & 6 – 5 & 0.0241 0.0001
857 & 65 & 3 & 6 – 5 & 0.0292 0.0001
857 & 74 & 4 & 6 – 5 & 0.0159 0.0001
857 & 25 & 1 & 7 – 6 & 0.1636 0.0005
857 & 35 & 2 & 7 – 6 & 0.1427 0.0004
857 & 65 & 3 & 7 – 6 & 0.2176 0.0007
857 & 74 & 4 & 7 – 6 & 0.1168 0.0003
857 & 25 & 1 & 8 – 7 & 0.2554 0.0009
857 & 35 & 2 & 8 – 7 & 0.2218 0.0007
857 & 65 & 3 & 8 – 7 & 0.2744 0.0009
857 & 74 & 4 & 8 – 7 & 0.1119 0.0004
857 & 25 & 1 & 9 – 8 & 0.0053 0.0000
857 & 35 & 2 & 9 – 8 & 0.0060 0.0000
857 & 65 & 3 & 9 – 8 & 0.0085 0.0000
857 & 74 & 4 & 9 – 8 & 0.0001 0.0000
Conformity with requirements[edit]
The two defining requirements indicated in the HFI calibration plan are the acquisition of the spectral transmission of the single pixels with a prescribed accuracy and spectral resolution. The desired accuracy is 3% for the low frequency channels (CMB – 100, 143, and 217 GHz) and 1% for the high frequency channels (353, 545, 857 GHz). The spectral resolution requirement is for a resolution superior to 0.1 cm.
The spectral resolution requirement has been exceeded by more than a factor of five. It is also possible to degrade the spectral resolution to the 0.1 cm requirement to gain an improvement in the S/N.
No quantitative number is present on the document regarding the blocking of high frequency (near IR, visible, UV) radiation outside the range of the instrument. Checks in order to quantify the rejection have been performed at subsystem level and estimates of the out-of-band transmission profiles have been incorporated into the data products.
The requirement on the spectral transmission accuracy for the CMB channels is of . There is also a requirement that the high frequency channels effective frequencies be known to within ; knowledge of the transmission to 1% accuracy should allow this.
Considering statistical fluctuations in the determination of the spectra, these goals have been achieved. There are, however, caveats regarding the nature of error bars when dealing with frequency space. The nature of uncertainties in spectra determination is less obvious than when dealing with timestream data. Systematic effects produced from instrumental setup, but also by data reduction can in some cases exceed the actual statistical oscillation in the determination of the final spectra. This is the case for the high-frequency data for instance where the statistical fluctuation of the different determinations of the spectra in some case are better than 1 part in .
A second caveat regards the method of data analysis of the calibration test data, for which the ratio with the reference bolometer data (of which the relative error is a function of frequency) introduces an error that increase with wavelength. With the spectral resolution of the data provided being much higher that the stated 0.1 cm, the transmission accuracy requirement is not met for the 100 GHz detectors. It is possible to degrade the spectral resolution to the 0.1cm level to allow the accuracy to achieve the required level, but the higher spectral resolution data has been provided to better assist with the CO contamination removal from the 100 GHz signal.
(Planck) High Frequency Instrument
Focal Plane Unit
European Space Agency
Instrument Line Shape
Full-Width-at-Half-Maximum
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.
LFI Waveguide
Cosmic Microwave background