Difference between revisions of "Map-making"
(→Introduction) |
|||
| (158 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| − | {{DISPLAYTITLE: | + | {{DISPLAYTITLE:HFI Mapmaking and photometric calibration}} |
== Introduction == | == Introduction == | ||
| + | |||
| + | This section gives an overview of the mapmaking and the calibration procedures used to build the HFI maps. | ||
| + | * Procedures for the 2013 release is to be found in {{PlanckPapers|planck2013-p03}} and {{PlanckPapers|planck2013-p03b}} (see at the bottom of this page) | ||
| + | * Procedures for the 2015 release is to be found in {{PlanckPapers|planck2014-a09}} (see at the bottom of this page) | ||
| + | * In 2016, a new procedure called ''SRoll'' has been introduced to extract, from the sky, parameters for systematics important to the mapmapking. This is achieved through a generalized polarized destriper which uses the redundancy between detectors inside a frequency band. Systematic effects producing leakages from intensity to polarization contribute strongly to this determinations. This allowed for the first time the use of large scale polarized data and the extraction of the reionization parameter. The procedure and its results are described in {{PlanckPapers|planck2016-XLVI}}. | ||
| + | * For the 2018 legacy release, the same ''SRoll'' procedure has been used to produce the frequency intensity and polarization maps. {{PlanckPapers|planck2016-l03}} fully describes the procedures, the products and their characterization. | ||
| + | |||
| + | == ''SRoll'' global solution == | ||
| + | ===Inputs to ''SRoll''=== | ||
| + | |||
| + | For the 2018 release, the TOI processing remains unchanged from the previous 2015 release (see [[TOI_processing|TOI processing]]). As mentionned, a small cut of in the data selection (1000 pointing periods) has been done at the end of the cryogenic mission. | ||
| + | |||
| + | === ''SRoll'' scheme === | ||
| + | ''SRoll'' makes use of an extended destriper. Destriper methods have been used previously to remove baseline drifts from detector time streams, while making co-added maps of the data, by taking advantage of the redundancy in the scanning strategy. ''SRoll'' is a generalized polarized destriper which, in addition, compares all the observations of the same sky pixel by the same detector with different polarization angles, as well as by different detectors within the same frequency band. It thus fits differences between instrument parameters that minimize the difference between all polarized observations of the same sky pixel in the same frequency band. It solves consistently for: | ||
| + | * one offset for each pointing period, | ||
| + | * an empirical transfer function adding to the correction already done in the TOI processing (time constants less than 3 seconds), covering time constants up to 30 seconds, | ||
| + | * a CMB calibration mismatch between detectors, detected through the shift on the total kinetic dipole, between odd and even surveys, inducing leakage from intensity to polarization, | ||
| + | * a bandpass mismatch for foregrounds response due to color corrections with respect to the CMB calibration, also inducing leakage from intensity to polarization. This makes use of an input spatial template (2015 Planck component separation results) of each foreground, | ||
| + | * the absolute calibration from the orbital dipole (the kinetic dipole associated with the Earth motion around the Sun) which does not project on the sky. | ||
| + | |||
| + | The destripper is only sensitive to differences between bolometer coefficients. Thus, the absolute average value of the parameters within a frequency band is taken imposing: | ||
| + | * the sum of the offsets to be zero (no monopoles), | ||
| + | * the average of the additional color corrections (for both dust and free-free emission) to be zero, thus keeping the same average as the ground-based one. | ||
| + | . | ||
| + | |||
| + | === ''SRoll'' outputs === | ||
| + | 1. ''SRoll'' ouputs are frequency sky maps (hereafater called "primary frequency maps"). These include the Solar dipole signal (i.e. the kinetic dipole associated with the motion of the Solar system with respect to the CMB) which projects on the sky. Combining these primary maps allows to separate the different components, and extract the Solar dipole. | ||
| + | |||
| + | 2. From these primary frequency maps, the ''Planck'' 2015 Solar dipole (d,l,b)= (3364.5 ± 2.0 μK, 264.00 ± 0.03°, 48.24 ± 0.02°) is then removed leading to the delivered [[#Frequency maps|'''PR3 HFI frequency maps''']]. | ||
| + | |||
| + | 3. The HFI frequency maps, combined with the LFI ones, lead, thanks to component separation methods, to physical component maps: [[CMB_maps|'''CMB maps''']] and [[Foreground_maps|'''diffuse foregrounds maps''']]. | ||
| + | |||
| + | 4. Removing the CMB anisotropies and diffuse foreground component maps from the primary frequency maps leaves a Solar dipole signal per frequency. Ultimately, combining these maps lead to the best 2018 HFI measurement of the [[#HFI 2018 Solar dipole | '''Solar dipole parameters''']]. | ||
| + | |||
| + | Note that this is an iterative process. Ultimately, CMB analysis should combine all these steps within the same mapmaking process. | ||
| + | |||
| + | == Calibration accuracy == | ||
| + | |||
| + | The orbital dipole calibration accuracy on frequency bands can be tested using the Solar dipole. | ||
| + | |||
| + | 1. End-to-end simulations give a tool to test the biais and uncertainties induced by the Sroll processing, by comparing the Solar dipole amplitude input and output. The following numbers are extracted from Table 7 of {{PlanckPapers|planck2016-l03}}, and give, for each frequency band, this absolute frequency bias, based on 100 end-to-end simulations: | ||
| + | *at 100 GHz: 8.0 x 10<sup>-5</sup> ± 1.5 x 10<sup>-4</sup> | ||
| + | *at 143 GHz: 2.1 x 10<sup>-4</sup> ± 1.1 x 10<sup>-4</sup> | ||
| + | *at 217 GHz: 2.8 x 10<sup>-4</sup> ± 1.4 x 10<sup>-4</sup> | ||
| + | *at 353 GHz: 2.4 x 10<sup>-4</sup> ± 3.9 x 10<sup>-4</sup> | ||
| + | |||
| + | 2. The Solar dipole is obtained by removing from the primary frequency maps, the CMB anisotropies (obtained by 4 different component separation methods), and the foreground maps (dominated by dust). Uncertainties on this determination are due to residual dipoles from the CMB anisotropies removal, and from the dust removal, which are tested by the dispersion in component separation methods and along different sky fractions. The best Solar dipole determination is obtained by combining the 100, 143 and 217 GHz data. | ||
| + | |||
| + | We construct an estimate of uncertainty on the Solar dipole amplitude starting from the statistical uncertainties given, for a given sky fraction and CMB extraction, by the ''SRoll'' algorithm (0.09 μK rms), referred to as "stat". Nevertheless the dispersion observed with sky fraction and the four component separation methods is a factor an order of magnitude larger (0.91 μK). This includes both the effect of the dust residuals (traced by sky fraction) and CMB dipole removal residual (traced by the four component separation methods). Furthermore, the absolute \sroll\ bias measured on the Solar dipole is (0.64 ± 0.46)μK, referred to as "cal'" | ||
| + | |||
| + | We thus obtain the best [[#HFI 2018 Solar dipole|'''HFI 2018 Solar dipole''']] determination which gives the uncertainty on the photometric calibration. | ||
| + | |||
| + | Transfer function effects lead to an inter-calibration accuracy of the 3 CMB channels better than $1\time10^{-3}$ at the first acoustic peak, rising to $3\time10^{-3}$ at the third peak. | ||
| + | |||
| + | ==== HFI 2018 Solar dipole ==== | ||
| + | |||
| + | From the steps described above and detailled in {{PlanckPapers|planck2016-l03}}, we obtain the best HFI 2018 Solar dipole velocity vector and amplitude (which is directly obtained from the Earth orbital dipole). Note that the accuracy of the measurement depends on all steps described. We also give the amplitude in temperature, based on the CMB temperature as used in the 2015 release: | ||
| + | |||
| + | '''v = (369.8150 ± 0.0010) km s<sup>-1</sup>''' | ||
| + | |||
| + | '''A = (3362.08 ± 0.09 (stat.) ± 0.45 (syst.) ± 0.32 (cal.) μK''' | ||
| + | |||
| + | '''l = (264.021 ± 0.003 (stat.) ± 0.0079 (syst.) )°''' | ||
| + | |||
| + | '''b = (48.253 ± 0.001 (stat.) ± 0.0037 (syst.) )°''' | ||
| + | |||
| + | == Overall quality assessment == | ||
| + | Several null tests have been used (detset, hm, odd-even rings). The power spectra of the associated map differences are well reproduced by the end-to-end simulations, including all significant systematic effects. This shows that, at this level of accuracy, there is no unidentified systematics. | ||
| + | |||
| + | [[File:newpte.pdf|thumb|center|500px|'''Figure 17 of ({{PlanckPapers|planck2016-l03}}. ''']] | ||
| + | |||
| + | == Complementary figures of the HFI DPC paper == | ||
| + | |||
| + | Complementary figures of the HFI 2018 DPC paper ({{PlanckPapers|planck2016-l03}}) are given [[Appendix_of_HFI_DPC_paper| HERE]]. | ||
| + | |||
| + | == Previous Releases: (2015) and (2013) Mapmaking and photometric calibration == | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="background-color: #FFDAB9;width:80%"> | ||
| + | '''2015 Mapmaking and photometric calibration''' | ||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | '' Introduction '' | ||
| + | |||
| + | This section will give an overview of the mapmaking and photometric calibration procedures used by the HFI DPC to build detector and frequency maps for the 2015 data release. They are described in {{PlanckPapers|planck2014-a09}}. | ||
| + | These have common elements with the tools used for the 2013 release that are described in {{PlanckPapers|planck2013-p03}} and {{PlanckPapers|planck2013-p03b}}. | ||
| + | |||
| + | To build HFI maps, we use the destriping approximation, in which noise is assumed to decompose into two components, namely white noise plus low frequency drifts. Using the sky redundancy, the low frequency drifts are modelled as one constant, or offset, per pointing period. To speed up the subsequent processing we first build intermediate products, by taking advantage of redundancies. We average signal and detector orientation on HEALPix pixels visited during | ||
| + | each fixed pointing period, which we call hereafter a "ring." The detector pointing is corrected for slow drifts and aberration (displacement on the sky induced by the satellite's motion). This intermediate product is called HPR for HEALPix pixel ring." These have been constructed using the same map resolution as the final HFI products (corresponding to <i>N</i><sub>side</sub>=2048). | ||
| + | This new data set is used as input for the following steps. | ||
| + | |||
| + | '' Photometric calibration '' | ||
| + | |||
| + | ''' Dipole calibration (100 to 353 GHz) ''' | ||
| + | |||
| + | For the 2015 data release, the HFI CMB channels were calibrated using the orbital dipole modulation. This time-variable anisotropy results from the motion of the spacecraft in the solar system, which is precisely known. Thus it provides an absolute calibrator for orbital CMB missions. Its measurement is now used to calibrate HFI data, thanks to the improvements in the time stability of the data | ||
| + | brought by the ADC nonlinearity corrections and a better characterization of the time response of the detectors. | ||
| + | |||
| + | Residual time response slow components are modelled as a dipole shifted by 90° in phase, whose amplitude is fitted bolometer per bolometer. To mitigate residual systematics, we perform a simultaneous fit of the detectors gains on the orbital dipole. This amounts to solving the nonlinear equation | ||
| + | |||
| + | <math> d\ =\ g_i.(S+D) + O_i + n,\label{nlequat}</math> | ||
| + | |||
| + | where <i>d</i> is the detector measurement, <i>D</i> the total dipole component, <i>n</i> the (white) noise, and <i>S</i> the sky signal, <i>g</i> the detector gain, <i>O</i> the offset (for ring number <i>i</i>) are the unknowns to be determined. | ||
| + | This is done by linearizing the above equation to look for gains and sky variations, and iterating by updating the approximate sky and gains. | ||
| + | |||
| + | |||
| + | ''' Higher frequency calibration (545 and 857 GHz) ''' | ||
| + | |||
| + | We derived the sub-mm channels' calibration for the 2015 Planck data release from comparison of measurements of the Neptune and Uranus flux densities (using aperture photometry) with their expectations from the Moreno et al. model of their atmospheric emission. This procedure is justified, since for both planets, at the lower frequencies (100-353 GHz), the flux densities we recover are in agreement within approximately ±5% of what is expected from the planet spectral model, given the HFI detector bandpasses. | ||
| + | |||
| + | ''' Zero levels ''' | ||
| + | We determined zero-levels for the released maps in selected regions of the sky where dust emission is low and well-correlated with HI. We may thus estimate and subtract dust emission using the HI template, and CMB using a Planck component-separated template. The remaining astrophysical zero level should be that of the CIB. By imposing that the level we find is equal to that of the CIB model of Béthermin et al., we thereby set the zero level of our maps. | ||
| + | |||
| + | '' Building of maps '' | ||
| + | |||
| + | Using the photometric calibration parameters, we build maps in two steps: | ||
| + | |||
| + | * we determine the destriping offsets using the full mission data for all detectors of a given frequency; | ||
| + | * we build the maps, using these offsets, by inverting the photometric equation | ||
| + | |||
| + | <math> d_i = g(I^p+\eta [Q^p cos(2\psi_i) + U^p sin(2\psi_i)]) + n.\label{photeq}</math> | ||
| + | |||
| + | Here <i>d</i> is the destriped and calibrated signal at the HPR level. The detector data are combined with inverse noise weights derived from each detector's NEP. <i>Q</i>, and <i>U</i> maps are built whenever possible. We propagate the white noise by building the 3×3 (or 1×1 if only <i>I</i> is reconstructed) covariance matrices in each pixel. | ||
| + | At each frequency we build maps combining all detectors and independent detector sets. | ||
| + | We use the offsets built for the full mission for constructing maps for each scan survey, year (combination of Surveys 1 and 2 or 3 and 4, respectively), and for the full, nominal mission duration and its two halves. | ||
| + | We also build maps from the two independent halves of each ring. Altogether, more than 8000 maps are built at each release. | ||
| + | |||
| + | HPR and maps are built in Galactic coordinates. | ||
| + | |||
| + | '' Noise properties '' | ||
| + | |||
| + | Map noise properties can be evaluated using several methods, thanks to the high level of observational redundancy. | ||
| + | We can use the maps built from the differences between the first and second halves of each ring, or compare individual sky scans, years, half-mission or independent detector sets with each other. | ||
| + | Some of these tests are described in {{PlanckPapers|planck2014-a09}}. | ||
| + | |||
| + | Low resolution (<i>N</i><sub>side</sub> = 8, 16) pixel-to-pixel noise covariance matrices are built from the measured noise power spectra using an analytic approach. | ||
| + | |||
| + | '' Zodiacal light correction '' | ||
| + | |||
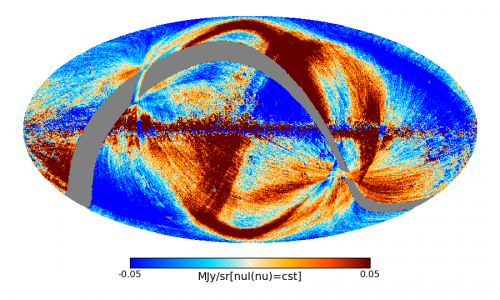
| + | At the highest Planck frequencies, zodiacal light emission is visible in a survey difference map, shown below. | ||
| + | |||
| + | [[File:Z857SurveyJackknifeWiZodi.png|500px|thumb|center|2013 Release 857-GHz Survey 2 - Survey 1 difference.]] | ||
| + | |||
| + | This map is a difference between the 857-GHz Survey 2 map and the 857-GHz Survey 1 map. This difference effectively removes Galactic and other emission that originates far from Planck. As the Solar elongation is different for measurements of the same point on the sky for the two surveys, we see zodiacal light emission, while all emission from further sources is removed. The zodiacal light emission follows the Ecliptic plane, which starts at the lower left of the image, then crosses the centre of the plot towards the upper right. Note that the "arcs" at the top and bottom of the image are images of the Galactic centre in the far sidelobes, which are discussed in the section below. Similar plots for other HFI frequencies, for maps both before and after zodiacal light removal, are shown [[beforeAndAfterSurveyDifferences|here]]. | ||
| + | |||
| + | For the 2015 Planck release, zodiacal light emission is removed from all HFI channels. The general procedure is described in {{PlanckPapers|planck2013-p03}}, but a synopsis of the procedure is as follows. | ||
| + | * During each survey, a large fraction of the sky has observations that all fall within a week of each other. That is, during a single survey, most pixels are observed during a short, well-defined period. The contribution from zodiacal light emission to the total brightness seen is then well defined. | ||
| + | * We use the the COBE model of the zodiacal light to make predictions for this emission for those pixels observed over a span of one week or less. The templates from the COBE model are shown [[COBEZodiModelTemplates|here]]. | ||
| + | * We fit the survey difference maps with these model templates to estimate the emissivity of each zodiacal light component at the Planck wavelengths. The results of these fits at each frequency are given in {{PlanckPapers|planck2014-a09}}. | ||
| + | * We reconstruct each ring of the the full mission using the combination of the COBE geometric model with the emissivities determined above. | ||
| + | * We remove the reconstruction above from each ring of data. | ||
| + | * We then make maps as described previously in this section. | ||
| + | |||
| + | '' Far SideLobes (FSL)'' | ||
| + | |||
| + | Contrary to the 2013 Planck release, far sidelobes were not removed from the HFI data for the 2015 Planck release. | ||
| + | The change of the gain due to the neglect of the far sidelobes is calculated by fitting the dipole to full timeline simulations of the dipole convolved with the FSL. The correction factors applied to the data are 0.09 % at 100 GHz, 0.05 % at 143 GHz, 0.04 % at 217 GHz and negligible at 353 GHz. Corrections were not made at 545 and 857 GHz (see {{PlanckPapers|planck2014-a09}} for details). | ||
| + | |||
| + | '' CO maps '' | ||
| + | |||
| + | Carbon monoxide rotational transition line emission is present in all HFI bands except for the 143-GHz | ||
| + | channel. It is especially significant in the 100, 217, and 353 GHz channels (due to the 115GHz | ||
| + | (1-0), 230GHz (2-1) and 345GHz (3-2) CO transitions). This emission comes essentially from | ||
| + | the Galactic interstellar medium and is mainly located at low and intermediate Galactic | ||
| + | latitudes. Three approaches (summarized below) have been used to extract CO velocity-integrated | ||
| + | emission maps from HFI data and to generate the CO products. See | ||
| + | {{PlanckPapers|planck2013-p03a}} and {{PlanckPapers|planck2014-a12}} for a full description. | ||
| + | |||
| + | *"Type 1" product: this is based on a single channel approach, using the fact that each CO | ||
| + | line has a slightly different transmission in each bolometer at a given frequency channel. | ||
| + | From this, the <i>J</i>=1-0, <i>J</i>=2-1, and <i>J</i>=3-2 CO lines can be extracted independently. Since this | ||
| + | approach is based on individual bolometer maps of a single channel, the resulting | ||
| + | S/N is relatively low. The benefit, however, is that these maps do | ||
| + | not suffer from contamination from other HFI channels (as is the case for the other | ||
| + | approaches) and are more reliable, especially in the Galactic plane. | ||
| + | |||
| + | *"Type 2" product: this product is obtained using a multi-frequency approach. Three | ||
| + | frequency channel maps are combined to extract the <i>J</i>=1-0 (using the 100, 143, and 353 | ||
| + | GHz channels) and <i>J</i>=2-1 (using the 143, 217, and 353 GHz channels) CO maps. Since | ||
| + | frequency maps are combined, the spectral behaviour of other foregrounds influences | ||
| + | the result. The two Type 2 CO maps produced in this way have a higher S/N than the | ||
| + | Type 1 maps, at the cost of a larger residual contamination from other diffuse foregrounds. | ||
| + | |||
| + | *"Type 3" product: no Type 3 product (as defined in 2013) has been produced for the | ||
| + | 2015 release. Instead, this has been is superseded by a high-resolution CO(2-1) map (FWHM=7.5') | ||
| + | produced by the Commander component separation pipeline. Note that low | ||
| + | resolution (FWHM=1°) CO maps of the three lines have also been produced using | ||
| + | Commander. See section 5 of {{PlanckPapers|planck2014-a12}} for a complete description. | ||
| + | |||
| + |
The 2015 Type 1 and Type 2 CO maps have been produced using the same procedure as | ||
| + | for the 2013 results. Very similar to their 2013 counterparts, the 2015 maps benefit from | ||
| + | an increased S/N due to the use of the full, rather than nominal, mission data. | ||
| + |
Characteristics of the released maps are the following. We provide HEALPix maps with | ||
| + | <i>N</i><sub>side</sub>=2048. For one transition, the CO velocity-integrated line signal map is given in | ||
| + | K<sub>RJ</sub> km s<sup>-1</sup> units. A conversion factor from this unit to the native unit of HFI maps (K<sub>CMB</sub>) | ||
| + | is provided in the header of the data files and in the RIMO. Four maps are given per | ||
| + | transition and per type: | ||
| + | * the signal map; | ||
| + | * the standard deviation map (same units as the signal); | ||
| + | * a null-test noise map (same units as the signal) with similar statistical properties, which is made out of half the difference of half-ring maps; | ||
| + | * a mask map (0B or 1B) giving the regions (1B) where the CO measurement is not reliable because of some severe identified foreground contamination. | ||
| + | |||
| + | All products of a given type belong to a single file. Type 1 products have the native HFI | ||
| + | resolution. i.e.. approximately 10, 5, and 5 arcmin for the CO 1-0, 2-1, and 3-2 transitions, | ||
| + | respectively. Type 2 products have a 15 arcmin resolution. | ||
| + |
We refer the reader to section 5 of {{PlanckPapers|planck2014-a12}} for a | ||
| + | description and characteristics of the Commander CO products. | ||
| + | |||
| + | '' Map validation '' | ||
| + | |||
| + | Several validations of HFI maps are described in {{PlanckPapers|planck2014-a08}} and in {{PlanckPapers|planck2014-a09}}. | ||
| + | |||
| + | Further checks are presented in the likelihood, parameters, component separation, and Commander papers. | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="background-color: #EEE8AA;width:80%"> | ||
| + | '''2013 Mapmaking and photometric calibration''' | ||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | '' Introduction '' | ||
This page will give an overview of the map-making and photometric calibration procedures used by the HFI DPC to build detector and frequency maps. | This page will give an overview of the map-making and photometric calibration procedures used by the HFI DPC to build detector and frequency maps. | ||
| Line 6: | Line 227: | ||
To build HFI maps, we use the destriping approximation, in which noise is assumed to decompose into two components : white noise plus low frequency drifts. Using the sky redundancy, the low frequency drifts are modelled as one constant, or offset, per pointing period. To speed up the ulterior processing we first build intermediate products, by taking advantage of redundancies : we average signal and detector orientation on healpix pixels visited during | To build HFI maps, we use the destriping approximation, in which noise is assumed to decompose into two components : white noise plus low frequency drifts. Using the sky redundancy, the low frequency drifts are modelled as one constant, or offset, per pointing period. To speed up the ulterior processing we first build intermediate products, by taking advantage of redundancies : we average signal and detector orientation on healpix pixels visited during | ||
| − | each fixed pointing period, which we call hereafter 'ring'. Detector's pointing are corrected for slow drifts and aberration (displacement on the sky indouced by the satellite's motion). This intermediate product is called HPR for healpix pixel ring. They have been constructed using the same map resolution as the final HFI products (corresponding to | + | each fixed pointing period, which we call hereafter 'ring'. Detector's pointing are corrected for slow drifts and aberration (displacement on the sky indouced by the satellite's motion). This intermediate product is called HPR for healpix pixel ring. They have been constructed using the same map resolution as the final HFI products (corresponding to nside=2048). |
This new dataset is used as input in the following steps. | This new dataset is used as input in the following steps. | ||
| − | + | '' Photometric calibration '' | |
| − | + | ''' Dipole calibration (100 to 353 GHz) '' | |
| − | For the 2013 data release, the calibrator for the CMB frequency was the solar dipole, as measured by the WMAP team {{BibCite|hinshaw2009}}. | + | For the 2013 data release, the calibrator for the CMB frequency was the solar dipole, as measured by the WMAP team{{BibCite|hinshaw2009}}. |
We use a two components template fitting procedure, performed for each detector independently, to determine ring by ring an estimation of the dipole gain. | We use a two components template fitting procedure, performed for each detector independently, to determine ring by ring an estimation of the dipole gain. | ||
The two fitted components are the Solar dipole and a sky template. We used the PSM for thermal dust emission at the detector's frequency as a first approximation of the sky template in pur early release. Using the HFI channel map as a template brings negligible change in the averaged gain, but reduces the systematic ring-to-ring dispersion of our estimation. We average these estimations over a subset of rings in the first survey (2000 to 6000) in which the dipole's amplitude is high enough with respect to that of the sky template, to get a single dipole gain per detector. | The two fitted components are the Solar dipole and a sky template. We used the PSM for thermal dust emission at the detector's frequency as a first approximation of the sky template in pur early release. Using the HFI channel map as a template brings negligible change in the averaged gain, but reduces the systematic ring-to-ring dispersion of our estimation. We average these estimations over a subset of rings in the first survey (2000 to 6000) in which the dipole's amplitude is high enough with respect to that of the sky template, to get a single dipole gain per detector. | ||
| Line 20: | Line 241: | ||
In the mean time we used an empiric correction, looking for a gain estimation and an offset per ring. This amounts to solve the non-linear equation : | In the mean time we used an empiric correction, looking for a gain estimation and an offset per ring. This amounts to solve the non-linear equation : | ||
| − | <math> | + | <math> d\ =\ g_i.S + O_i + n \label{nlequat}</math> |
| − | \label{nlequat}</math> | ||
where d is s the detector measurement, both S the sky signal, g the detector gain, O the offset (for ring no i) are the unknowns to be determined, and n the noise. | where d is s the detector measurement, both S the sky signal, g the detector gain, O the offset (for ring no i) are the unknowns to be determined, and n the noise. | ||
We linearized this equation starting from the constant gain approximation, to get a measurement of the apparent time-varying gains for each bolometer independently. The limitations of this process are intrinsic signal variability from one observation to the other, like polarization or intra-pixel gradient. This procedure was thus only used for the 100 to 217 GHz detectors, for which the dipole signal is brighter and galactic signal (and polarization). A mask was used to removed the inner part of the Galactic plane. | We linearized this equation starting from the constant gain approximation, to get a measurement of the apparent time-varying gains for each bolometer independently. The limitations of this process are intrinsic signal variability from one observation to the other, like polarization or intra-pixel gradient. This procedure was thus only used for the 100 to 217 GHz detectors, for which the dipole signal is brighter and galactic signal (and polarization). A mask was used to removed the inner part of the Galactic plane. | ||
| − | + | ''' Higher frequency calibration (545 and 857 GHz) ''' | |
We therefore finally derived the sub-mm channels' calibration for the 2013 Planck data release from the comparison of measurements of the Neptune and Uranus fluxes (with aperture photometry) with their expectations from the Moreno et al model of their atmospheres' emission. This procedure is justified, since for both planets, at the lower frequencies (100-353 Ghz), the fluxes we recover are in agreement within ~ +/-5\% with what is expected from the planet spectral model, and the HFI detector's band-passes. | We therefore finally derived the sub-mm channels' calibration for the 2013 Planck data release from the comparison of measurements of the Neptune and Uranus fluxes (with aperture photometry) with their expectations from the Moreno et al model of their atmospheres' emission. This procedure is justified, since for both planets, at the lower frequencies (100-353 Ghz), the fluxes we recover are in agreement within ~ +/-5\% with what is expected from the planet spectral model, and the HFI detector's band-passes. | ||
| Line 33: | Line 253: | ||
| − | + | '' Building of maps '' | |
Using the photometric calibration parameters, we build maps in two steps : | Using the photometric calibration parameters, we build maps in two steps : | ||
| Line 40: | Line 260: | ||
* we build the maps, using these offsets, by inverting the photometric equation : | * we build the maps, using these offsets, by inverting the photometric equation : | ||
| − | <math> | + | <math> d_i = g(I^p+\eta [Q^p cos(2\psi_i) + U^p sin(2\psi_i)]) + n\label{photeq}</math> |
| − | \label{photeq}</math> | ||
where d is the destriped and calibrated signal at the HPR level. Detector's data are combined with an inverse noise weights derived from each detector's NEP. Q and U maps are build whenever possible. We propagate the white noise by building the 3x3 (or 1x1 if only I is reconstructed) covariance matrices in each pixel. | where d is the destriped and calibrated signal at the HPR level. Detector's data are combined with an inverse noise weights derived from each detector's NEP. Q and U maps are build whenever possible. We propagate the white noise by building the 3x3 (or 1x1 if only I is reconstructed) covariance matrices in each pixel. | ||
At each frequency we build maps combining all detectors and independent detector sets. | At each frequency we build maps combining all detectors and independent detector sets. | ||
| Line 49: | Line 268: | ||
HPR and Maps are built in galactic coordinates. | HPR and Maps are built in galactic coordinates. | ||
| − | + | '' Noise properties '' | |
Map noise properties can be evaluated using several methods, thanks to the high level of observation redundancies. | Map noise properties can be evaluated using several methods, thanks to the high level of observation redundancies. | ||
| Line 56: | Line 275: | ||
Low resolution (nside = 8, 16, 32 ?) pixel-to-pixel noise covariance matrices are build using an analytic approach from the measured noise power spectra. | Low resolution (nside = 8, 16, 32 ?) pixel-to-pixel noise covariance matrices are build using an analytic approach from the measured noise power spectra. | ||
| − | + | '' Zodiacal light correction '' | |
At the highest Planck frequencies, zodiacal light emission is visible in a survey difference map: | At the highest Planck frequencies, zodiacal light emission is visible in a survey difference map: | ||
| Line 64: | Line 283: | ||
This map is a difference between the 857 GHz Survey 2 map and the 857 GHz Survey 1 map. This difference effectively removes Galactic and other emissions which originate far from Planck. As the Solar elongation is different for measurements of the same point on the sky for the two surveys, we see zodiacal light emission, while all emission from further sources is removed. The zodiacal light emission follows the Ecliptic plane, which starts at the lower left of the image, then crosses the center of the plot towards the upper right. Note that the "arcs" at the top and bottom of the image are images of the Galactic center in the Far Sidelobes, which are discussed in the section below. Similar plots for other HFI frequencies, for maps both before and after removal, are shown [[beforeAndAfterSurveyDifferences|here]]. | This map is a difference between the 857 GHz Survey 2 map and the 857 GHz Survey 1 map. This difference effectively removes Galactic and other emissions which originate far from Planck. As the Solar elongation is different for measurements of the same point on the sky for the two surveys, we see zodiacal light emission, while all emission from further sources is removed. The zodiacal light emission follows the Ecliptic plane, which starts at the lower left of the image, then crosses the center of the plot towards the upper right. Note that the "arcs" at the top and bottom of the image are images of the Galactic center in the Far Sidelobes, which are discussed in the section below. Similar plots for other HFI frequencies, for maps both before and after removal, are shown [[beforeAndAfterSurveyDifferences|here]]. | ||
| − | Zodiacal light emission is removed from the 353, 545 and 857 GHz channels. It is described in {{ | + | Zodiacal light emission is removed from the 353, 545 and 857 GHz channels. It is described in {{PlanckPapers|planck2013-p03}}, but a synopsis of the procedure is as follows: |
* During each survey, a large fraction of the sky has observations which all fall within a week of each other. That is, during a single survey, most pixels are observed during a short, well-defined period. The contribution from zodiacal light emission to the total brightness seen, then, is well defined. | * During each survey, a large fraction of the sky has observations which all fall within a week of each other. That is, during a single survey, most pixels are observed during a short, well-defined period. The contribution from zodiacal light emission to the total brightness seen, then, is well defined. | ||
* We use the the COBE model of the zodiacal light emission to make predictions for this zodiacal light emission for those pixels observed over a span of one week or less, and use GRASP models of the beams to predict the emission from the galaxy given our sidelobes. The templates from the COBE model are shown [[COBEZodiModelTemplates|here]]. | * We use the the COBE model of the zodiacal light emission to make predictions for this zodiacal light emission for those pixels observed over a span of one week or less, and use GRASP models of the beams to predict the emission from the galaxy given our sidelobes. The templates from the COBE model are shown [[COBEZodiModelTemplates|here]]. | ||
| Line 72: | Line 291: | ||
* We then make maps as described previously in this section. Maps with and without, as well as the differences between the two, are shown [[withAndWithoutRemoval|here]]. The survey differences before and after this removal are shown with and without zodical light emission removal [[beforeAndAfterSurveyDifferences|here]]. The power spectra of what is removed from each map is shown [[zodiCorrectionSpectra|here]]. | * We then make maps as described previously in this section. Maps with and without, as well as the differences between the two, are shown [[withAndWithoutRemoval|here]]. The survey differences before and after this removal are shown with and without zodical light emission removal [[beforeAndAfterSurveyDifferences|here]]. The power spectra of what is removed from each map is shown [[zodiCorrectionSpectra|here]]. | ||
| − | + | '' Far SideLobes (FSL)'' | |
The far sidelobe correction for the highest frequency HFI channels is described in [[Map-making#Zodi correction|the section above]]. Note that this correction is not always used, as other, CMB-specific, component separation methods have been more effective at removing the zodiacal light emission, though as this is done along with dust and other component removal, it is difficult to characterize the zodiacal light emission in this fashion. | The far sidelobe correction for the highest frequency HFI channels is described in [[Map-making#Zodi correction|the section above]]. Note that this correction is not always used, as other, CMB-specific, component separation methods have been more effective at removing the zodiacal light emission, though as this is done along with dust and other component removal, it is difficult to characterize the zodiacal light emission in this fashion. | ||
| Line 82: | Line 301: | ||
While there is one small region that might reach 20 micro-K (this happens when the secondary spillover overlaps with the Galactic center), most of the map is quite quiet. This is evidenced by the power spectrum of the above map, which is quite small. | While there is one small region that might reach 20 micro-K (this happens when the secondary spillover overlaps with the Galactic center), most of the map is quite quiet. This is evidenced by the power spectrum of the above map, which is quite small. | ||
| − | + | '' CO correction '' | |
| − | The extraction of CO maps from HFI maps is described in detail in the {{ | + | The extraction of CO maps from HFI maps is described in detail in the {{PlanckPapers|planck2013-p03a}}. The CO maps are produced by a combination of bolometer maps or frequency maps. |
| − | + | '' Map validation '' | |
| − | Several validations of HFI maps are described in {{ | + | Several validations of HFI maps are described in {{PlanckPapers|planck2013-p03}}, largely based on the analysis of the differences between half ring maps. |
ADC non-linearities induce significant differences (of order 1 micro-K_cmb) at low ell (<25) that are well reproduced by simulations including this effect. | ADC non-linearities induce significant differences (of order 1 micro-K_cmb) at low ell (<25) that are well reproduced by simulations including this effect. | ||
| Line 94: | Line 313: | ||
These checks showed that at higher multipole, half ring map differences give an estimation of the noise level in the total map that is biased low of ~0.5%. This bias is introduced by the deglitching algorithm which uses the same, eventually biased, signal estimation for the two halves of each rings. | These checks showed that at higher multipole, half ring map differences give an estimation of the noise level in the total map that is biased low of ~0.5%. This bias is introduced by the deglitching algorithm which uses the same, eventually biased, signal estimation for the two halves of each rings. | ||
| − | Further checks are presented in the {{ | + | Further checks are presented in the {{PlanckPapers|planck2013-p08}} and in {{PlanckPapers|planck2013-p01a}}. |
| + | |||
| + | |||
| + | </div> | ||
| + | </div> | ||
== References == | == References == | ||
Latest revision as of 07:44, 18 January 2019
Contents
Introduction[edit]
This section gives an overview of the mapmaking and the calibration procedures used to build the HFI maps.
- Procedures for the 2013 release is to be found in Planck-2013-VI[1] and Planck-2013-VIII[2] (see at the bottom of this page)
- Procedures for the 2015 release is to be found in Planck-2015-A08[3] (see at the bottom of this page)
- In 2016, a new procedure called SRoll has been introduced to extract, from the sky, parameters for systematics important to the mapmapking. This is achieved through a generalized polarized destriper which uses the redundancy between detectors inside a frequency band. Systematic effects producing leakages from intensity to polarization contribute strongly to this determinations. This allowed for the first time the use of large scale polarized data and the extraction of the reionization parameter. The procedure and its results are described in Planck-2016-XLVI[4].
- For the 2018 legacy release, the same SRoll procedure has been used to produce the frequency intensity and polarization maps. Planck-2020-A3[5] fully describes the procedures, the products and their characterization.
SRoll global solution[edit]
Inputs to SRoll[edit]
For the 2018 release, the TOI processing remains unchanged from the previous 2015 release (see TOI processing). As mentionned, a small cut of in the data selection (1000 pointing periods) has been done at the end of the cryogenic mission.
SRoll scheme[edit]
SRoll makes use of an extended destriper. Destriper methods have been used previously to remove baseline drifts from detector time streams, while making co-added maps of the data, by taking advantage of the redundancy in the scanning strategy. SRoll is a generalized polarized destriper which, in addition, compares all the observations of the same sky pixel by the same detector with different polarization angles, as well as by different detectors within the same frequency band. It thus fits differences between instrument parameters that minimize the difference between all polarized observations of the same sky pixel in the same frequency band. It solves consistently for:
- one offset for each pointing period,
- an empirical transfer function adding to the correction already done in the TOI processing (time constants less than 3 seconds), covering time constants up to 30 seconds,
- a CMB calibration mismatch between detectors, detected through the shift on the total kinetic dipole, between odd and even surveys, inducing leakage from intensity to polarization,
- a bandpass mismatch for foregrounds response due to color corrections with respect to the CMB calibration, also inducing leakage from intensity to polarization. This makes use of an input spatial template (2015 Planck component separation results) of each foreground,
- the absolute calibration from the orbital dipole (the kinetic dipole associated with the Earth motion around the Sun) which does not project on the sky.
The destripper is only sensitive to differences between bolometer coefficients. Thus, the absolute average value of the parameters within a frequency band is taken imposing:
- the sum of the offsets to be zero (no monopoles),
- the average of the additional color corrections (for both dust and free-free emission) to be zero, thus keeping the same average as the ground-based one.
.
SRoll outputs[edit]
1. SRoll ouputs are frequency sky maps (hereafater called "primary frequency maps"). These include the Solar dipole signal (i.e. the kinetic dipole associated with the motion of the Solar system with respect to the CMB) which projects on the sky. Combining these primary maps allows to separate the different components, and extract the Solar dipole.
2. From these primary frequency maps, the Planck 2015 Solar dipole (d,l,b)= (3364.5 ± 2.0 μK, 264.00 ± 0.03°, 48.24 ± 0.02°) is then removed leading to the delivered PR3 HFI frequency maps.
3. The HFI frequency maps, combined with the LFI ones, lead, thanks to component separation methods, to physical component maps: CMB maps and diffuse foregrounds maps.
4. Removing the CMB anisotropies and diffuse foreground component maps from the primary frequency maps leaves a Solar dipole signal per frequency. Ultimately, combining these maps lead to the best 2018 HFI measurement of the Solar dipole parameters.
Note that this is an iterative process. Ultimately, CMB analysis should combine all these steps within the same mapmaking process.
Calibration accuracy[edit]
The orbital dipole calibration accuracy on frequency bands can be tested using the Solar dipole.
1. End-to-end simulations give a tool to test the biais and uncertainties induced by the Sroll processing, by comparing the Solar dipole amplitude input and output. The following numbers are extracted from Table 7 of Planck-2020-A3[5], and give, for each frequency band, this absolute frequency bias, based on 100 end-to-end simulations:
- at 100 GHz: 8.0 x 10-5 ± 1.5 x 10-4
- at 143 GHz: 2.1 x 10-4 ± 1.1 x 10-4
- at 217 GHz: 2.8 x 10-4 ± 1.4 x 10-4
- at 353 GHz: 2.4 x 10-4 ± 3.9 x 10-4
2. The Solar dipole is obtained by removing from the primary frequency maps, the CMB anisotropies (obtained by 4 different component separation methods), and the foreground maps (dominated by dust). Uncertainties on this determination are due to residual dipoles from the CMB anisotropies removal, and from the dust removal, which are tested by the dispersion in component separation methods and along different sky fractions. The best Solar dipole determination is obtained by combining the 100, 143 and 217 GHz data.
We construct an estimate of uncertainty on the Solar dipole amplitude starting from the statistical uncertainties given, for a given sky fraction and CMB extraction, by the SRoll algorithm (0.09 μK rms), referred to as "stat". Nevertheless the dispersion observed with sky fraction and the four component separation methods is a factor an order of magnitude larger (0.91 μK). This includes both the effect of the dust residuals (traced by sky fraction) and CMB dipole removal residual (traced by the four component separation methods). Furthermore, the absolute \sroll\ bias measured on the Solar dipole is (0.64 ± 0.46)μK, referred to as "cal'"
We thus obtain the best HFI 2018 Solar dipole determination which gives the uncertainty on the photometric calibration.
Transfer function effects lead to an inter-calibration accuracy of the 3 CMB channels better than $1\time10^{-3}$ at the first acoustic peak, rising to $3\time10^{-3}$ at the third peak.
HFI 2018 Solar dipole[edit]
From the steps described above and detailled in Planck-2020-A3[5], we obtain the best HFI 2018 Solar dipole velocity vector and amplitude (which is directly obtained from the Earth orbital dipole). Note that the accuracy of the measurement depends on all steps described. We also give the amplitude in temperature, based on the CMB temperature as used in the 2015 release:
v = (369.8150 ± 0.0010) km s-1
A = (3362.08 ± 0.09 (stat.) ± 0.45 (syst.) ± 0.32 (cal.) μK
l = (264.021 ± 0.003 (stat.) ± 0.0079 (syst.) )°
b = (48.253 ± 0.001 (stat.) ± 0.0037 (syst.) )°
Overall quality assessment[edit]
Several null tests have been used (detset, hm, odd-even rings). The power spectra of the associated map differences are well reproduced by the end-to-end simulations, including all significant systematic effects. This shows that, at this level of accuracy, there is no unidentified systematics.
Complementary figures of the HFI DPC paper[edit]
Complementary figures of the HFI 2018 DPC paper (Planck-2020-A3[5]) are given HERE.
Previous Releases: (2015) and (2013) Mapmaking and photometric calibration[edit]
2015 Mapmaking and photometric calibration
Introduction
This section will give an overview of the mapmaking and photometric calibration procedures used by the HFI DPC to build detector and frequency maps for the 2015 data release. They are described in Planck-2015-A08[3]. These have common elements with the tools used for the 2013 release that are described in Planck-2013-VI[1] and Planck-2013-VIII[2].
To build HFI maps, we use the destriping approximation, in which noise is assumed to decompose into two components, namely white noise plus low frequency drifts. Using the sky redundancy, the low frequency drifts are modelled as one constant, or offset, per pointing period. To speed up the subsequent processing we first build intermediate products, by taking advantage of redundancies. We average signal and detector orientation on HEALPix pixels visited during each fixed pointing period, which we call hereafter a "ring." The detector pointing is corrected for slow drifts and aberration (displacement on the sky induced by the satellite's motion). This intermediate product is called HPR for HEALPix pixel ring." These have been constructed using the same map resolution as the final HFI products (corresponding to Nside=2048). This new data set is used as input for the following steps.
Photometric calibration
Dipole calibration (100 to 353 GHz)
For the 2015 data release, the HFI CMB channels were calibrated using the orbital dipole modulation. This time-variable anisotropy results from the motion of the spacecraft in the solar system, which is precisely known. Thus it provides an absolute calibrator for orbital CMB missions. Its measurement is now used to calibrate HFI data, thanks to the improvements in the time stability of the data brought by the ADC nonlinearity corrections and a better characterization of the time response of the detectors.
Residual time response slow components are modelled as a dipole shifted by 90° in phase, whose amplitude is fitted bolometer per bolometer. To mitigate residual systematics, we perform a simultaneous fit of the detectors gains on the orbital dipole. This amounts to solving the nonlinear equation
where d is the detector measurement, D the total dipole component, n the (white) noise, and S the sky signal, g the detector gain, O the offset (for ring number i) are the unknowns to be determined. This is done by linearizing the above equation to look for gains and sky variations, and iterating by updating the approximate sky and gains.
Higher frequency calibration (545 and 857 GHz)
We derived the sub-mm channels' calibration for the 2015 Planck data release from comparison of measurements of the Neptune and Uranus flux densities (using aperture photometry) with their expectations from the Moreno et al. model of their atmospheric emission. This procedure is justified, since for both planets, at the lower frequencies (100-353 GHz), the flux densities we recover are in agreement within approximately ±5% of what is expected from the planet spectral model, given the HFI detector bandpasses.
Zero levels We determined zero-levels for the released maps in selected regions of the sky where dust emission is low and well-correlated with HI. We may thus estimate and subtract dust emission using the HI template, and CMB using a Planck component-separated template. The remaining astrophysical zero level should be that of the CIB. By imposing that the level we find is equal to that of the CIB model of Béthermin et al., we thereby set the zero level of our maps.
Building of maps
Using the photometric calibration parameters, we build maps in two steps:
- we determine the destriping offsets using the full mission data for all detectors of a given frequency;
- we build the maps, using these offsets, by inverting the photometric equation
Here d is the destriped and calibrated signal at the HPR level. The detector data are combined with inverse noise weights derived from each detector's NEP. Q, and U maps are built whenever possible. We propagate the white noise by building the 3×3 (or 1×1 if only I is reconstructed) covariance matrices in each pixel. At each frequency we build maps combining all detectors and independent detector sets. We use the offsets built for the full mission for constructing maps for each scan survey, year (combination of Surveys 1 and 2 or 3 and 4, respectively), and for the full, nominal mission duration and its two halves. We also build maps from the two independent halves of each ring. Altogether, more than 8000 maps are built at each release.
HPR and maps are built in Galactic coordinates.
Noise properties
Map noise properties can be evaluated using several methods, thanks to the high level of observational redundancy. We can use the maps built from the differences between the first and second halves of each ring, or compare individual sky scans, years, half-mission or independent detector sets with each other. Some of these tests are described in Planck-2015-A08[3].
Low resolution (Nside = 8, 16) pixel-to-pixel noise covariance matrices are built from the measured noise power spectra using an analytic approach.
Zodiacal light correction
At the highest Planck frequencies, zodiacal light emission is visible in a survey difference map, shown below.
This map is a difference between the 857-GHz Survey 2 map and the 857-GHz Survey 1 map. This difference effectively removes Galactic and other emission that originates far from Planck. As the Solar elongation is different for measurements of the same point on the sky for the two surveys, we see zodiacal light emission, while all emission from further sources is removed. The zodiacal light emission follows the Ecliptic plane, which starts at the lower left of the image, then crosses the centre of the plot towards the upper right. Note that the "arcs" at the top and bottom of the image are images of the Galactic centre in the far sidelobes, which are discussed in the section below. Similar plots for other HFI frequencies, for maps both before and after zodiacal light removal, are shown here.
For the 2015 Planck release, zodiacal light emission is removed from all HFI channels. The general procedure is described in Planck-2013-VI[1], but a synopsis of the procedure is as follows.
- During each survey, a large fraction of the sky has observations that all fall within a week of each other. That is, during a single survey, most pixels are observed during a short, well-defined period. The contribution from zodiacal light emission to the total brightness seen is then well defined.
- We use the the COBE model of the zodiacal light to make predictions for this emission for those pixels observed over a span of one week or less. The templates from the COBE model are shown here.
- We fit the survey difference maps with these model templates to estimate the emissivity of each zodiacal light component at the Planck wavelengths. The results of these fits at each frequency are given in Planck-2015-A08[3].
- We reconstruct each ring of the the full mission using the combination of the COBE geometric model with the emissivities determined above.
- We remove the reconstruction above from each ring of data.
- We then make maps as described previously in this section.
Far SideLobes (FSL)
Contrary to the 2013 Planck release, far sidelobes were not removed from the HFI data for the 2015 Planck release. The change of the gain due to the neglect of the far sidelobes is calculated by fitting the dipole to full timeline simulations of the dipole convolved with the FSL. The correction factors applied to the data are 0.09 % at 100 GHz, 0.05 % at 143 GHz, 0.04 % at 217 GHz and negligible at 353 GHz. Corrections were not made at 545 and 857 GHz (see Planck-2015-A08[3] for details).
CO maps
Carbon monoxide rotational transition line emission is present in all HFI bands except for the 143-GHz channel. It is especially significant in the 100, 217, and 353 GHz channels (due to the 115GHz (1-0), 230GHz (2-1) and 345GHz (3-2) CO transitions). This emission comes essentially from the Galactic interstellar medium and is mainly located at low and intermediate Galactic latitudes. Three approaches (summarized below) have been used to extract CO velocity-integrated emission maps from HFI data and to generate the CO products. See Planck-2013-XIII[6] and Planck-2015-A10[7] for a full description.
- "Type 1" product: this is based on a single channel approach, using the fact that each CO
line has a slightly different transmission in each bolometer at a given frequency channel. From this, the J=1-0, J=2-1, and J=3-2 CO lines can be extracted independently. Since this approach is based on individual bolometer maps of a single channel, the resulting S/N is relatively low. The benefit, however, is that these maps do not suffer from contamination from other HFI channels (as is the case for the other approaches) and are more reliable, especially in the Galactic plane.
- "Type 2" product: this product is obtained using a multi-frequency approach. Three
frequency channel maps are combined to extract the J=1-0 (using the 100, 143, and 353 GHz channels) and J=2-1 (using the 143, 217, and 353 GHz channels) CO maps. Since frequency maps are combined, the spectral behaviour of other foregrounds influences the result. The two Type 2 CO maps produced in this way have a higher S/N than the Type 1 maps, at the cost of a larger residual contamination from other diffuse foregrounds.
- "Type 3" product: no Type 3 product (as defined in 2013) has been produced for the
2015 release. Instead, this has been is superseded by a high-resolution CO(2-1) map (FWHM=7.5') produced by the Commander component separation pipeline. Note that low resolution (FWHM=1°) CO maps of the three lines have also been produced using Commander. See section 5 of Planck-2015-A10[7] for a complete description.
The 2015 Type 1 and Type 2 CO maps have been produced using the same procedure as for the 2013 results. Very similar to their 2013 counterparts, the 2015 maps benefit from an increased S/N due to the use of the full, rather than nominal, mission data. Characteristics of the released maps are the following. We provide HEALPix maps with Nside=2048. For one transition, the CO velocity-integrated line signal map is given in KRJ km s-1 units. A conversion factor from this unit to the native unit of HFI maps (KCMB) is provided in the header of the data files and in the RIMO. Four maps are given per transition and per type:
- the signal map;
- the standard deviation map (same units as the signal);
- a null-test noise map (same units as the signal) with similar statistical properties, which is made out of half the difference of half-ring maps;
- a mask map (0B or 1B) giving the regions (1B) where the CO measurement is not reliable because of some severe identified foreground contamination.
All products of a given type belong to a single file. Type 1 products have the native HFI resolution. i.e.. approximately 10, 5, and 5 arcmin for the CO 1-0, 2-1, and 3-2 transitions, respectively. Type 2 products have a 15 arcmin resolution. We refer the reader to section 5 of Planck-2015-A10[7] for a description and characteristics of the Commander CO products.
Map validation
Several validations of HFI maps are described in Planck-2015-A07[8] and in Planck-2015-A08[3].
Further checks are presented in the likelihood, parameters, component separation, and Commander papers.
2013 Mapmaking and photometric calibration
Introduction
This page will give an overview of the map-making and photometric calibration procedures used by the HFI DPC to build detector and frequency maps. This processing and its performances are described in Planck-2013-VI[1] and Planck-2013-VIII[2].
To build HFI maps, we use the destriping approximation, in which noise is assumed to decompose into two components : white noise plus low frequency drifts. Using the sky redundancy, the low frequency drifts are modelled as one constant, or offset, per pointing period. To speed up the ulterior processing we first build intermediate products, by taking advantage of redundancies : we average signal and detector orientation on healpix pixels visited during each fixed pointing period, which we call hereafter 'ring'. Detector's pointing are corrected for slow drifts and aberration (displacement on the sky indouced by the satellite's motion). This intermediate product is called HPR for healpix pixel ring. They have been constructed using the same map resolution as the final HFI products (corresponding to nside=2048). This new dataset is used as input in the following steps.
Photometric calibration
' Dipole calibration (100 to 353 GHz)
For the 2013 data release, the calibrator for the CMB frequency was the solar dipole, as measured by the WMAP team[9]. We use a two components template fitting procedure, performed for each detector independently, to determine ring by ring an estimation of the dipole gain. The two fitted components are the Solar dipole and a sky template. We used the PSM for thermal dust emission at the detector's frequency as a first approximation of the sky template in pur early release. Using the HFI channel map as a template brings negligible change in the averaged gain, but reduces the systematic ring-to-ring dispersion of our estimation. We average these estimations over a subset of rings in the first survey (2000 to 6000) in which the dipole's amplitude is high enough with respect to that of the sky template, to get a single dipole gain per detector.
Several pieces of evidence led us to the conclusion that out bolometers presented apparent gain variation with time, after comparing the 3rd scan of the sky with the first one. This was later (mid-2012) explained by inequalities in the steps of the analog-to-digital converters (ADC) used in each bolometer's electronic chain. These devices had to be characterized using warm data after the end of the HFI observations. This process is still on-going (01/2012).
In the mean time we used an empiric correction, looking for a gain estimation and an offset per ring. This amounts to solve the non-linear equation :
where d is s the detector measurement, both S the sky signal, g the detector gain, O the offset (for ring no i) are the unknowns to be determined, and n the noise. We linearized this equation starting from the constant gain approximation, to get a measurement of the apparent time-varying gains for each bolometer independently. The limitations of this process are intrinsic signal variability from one observation to the other, like polarization or intra-pixel gradient. This procedure was thus only used for the 100 to 217 GHz detectors, for which the dipole signal is brighter and galactic signal (and polarization). A mask was used to removed the inner part of the Galactic plane.
Higher frequency calibration (545 and 857 GHz)
We therefore finally derived the sub-mm channels' calibration for the 2013 Planck data release from the comparison of measurements of the Neptune and Uranus fluxes (with aperture photometry) with their expectations from the Moreno et al model of their atmospheres' emission. This procedure is justified, since for both planets, at the lower frequencies (100-353 Ghz), the fluxes we recover are in agreement within ~ +/-5\% with what is expected from the planet spectral model, and the HFI detector's band-passes.
We determined zero-level for the released maps is selected regions of the sky where dust emissions are low and well correlated with HI. We may thus estimate and subtract dust emissions using the Hi template, and CMB from a Planck component separated template. The remaining astrophysical zero level is that of CIB. By imposing that the vele we find is equal to that of the CIB model of Bethermin et al, we may aset the sezo level of our maps.
Building of maps
Using the photometric calibration parameters, we build maps in two steps :
- we determine the destriping offsets using the full mission data
- we build the maps, using these offsets, by inverting the photometric equation :
where d is the destriped and calibrated signal at the HPR level. Detector's data are combined with an inverse noise weights derived from each detector's NEP. Q and U maps are build whenever possible. We propagate the white noise by building the 3x3 (or 1x1 if only I is reconstructed) covariance matrices in each pixel. At each frequency we build maps combining all detectors and independent detector sets. We use the offsets build for the full mission for building maps for each scan survey and for the nominal mission duration. We also build maps from the two independent halves of each rings. Altogether, more than 6000 maps are built at each release.
HPR and Maps are built in galactic coordinates.
Noise properties
Map noise properties can be evaluated using several methods, thanks to the high level of observation redundancies. We can use the maps built from the difference between the first and second half of each rings, or compare individual sky scans, of detector sets with each other.
Low resolution (nside = 8, 16, 32 ?) pixel-to-pixel noise covariance matrices are build using an analytic approach from the measured noise power spectra.
Zodiacal light correction
At the highest Planck frequencies, zodiacal light emission is visible in a survey difference map:
This map is a difference between the 857 GHz Survey 2 map and the 857 GHz Survey 1 map. This difference effectively removes Galactic and other emissions which originate far from Planck. As the Solar elongation is different for measurements of the same point on the sky for the two surveys, we see zodiacal light emission, while all emission from further sources is removed. The zodiacal light emission follows the Ecliptic plane, which starts at the lower left of the image, then crosses the center of the plot towards the upper right. Note that the "arcs" at the top and bottom of the image are images of the Galactic center in the Far Sidelobes, which are discussed in the section below. Similar plots for other HFI frequencies, for maps both before and after removal, are shown here.
Zodiacal light emission is removed from the 353, 545 and 857 GHz channels. It is described in Planck-2013-VI[1], but a synopsis of the procedure is as follows:
- During each survey, a large fraction of the sky has observations which all fall within a week of each other. That is, during a single survey, most pixels are observed during a short, well-defined period. The contribution from zodiacal light emission to the total brightness seen, then, is well defined.
- We use the the COBE model of the zodiacal light emission to make predictions for this zodiacal light emission for those pixels observed over a span of one week or less, and use GRASP models of the beams to predict the emission from the galaxy given our sidelobes. The templates from the COBE model are shown here.
- We fit the survey difference maps with these model templates to estimate the emissivity of each zodi component and sidelobe at the Planck wavelengths. The results of these fits at each frequency are shown here.
- We reconstruct each ring of the the full mission using the combination of the COBE geometric model with the emissivities determined above and the sidelobe models.
- We remove the reconstruction above from each ring of data.
- We then make maps as described previously in this section. Maps with and without, as well as the differences between the two, are shown here. The survey differences before and after this removal are shown with and without zodical light emission removal here. The power spectra of what is removed from each map is shown here.
Far SideLobes (FSL)
The far sidelobe correction for the highest frequency HFI channels is described in the section above. Note that this correction is not always used, as other, CMB-specific, component separation methods have been more effective at removing the zodiacal light emission, though as this is done along with dust and other component removal, it is difficult to characterize the zodiacal light emission in this fashion.
Fit values for specific horns and surveys are show here
We have made estimates of the contamination of the far sidelobes at 143 GHz by taking the 143 GHz map, adding the dipole, and passing it through our simulator, using a GRASP calculation of the far sidelobes for the 143-1a detector as the beam. The resulting maps is
While there is one small region that might reach 20 micro-K (this happens when the secondary spillover overlaps with the Galactic center), most of the map is quite quiet. This is evidenced by the power spectrum of the above map, which is quite small.
CO correction
The extraction of CO maps from HFI maps is described in detail in the Planck-2013-XIII[6]. The CO maps are produced by a combination of bolometer maps or frequency maps.
Map validation
Several validations of HFI maps are described in Planck-2013-VI[1], largely based on the analysis of the differences between half ring maps.
ADC non-linearities induce significant differences (of order 1 micro-K_cmb) at low ell (<25) that are well reproduced by simulations including this effect.
These checks showed that at higher multipole, half ring map differences give an estimation of the noise level in the total map that is biased low of ~0.5%. This bias is introduced by the deglitching algorithm which uses the same, eventually biased, signal estimation for the two halves of each rings.
Further checks are presented in the Planck-2013-XV[10] and in Planck-2013-XXXI[11].
References[edit]
- ↑ 1.01.11.21.31.41.5 Planck 2013 results. VI. High Frequency Instrument Data Processing, Planck Collaboration, 2014, A&A, 571, A6.
- ↑ 2.02.12.2 Planck 2013 results. VIII. HFI photometric calibration and Map-making, Planck Collaboration, 2014, A&A, 571, A8.
- ↑ 3.03.13.23.33.43.5 Planck 2015 results. VIII. High Frequency Instrument data processing: Calibration and maps, Planck Collaboration, 2016, A&A, 594, A8.
- ↑ Planck intermediate results. XLVI. Reduction of large-scale systematic effects in HFI polarization maps and estimation of the reionization optical depth, Planck Collaboration Int. XLVI A&A, 596, A107, (2016).
- ↑ 5.05.15.25.35.4 Planck 2018 results. III. High Frequency Instrument data processing and frequency maps, Planck Collaboration, 2020, A&A, 641, A3.
- ↑ 6.06.1 Planck 2013 results. XIII. Galactic CO emission, Planck Collaboration, 2014, A&A, 571, A13.
- ↑ 7.07.17.2 Planck 2015 results. X. Diffuse component separation: Foreground maps, Planck Collaboration, 2016, A&A, 594, A10.
- ↑ Planck 2015 results. VII. High Frequency Instrument data processing: Time-ordered information and beam processing, Planck Collaboration, 2016, A&A, 594, A7.
- ↑ Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Data Processing, Sky Maps, and Basic Results, G. Hinshaw, J. L. Weiland, R. S. Hill, N. Odegard, D. Larson, C. L. Bennett, J. Dunkley, B. Gold, M. R. Greason, N. Jarosik, E. Komatsu, M. R. Nolta, L. Page, D. N. Spergel, E. Wollack, M. Halpern, A. Kogut, M. Limon, S. S. Meyer, G. S. Tucker, E. L. Wright, ApJS, 180, 225-245, (2009).
- ↑ Planck 2013 results. XV. CMB power spectra and likelihood, Planck Collaboration, 2014, A&A, 571, A15.
- ↑ Planck 2013 results. XXXI. Consistency of Planck data, Planck Collaboration, 2014, A&A, 571, A31.
(Planck) High Frequency Instrument
Cosmic Microwave background
(Planck) Low Frequency Instrument
Data Processing Center
(Hierarchical Equal Area isoLatitude Pixelation of a sphere, <ref name="Template:Gorski2005">HEALPix: A Framework for High-Resolution Discretization and Fast Analysis of Data Distributed on the Sphere, K. M. Górski, E. Hivon, A. J. Banday, B. D. Wandelt, F. K. Hansen, M. Reinecke, M. Bartelmann, ApJ, 622, 759-771, (2005).
analog to digital converter
Noise Equivalent Power
Full-Width-at-Half-Maximum
reduced IMO
Planck Sky Model