HFI detection chain

Bolometers

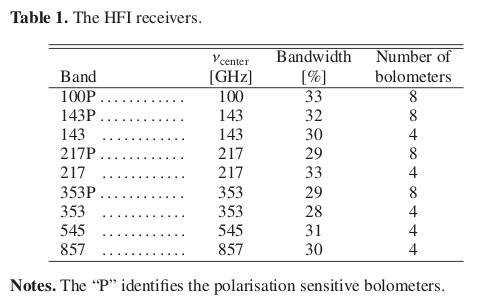
The heart of the HFI - the detectors - are bolometers, solid-state devices in which the incoming radiation dissipates its energy as heat that increases the temperature of a thermometer. The instrument Flight Model total number of bolometers is 52, split into 6 channels at central frequencies of 100, 143, 217, 353, 545, and 857GHz. Two extra bolometers not optically coupled to the telescope are added to the focal plane to monitor thermal noise (Dark Bolometers).

Thirty two of these bolometers are polarization sensitive allowing a map of the CMB polarisation to be built.

Bolometers consist of (i) an absorber that transforms the in-coming radiation into heat; (ii) a thermometer that is thermally linked to the absorber and measures the temperature changes; and (iii) a weak thermal link to a thermal sink, to which the bolometer is attached.

The detectors are semi-conducting NTD thermistor bolometers. There are two kinds of detector modules:

• SWB, spider web bolometers, are mounted on an absorbing spider-web of metallised silicon nitride
• PSB, polarization sensitive bolometers, are mounted or on a parallel absorbing grid of metallised silicon nitride.

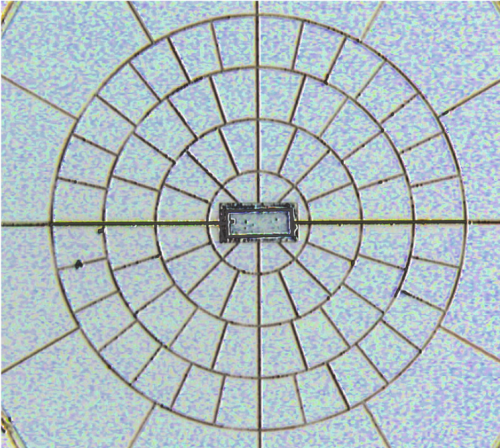
In the spider-web bolometers, or SWBs (Bock et al. 1995; Mauskopf et al. 1997), the absorbers consist of metallic grids deposited on a Si3 N4 substrate in the shape of a spider web. The mesh design and the impedance of the metallic layer are adjusted to match vacuum impedance and maximize the absorption of millimeter waves, while minimizing the cross section to particles. The absorber is designed to offer equal impedance to any linearly polarised radiation. Nevertheless, the thermometer and its electrical leads define a privileged orientation (Fig. SWB) that makes the SWBs slightly sensitive to polarisation, as detailed in (Rosset et al. 2010). The thermometers are made of neutron transmuted doped (NTD) germanium (Haller et al. 1996), chosen to have an impedance of about 10 MΩ at their operating temperature.

Picture of a spider web bolometer. This a 143 GHz module, The temperature sensor is at the center of the absorbing grid

The absorber of PSBs is a rectangular grid (Fig. PSB) with metallization in one direction (Jones et al. 2003). Electrical fields parallel to this direction develop currents and then deposit some power in the grid, while perpendicular electrical fields propagate through the grid without significant interaction. A second PSB perpendicular to the first one absorbs the other polarisation. Such a PSB pair measures two polarisations of radiation collected by the same horns and filtered by the same devices, which minimises the systematic effects: differences between polarised beams collected by a given horn are typically less than −30 dB of the peak. The differences in the spectral responses of a PSB pair also proved to be a few percent in the worst case. Each pair of PSBs sharing the same horn is able to measure the intensity Stokes parameter and the Q parameter associated with its local frame. An associated pair of PSBs rotated by 45◦ scans exactly the same line (if the geometrical alignment is perfect), providing the U Stokes parameter.

Picture of a polarization sensitive bolometer. This a 217 GHz module, The temperature sensor is at the an edge of the absorbing grid

The detectors operate at a temperature close to 100 mK, while the filters are distributed on the 100mK, 1.6 K, and 4 K stages in such a way that the heat load on the coldest stages is minimized to limit the heat load on the detectors and to decrease the heat lift requirement and thus enhance the mission lifetime. The self-emission of the 4K stage is minimised to limit the photon noise contribution on the detectors from the instrument. The HFI Focal Plane Unit accommodates sub-millimiter absorbing material in order to decrease the scattering inside it.

to be change into a real table

Focal plane layout

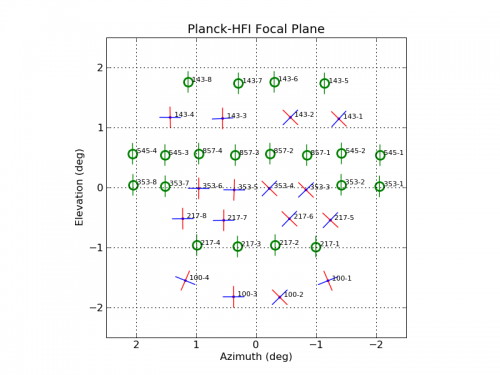
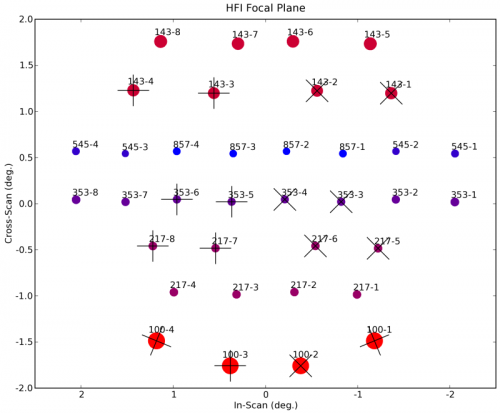
The layout of the detectors in the focal plane is defined to cope with the scanning strategy. The HFI horns are positioned at the centre of the focal plane, where the optical quality is good enough for the high frequencies. The curvature of rows compensates for the distortion of images by the telescope. A pair of identical SWB will scan the same circle on the sky to provide additional redundancy. Similar horns feeding PSBs are also aligned so that two pairs of PSBs rotated by 45◦ with respect to each other scan the same line. This will provide the Q and U Stokes parameters with minimal correction for the pointing (Rosset et al. 2010). Residual systematics will come from the differences between the beam shapes of the two horns. In all cases except for the 100 GHz horns, a measurement is also done by a pair of similar channels shifted by 1.25 arcminutes in the cross-scan direction, to ensure adequate sampling. In the figures focal plane layout is reported.

Focal plane layout as seen from outside the celestial sphere. Each spot represents an horn in the focal plane. Coordinates are in pointing direction with respect to the telescope boresight. PSBs detectors are indicated with a cross oriented as the two polarimeters axes. Scan direction is from left to right.

Focal plane layout as seen from outside the celestial sphere. In this case PSBs orientations are reported. Red rod is for a elements of PSBs, blue rod is for b elements.

Readout

The AC bias readout electronics of the HFI instrument (Gaertner et al. 1997) includes a number of original features proposed by several laboratories (CRTBT in Grenoble, CESR in Toulouse and IAS in Orsay), which were validated on the Diabolo experiment and on the balloon-borne Archeops experiment. It was developed for space by the CESR in Toulouse.

The particular features of the HFI AC bias readout are mainly

• i)that the cold load resistors were replaced by capacitors because they have no Johnson noise;
• ii)that the detectors are biased by applying a triangular voltage to the load capacitors

which produces a square current [Ibias ] in the capacitors, and a square voltage [T bias ] that compensates for the stray capacitance of the wiring (producing a nearly square bias current into the bolometer;

• iii)that a square offset com-pensation signal is subtracted to the bolometric signal to minimise the amplitude of the signal that has to be amplified and digitized;
• iv)that the electronic scheme is symmetrical and uses a differential amplification scheme to optimize the immunity to electromagnetic interferences;
• v)and finally that every parameter of the REU can be set by commands, which

is made possible by using digital-to-analog and analog-to-digital converters extensively.

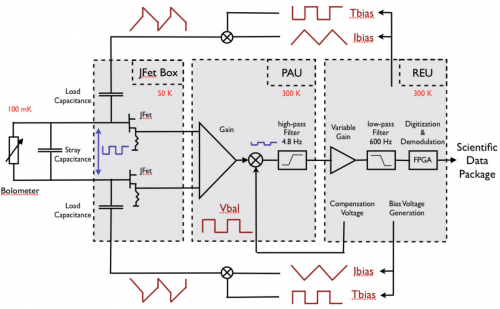
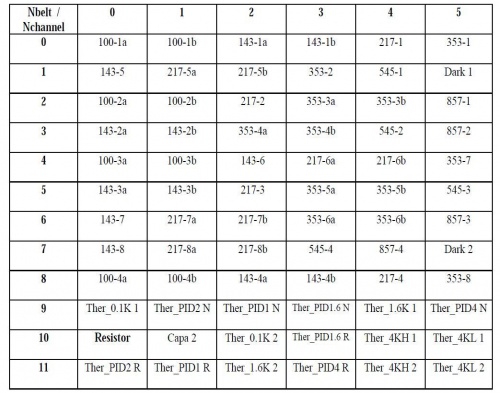
The readout electronics consist of 72 channels designed to perform low noise measurements of the impedance of 52 bolometers, two blind bolometers, 16 accurate low temperature thermometers, all in the 10 MΩ range, one resistor of 10 MΩ and one capacitor of 100 pF. The semiconductor bolometers and thermometers of Planck-HFI operate at cryogenic temperature around 100 mK on the focal plane, with impedance of about 10 MΩ when biased at the optimal current. The readout electronics on the contrary have to operate at “room” temperature (300 K). The distance between the two extremities of the readout chain is about 10 m and could represent a point of extreme susceptibility to electromagnetic interference. The readout electronic chain was split into three boxes. These are the JFET box, located on the 50 K stage of the satellite at 2.2 m from the focal plane, the pre-amplifier unit (PAU), located 1.8m further at 300 K, and the REU, located on the opposite side of the satellite, 5 m away. Each of the three boxes (JFET, PAU and REU) consists of 12 belts of six channels. The first nine belts are dedicated to the bolometers, and the three last ones to the accurate thermometers, the resistor and the capacitor (see figure Organization of the HFI readout).

Principles of readout electronics. The three modules of the chain are shown: JFet Box, Pre-Amplifier Unit (PAU) and Readout Electronic Unit (REU)

Organization of the HFI readout. Each row represents a belt. Each belt has 6 channels. (to be change into a real table ?)

Principles of the readout electronics

See figure [Principles of readout electronics]. The bolometer is biased by a square wave AC current obtained by the differentiation of a triangular voltage through a load capacitance, in a completely differential architecture. The presence of the stray capacitance due to losses of charge in the wiring requires a correction of the shape of the square bias current by a transient voltage. Thus the bias voltage generation is controlled by the two parameters I-bias and T-bias that express the amplitude of the triangular and transient voltage. The compensation voltage added to the bolometric signal to optimize the dynamic of the chain is controlled by the V-bal parameter.

Parameters of the Readout Unit can be set to optimize the detectors performance.

The modulation frequency of the AC bias system, fmod of the square bias current can be tuned from 70 Hz to 112 Hz by the telecommand parameters: Nsample, which defines the number of samples per half period of modulated signal, fdiv which determines the sampling frequency of the ADC.

The optimal frequencies are around 90 Hz.

Each channel has its own settings for the following parameters: I-bias, amplitude of the triangular bias voltage;

T-bias, amplitude of the transient bias voltage;

V-bal, amplitude of the square compensation voltage;

G-amp, value of the programmable gain of the REU [1/3, 1, 3, 7.6];

N-blank, number of blanked samples at the beginning of halfperiod not taken into account during integration of the signal;

S-phase, phase shift when computing the integrated signal.

All these parameters influence the effective response of the detection chains, and were optimized during the calibration campaigns and confirmed during the calibration and performance verification (CPV) phase following the launch of Planck. The scientific signal is provided by the integral of the signal on each half-period, between limits fixed by the S-phase and N-blank parameters.

The interaction of modulated readout electronics with semiconductor bolometers is rather different from that of a classical DC bias readout (Jones 1953). The differences were seen during the calibration of the HFI, although the readout electronics was designed to mimic the operation of a DC biased bolometric system as far as possible. With the AC readout the maximum of responsivity is lower and is obtained for higher bias current in the bolometer with respect to the DC model. This is caused by the stray capacitance in the wiring which has negligible effects for a DC bias and a major effect for an AC bias. In our case, a stray capacitance of 150 pF induces increases of NEP ranging from 4% (857 GHz bolometers) to 10% (100 GHz bolometers) and also affects the HFI time response. Details of the effect of the HFI AC bias system into the time response of the detectors are discussed in the Time Response Section.

JFETs

Given the high impedance of the bolometers and the length of the connecting cables, it it is essential that the impedance of the signal is lowered as close as possible to the detectors. In our system this is accomplished by means of JFET source followers, located in boxes connected to the 50 K stage. The JFET box has been designed, developed and tested in the Observational Cosmology group in the Physics Department of the University of Rome "La Sapienza" (Brienza D. et al 2006). There are two JFETs per channel, since the readout is fully differential, and they provide a current amplification of the signal while keeping the voltage amplification very close to unity.

Inside the box, the JFETs are mounted on a thermally insulated plate with an active temperature control to keep them at the optimal temperature of 110 K. With a dissipated power lower than 240 mW, mainly produced by the JFETs and the source resistors, we obtained a noise power spectral density of less than 3 nV Hz1/2 for the frequency range of interest. This increases the total noise ofall bolometer channels by less than 5%.

Data compression

Data compression scheme

The output of the readout electronics unit (REU) consists of one value for each of the 72 science channels (bolometers and thermometers) for each modulation half-period. This number, [math]S_{REU}[/math], is the sum of the 40 16-bit ADC signal values measured within the given half-period. The data processor unit (DPU) performs a lossy quantization of [math]S_{REU}[/math].

We define a compression slice of 254 [math]S_{REU}[/math] values, corresponding to about 1.4 s of observation for each detector and to a strip on the sky about 8 degrees long. The mean [math]\langle S_{REU} \rangle[/math] of the data within each compression slice is computed, and data are demodulated using this mean:

[math]S_{demod,i} = (S_{REU,i} - \langle S_{REU} \rangle) \ast(-)^{i}[/math]

where [math]1 \lt i \lt 254[/math] is the running index within the compression slice.

The mean [math]\langle S_{demod} \rangle[/math] of the demodulated data [math]S_{demod,i}[/math] is computed and subtracted, and the resulting slice data is quantized according to a step size Q that is fixed per detector:

[math] S_{DPU,i} = \mbox{round} \left[( S_{demod,i} - \langle S_{demod} \rangle) /Q \right ] [/math]

This is the lossy part of the algorithm: the required compression factor, obtained through the tuning of the quantization step Q, adds a noise of variance [math] \simeq 2\% [/math] to the data. This will be discussed below.

The two means [math]\langle S_{REU} \rangle[/math] and [math]\langle S_{demod} \rangle[/math] are computed as 32-bit words and sent through the telemetry, together with the [math]S_{DPU,i}[/math] values. Variable-length encoding of the [math]S_{DPU,i}[/math] values is performed on board, and the inverse decoding is applied on ground.

Performance of the data compression during the mission

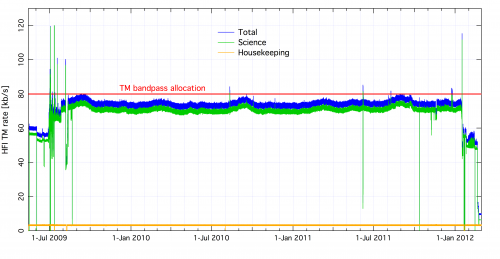
Optimal use of the bandpass available for the downlink was obtained initially by using a value of Q = [math]\sigma[/math]/2.5 for all bolometer signals. After the 12th of December 2009, and only for the 857 GHz detectors, the value was reset to Q = [math]\sigma[/math]/2.0 to avoid data loss due to exceeding the limit of the downlink rate. With these settings the load during the mission never exceeded the allowed band-pass width as is seen on the next figure.

Evolution of the total load during the mission for the 72 HFI channels. The variations are mainly due to the time spent by the high-frequency channels in the Galactic region, which has very large data gradients, and depends on the satellite scanning strategy. The bandpass-width limit was 80kb/s and was never reached during the mission.

Setting the quantization step in flight

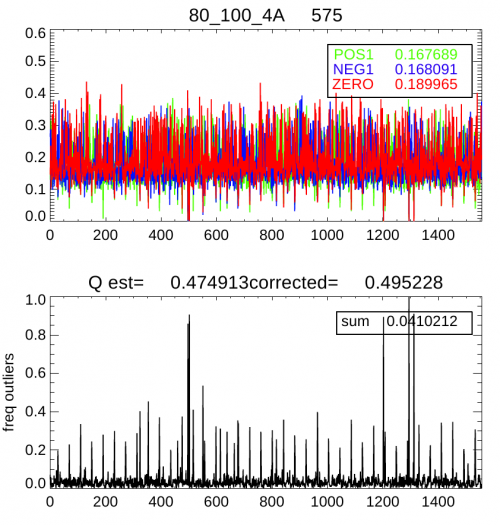
The only parameter that enters the PLANCK-HFI compression algorithm is the size of the quantization step, in units of [math]\sigma[/math], the white noise standard deviation for each channel. It has been adjusted during the mission by studying the mean frequency of the central quantization bin [-Q/2,Q/2], [math]p_0[/math] within each compression slice (254 samples). For a pure Gaussian noise, this frequency is related to the step size (in units of [math]\sigma[/math]) by [math] \hat Q =2\sqrt{2} \text{Erf}^{-1}(p_0)\simeq 2.5 p_0 [/math] where the approximation is valid up to [math]p_0 \lt 0.4[/math]. In PLANCK however the channel signal is not a pure Gaussian, since glitches and the periodic crossing of the Galactic plane add some strong outliers to the distribution. By using the frequency of these outliers, [math]p_\text{out}[/math], above [math]5 \sigma[/math], simulations show that the following formula gives a valid estimate: [math] \hat Q_\text{cor}=2.5 \frac{p_0}{1-p_\text{out}} [/math]

The following figure shows an example of the [math]\hat Q[/math] and [math]\hat Q_\text{cor}[/math] timelines that were used to monitor and adjust the quantization setting.

Example of the "bin0" frequency timeline (1 point per compression slice) [math]p_0[/math] (labeled "ZERO") for one of the channels. The -1 ("NEG1") and +1 ("POS1") bin frequencies are also shown. The lower plot shows the frequency timeline of outliers, where the glitches and periodic crossing of the Galaxy are visible. The estimated raw step size [math]\hat Q=0.47[/math] and corrected value [math]\hat Q_\text{cor}=0.49[/math] are automatically computed and the step size can be adjusted according to these control plots.

Impact of the data compression on science

The effect of a pure quantization process of step [math]Q[/math] (in units of [math]\sigma[/math]) on the statistical moments of a signal is well known (#widrow) When the step is typically below the noise level (which is largely the PLANCK case) one can apply the Quantization Theorem which states that the process is equivalent to the addition of a uniform random noise in the [math][-Q/2,Q/2][/math] range. The net effect of quantization is therefore to add quadratically to the signal a [math]Q^2/12[/math] variance. For [math]Q\simeq 0.5[/math] this corresponds to a [math]2\%[/math] noise level increase. The spectral effect of the non-linear quantization process is theoretically much more complicated and depends on the signal and noise details. As a rule of thumb, a pure quantization adds some auto-correlation function that is suppressed by a [math]\exp[-4\pi^2(\frac{\sigma}{Q})^2][/math] factor #banta. Note however that PLANCK does not perform a pure quantization process. A baseline which depends on the data (mean of each compression slice value), is subtracted. Furthermore, for the science data, circles on the sky are coadded. Coaddition is again performed when projecting the rings onto the sky (map-making). To study the full effect of the PLANCK-HFI data compression algorithm on our main science products, we have simulated a realistic data timeline corresponding to the observation of a pure CMB sky. The compressed/decompressed signal was then back-projected onto the sky using the PLANCK scanning strategy. The two maps were analyzed using the \texttt{anafast} Healpix procedure and both reconstructed [math]C_\ell[/math] were compared. The result is shown for a quantization step [math]Q=0.5[/math].

Effect of the PLANCK compression algorithm on the reconstructed power spectrum ([math]C_\ell[/math]) after data projection and map-making, according to the simulation. The upper plot shows the input reconstructed CMB power spectrum (black), the CMB+noise spectrum for this channel (blue, barely visible) and the reconstructed [math]C_\ell[/math]) when including the data compression in the chain (red). The lower plot shows these last two ratios and confirms the white nature of the final added noise at a level that can still be computed by the Quantization Theorem ([math]2\%[/math] for [math]Q=0.5[/math] used here).

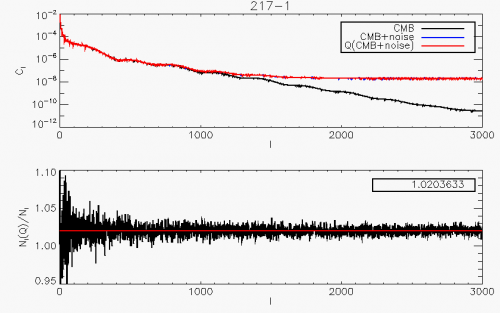
It is remarkable that the full procedure of baseline-subtraction+quantization+ring-making+map-making still leads to the [math]2\%[/math] increase of the variance that is predicted by the simple timeline quantization (for [math]Q/\sigma=2[/math]). Furthermore we check that the noise added by the compression algorithm is white.

It is not expected that the compression brings any non-gaussianity, since the pure quantization process does not add any skewness and less than 0.001 kurtosis, and coaddition of circles and then rings erases any non-gaussian contribution according to the Central Limit Theorem.

<biblio force=false>

1. References

</biblio>