Difference between revisions of "LFI-Validation"
| Line 27: | Line 27: | ||
File:PlanckFig_map_Diff070yr1+yr3-yr2+yr4sm3I_Stokes_88mm.png | File:PlanckFig_map_Diff070yr1+yr3-yr2+yr4sm3I_Stokes_88mm.png | ||
</gallery> | </gallery> | ||
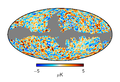
| − | '''Null map samples: top to bottom 30,44,70GHz; Left to right: ringhalf differences I, Q, 2 year combination differences I, Q. All maps smoothed to 3 degrees''' | + | '''Figure 1: Null map samples: top to bottom 30,44,70GHz; Left to right: ringhalf differences I, Q, 2 year combination differences I, Q. All maps smoothed to 3 degrees''' |
| Line 33: | Line 33: | ||
Three things are worth pointing out generally about these maps. | Three things are worth pointing out generally about these maps. | ||
First- there are no obvious 'features' standing out at this resolution and noise level. Earlier versions of the data processing, where there were errors in calibration for instance, would show scan-correlated structures at much larger amplitude. | First- there are no obvious 'features' standing out at this resolution and noise level. Earlier versions of the data processing, where there were errors in calibration for instance, would show scan-correlated structures at much larger amplitude. | ||
| − | Second- The half-ring difference maps and the2 year combination | + | Second- The half-ring difference maps and the2 year combination difference maps give a very similar overall impression. This is a very good sign, as these two typese of null cover very different time scales (1 hour to 2 years). |
| − | Third- Its impossible to know how 'good' the test is just by looking at the map. There is clearly noise, but determining if it is consistent with the noise model of the instrument, and further, if it will bias the scientific results, requires more | + | Third- Its impossible to know how 'good' the test is just by looking at the map. There is clearly noise, but determining if it is consistent with the noise model of the instrument, and further, if it will bias the scientific results, requires more analysis. |
===Statistical Analyses=== | ===Statistical Analyses=== | ||
The next level of data compression is to use the angular power spectra of the null tests, and to compare to simulations in a statistically robust way. We use two different approaches. | The next level of data compression is to use the angular power spectra of the null tests, and to compare to simulations in a statistically robust way. We use two different approaches. | ||
| Line 40: | Line 40: | ||
In the second, we use noise monte carlos from the FFP8 simulations, where we run the mapmaking identically to the real data, over data sets with identical sampling to the real data but consisting of noise only generated to match the per-detector LFI noise model. | In the second, we use noise monte carlos from the FFP8 simulations, where we run the mapmaking identically to the real data, over data sets with identical sampling to the real data but consisting of noise only generated to match the per-detector LFI noise model. | ||
| − | + | Here we show examples comparing the pseudospectra of a set of 100 monte carlos to the real data. We mask both data and simlations to concentrate on residuals impactin CMB analyses away from the galactic plane. | |
| − | + | ||
| + | [[File:null_cl_ffp8_070yr1+yr3-yr2+yr4_TT_lin_88mm.png|thumb|center|400px]] | ||
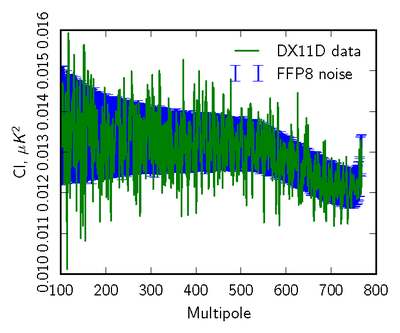
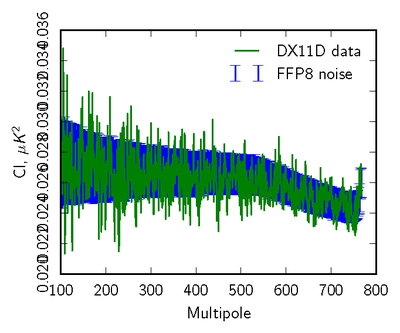
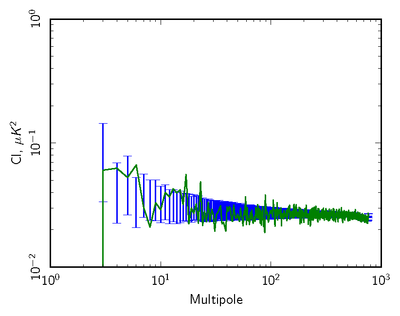
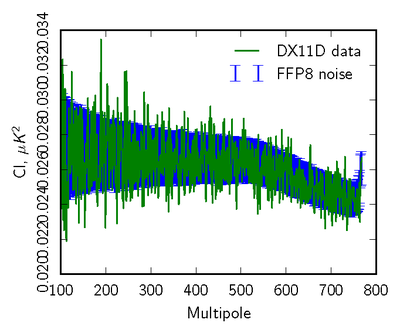
| + | [[File:null_cl_ffp8_070yr1+yr3-yr2+yr4_TT_log88mm.png|thumb|center|400px|'''Figure 2: Pseudospectrum comparison (70 GHz TT) of two year data difference(Year(1+3)-year(2+4)-green) to FFP8 simulation distribution(blue error bars)''']] | ||
| + | |||
| + | [[File:null_cl_ffp8_070yr1+yr3-yr2+yr4_EE_lin_88mm.png|thumb|center|400px]] | ||
| + | [[File:null_cl_ffp8_070yr1+yr3-yr2+yr4_EE_log88mm.png|thumb|center|400px|'''Figure 3: Pseudospectrum comparison (70 GHz EE) of two year data difference(Year(1+3)-year(2+4)-green) to FFP8 simulation distribution(blue error bars)''']] | ||
| + | [[File:null_cl_ffp8_070yr1+yr3-yr2+yr4_BB_lin_88mm.png|thumb|center|400px]] | ||
| + | [[File:null_cl_ffp8_070yr1+yr3-yr2+yr4_BB_log88mm.png|thumb|center|400px|'''Figure 4: Pseudospectrum comparison(70GHz BB) of two year data difference(Year(1+3)-year(2+4)-green) to FFP8 simulation distribution(blue error bars)''']] | ||
| − | |||
| − | |||
Finally, we can look at the distribution of noise power from the monte carlos 'ell by ell' and check where the real data fall in that distribution, to see if it is consistent with noise alone. | Finally, we can look at the distribution of noise power from the monte carlos 'ell by ell' and check where the real data fall in that distribution, to see if it is consistent with noise alone. | ||
| − | ( | + | |
| + | [[File:ffp8_dist_070full-survey_1survey_3_TT88mm_nt.png|350px|]] | ||
| + | [[File:ffp8_dist_070full-survey_1survey_3_EE88mm_nt.png|350px|]] | ||
| + | [[File:ffp8_dist_070full-survey_1survey_3_BB88mm_nt.png|350px|]] | ||
| + | |||
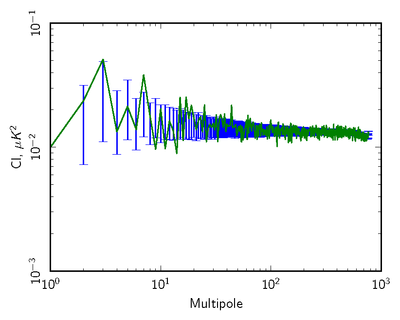
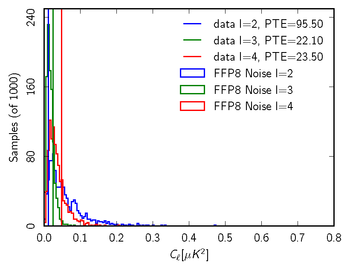
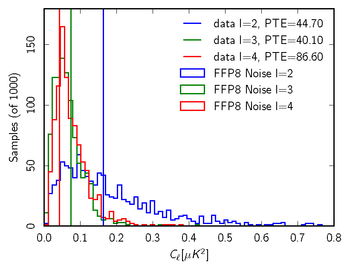
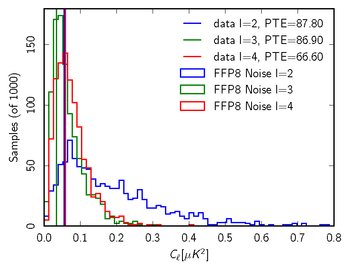
| + | '''Figure 5: Sample 70 GHz null test in comparison with FFP8 null distribution for l = 2-4. From left to right; TT,EE,BB. In this case, the null test is the full mission map - survey(1+3). We report the probability to exceed (PTE) values for the data relative to the distributions. All values for this example are very reasonable, suggesting our noise model captures the important features of the data.''' | ||
| + | |||
==Consistency checks == | ==Consistency checks == | ||
Revision as of 07:43, 5 February 2015
Contents
Overview[edit]
Data validation is critical at each step of the analysis pipeline. Much of the LFI data validation is based on null tests. Here we present some examples from the current release, with comments on relevant time scales and sensitivity to various systematics.
Null tests approach[edit]
Null tests at map level are performed routinely, whenever changes are made to the mapmaking pipeline. These include differences at survey, year, 2 year, half mission and ringhalf levels, for single detectors, horns, horn pairs and full frequency complements. Where possible, map differences are generated in I, Q and U. For this release, we use the Full Focal Plane 8 (FFP8) simulations for comparison. We can use FFP8 noise simulations, identical to the data in terms of sky sampling and with matching time domain noise characteristics, to make statistical arguments about the likelihood of the noise observed in the actual data nulls. In general null tests are performed in order to highlight possible issues in the data related to instrumental systematic effecst not properly accounted for within the processing pipeline, or related to known changes in the operational conditions (e.g. switch-over of the sorption coolers), or related to intrinsic instrument properties coupled with the sky signal, such as stray light contamination. Such null-tests can be performed using data on different time scales ranging from one minute to one year of observations, at different unit levels (radiometer, horn, horn-pair), within frequency and cross-frequency, both in total intensity, and, when applicable, in polarisation.
Sample Null Maps[edit]
Figure 1: Null map samples: top to bottom 30,44,70GHz; Left to right: ringhalf differences I, Q, 2 year combination differences I, Q. All maps smoothed to 3 degrees
Three things are worth pointing out generally about these maps. First- there are no obvious 'features' standing out at this resolution and noise level. Earlier versions of the data processing, where there were errors in calibration for instance, would show scan-correlated structures at much larger amplitude. Second- The half-ring difference maps and the2 year combination difference maps give a very similar overall impression. This is a very good sign, as these two typese of null cover very different time scales (1 hour to 2 years). Third- Its impossible to know how 'good' the test is just by looking at the map. There is clearly noise, but determining if it is consistent with the noise model of the instrument, and further, if it will bias the scientific results, requires more analysis.
Statistical Analyses[edit]
The next level of data compression is to use the angular power spectra of the null tests, and to compare to simulations in a statistically robust way. We use two different approaches. In the first we compare pseudospectra of the null maps to the half ring spectra, which are the most 'free' of anticipated systmatics. In the second, we use noise monte carlos from the FFP8 simulations, where we run the mapmaking identically to the real data, over data sets with identical sampling to the real data but consisting of noise only generated to match the per-detector LFI noise model.
Here we show examples comparing the pseudospectra of a set of 100 monte carlos to the real data. We mask both data and simlations to concentrate on residuals impactin CMB analyses away from the galactic plane.
Finally, we can look at the distribution of noise power from the monte carlos 'ell by ell' and check where the real data fall in that distribution, to see if it is consistent with noise alone.
Figure 5: Sample 70 GHz null test in comparison with FFP8 null distribution for l = 2-4. From left to right; TT,EE,BB. In this case, the null test is the full mission map - survey(1+3). We report the probability to exceed (PTE) values for the data relative to the distributions. All values for this example are very reasonable, suggesting our noise model captures the important features of the data.
Consistency checks[edit]
All the details can be found in Planck-2013-II[1]Planck-2015-A03[2].
Intra frequency consistency check[edit]
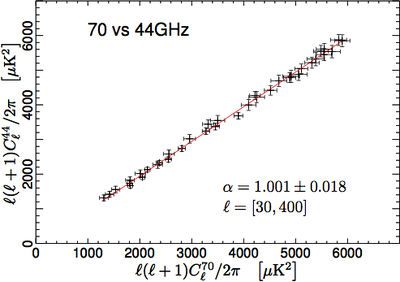
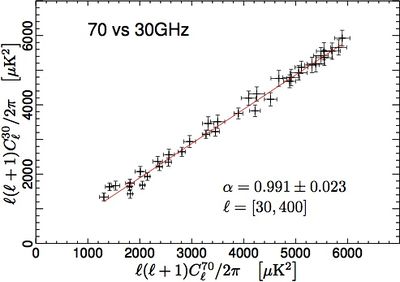
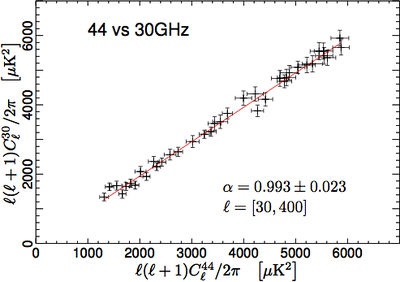
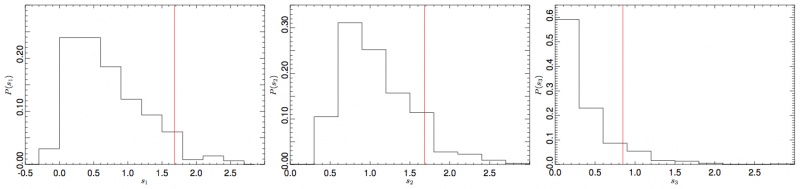
We have tested the consistency between 30, 44, and 70 GHz maps by comparing the power spectra in the multipole range around the first acoustic peak. In order to do so, we have removed the estimated contribution from unresolved point source from the spectra. We have then built the scatter plots for the three frequency pairs, i.e. 70 vs 30 GHz, 70 vs 44 GHz, and 44 vs 30 GHz, and performed a linear fit accounting for errors on both axis. The results reported in Fig. 1 show that the three power spectra are consistent within the errors. Moreover, please note that current error budget does not account for foreground removal, calibration, and window function uncertainties. Hence, the resulting agreement between spectra at different frequencies can be fairly considered even more significant.
70 GHz internal consistency check[edit]
We use the Hausman test [3] to assess the consistency of auto and cross spectral estimates at 70 GHz. We define the statistic:
where and represent auto- and cross-spectra respectively. In order to combine information from different multipoles into a single quantity, we define the following quantity:
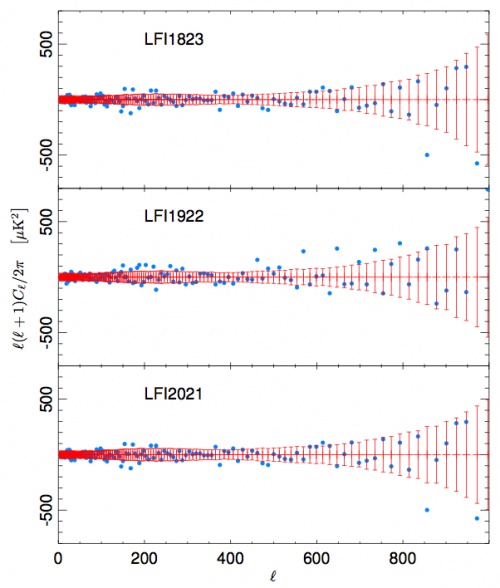
where denotes integer part. The distribution of converges (in a functional sense) to a Brownian motion process, which can be studied through the statistics and . Using the FFP7 simulations we derive the empirical distribution for all the three test statistics and we compare with results obtained from Planck data (see Fig. 2). Thus, the Hausman test shows no statistically significant inconsistencies between the two spectral estimates.
As a further test, we have estimated the temperature power spectrum for each of three horn-pair map, and we have compared the results with the spectrum obtained from all the 12 radiometers shown above. In Fig. 3 we show the difference between the horn-pair and the combined power spectra. Again, the error bars have been estimated from the FFP7 simulated dataset. A analysis of the residual shows that they are compatible with the null hypothesis, confirming the strong consistency of the estimates.
References[edit]
- ↑ Planck 2013 results. II. Low Frequency Instrument data processing, Planck Collaboration, 2014, A&A, 571, A2
- ↑ Planck 2015 results. II. LFI processing, Planck Collaboration, 2016, A&A, 594, A2.
- ↑ Unbiased estimation of an angular power spectrum, G. Polenta, D. Marinucci, A. Balbi, P. de Bernardis, E. Hivon, S. Masi, P. Natoli, N. Vittorio, J. Cosmology Astropart. Phys., 11, 1, (2005).
(Planck) Low Frequency Instrument
Cosmic Microwave background
[LFI meaning]: absolute calibration refers to the 0th order calibration for each channel, 1 single number, while the relative calibration refers to the component of the calibration that varies pointing period by pointing period.